人教版 七年级数学上册 4.3.3 《余角和补角》 课件(共34张PPT)
文档属性
| 名称 | 人教版 七年级数学上册 4.3.3 《余角和补角》 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览










文档简介
(共34张PPT)
第四章
几何图形初步
4.3.3
余角和补角
学习目标
1.了解余角、补角的概念.
2.掌握余角和补角的性质,能运用余角与补角的性质解决一些简单的实际问题.
3.通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.
4.方位角的定义与应用.
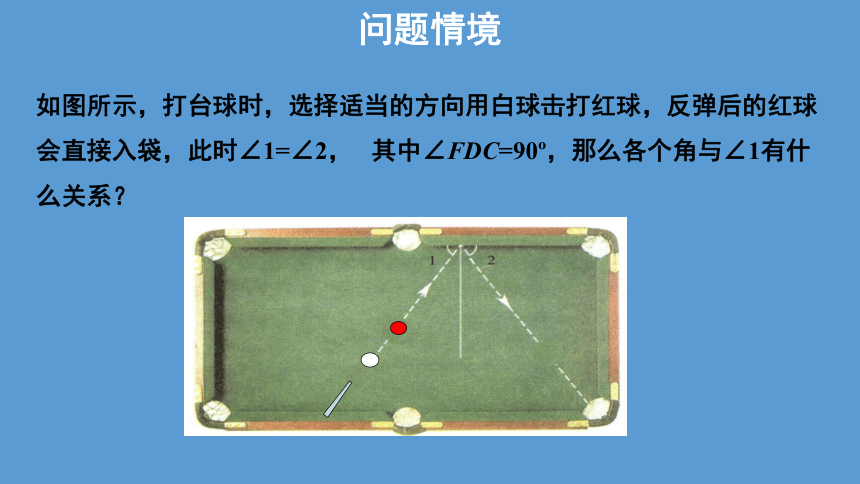
如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,
其中∠FDC=90?,那么各个角与∠1有什么关系?
问题情境
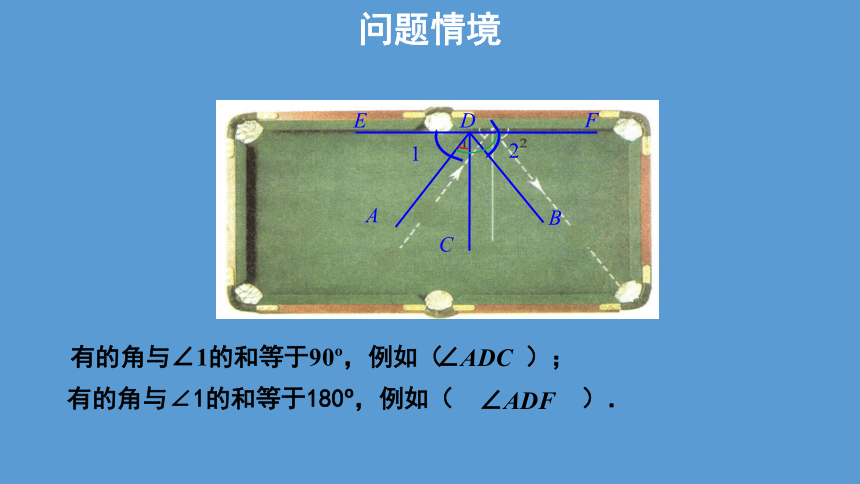
有的角与∠1的和等于90?,例如(
);
∠ADC
有的角与∠1的和等于180?,例如(
).
∠ADF
A
C
B
E
D
F
1
2
问题情境
在一副三角尺中,每块都有一个角是90°,而其他两个角的和是多少呢?
30°+60°=90°,45°+45°=90°.
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
探究新知
余角的定义
补角定义
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
即:若∠3+∠4=180°,那么∠3是∠4的补角,∠4也是∠3的补角.
定义中的“互为”是什么意思?
即每一个角都是另一个角的余角(补角).
探究新知
∠1与∠2,∠3都互为补角,∠2和∠3的大小有什么关系?
探究余角和补角的性质
因为∠1与∠2和∠3都互为补角,
所以∠2=180?-∠1,∠3=180?-∠1.
所以∠2=∠3.
探究新知
4
2
已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4
相等吗?为什么?
由∠1与∠2互补,得∠1+∠2=180?,所以
∠2=180?-∠1.
由∠3与∠4互补,得∠3+∠4=180?,所以∠4=180?-∠3.
又因为∠1=∠3,所以180?-∠1=180?-∠3,
所以∠2=∠4.
1
3
探究新知
探究新知
对于余角是否也有类似性质?
∠1与∠2,∠3都互为余角,∠2和∠3的大小有什么关系?
因为∠1与∠2和∠3都互为余角,
所以∠2=90?-∠1,∠3=90?-∠1.
所以∠2=∠3.
等角
的余角相等.
归纳:补角的性质:
等角
的补角相等.
余角的性质:
(同角)
(同角)
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线,并画出示意图吗?
可疑船
缉私艇
B
A
探究新知
探究新知
在航行、测绘等工作以及生活中,我们经常会碰到用方位角描述一个物体的方位,那么什么叫做方位角?如何用方位角描述方向呢?
方位角是表示方向的角,以正北、正南方向为基准来描述物体所处的方向,如北偏西30°,南偏东25°.
北
东
南
西
A
67°
北偏东67°
可疑船
缉私艇
B
A
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线吗?
画出示意图.
做一做: 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
60
°
北
西
南
东
O
A
探究新知
O
东
南
西
北
60°
射线OA的方向就是南偏东60°,即灯塔A所在的方向.
射线OB的方向就是北偏东40°,即客轮B所在的方向.
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
45°
A
B
D
C
探究新知
用方位角确定物体的画法步骤:
①先找出中心点,然后画出方向指标;
②把中心点和目的地用线连接起来;
③度量向北的射线和视线(中心点和目的地的连线)夹角.
探究新知
例1. 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为余角?
典型例题
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC
,∠BOC,
=90°.
所以,
∠COD
和∠COE互为余角,
同理,
∠AOD
和∠BOE,
∠AOD和∠COE
,
∠COD和∠BOE也互为余角.
所以∠COD
+∠COE=
∠AOC+
∠BOC
=
(∠AOC+
∠BOC)
典型例题
例2.图中给出的各角中,哪些互为余角?哪些互为补角?
10°与80°,30°与60°互为余角;
10°与170°,30°与150°,60°与120°,80°与100°互为补角.
典型例题
例3.
一个角是70°39′,求它的余角和补角.
解:它的余角是90°-70°39′=19°21′;
它的补角是180°-70°39′=109°21′.
例4.
∠α的补角是它的3倍,∠α是多少度?
解:由180°-
∠α=3
∠α,
解得∠α=45°.
典型例题
例5
.如果一个角的补角是这个角的余角的3倍,求这个角.
解:设这个角为x,则它的补角为180°-x,
它的余角为90°-x.于是就有
180°-x=3(90°-
x).
解得:x=45°.
典型例题
例
6.(1)如图,四条表示方向的射线中,表示北偏东30°的是(
)
D
典型例题
(2)如图所示,射线OA表示
方向,
射线OB表示
方向.
北偏西70°
南偏东15°
70°
B
15°
北
西
南
东
O
A
典型例题
课堂练习
1.已知∠α的补角是125°,则∠α的度数是(
).
A.55°
B.65°
C.75°
D.85°
2.下列说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的余角,那么它们相等;④锐角和钝角互补.其中,正确的说法有(
).
A.1个
B.2个
C.3个
D.4个
3.一个角为35°39′,则这个角的余角为________,补角为________.
A
B
54°21′
144°21′
课堂练习
4.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
解:设这个角的度数为x°,依题意,得:
180-x+24=5x.
解得:x=34.
所以这个角的度数是34°.
课堂练习
5.如图,E,D,F在同一直线上,∠CDE=90°,∠1=∠2.
(1)∠ADC与∠BDC有什么关系?为什么?
(2)∠ADF与∠BDE有什么关系?为什么?
解:(1)∠ADC=∠BDC.
理由:因为∠CDF=∠EDF-∠CDF=180°-90°=90°,
所以∠2+∠BDC=∠CDF=90°.
又因为∠1+∠ADC=∠CDE=90°,
且∠1=∠2,
所以∠ADC=∠BDC.
课堂练习
(2)∠ADF=∠BDE.
理由:因为∠ADF=180°-∠1,∠BDE=180°-∠2,
又因为∠1=∠2,
所以∠ADF=∠BDE.
课堂练习
6.如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?
互余
互补
相等
相等
课堂练习
7.(1)互余且相等的两个角,各是多少度?
(2)一个锐角的补角比这个角的余角大多少度?
45°
90°
8.如图,OA是表示北偏东30°方向的一条射线,仿照这条射线画出表示下列方向的射线:
(1)南偏东25°;
(2)北偏西60°.
解:如图所示,
OB表示南偏东25°,
OC表示北偏西60°.
C
B
25°
60°
30°
北
西
南
东
O
A
课堂练习
1.余角的定义:
一般地,如果两个角的和等于90°(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
2.补角的定义:
如果两个角的和等于180°(平角),就说这两个角互为补角,即其
中一个角是另一个角的补角.
3.余角与补角的性质:
同角(等角)的补角相等;
同角(等角)的余角相等.
4.方位角
课堂小结
课堂小结
本图片资源介绍了两角互余与互补的概念及余(补)角的性质,适用于余角和补角的教学.若需使用,请插入图片【知识点解析】互余与互补.
?
课堂小结
本图片资源讲解了方位角的概念及相关知识,加深了对方位角及相关知识的理解,适用于方位角的教学.若需使用,请插入图片【知识点解析】方位角.
?
再见
第四章
几何图形初步
4.3.3
余角和补角
学习目标
1.了解余角、补角的概念.
2.掌握余角和补角的性质,能运用余角与补角的性质解决一些简单的实际问题.
3.通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.
4.方位角的定义与应用.
如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,
其中∠FDC=90?,那么各个角与∠1有什么关系?
问题情境
有的角与∠1的和等于90?,例如(
);
∠ADC
有的角与∠1的和等于180?,例如(
).
∠ADF
A
C
B
E
D
F
1
2
问题情境
在一副三角尺中,每块都有一个角是90°,而其他两个角的和是多少呢?
30°+60°=90°,45°+45°=90°.
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
探究新知
余角的定义
补角定义
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
即:若∠3+∠4=180°,那么∠3是∠4的补角,∠4也是∠3的补角.
定义中的“互为”是什么意思?
即每一个角都是另一个角的余角(补角).
探究新知
∠1与∠2,∠3都互为补角,∠2和∠3的大小有什么关系?
探究余角和补角的性质
因为∠1与∠2和∠3都互为补角,
所以∠2=180?-∠1,∠3=180?-∠1.
所以∠2=∠3.
探究新知
4
2
已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4
相等吗?为什么?
由∠1与∠2互补,得∠1+∠2=180?,所以
∠2=180?-∠1.
由∠3与∠4互补,得∠3+∠4=180?,所以∠4=180?-∠3.
又因为∠1=∠3,所以180?-∠1=180?-∠3,
所以∠2=∠4.
1
3
探究新知
探究新知
对于余角是否也有类似性质?
∠1与∠2,∠3都互为余角,∠2和∠3的大小有什么关系?
因为∠1与∠2和∠3都互为余角,
所以∠2=90?-∠1,∠3=90?-∠1.
所以∠2=∠3.
等角
的余角相等.
归纳:补角的性质:
等角
的补角相等.
余角的性质:
(同角)
(同角)
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线,并画出示意图吗?
可疑船
缉私艇
B
A
探究新知
探究新知
在航行、测绘等工作以及生活中,我们经常会碰到用方位角描述一个物体的方位,那么什么叫做方位角?如何用方位角描述方向呢?
方位角是表示方向的角,以正北、正南方向为基准来描述物体所处的方向,如北偏西30°,南偏东25°.
北
东
南
西
A
67°
北偏东67°
可疑船
缉私艇
B
A
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线吗?
画出示意图.
做一做: 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
60
°
北
西
南
东
O
A
探究新知
O
东
南
西
北
60°
射线OA的方向就是南偏东60°,即灯塔A所在的方向.
射线OB的方向就是北偏东40°,即客轮B所在的方向.
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
45°
A
B
D
C
探究新知
用方位角确定物体的画法步骤:
①先找出中心点,然后画出方向指标;
②把中心点和目的地用线连接起来;
③度量向北的射线和视线(中心点和目的地的连线)夹角.
探究新知
例1. 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为余角?
典型例题
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC
,∠BOC,
=90°.
所以,
∠COD
和∠COE互为余角,
同理,
∠AOD
和∠BOE,
∠AOD和∠COE
,
∠COD和∠BOE也互为余角.
所以∠COD
+∠COE=
∠AOC+
∠BOC
=
(∠AOC+
∠BOC)
典型例题
例2.图中给出的各角中,哪些互为余角?哪些互为补角?
10°与80°,30°与60°互为余角;
10°与170°,30°与150°,60°与120°,80°与100°互为补角.
典型例题
例3.
一个角是70°39′,求它的余角和补角.
解:它的余角是90°-70°39′=19°21′;
它的补角是180°-70°39′=109°21′.
例4.
∠α的补角是它的3倍,∠α是多少度?
解:由180°-
∠α=3
∠α,
解得∠α=45°.
典型例题
例5
.如果一个角的补角是这个角的余角的3倍,求这个角.
解:设这个角为x,则它的补角为180°-x,
它的余角为90°-x.于是就有
180°-x=3(90°-
x).
解得:x=45°.
典型例题
例
6.(1)如图,四条表示方向的射线中,表示北偏东30°的是(
)
D
典型例题
(2)如图所示,射线OA表示
方向,
射线OB表示
方向.
北偏西70°
南偏东15°
70°
B
15°
北
西
南
东
O
A
典型例题
课堂练习
1.已知∠α的补角是125°,则∠α的度数是(
).
A.55°
B.65°
C.75°
D.85°
2.下列说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的余角,那么它们相等;④锐角和钝角互补.其中,正确的说法有(
).
A.1个
B.2个
C.3个
D.4个
3.一个角为35°39′,则这个角的余角为________,补角为________.
A
B
54°21′
144°21′
课堂练习
4.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
解:设这个角的度数为x°,依题意,得:
180-x+24=5x.
解得:x=34.
所以这个角的度数是34°.
课堂练习
5.如图,E,D,F在同一直线上,∠CDE=90°,∠1=∠2.
(1)∠ADC与∠BDC有什么关系?为什么?
(2)∠ADF与∠BDE有什么关系?为什么?
解:(1)∠ADC=∠BDC.
理由:因为∠CDF=∠EDF-∠CDF=180°-90°=90°,
所以∠2+∠BDC=∠CDF=90°.
又因为∠1+∠ADC=∠CDE=90°,
且∠1=∠2,
所以∠ADC=∠BDC.
课堂练习
(2)∠ADF=∠BDE.
理由:因为∠ADF=180°-∠1,∠BDE=180°-∠2,
又因为∠1=∠2,
所以∠ADF=∠BDE.
课堂练习
6.如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?
互余
互补
相等
相等
课堂练习
7.(1)互余且相等的两个角,各是多少度?
(2)一个锐角的补角比这个角的余角大多少度?
45°
90°
8.如图,OA是表示北偏东30°方向的一条射线,仿照这条射线画出表示下列方向的射线:
(1)南偏东25°;
(2)北偏西60°.
解:如图所示,
OB表示南偏东25°,
OC表示北偏西60°.
C
B
25°
60°
30°
北
西
南
东
O
A
课堂练习
1.余角的定义:
一般地,如果两个角的和等于90°(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
2.补角的定义:
如果两个角的和等于180°(平角),就说这两个角互为补角,即其
中一个角是另一个角的补角.
3.余角与补角的性质:
同角(等角)的补角相等;
同角(等角)的余角相等.
4.方位角
课堂小结
课堂小结
本图片资源介绍了两角互余与互补的概念及余(补)角的性质,适用于余角和补角的教学.若需使用,请插入图片【知识点解析】互余与互补.
?
课堂小结
本图片资源讲解了方位角的概念及相关知识,加深了对方位角及相关知识的理解,适用于方位角的教学.若需使用,请插入图片【知识点解析】方位角.
?
再见
