人教版数学八年级上册11.3.2多边形的内角和课件(共33张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2多边形的内角和课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
11.3.2多边形
内角和
练一练
1、填空题
(1)连接多边形(
)的线段,叫做多边形的对角线。
(2)多边形的任何(
)所在的直线,整个多边形都在这条直线的(
),这样的多边形叫做凸多边形
。
(3)各个角(
),各条边(
)的多边形,叫做正多边形。
(4)一个n边形有(
)条边,
(
)个顶点,
(
)个内角,
(
2
)个外角。
2、画出下列多边形的全部对角线
不相邻的两个顶点
一条边
同一侧
都相等
都相等
n
n
n
n
复习
由上述这些图形,你能找到哪些我们熟习的几何图形?
三角形
四边形
六边形
八边形
……..
三角形的内角和是180°,那么四边形的内角和是多少呢?五边形呢?你是如何得到这个结论的?
合作学习
B
A
C
D
E
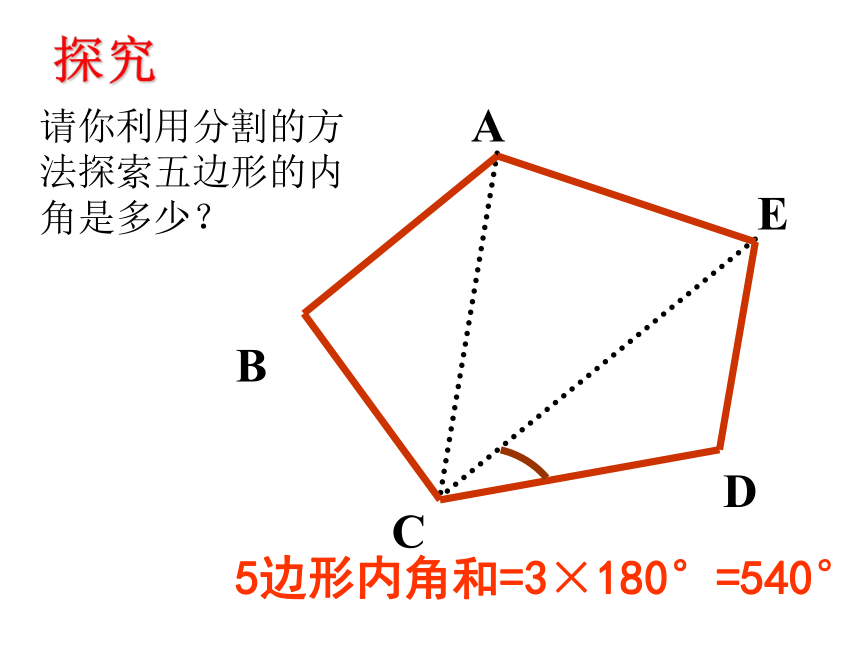
探究
5边形内角和=3×180°=540°
请你利用分割的方法探索五边形的内角是多少?
E
A
B
C
D
O
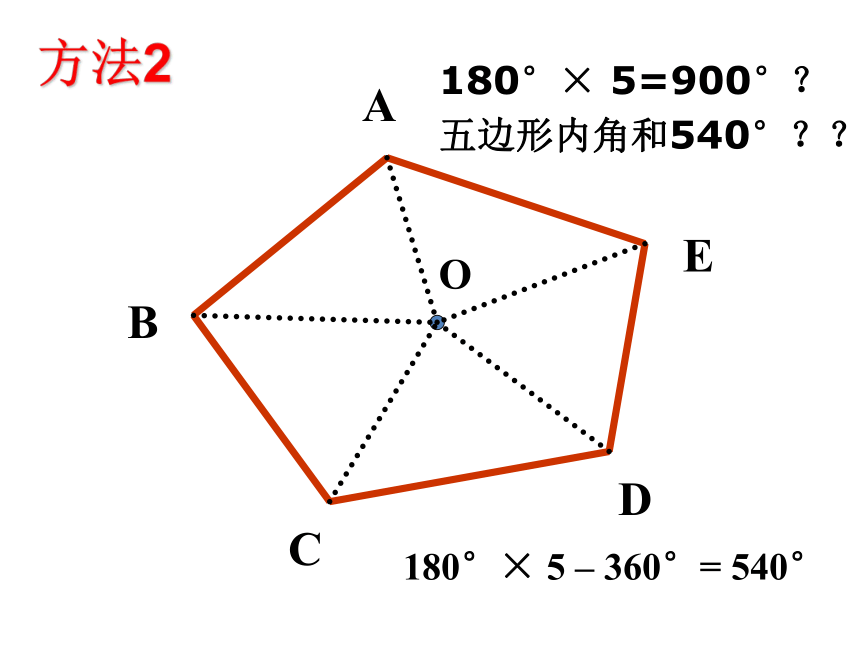
方法2
180°×
5
–
360°=
540°
180°×
5=900°?
五边形内角和540°??
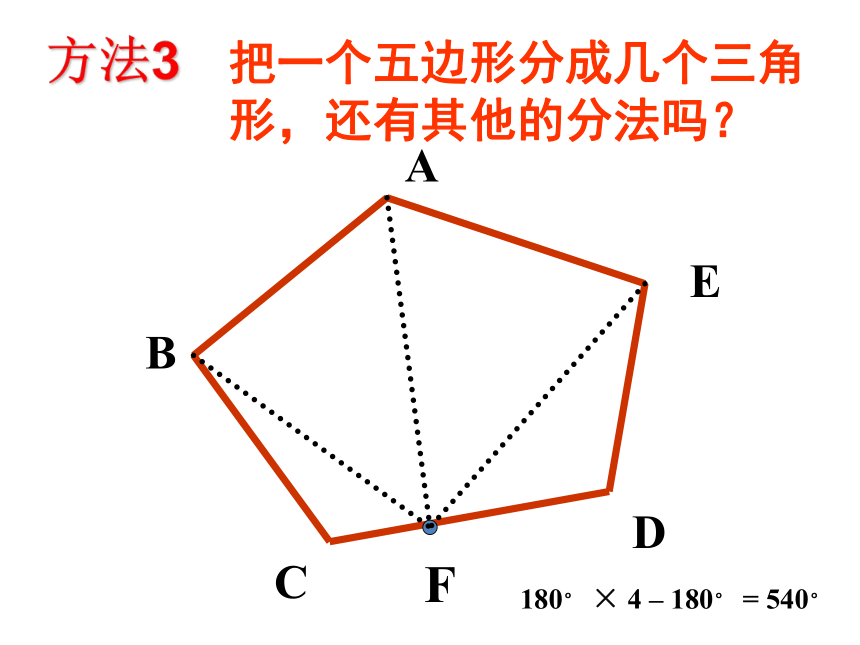
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°
×
4
–
180°
=
540°
方法3
选择同一种方法分别求出任意六边形、七边形、八边形的内角和等于多少度?
你能写出任意n边形的内角和吗?
从五边形的一个顶点出发,可以引(
)条对角线,他们将五边形分为多少个三角形,五边形的内角和等于180°×(
)。
从六边形的一个顶点出发,可以引(
)条对角线,他们将六边形分为多少个三角形,六边形的内角和等于180°×(
)。
从七边形的一个顶点出发,可以引(
)条对角线,他们将七边形分为多少个三角形,七边形的内角和等于180°×(
)。
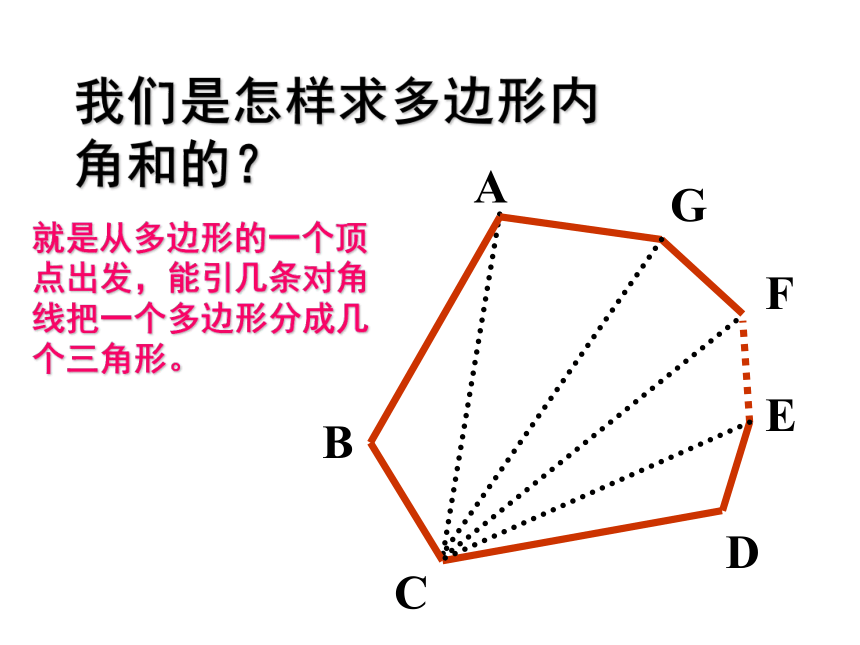
我们是怎样求多边形内
角和的?
B
A
C
D
G
F
E
就是从多边形的一个顶点出发,能引几条对角线把一个多边形分成几个三角形。
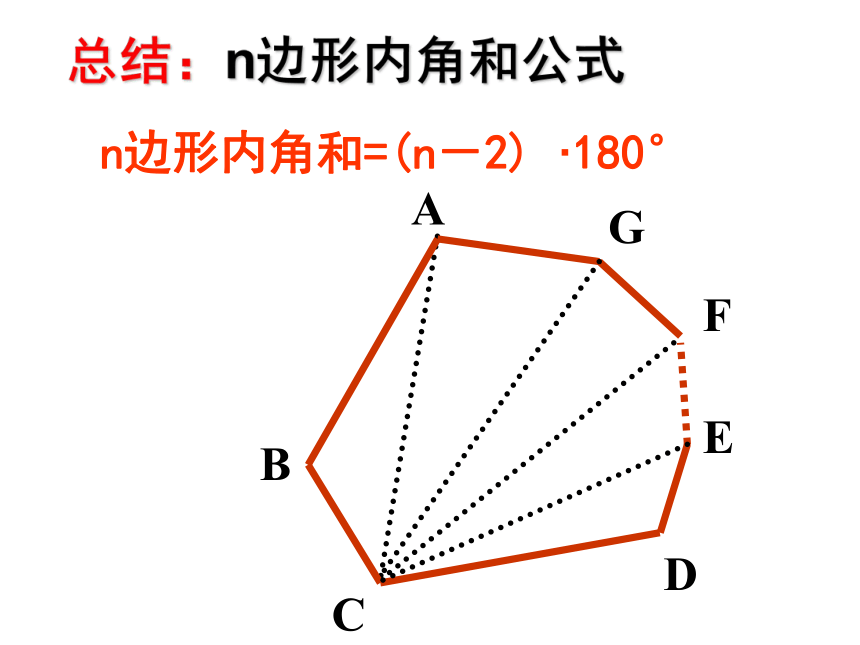
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
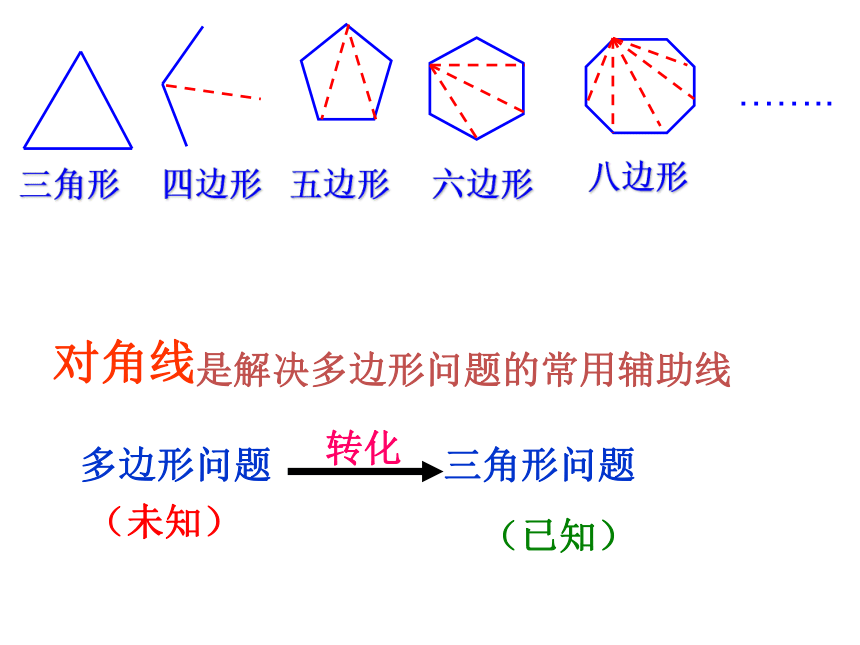
三角形
六边形
四边形
八边形
……..
五边形
是解决多边形问题的常用辅助线
对角线
多边形问题
三角形问题
转化
(未知)
(已知)
合作学习
请探索任意一个多边形的内角和与外角和的规律.
n边形
……
三角形
四边形
五边形
六边形
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
从上表中得到了什么结论?
结论:n边形的内角和为:
(n-2)×180°(n≥3).
n边形共有对角线
条(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
例1:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正
多边形的边数等于
360°÷30°=12。
练一练:
2、已知一个多边形的内角和为720o
,则这个多边形是______边形
6
3、在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
1、求十边形的内角和的度数。
解:(10-2)×180°=8
×180°=1440°
答:十边形的内角和是1440°
4、
过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.
5、填空(求边数)
(1)已知一个多边形的内角和为1080°,则它的边数为__。
(2)已知一个多边形的每一个内角都是156°,则它的边数为__。
8
15
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+(
y
-2)·180=1440
x
:
y=1
:
3
解之得
x
=3
y
=9
答:它们的边数分别是3和9。
例:
一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE,
CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两
直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E=
1/2
×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°=
720°
解:如图,在四边形ABCD中,
∠A+∠C=180°
∵∠A+∠B+∠C+∠D
=180°(4-2)=360°
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°=180°
例1:如果一个四边形的一组对角互补,那么另一组
对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
例2:如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.求六边形的外角和.
A
B
C
D
E
F
1
2
3
4
5
6
解:六边形的任何一个外角加上与它相邻的内角,都等于180°.因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和.
即外角和等于
6×180°-(6-2)×180°
=2×180°=360°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
多边形
图形
多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
合作学习
多边形的外角和
从上表中得到了什么结论?
结论:任何多边形的外角和为360°
(1)八边形的内角和为______,外角和为_____
1080°
360o
(2)已知一个多边形的每一个外角都是72o,求这个多边形的边数为______
5
A
B
C
D
E
F
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
1
2
P
Q
R
分析:如图所示:可向两个方向分别延长AB,CD,EF三条边,构成△PQR。
解:∵
DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,
∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF=
×720°=360°
例:
一个六边形如图,已知AB∥DE,BC∥EF
CD∥AF,求∠A+∠C+∠E的度数。
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
这节课你学到了什么?
还有什么困惑?
1.“二个一”(一个公式、一个性质)
2.
一种重要数学思想方法(转化思想)
谈一谈
小结:
是解决多边形问题的常用辅助线
对角线
多边形问题
三角形问题
转化
(未知)
(已知)
结论
n边形的内角和为(n-2)
×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线
条(n≥3)
任何多边形的外角和为360°
A
B
C
D
E
F
1.
一个六边形如图,已知
BA∥DE
,∠B=
∠
E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.
1
2
3
4
作业
2.巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
11.3.2多边形
内角和
练一练
1、填空题
(1)连接多边形(
)的线段,叫做多边形的对角线。
(2)多边形的任何(
)所在的直线,整个多边形都在这条直线的(
),这样的多边形叫做凸多边形
。
(3)各个角(
),各条边(
)的多边形,叫做正多边形。
(4)一个n边形有(
)条边,
(
)个顶点,
(
)个内角,
(
2
)个外角。
2、画出下列多边形的全部对角线
不相邻的两个顶点
一条边
同一侧
都相等
都相等
n
n
n
n
复习
由上述这些图形,你能找到哪些我们熟习的几何图形?
三角形
四边形
六边形
八边形
……..
三角形的内角和是180°,那么四边形的内角和是多少呢?五边形呢?你是如何得到这个结论的?
合作学习
B
A
C
D
E
探究
5边形内角和=3×180°=540°
请你利用分割的方法探索五边形的内角是多少?
E
A
B
C
D
O
方法2
180°×
5
–
360°=
540°
180°×
5=900°?
五边形内角和540°??
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180°
×
4
–
180°
=
540°
方法3
选择同一种方法分别求出任意六边形、七边形、八边形的内角和等于多少度?
你能写出任意n边形的内角和吗?
从五边形的一个顶点出发,可以引(
)条对角线,他们将五边形分为多少个三角形,五边形的内角和等于180°×(
)。
从六边形的一个顶点出发,可以引(
)条对角线,他们将六边形分为多少个三角形,六边形的内角和等于180°×(
)。
从七边形的一个顶点出发,可以引(
)条对角线,他们将七边形分为多少个三角形,七边形的内角和等于180°×(
)。
我们是怎样求多边形内
角和的?
B
A
C
D
G
F
E
就是从多边形的一个顶点出发,能引几条对角线把一个多边形分成几个三角形。
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2)
·180°
三角形
六边形
四边形
八边形
……..
五边形
是解决多边形问题的常用辅助线
对角线
多边形问题
三角形问题
转化
(未知)
(已知)
合作学习
请探索任意一个多边形的内角和与外角和的规律.
n边形
……
三角形
四边形
五边形
六边形
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2)
·180°
(n-2)
·180°
5
×180°
4
×180°
3
×180°
2
×180°
1
×180°
从上表中得到了什么结论?
结论:n边形的内角和为:
(n-2)×180°(n≥3).
n边形共有对角线
条(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
例1:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正
多边形的边数等于
360°÷30°=12。
练一练:
2、已知一个多边形的内角和为720o
,则这个多边形是______边形
6
3、在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
1、求十边形的内角和的度数。
解:(10-2)×180°=8
×180°=1440°
答:十边形的内角和是1440°
4、
过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.
5、填空(求边数)
(1)已知一个多边形的内角和为1080°,则它的边数为__。
(2)已知一个多边形的每一个内角都是156°,则它的边数为__。
8
15
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+(
y
-2)·180=1440
x
:
y=1
:
3
解之得
x
=3
y
=9
答:它们的边数分别是3和9。
例:
一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE,
CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两
直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E=
1/2
×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°=
720°
解:如图,在四边形ABCD中,
∠A+∠C=180°
∵∠A+∠B+∠C+∠D
=180°(4-2)=360°
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°=180°
例1:如果一个四边形的一组对角互补,那么另一组
对角有什么关系?
A
B
C
D
如果四边形的一组对角互补,那么另一组对角也互补.
例2:如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.求六边形的外角和.
A
B
C
D
E
F
1
2
3
4
5
6
解:六边形的任何一个外角加上与它相邻的内角,都等于180°.因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°.
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和.
即外角和等于
6×180°-(6-2)×180°
=2×180°=360°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
多边形
图形
多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
合作学习
多边形的外角和
从上表中得到了什么结论?
结论:任何多边形的外角和为360°
(1)八边形的内角和为______,外角和为_____
1080°
360o
(2)已知一个多边形的每一个外角都是72o,求这个多边形的边数为______
5
A
B
C
D
E
F
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
1
2
P
Q
R
分析:如图所示:可向两个方向分别延长AB,CD,EF三条边,构成△PQR。
解:∵
DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,
∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF=
×720°=360°
例:
一个六边形如图,已知AB∥DE,BC∥EF
CD∥AF,求∠A+∠C+∠E的度数。
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
这节课你学到了什么?
还有什么困惑?
1.“二个一”(一个公式、一个性质)
2.
一种重要数学思想方法(转化思想)
谈一谈
小结:
是解决多边形问题的常用辅助线
对角线
多边形问题
三角形问题
转化
(未知)
(已知)
结论
n边形的内角和为(n-2)
×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线
条(n≥3)
任何多边形的外角和为360°
A
B
C
D
E
F
1.
一个六边形如图,已知
BA∥DE
,∠B=
∠
E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.
1
2
3
4
作业
2.巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
