苏科版数学九年级上册2.3确定圆的条件课件(共16张PPT)
文档属性
| 名称 | 苏科版数学九年级上册2.3确定圆的条件课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
确定圆的条件
九年级苏教版数学上册
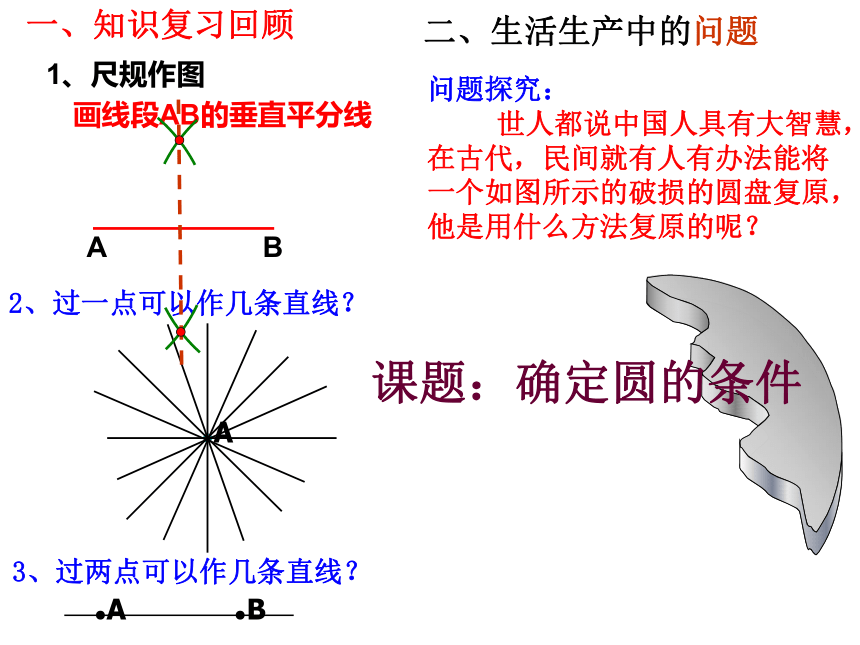
1、尺规作图
A
B
画线段AB的垂直平分线
一、知识复习回顾
2、过一点可以作几条直线?
3、过两点可以作几条直线?
●A
●A
●B
二、生活生产中的问题
问题探究:
世人都说中国人具有大智慧,在古代,民间就有人有办法能将一个如图所示的破损的圆盘复原,他是用什么方法复原的呢?
课题:确定圆的条件
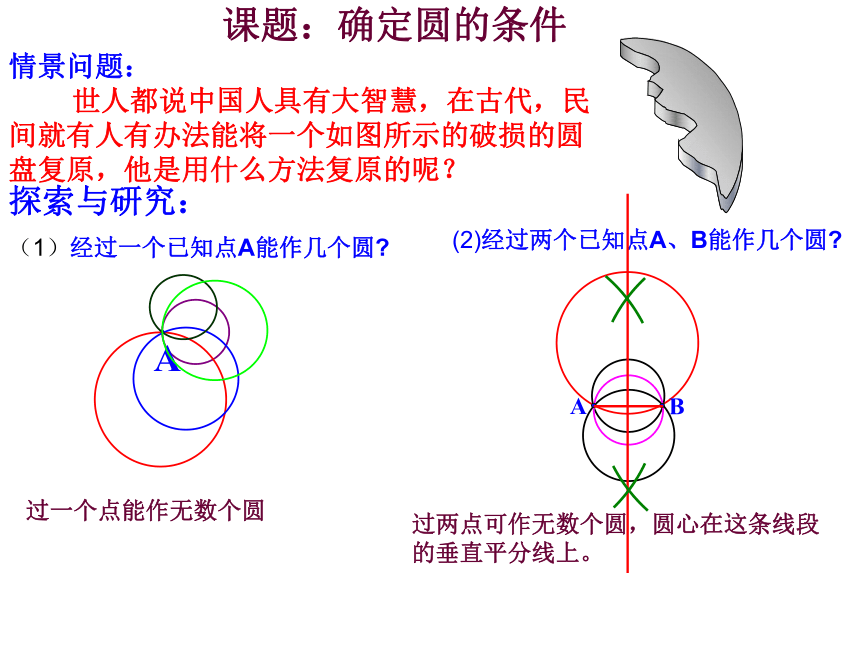
情景问题:
世人都说中国人具有大智慧,在古代,民间就有人有办法能将一个如图所示的破损的圆盘复原,他是用什么方法复原的呢?
课题:确定圆的条件
探索与研究:
(1)经过一个已知点A能作几个圆?
(2)经过两个已知点A、B能作几个圆?
过一个点能作无数个圆
过两点可作无数个圆,圆心在这条线段的垂直平分线上。
A
A
B
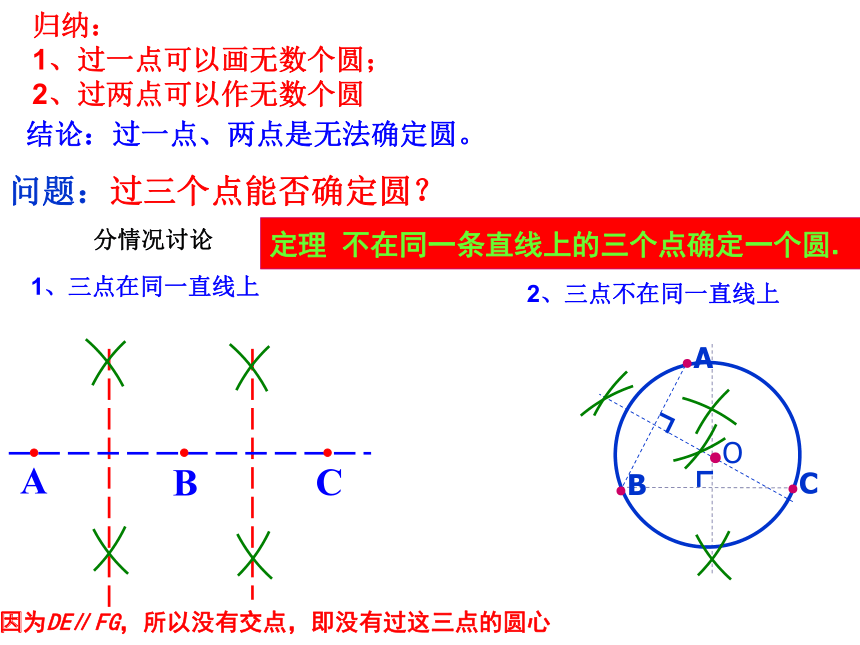
问题:过三个点能否确定圆?
归纳:
1、过一点可以画无数个圆;
2、过两点可以作无数个圆
结论:过一点、两点是无法确定圆。
┓
┏
●O
分情况讨论
A
B
C
●B
●C
●A
1、三点在同一直线上
2、三点不在同一直线上
因为DE∥FG,所以没有交点,即没有过这三点的圆心
定理
不在同一条直线上的三个点确定一个圆.
只要有不在同一条直线上的三点,就可以确定一个圆。
定理
不在同一条直线上的三个点确定一个圆.
问题解密
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
A
B
C
O
方法:
1、在圆弧上任取三点A、B、C。
并连接
⊙O即为所求。
2、定圆心
分别作两条线段的垂直平分线,
其交点O即为圆心。
3、定半径,并作圆
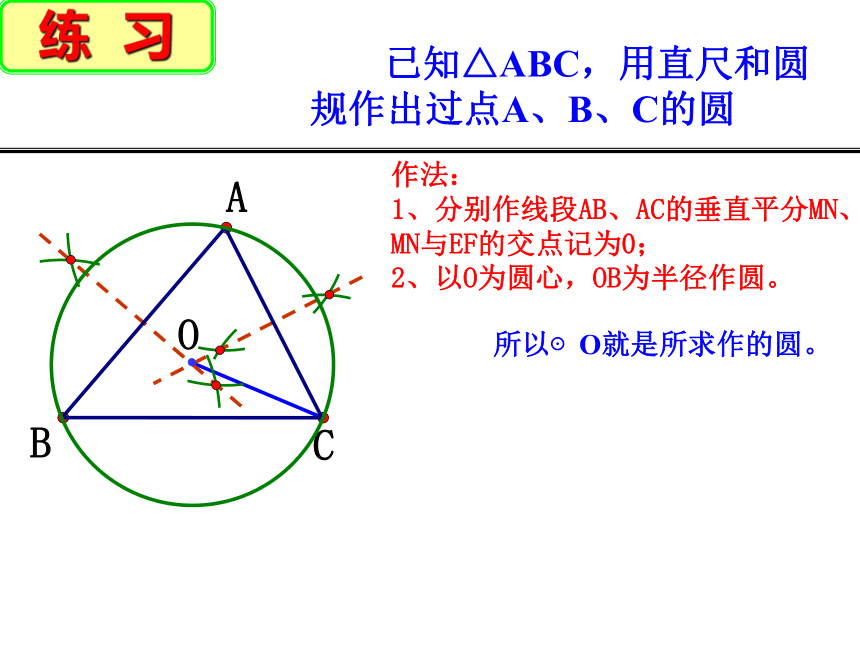
已知△ABC,用直尺和圆规作出过点A、B、C的圆
练
习
作图步骤:
1、确定圆心
2、确定半径,并画圆
3、下结论
A
B
C
O
已知△ABC,用直尺和圆规作出过点A、B、C的圆
练
习
作法:
1、分别作线段AB、AC的垂直平分MN、EF,MN与EF的交点记为0;
2、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
A
B
C
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
定
义
三角形的外心
三角形的外接圆
圆的内接三角形
A
B
C
O
性质归纳:
1、三角形的外心是△ABC
的交点,
它到三角形的
的距离相等。
三条边的垂直平分线
三个顶点
2、一个三角形有
个外接圆,一个圆有
个内接三角形。
一
无数
练习:
1.如图,△ABC是⊙O的
三角形,
⊙O是△ABC的
圆.
2.三角形的外心是三条边
的
交点.
3.判断题:
(1)经过三点可以确定一个圆.
(2)任意一个三角形都有一个外接圆,并且只
有一个.
(3)到三角形三个顶点距离相等的点是这个
三角形的外接圆的圆心.
内接
外接
垂直平分线
O
B
C
A
×
√
√
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
(图一)
(图二)
(图三)
锐角三角形的外心位于三角形
.
直角三角形的外心位于直角三角形
.
钝角三角形的外心位于三角形
.
1、比较这三个三角形外心的位置,你有何发现?
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
内
斜边的中点
外
(1)若三角形的外心在其内部,则该三角形是
(
)
A.任意三角形
B.直角三角形
C.钝角三角形
D.锐角三角形
(2)△ABC三边长分别是6,8,10时,
△ABC的外接圆的半径是
.
D
5
巩固练习:
变式:Rt△ABC两边长分别是6,8,则△ABC的外接圆的半径是
.
5或4
1、已知:等腰三角形ABC中,腰AB=13cm,底BC=10cm,求三角形ABC的外接圆的半径.
连结OB.设OB=xcm.
则在Rt△OBD中:
OB=x,BD=5,OD=12-x
∴52+(12-x)2=x2
……
O
D
A
B
C
10cm
x
x
12-x
5
13
分析:过A作AD⊥BC,垂足为D.
设O为外心,
则必在AD上,
A
B
C
2、已知:等腰三角形ABC中,腰AB=13cm
底BC=24cm,求三角形ABC的外接圆的半径.
D
O
x
12
x-5
(3)已知:A、B、C三点,根据下列条件,说明经过
A、B、C三点能否确定一个圆,若能,求出圆
的半径;若不能,请说明理由.
①
②
AB=5cm,BC=3cm,AC=4cm.
(4)
平面直角坐标系中,已知点A、B、C的坐标分别为
(1,—1)、(—2,5)、(4,—6)。试判断过点A、B、C这三点能否确定一个圆,并说明理由,
课堂小结
1、通过本课的学习,你有什么收获?还有什么问题?
2、确定圆的条件——
不在同一直线上的三点
圆心、半径
3、锐角三角形
在三角形的内部
直角三角形
--外心的位置---
在斜边上
钝角三角形
在三角形的外部
课后作业:
1、完成补充习题
2.3确定圆的条件
2、预习下节课内容,搜集现实生活中的
直线和圆的位置关系的现象。
能力提高
一地板上由于受到损坏,在地板上留下三个小洞A,B,C,
如图你准备用一块半径r为的圆形木板去遮住这三个小洞
①若AC=3cm,BC=4cm,AB=5cm,问半径
至少多少时,可以遮住这个洞?
②若∠ACB=60°,AB=6cm,
∠ABC,
∠BAC
均为锐角,问半径至少多少时,可以遮住这个洞?
③若∠ACB=120°,AB=8cm,
问半径至少多少时,可以遮住这个洞?
C
B
A
C
A
B
锐角三角形(和直角三角形)的最小覆盖圆是其外接圆
钝角三角形的最小覆盖圆是以其最长边为直径的圆。
结论:
A
B
用半径为r的圆形纸板去遮住A、B两个小洞
则圆的半径至少多少?
6cm
确定圆的条件
九年级苏教版数学上册
1、尺规作图
A
B
画线段AB的垂直平分线
一、知识复习回顾
2、过一点可以作几条直线?
3、过两点可以作几条直线?
●A
●A
●B
二、生活生产中的问题
问题探究:
世人都说中国人具有大智慧,在古代,民间就有人有办法能将一个如图所示的破损的圆盘复原,他是用什么方法复原的呢?
课题:确定圆的条件
情景问题:
世人都说中国人具有大智慧,在古代,民间就有人有办法能将一个如图所示的破损的圆盘复原,他是用什么方法复原的呢?
课题:确定圆的条件
探索与研究:
(1)经过一个已知点A能作几个圆?
(2)经过两个已知点A、B能作几个圆?
过一个点能作无数个圆
过两点可作无数个圆,圆心在这条线段的垂直平分线上。
A
A
B
问题:过三个点能否确定圆?
归纳:
1、过一点可以画无数个圆;
2、过两点可以作无数个圆
结论:过一点、两点是无法确定圆。
┓
┏
●O
分情况讨论
A
B
C
●B
●C
●A
1、三点在同一直线上
2、三点不在同一直线上
因为DE∥FG,所以没有交点,即没有过这三点的圆心
定理
不在同一条直线上的三个点确定一个圆.
只要有不在同一条直线上的三点,就可以确定一个圆。
定理
不在同一条直线上的三个点确定一个圆.
问题解密
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
A
B
C
O
方法:
1、在圆弧上任取三点A、B、C。
并连接
⊙O即为所求。
2、定圆心
分别作两条线段的垂直平分线,
其交点O即为圆心。
3、定半径,并作圆
已知△ABC,用直尺和圆规作出过点A、B、C的圆
练
习
作图步骤:
1、确定圆心
2、确定半径,并画圆
3、下结论
A
B
C
O
已知△ABC,用直尺和圆规作出过点A、B、C的圆
练
习
作法:
1、分别作线段AB、AC的垂直平分MN、EF,MN与EF的交点记为0;
2、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
A
B
C
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
定
义
三角形的外心
三角形的外接圆
圆的内接三角形
A
B
C
O
性质归纳:
1、三角形的外心是△ABC
的交点,
它到三角形的
的距离相等。
三条边的垂直平分线
三个顶点
2、一个三角形有
个外接圆,一个圆有
个内接三角形。
一
无数
练习:
1.如图,△ABC是⊙O的
三角形,
⊙O是△ABC的
圆.
2.三角形的外心是三条边
的
交点.
3.判断题:
(1)经过三点可以确定一个圆.
(2)任意一个三角形都有一个外接圆,并且只
有一个.
(3)到三角形三个顶点距离相等的点是这个
三角形的外接圆的圆心.
内接
外接
垂直平分线
O
B
C
A
×
√
√
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
(图一)
(图二)
(图三)
锐角三角形的外心位于三角形
.
直角三角形的外心位于直角三角形
.
钝角三角形的外心位于三角形
.
1、比较这三个三角形外心的位置,你有何发现?
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
内
斜边的中点
外
(1)若三角形的外心在其内部,则该三角形是
(
)
A.任意三角形
B.直角三角形
C.钝角三角形
D.锐角三角形
(2)△ABC三边长分别是6,8,10时,
△ABC的外接圆的半径是
.
D
5
巩固练习:
变式:Rt△ABC两边长分别是6,8,则△ABC的外接圆的半径是
.
5或4
1、已知:等腰三角形ABC中,腰AB=13cm,底BC=10cm,求三角形ABC的外接圆的半径.
连结OB.设OB=xcm.
则在Rt△OBD中:
OB=x,BD=5,OD=12-x
∴52+(12-x)2=x2
……
O
D
A
B
C
10cm
x
x
12-x
5
13
分析:过A作AD⊥BC,垂足为D.
设O为外心,
则必在AD上,
A
B
C
2、已知:等腰三角形ABC中,腰AB=13cm
底BC=24cm,求三角形ABC的外接圆的半径.
D
O
x
12
x-5
(3)已知:A、B、C三点,根据下列条件,说明经过
A、B、C三点能否确定一个圆,若能,求出圆
的半径;若不能,请说明理由.
①
②
AB=5cm,BC=3cm,AC=4cm.
(4)
平面直角坐标系中,已知点A、B、C的坐标分别为
(1,—1)、(—2,5)、(4,—6)。试判断过点A、B、C这三点能否确定一个圆,并说明理由,
课堂小结
1、通过本课的学习,你有什么收获?还有什么问题?
2、确定圆的条件——
不在同一直线上的三点
圆心、半径
3、锐角三角形
在三角形的内部
直角三角形
--外心的位置---
在斜边上
钝角三角形
在三角形的外部
课后作业:
1、完成补充习题
2.3确定圆的条件
2、预习下节课内容,搜集现实生活中的
直线和圆的位置关系的现象。
能力提高
一地板上由于受到损坏,在地板上留下三个小洞A,B,C,
如图你准备用一块半径r为的圆形木板去遮住这三个小洞
①若AC=3cm,BC=4cm,AB=5cm,问半径
至少多少时,可以遮住这个洞?
②若∠ACB=60°,AB=6cm,
∠ABC,
∠BAC
均为锐角,问半径至少多少时,可以遮住这个洞?
③若∠ACB=120°,AB=8cm,
问半径至少多少时,可以遮住这个洞?
C
B
A
C
A
B
锐角三角形(和直角三角形)的最小覆盖圆是其外接圆
钝角三角形的最小覆盖圆是以其最长边为直径的圆。
结论:
A
B
用半径为r的圆形纸板去遮住A、B两个小洞
则圆的半径至少多少?
6cm
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
