双曲线的标准方程
图片预览




文档简介
(共17张PPT)
*
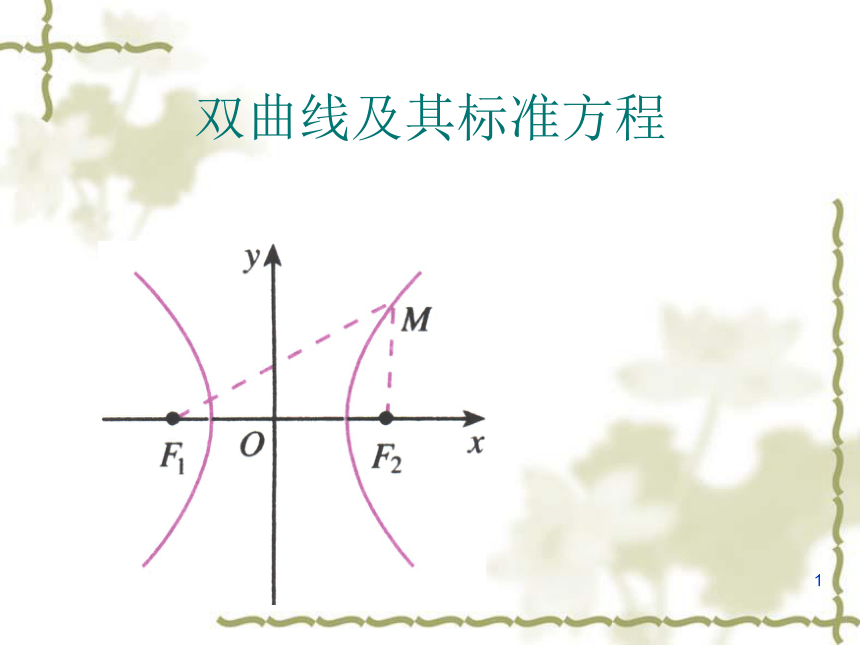
双曲线及其标准方程
*
回顾
1、椭圆的定义是什么?
2、椭圆的标准方程、焦点坐标是什么?
*
定义
图像
方程
焦点
a.b.c的关系
·
o
F1
F2
·
y
x
·
x
y
o
F1
F2
·
·
|MF1|+|MF2|=2a(2a>|F1F2|)
a2=b2+c2
F ( ±c,0) F(0, ± c)
*
那么与两定点的距离之差为常数的点的轨迹是怎样的曲线?
问题
与两定点 的距离之和为常数2a(2a>2c)
的点的轨迹是椭圆.
*
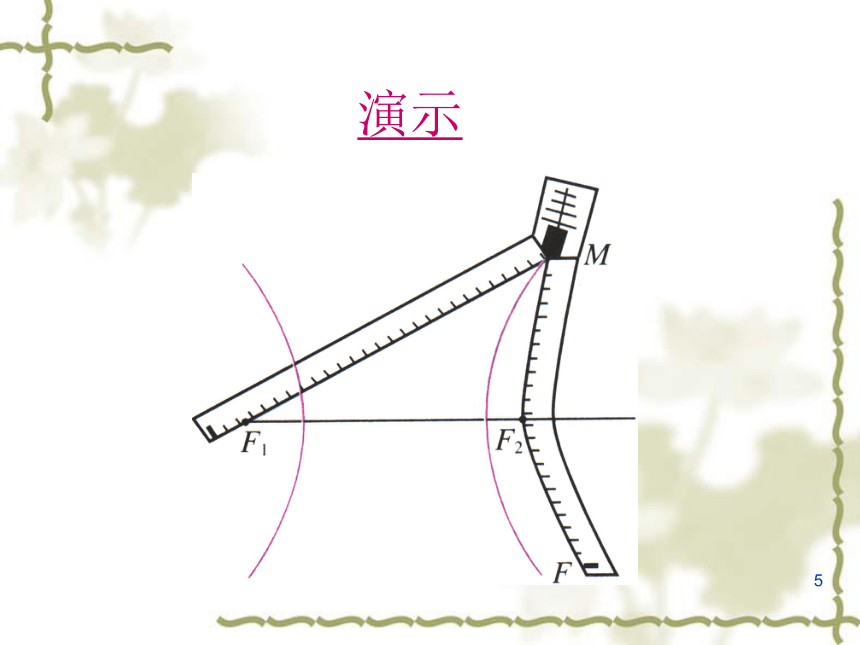
演示
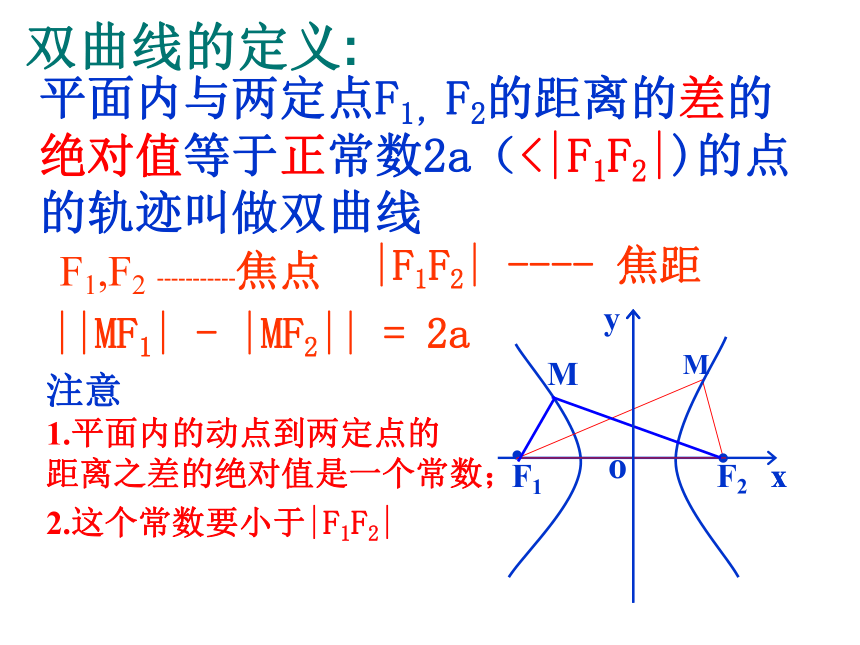
双曲线的定义:
F1,F2 -----------焦点
||MF1| - |MF2|| = 2a
|F1F2| ---- 焦距
.
F2
.
F1
M
y
o
x
注意
1.平面内的动点到两定点的
距离之差的绝对值是一个常数;
2.这个常数要小于|F1F2|
M
平面内与两定点F1,F2的距离的差的绝对值等于正常数2a(<|F1F2|)的点的轨迹叫做双曲线
x
*
思考
3、平面内与两定点的距离之差的绝对值等于常数2a
(2a>|F1F2|)的点的轨迹是什么?
2、平面内与两定点的距离之差的绝对值等于常数2a (2a=|F1F2| )的点的轨迹是什么?
1、平面内与两定点的距离之差等于常数2a(2a<|F1F2| )的点的轨迹是什么?
双曲线的一支
在直线F1F2上且 以F1、F2为端点向外的两条射线
不存在
4、平面内与两定点的距离之差的绝对值等于常数2a
(2a=0 )的点的轨迹是什么?
线段F1F2的垂直平分线
*
2.设点
1. 建系
3.列式
4.化简
双曲线的标准方程
*
将上述方程化为:
化简过程:
整理得:
由双曲线定义知:
即:
设
代入上式整理得:
*
( c2=a2+b2)
双曲线的标准方程
*
焦点在y轴上的双曲线的图象是什么样的?
标准方程是什么?
思考
注: x2与y2的系数的符号,决定焦点所在的坐标轴,当x2,y2哪个系数为正,焦点就在哪个轴上,双曲线的焦点所在位置与分母的大小无关。
*
例1、已知双曲线的焦点为 ,双曲线上一点到焦点的距离差的绝对值等于4,则
(1) a=____, c =____ , b =_____
(2) 双曲线的标准方程为________
(3)双曲线上一点P, |PF1|=10,
则|PF2|=_________
4或16
6
2
3
*
例2:k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
A、焦点在x轴上的椭圆
B、焦点在y轴上的双曲线
C、焦点在y轴上的椭圆
D、焦点在x轴上的双曲线
解:原方程化为:
∴方程的曲线为焦点在y轴上的双曲线。
B
*
例3、在相距2000米的两个观察站A、B先后听到远处传来的爆炸声,已知A站听到的时间比B站早4秒,声速是340米/秒,判断爆炸点可能分布在什么样的曲线上,并求出该曲线的方程。
解:设爆炸点为P,由题设知
,所以点 P 分布在以 A、B 为焦点的双曲线
且靠近A处的一支上。
y
x
o
.
.P
.
B
如图,以米为单位,建立直角坐标系,
得到
所以点P所在的曲线方程为
*
课堂练习
1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
D
2、若椭圆 与双曲线
的焦点相同,则 a=
3
*
( 为定点, 为常数)
小结
双曲线定义
图形
标准方程
焦点坐标
关系
*
课后作业:
1.求适合下列条件的双曲线的标准方程.
(1)
(2)焦点(0,-6),(0,6),经过点(2,-5).
3.已知方程 表示双曲线,求的取值范围.
2.已知方程 ,求
它的焦点坐标.
2.已知方程 ,求
它的焦点坐标.
2.已知方程 ,求
它的焦点坐标.
*
双曲线及其标准方程
*
回顾
1、椭圆的定义是什么?
2、椭圆的标准方程、焦点坐标是什么?
*
定义
图像
方程
焦点
a.b.c的关系
·
o
F1
F2
·
y
x
·
x
y
o
F1
F2
·
·
|MF1|+|MF2|=2a(2a>|F1F2|)
a2=b2+c2
F ( ±c,0) F(0, ± c)
*
那么与两定点的距离之差为常数的点的轨迹是怎样的曲线?
问题
与两定点 的距离之和为常数2a(2a>2c)
的点的轨迹是椭圆.
*
演示
双曲线的定义:
F1,F2 -----------焦点
||MF1| - |MF2|| = 2a
|F1F2| ---- 焦距
.
F2
.
F1
M
y
o
x
注意
1.平面内的动点到两定点的
距离之差的绝对值是一个常数;
2.这个常数要小于|F1F2|
M
平面内与两定点F1,F2的距离的差的绝对值等于正常数2a(<|F1F2|)的点的轨迹叫做双曲线
x
*
思考
3、平面内与两定点的距离之差的绝对值等于常数2a
(2a>|F1F2|)的点的轨迹是什么?
2、平面内与两定点的距离之差的绝对值等于常数2a (2a=|F1F2| )的点的轨迹是什么?
1、平面内与两定点的距离之差等于常数2a(2a<|F1F2| )的点的轨迹是什么?
双曲线的一支
在直线F1F2上且 以F1、F2为端点向外的两条射线
不存在
4、平面内与两定点的距离之差的绝对值等于常数2a
(2a=0 )的点的轨迹是什么?
线段F1F2的垂直平分线
*
2.设点
1. 建系
3.列式
4.化简
双曲线的标准方程
*
将上述方程化为:
化简过程:
整理得:
由双曲线定义知:
即:
设
代入上式整理得:
*
( c2=a2+b2)
双曲线的标准方程
*
焦点在y轴上的双曲线的图象是什么样的?
标准方程是什么?
思考
注: x2与y2的系数的符号,决定焦点所在的坐标轴,当x2,y2哪个系数为正,焦点就在哪个轴上,双曲线的焦点所在位置与分母的大小无关。
*
例1、已知双曲线的焦点为 ,双曲线上一点到焦点的距离差的绝对值等于4,则
(1) a=____, c =____ , b =_____
(2) 双曲线的标准方程为________
(3)双曲线上一点P, |PF1|=10,
则|PF2|=_________
4或16
6
2
3
*
例2:k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
A、焦点在x轴上的椭圆
B、焦点在y轴上的双曲线
C、焦点在y轴上的椭圆
D、焦点在x轴上的双曲线
解:原方程化为:
∴方程的曲线为焦点在y轴上的双曲线。
B
*
例3、在相距2000米的两个观察站A、B先后听到远处传来的爆炸声,已知A站听到的时间比B站早4秒,声速是340米/秒,判断爆炸点可能分布在什么样的曲线上,并求出该曲线的方程。
解:设爆炸点为P,由题设知
,所以点 P 分布在以 A、B 为焦点的双曲线
且靠近A处的一支上。
y
x
o
.
.P
.
B
如图,以米为单位,建立直角坐标系,
得到
所以点P所在的曲线方程为
*
课堂练习
1、已知点F1(- 8, 3 )、F2(2 ,3),动点P满足
|PF1| - |PF2|= 10,则P点的轨迹是( )
A、双曲线 B、双曲线一支
C、直线 D、一条射线
D
2、若椭圆 与双曲线
的焦点相同,则 a=
3
*
( 为定点, 为常数)
小结
双曲线定义
图形
标准方程
焦点坐标
关系
*
课后作业:
1.求适合下列条件的双曲线的标准方程.
(1)
(2)焦点(0,-6),(0,6),经过点(2,-5).
3.已知方程 表示双曲线,求的取值范围.
2.已知方程 ,求
它的焦点坐标.
2.已知方程 ,求
它的焦点坐标.
2.已知方程 ,求
它的焦点坐标.
