华东师大版七年级数学上册 第5章相交线与平行线检测题(word版含答案)
文档属性
| 名称 | 华东师大版七年级数学上册 第5章相交线与平行线检测题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 563.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-13 19:27:49 | ||
图片预览



文档简介
检测内容:相交线与平行线
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
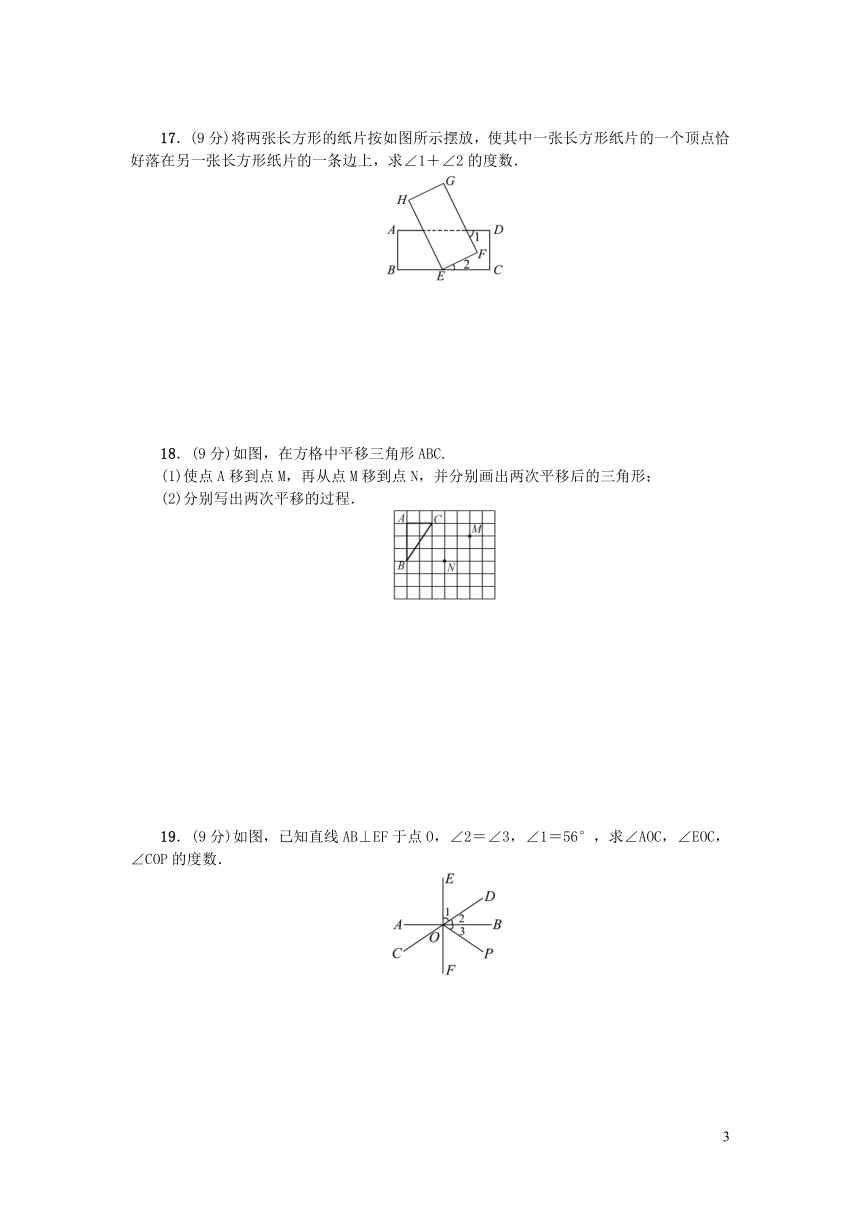
1.下列图形中能肯定∠1=∠2的是(
)
2.过一点画已知直线的平行线,则(
)
A.有且只有一条
B.有无数条
C.不存在
D.不存在或只有一条
3.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件(
)
A.∠1=∠2
B.∠1=∠DFE
C.∠1=∠AFD
D.∠2=∠AFD
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.(2017·北京)如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
5.如图,DE∥AB,若∠ACD=55°,则∠A等于(
)
A.35°
B.55°
C.65°
D.125°
6.在5×5的方格纸中,将图①中的图形N平移后如图②中所示,那么正确的平移方法是(
)
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
7.(2019·陕西)如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为(
)
A.55°
B.75°
C.65°
D.85°
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.如图,已知∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的点Q反射后(∠AQR=∠OQP),反射光线QR恰好与OB平行,则∠QPB等于(
)
A.60°
B.80°
C.100°
D.120°
9.如图,AB∥CD,直线EF交AB于点E,交CD于点F,GE平分∠BEF,交CD于点G,∠1=50°,则∠2等于(
)
A.50°
B.60°
C.65°
D.90°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于(
)
A.180°
B.360°
C.540°
D.720°
二、填空题(每小题3分,共15分)
11.四条直线两两相交,最多有a个交点,最少有b个交点,则a+b=(
).
12.一张宽度相等的纸条按如图所示折叠,则∠1=(
).
,第12题图) ,第13题图) ,第14题图) ,第15题图)
13.如图,计划把河流AB中的水引到岸上的C处,可过点C作CD⊥AB于D,然后沿CD开渠,可使所开的渠道最短,这是因为(
).
14.如图,直线AB,CD相交于点O,OE平分∠BOC,若∠1=75°,则∠2=(
),∠3=(
).
15.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=(
).
三、解答题(共75分)
16.(8分)木工师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线,如图所示,a∥b,你能说明理由吗?
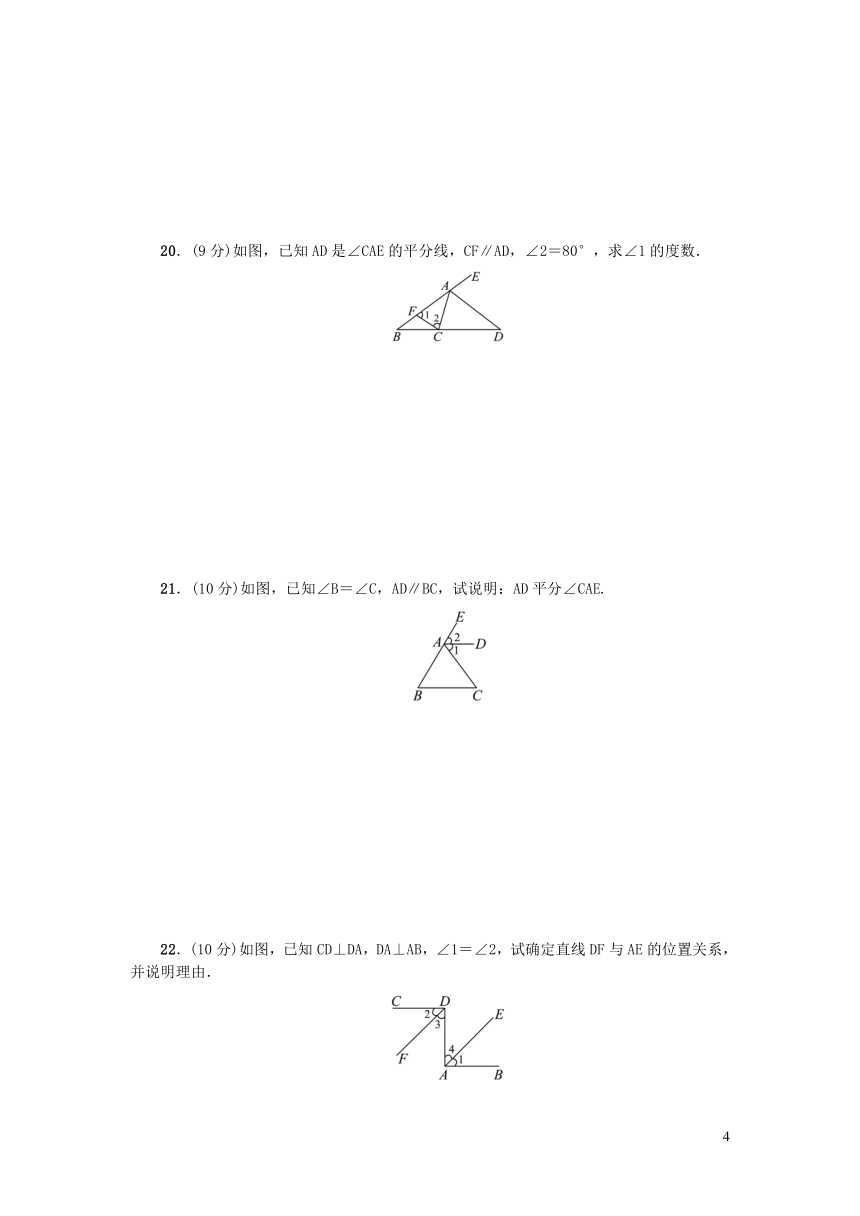
17.(9分)将两张长方形的纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的度数.
18.(9分)如图,在方格中平移三角形ABC.
(1)使点A移到点M,再从点M移到点N,并分别画出两次平移后的三角形;
(2)分别写出两次平移的过程.
19.(9分)如图,已知直线AB⊥EF于点O,∠2=∠3,∠1=56°,求∠AOC,∠EOC,∠COP的度数.
20.(9分)如图,已知AD是∠CAE的平分线,CF∥AD,∠2=80°,求∠1的度数.
21.(10分)如图,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
22.(10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由.
23.(11分)如图,点E在直线DF上,点B在直线AC上,∠FGB+∠EHF=180°.
(1)请问DB与EC平行吗?为什么?
(2)若∠C=∠D,试判断∠A与∠F的关系,并说明理由.
检测内容:相交线与平行线(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列图形中能肯定∠1=∠2的是(
C
)
2.过一点画已知直线的平行线,则(
D
)
A.有且只有一条
B.有无数条
C.不存在
D.不存在或只有一条
3.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件(
B
)
A.∠1=∠2
B.∠1=∠DFE
C.∠1=∠AFD
D.∠2=∠AFD
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.(2017·北京)如图所示,点P到直线l的距离是(
B
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
5.如图,DE∥AB,若∠ACD=55°,则∠A等于(
B
)
A.35°
B.55°
C.65°
D.125°
6.在5×5的方格纸中,将图①中的图形N平移后如图②中所示,那么正确的平移方法是(
C
)
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
7.(2019·陕西)如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为(
C
)
A.55°
B.75°
C.65°
D.85°
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.如图,已知∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的点Q反射后(∠AQR=∠OQP),反射光线QR恰好与OB平行,则∠QPB等于(
B
)
A.60°
B.80°
C.100°
D.120°
9.如图,AB∥CD,直线EF交AB于点E,交CD于点F,GE平分∠BEF,交CD于点G,∠1=50°,则∠2等于(
C
)
A.50°
B.60°
C.65°
D.90°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于(
C
)
A.180°
B.360°
C.540°
D.720°
二、填空题(每小题3分,共15分)
11.四条直线两两相交,最多有a个交点,最少有b个交点,则a+b=__7__.
12.一张宽度相等的纸条按如图所示折叠,则∠1=__60°__.
,第12题图) ,第13题图) ,第14题图) ,第15题图)
13.如图,计划把河流AB中的水引到岸上的C处,可过点C作CD⊥AB于D,然后沿CD开渠,可使所开的渠道最短,这是因为__垂线段最短__.
14.如图,直线AB,CD相交于点O,OE平分∠BOC,若∠1=75°,则∠2=__30°__,∠3=__150°__.
15.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__54°__.
三、解答题(共75分)
16.(8分)木工师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线,如图所示,a∥b,你能说明理由吗?
解:同位角相等,两直线平行
17.(9分)将两张长方形的纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的度数.
解:过点F作FM∥AD,交HE于点M,∴∠1=∠GFM(两直线平行,内错角相等).∵AD∥BC,∴FM∥BC(平行于同一条直线的两条直线平行),∴∠2=∠MFE(两直线平行,内错角相等),∴∠1+∠2=∠GFM+∠MFE.∵∠GFM+∠MFE=90°,∴∠1+∠2=90°
18.(9分)如图,在方格中平移三角形ABC.
(1)使点A移到点M,再从点M移到点N,并分别画出两次平移后的三角形;
(2)分别写出两次平移的过程.
解:(1)略 (2)将三角形ABC先向右平移五格,再向下平移一格到M点;从点M先向下平移两格,再向左平移两格到点N
19.(9分)如图,已知直线AB⊥EF于点O,∠2=∠3,∠1=56°,求∠AOC,∠EOC,∠COP的度数.
解:∵AB⊥EF,∴∠EOB=∠AOE=∠1+∠2=90°,又∠1=56°,∴∠2=34°=∠AOC.∠EOC=∠AOE+∠AOC=90°+34°=124°.∠COP=180°-∠2-∠3=180°-2∠2=180°-2×34°=112°
20.(9分)如图,已知AD是∠CAE的平分线,CF∥AD,∠2=80°,求∠1的度数.
解:因为CF∥AD,所以∠1=∠EAD,∠2=∠CAD,因为AD平分∠CAE,所以∠EAD=∠CAD,则∠1=∠2,因为∠2=80°,所以∠1=80°
21.(10分)如图,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
解:由AD∥BC,得∠B=∠2,∠C=∠1,又∠B=∠C,所以∠1=∠2
22.(10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由.
解:DF∥AE 理由:因为CD⊥DA,DA⊥AB,所以∠CDA=∠DAB=90°,又因为∠1=∠2,所以90°-∠1=90°-∠2,即∠3=∠4,所以DF∥AE
23.(11分)如图,点E在直线DF上,点B在直线AC上,∠FGB+∠EHF=180°.
(1)请问DB与EC平行吗?为什么?
(2)若∠C=∠D,试判断∠A与∠F的关系,并说明理由.
解:(1)DB∥EC.理由如下:∵∠FGB+∠EHF=180°,∠EHF=∠GHC,∴∠FGB+∠GHC=180°,∴DB∥EC (2)∠A=∠F.理由如下:∵DB∥EC,∴∠C=∠DBA.∵∠C=∠D,∴∠DBA=∠D,∴AC∥DF,∴∠A=∠F
1
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列图形中能肯定∠1=∠2的是(
)
2.过一点画已知直线的平行线,则(
)
A.有且只有一条
B.有无数条
C.不存在
D.不存在或只有一条
3.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件(
)
A.∠1=∠2
B.∠1=∠DFE
C.∠1=∠AFD
D.∠2=∠AFD
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.(2017·北京)如图所示,点P到直线l的距离是(
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
5.如图,DE∥AB,若∠ACD=55°,则∠A等于(
)
A.35°
B.55°
C.65°
D.125°
6.在5×5的方格纸中,将图①中的图形N平移后如图②中所示,那么正确的平移方法是(
)
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
7.(2019·陕西)如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为(
)
A.55°
B.75°
C.65°
D.85°
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.如图,已知∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的点Q反射后(∠AQR=∠OQP),反射光线QR恰好与OB平行,则∠QPB等于(
)
A.60°
B.80°
C.100°
D.120°
9.如图,AB∥CD,直线EF交AB于点E,交CD于点F,GE平分∠BEF,交CD于点G,∠1=50°,则∠2等于(
)
A.50°
B.60°
C.65°
D.90°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于(
)
A.180°
B.360°
C.540°
D.720°
二、填空题(每小题3分,共15分)
11.四条直线两两相交,最多有a个交点,最少有b个交点,则a+b=(
).
12.一张宽度相等的纸条按如图所示折叠,则∠1=(
).
,第12题图) ,第13题图) ,第14题图) ,第15题图)
13.如图,计划把河流AB中的水引到岸上的C处,可过点C作CD⊥AB于D,然后沿CD开渠,可使所开的渠道最短,这是因为(
).
14.如图,直线AB,CD相交于点O,OE平分∠BOC,若∠1=75°,则∠2=(
),∠3=(
).
15.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=(
).
三、解答题(共75分)
16.(8分)木工师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线,如图所示,a∥b,你能说明理由吗?
17.(9分)将两张长方形的纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的度数.
18.(9分)如图,在方格中平移三角形ABC.
(1)使点A移到点M,再从点M移到点N,并分别画出两次平移后的三角形;
(2)分别写出两次平移的过程.
19.(9分)如图,已知直线AB⊥EF于点O,∠2=∠3,∠1=56°,求∠AOC,∠EOC,∠COP的度数.
20.(9分)如图,已知AD是∠CAE的平分线,CF∥AD,∠2=80°,求∠1的度数.
21.(10分)如图,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
22.(10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由.
23.(11分)如图,点E在直线DF上,点B在直线AC上,∠FGB+∠EHF=180°.
(1)请问DB与EC平行吗?为什么?
(2)若∠C=∠D,试判断∠A与∠F的关系,并说明理由.
检测内容:相交线与平行线(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题3分,共30分)
1.下列图形中能肯定∠1=∠2的是(
C
)
2.过一点画已知直线的平行线,则(
D
)
A.有且只有一条
B.有无数条
C.不存在
D.不存在或只有一条
3.如图,点D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需再有条件(
B
)
A.∠1=∠2
B.∠1=∠DFE
C.∠1=∠AFD
D.∠2=∠AFD
,第3题图) ,第4题图) ,第5题图) ,第6题图)
4.(2017·北京)如图所示,点P到直线l的距离是(
B
)
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
5.如图,DE∥AB,若∠ACD=55°,则∠A等于(
B
)
A.35°
B.55°
C.65°
D.125°
6.在5×5的方格纸中,将图①中的图形N平移后如图②中所示,那么正确的平移方法是(
C
)
A.先向下平移1格,再向左平移1格
B.先向下平移1格,再向左平移2格
C.先向下平移2格,再向左平移1格
D.先向下平移2格,再向左平移2格
7.(2019·陕西)如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=25°,则∠2的大小为(
C
)
A.55°
B.75°
C.65°
D.85°
,第7题图) ,第8题图) ,第9题图) ,第10题图)
8.如图,已知∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的点Q反射后(∠AQR=∠OQP),反射光线QR恰好与OB平行,则∠QPB等于(
B
)
A.60°
B.80°
C.100°
D.120°
9.如图,AB∥CD,直线EF交AB于点E,交CD于点F,GE平分∠BEF,交CD于点G,∠1=50°,则∠2等于(
C
)
A.50°
B.60°
C.65°
D.90°
10.如图,AB∥CD,则∠A+∠E+∠F+∠C等于(
C
)
A.180°
B.360°
C.540°
D.720°
二、填空题(每小题3分,共15分)
11.四条直线两两相交,最多有a个交点,最少有b个交点,则a+b=__7__.
12.一张宽度相等的纸条按如图所示折叠,则∠1=__60°__.
,第12题图) ,第13题图) ,第14题图) ,第15题图)
13.如图,计划把河流AB中的水引到岸上的C处,可过点C作CD⊥AB于D,然后沿CD开渠,可使所开的渠道最短,这是因为__垂线段最短__.
14.如图,直线AB,CD相交于点O,OE平分∠BOC,若∠1=75°,则∠2=__30°__,∠3=__150°__.
15.如图,点B,C,D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__54°__.
三、解答题(共75分)
16.(8分)木工师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线,如图所示,a∥b,你能说明理由吗?
解:同位角相等,两直线平行
17.(9分)将两张长方形的纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的度数.
解:过点F作FM∥AD,交HE于点M,∴∠1=∠GFM(两直线平行,内错角相等).∵AD∥BC,∴FM∥BC(平行于同一条直线的两条直线平行),∴∠2=∠MFE(两直线平行,内错角相等),∴∠1+∠2=∠GFM+∠MFE.∵∠GFM+∠MFE=90°,∴∠1+∠2=90°
18.(9分)如图,在方格中平移三角形ABC.
(1)使点A移到点M,再从点M移到点N,并分别画出两次平移后的三角形;
(2)分别写出两次平移的过程.
解:(1)略 (2)将三角形ABC先向右平移五格,再向下平移一格到M点;从点M先向下平移两格,再向左平移两格到点N
19.(9分)如图,已知直线AB⊥EF于点O,∠2=∠3,∠1=56°,求∠AOC,∠EOC,∠COP的度数.
解:∵AB⊥EF,∴∠EOB=∠AOE=∠1+∠2=90°,又∠1=56°,∴∠2=34°=∠AOC.∠EOC=∠AOE+∠AOC=90°+34°=124°.∠COP=180°-∠2-∠3=180°-2∠2=180°-2×34°=112°
20.(9分)如图,已知AD是∠CAE的平分线,CF∥AD,∠2=80°,求∠1的度数.
解:因为CF∥AD,所以∠1=∠EAD,∠2=∠CAD,因为AD平分∠CAE,所以∠EAD=∠CAD,则∠1=∠2,因为∠2=80°,所以∠1=80°
21.(10分)如图,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
解:由AD∥BC,得∠B=∠2,∠C=∠1,又∠B=∠C,所以∠1=∠2
22.(10分)如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由.
解:DF∥AE 理由:因为CD⊥DA,DA⊥AB,所以∠CDA=∠DAB=90°,又因为∠1=∠2,所以90°-∠1=90°-∠2,即∠3=∠4,所以DF∥AE
23.(11分)如图,点E在直线DF上,点B在直线AC上,∠FGB+∠EHF=180°.
(1)请问DB与EC平行吗?为什么?
(2)若∠C=∠D,试判断∠A与∠F的关系,并说明理由.
解:(1)DB∥EC.理由如下:∵∠FGB+∠EHF=180°,∠EHF=∠GHC,∴∠FGB+∠GHC=180°,∴DB∥EC (2)∠A=∠F.理由如下:∵DB∥EC,∴∠C=∠DBA.∵∠C=∠D,∴∠DBA=∠D,∴AC∥DF,∴∠A=∠F
1
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
