2.4.2 有理数的加法课件(共24张PPT)
文档属性
| 名称 | 2.4.2 有理数的加法课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览








文档简介
2.4 有理数的加法(一)
第二章
有理数及其运算
2020年秋季北师大版七年级上册
1. 叙述有理数的加法法则.
(1)(-2)+(-3)= -5 ; 3 + 2 = 5
同号两数相加,取相同的符号,并把绝对值相加。
(2)(-3)+ 2 = - 1;3 +(-2)= 1 ;4+(- 4)= 0
异号两数相加,绝对值相等时和为0;
绝对值不相等时,取绝对值大的数的符号,
并用较大的绝对值减去较小的绝对值。
(3) 0 +(- 4)= - 4 ;4 + 0 = 4
一个数同零相加,仍得这个数。
一、复习回顾
2 .计算并比较每组的两个算式的结果:
(1) (-8)+(-9)与 (-9)+(-8);
(2) 4 +(-7)与 (-7) + 4;
(3) [2+(-3)]+(-8)与2+[(-3)+(-8)];
(4) [10+(-10)]+(-5)与 10+[(-10)+(-5)]
小学学过的加法运算律是不是也可以扩充到有理数范围?
二、探究新知
有理数的加法中,两个数相加,交换加数的位置和不变。
加法交换律:a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。
加法结合律:(a+b)+c=a+(b+c)
解:(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32)??????? (加法交换律)
=(16+24)+[(-25)+(-32)] ?(加法结合律)
=40+(-57)???????????????????????? (同号相加法则)
=-17???????????????????????????? ?(异号相加法则)
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
解:(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
解:(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
常用的三个规律:
1、 把正数或负数分别结合在一起相加。
2、有相反数的先把相反数相加,能凑整的先凑整。
3、有分母相同的,先把分母相同的数结合相加。
此题你是抓住数的什么特点使计算简化的?
依据是什么?
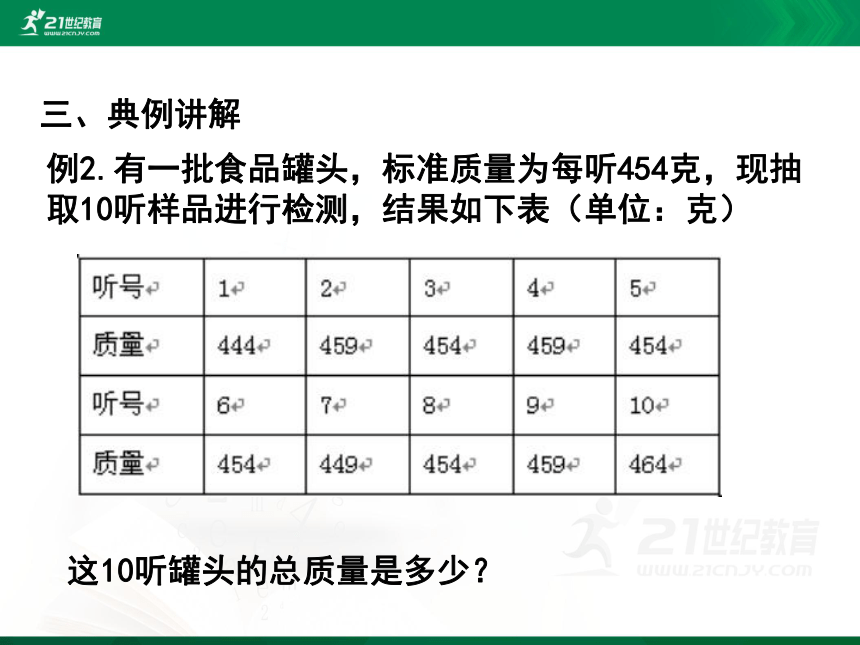
例2.有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表(单位:克)
这10听罐头的总质量是多少?
三、典例讲解
解法一:这10听罐头的总质量为
444+459+454+459+454++454+449+454++459+464
=4550(克)
三、典例讲解
解法二:把超过标准质量的克数用正数表示,不足的用负数表示,10听罐头与标准质量的差值表(单位:克)
这10听罐头与标准质量差值的和为
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
=[(-10)+10]+[(-5)+5]+5+5=10(克)
∴这10听罐头的总质量为
454×10 + 10
= 4540 + 10
= 4550
1.7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是运用了( )
A. 加法交换律 B. 加法结合律
C. 加法交换律与结合律 D. 以上都不对
C
四、课堂检测
2.计算 ,比较合适的做法是( )
A. 把一、三两个加数结合,二、四两个加数结合
B. 把一、二两个加数结合,三、四两个加数结合
C. 把一、四两个加数结合,二、三两个加数结合
D. 把一、二、四这三个加数先结合
A
3. 下列计算结果是负数的是( )
A. 3+(-12)+9 B. 5+(-11)+7
C. (-7)+(-6)+12 D. (-5)+10+(-2)
C
四、课堂检测
4. 七年级(1)班一学期班费收支情况如下(收入为正):+250元,-55元,-120元,+7元. 该班期末时,班费结余为( )
A. 82元 B. 85元 C. 35元 D. 92元
A
5. 下列运算中正确的是( )
A. 8+[14+(-19)]=13
B. (-2.5)+[5+(-2.5)]=5
C.
D. 3.14+[(-8)+3.14]=-8
C
四、课堂检测
6.计算:
(1)(-27)+32+(-23)+24;
解: (1)(-27)+32+(-23)+24
=(-27)+(-23)+32+24
=[(-27)+(-23)]+(32+24)
=(-50)+56
=6.
四、课堂检测
(2)
解:
四、课堂检测
(3)(+26)+(-18)+5+(-16);
(4)16.58+(-3.8)+5.2+(-0.2)+(-0.58)+(-5.2).
解:(1)原式=[26+(-16)]+[(-18)+5]
=10+(-13)
=-3.
(2)原式=[16.58+(-0.58)]+[(-3.8)+(-0.2)]+[5.2+(-5.2)]
=16+(-4)+0
=12.
四、课堂检测
7.有5筐蔬菜,以每筐50千克为准,超过的千克数记为正,不足记为负,称重记录如下:
5筐蔬菜的总重量是多少千克?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}筐号
1
2
3
4
5
重量
+3
-6
-4
+2
-1
解:这5筐蔬菜与标准质量差值的和为
3+(-6)+(-4)+ 2 + (-1)= -6 (千克)
因此,这5筐蔬菜的总重量为
50×5 + (-6)= 250 +(-6)= 244克)
四、课堂检测
8. 一口3 m深的井,一只蜗牛从井底沿着井壁往井口爬:
第一次往上爬了0.5 m,又下滑了0.1 m;
第二次往上爬了0.42 m,又下滑了0.15 m;
第三次往上爬了0.7 m,又下滑了0.15 m;
第四次往上爬了0.75 m,又下滑了0.1 m;
第五次往上爬了0.55 m,没有下滑;
第六次往上爬了0.48 m,
问此时蜗牛有没有爬出井口?
四、课堂检测
解:将往上爬记为正,下滑记为负,则
0.5+(-0.1)+0.42+(-0.15)+0.7+(-0.15)+0.75+
(-0.1)+0.55+0.48
=(0.5+0.42+0.7+0.75+0.55+0.48)+[(-0.1)+
(-0.15)+(-0.15)+(-0.1)]
=2.9(m)<3(m).
答: 此时蜗牛没有爬出井口.
四、课堂检测
9. 某人用400元买了8套儿童服装,准备以一定价格出售,若每套以55元的价格为标准,超出的记作正数,不足的记为负数,记录如下:+2,-3,+2,+1,-2,-1,0,-2.当他卖完这8套服装,最后的盈亏情况是怎样的.
四、课堂检测
解:8套服装的总售价为
8×55+2+(-3)+(+2)+(+1)+(-2)+(-1)+0+(-2)
=440+(-3)=437(元).
8套服装的总成本为400元,所以盈利为
437-400=37(元).
答:最后盈利37元.
五,本节小结:
1.通过具体有理数的计算,把加法运算律从非负数
范围扩大到有理数的范围。
2.掌握加法运算律的法则及公式,并适当的运用运
算律进行简化计算。
3.有理数加法解决实际问题,体会求简意识。
六、布置作业
课本P36习题2.4 第1、2、3、4 题
谢谢
第二章
有理数及其运算
2020年秋季北师大版七年级上册
1. 叙述有理数的加法法则.
(1)(-2)+(-3)= -5 ; 3 + 2 = 5
同号两数相加,取相同的符号,并把绝对值相加。
(2)(-3)+ 2 = - 1;3 +(-2)= 1 ;4+(- 4)= 0
异号两数相加,绝对值相等时和为0;
绝对值不相等时,取绝对值大的数的符号,
并用较大的绝对值减去较小的绝对值。
(3) 0 +(- 4)= - 4 ;4 + 0 = 4
一个数同零相加,仍得这个数。
一、复习回顾
2 .计算并比较每组的两个算式的结果:
(1) (-8)+(-9)与 (-9)+(-8);
(2) 4 +(-7)与 (-7) + 4;
(3) [2+(-3)]+(-8)与2+[(-3)+(-8)];
(4) [10+(-10)]+(-5)与 10+[(-10)+(-5)]
小学学过的加法运算律是不是也可以扩充到有理数范围?
二、探究新知
有理数的加法中,两个数相加,交换加数的位置和不变。
加法交换律:a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。
加法结合律:(a+b)+c=a+(b+c)
解:(1) 16+(-25)+24+(-32)
=16+24+(-25)+(-32)??????? (加法交换律)
=(16+24)+[(-25)+(-32)] ?(加法结合律)
=40+(-57)???????????????????????? (同号相加法则)
=-17???????????????????????????? ?(异号相加法则)
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
解:(2)31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ] (加法交换律和结合律 )
=100+0
=100
例1 计算
(1) 16+(-25)+24+(-32); (2) 31 +(-28)+ 28 + 69
三、典例讲解
(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
解:(3) —+ (- —) + (- —) + (+ —)
1
6
2
7
6
5
5
7
常用的三个规律:
1、 把正数或负数分别结合在一起相加。
2、有相反数的先把相反数相加,能凑整的先凑整。
3、有分母相同的,先把分母相同的数结合相加。
此题你是抓住数的什么特点使计算简化的?
依据是什么?
例2.有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表(单位:克)
这10听罐头的总质量是多少?
三、典例讲解
解法一:这10听罐头的总质量为
444+459+454+459+454++454+449+454++459+464
=4550(克)
三、典例讲解
解法二:把超过标准质量的克数用正数表示,不足的用负数表示,10听罐头与标准质量的差值表(单位:克)
这10听罐头与标准质量差值的和为
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
=[(-10)+10]+[(-5)+5]+5+5=10(克)
∴这10听罐头的总质量为
454×10 + 10
= 4540 + 10
= 4550
1.7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是运用了( )
A. 加法交换律 B. 加法结合律
C. 加法交换律与结合律 D. 以上都不对
C
四、课堂检测
2.计算 ,比较合适的做法是( )
A. 把一、三两个加数结合,二、四两个加数结合
B. 把一、二两个加数结合,三、四两个加数结合
C. 把一、四两个加数结合,二、三两个加数结合
D. 把一、二、四这三个加数先结合
A
3. 下列计算结果是负数的是( )
A. 3+(-12)+9 B. 5+(-11)+7
C. (-7)+(-6)+12 D. (-5)+10+(-2)
C
四、课堂检测
4. 七年级(1)班一学期班费收支情况如下(收入为正):+250元,-55元,-120元,+7元. 该班期末时,班费结余为( )
A. 82元 B. 85元 C. 35元 D. 92元
A
5. 下列运算中正确的是( )
A. 8+[14+(-19)]=13
B. (-2.5)+[5+(-2.5)]=5
C.
D. 3.14+[(-8)+3.14]=-8
C
四、课堂检测
6.计算:
(1)(-27)+32+(-23)+24;
解: (1)(-27)+32+(-23)+24
=(-27)+(-23)+32+24
=[(-27)+(-23)]+(32+24)
=(-50)+56
=6.
四、课堂检测
(2)
解:
四、课堂检测
(3)(+26)+(-18)+5+(-16);
(4)16.58+(-3.8)+5.2+(-0.2)+(-0.58)+(-5.2).
解:(1)原式=[26+(-16)]+[(-18)+5]
=10+(-13)
=-3.
(2)原式=[16.58+(-0.58)]+[(-3.8)+(-0.2)]+[5.2+(-5.2)]
=16+(-4)+0
=12.
四、课堂检测
7.有5筐蔬菜,以每筐50千克为准,超过的千克数记为正,不足记为负,称重记录如下:
5筐蔬菜的总重量是多少千克?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}筐号
1
2
3
4
5
重量
+3
-6
-4
+2
-1
解:这5筐蔬菜与标准质量差值的和为
3+(-6)+(-4)+ 2 + (-1)= -6 (千克)
因此,这5筐蔬菜的总重量为
50×5 + (-6)= 250 +(-6)= 244克)
四、课堂检测
8. 一口3 m深的井,一只蜗牛从井底沿着井壁往井口爬:
第一次往上爬了0.5 m,又下滑了0.1 m;
第二次往上爬了0.42 m,又下滑了0.15 m;
第三次往上爬了0.7 m,又下滑了0.15 m;
第四次往上爬了0.75 m,又下滑了0.1 m;
第五次往上爬了0.55 m,没有下滑;
第六次往上爬了0.48 m,
问此时蜗牛有没有爬出井口?
四、课堂检测
解:将往上爬记为正,下滑记为负,则
0.5+(-0.1)+0.42+(-0.15)+0.7+(-0.15)+0.75+
(-0.1)+0.55+0.48
=(0.5+0.42+0.7+0.75+0.55+0.48)+[(-0.1)+
(-0.15)+(-0.15)+(-0.1)]
=2.9(m)<3(m).
答: 此时蜗牛没有爬出井口.
四、课堂检测
9. 某人用400元买了8套儿童服装,准备以一定价格出售,若每套以55元的价格为标准,超出的记作正数,不足的记为负数,记录如下:+2,-3,+2,+1,-2,-1,0,-2.当他卖完这8套服装,最后的盈亏情况是怎样的.
四、课堂检测
解:8套服装的总售价为
8×55+2+(-3)+(+2)+(+1)+(-2)+(-1)+0+(-2)
=440+(-3)=437(元).
8套服装的总成本为400元,所以盈利为
437-400=37(元).
答:最后盈利37元.
五,本节小结:
1.通过具体有理数的计算,把加法运算律从非负数
范围扩大到有理数的范围。
2.掌握加法运算律的法则及公式,并适当的运用运
算律进行简化计算。
3.有理数加法解决实际问题,体会求简意识。
六、布置作业
课本P36习题2.4 第1、2、3、4 题
谢谢
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
