人教版数学八年级上册第十一章 三角形 数学活动 镶嵌 课件(39张)
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角形 数学活动 镶嵌 课件(39张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 08:38:27 | ||
图片预览






文档简介
(共39张PPT)
人教版八年级数学第十一章
我们经常见到各种建筑物的地板,能发现地板常用各种地砖铺砌成美丽的图案.
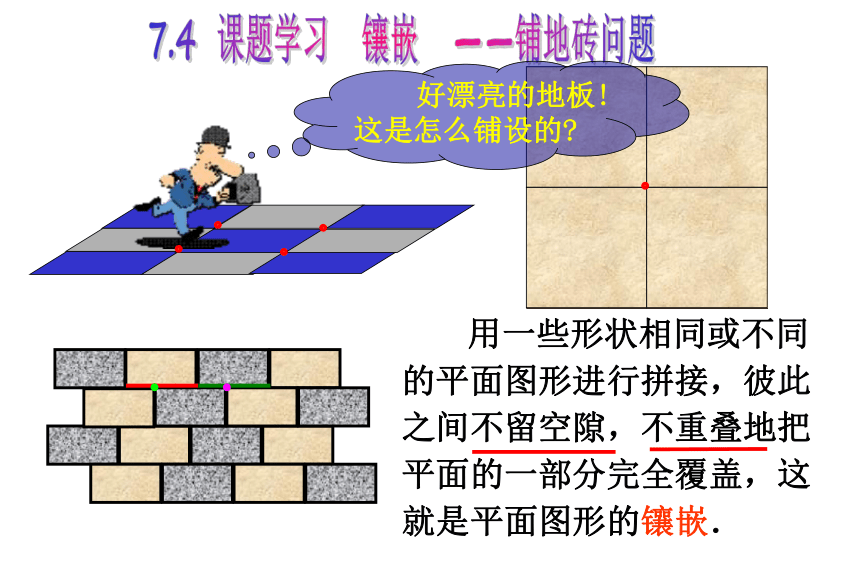
用一些形状相同或不同的平面图形进行拼接,彼此之间不留空隙,不重叠地把平面的一部分完全覆盖,这就是平面图形的镶嵌.
好漂亮的地板!这是怎么铺设的?
教学重点:会用正多边形无缝隙、不重叠地覆盖平面
教学难点:用正多边形无缝隙、不重叠地覆盖平面结论的推导
教学目标:
能力目标:
让学生在应用已有的数学知识和能力,探索和解决镶嵌问题的过程中,感受数学知识的价值,增强应用意识,获得各种体验。
情感目标:体会转化的数学思想,激发学生学习的兴趣.
知识目标:
会用正多边形无缝隙、不重叠地覆盖平面。
请各小组选择自己喜欢的图形拼一拼,看看你能用哪些多边形镶嵌成平面图案?并说明你为什么选择这种图形并能够拼出这样的图案?
只用一种多边形能进行镶嵌吗?
问题
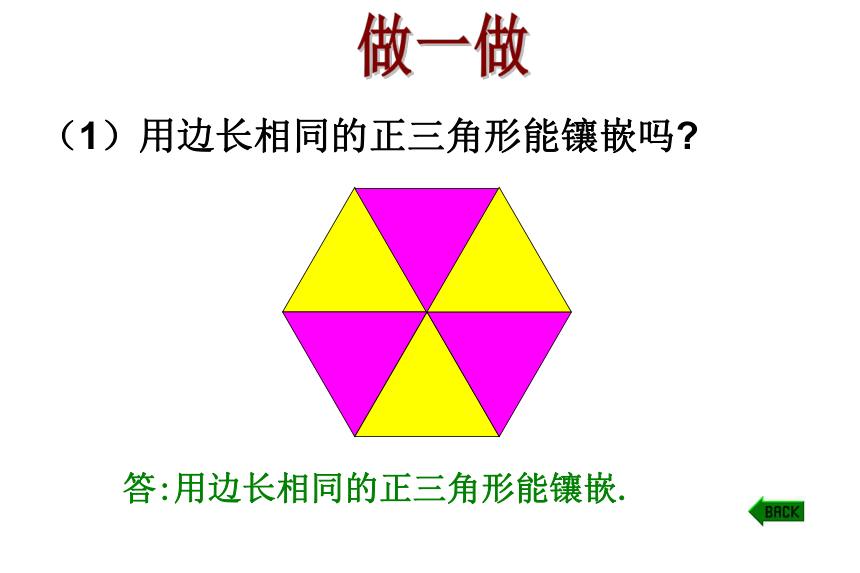
(1)用边长相同的正三角形能镶嵌吗?
答:用边长相同的正三角形能镶嵌.
(2)用边长相同的正方形能镶嵌吗?
答:用边长相同的正方形能镶嵌.
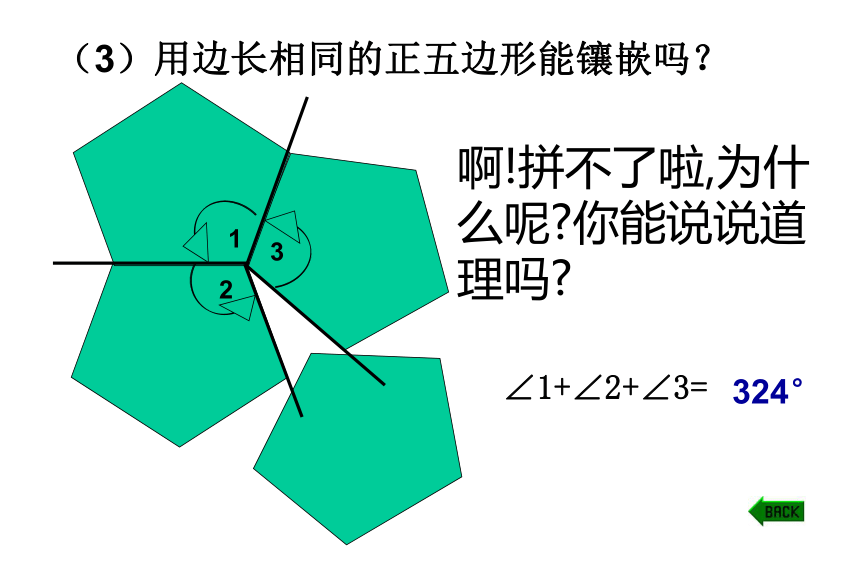
啊!拼不了啦,为什么呢?你能说说道理吗?
1
2
3
∠1+∠2+∠3=
?
(3)用边长相同的正五边形能镶嵌吗?
324°
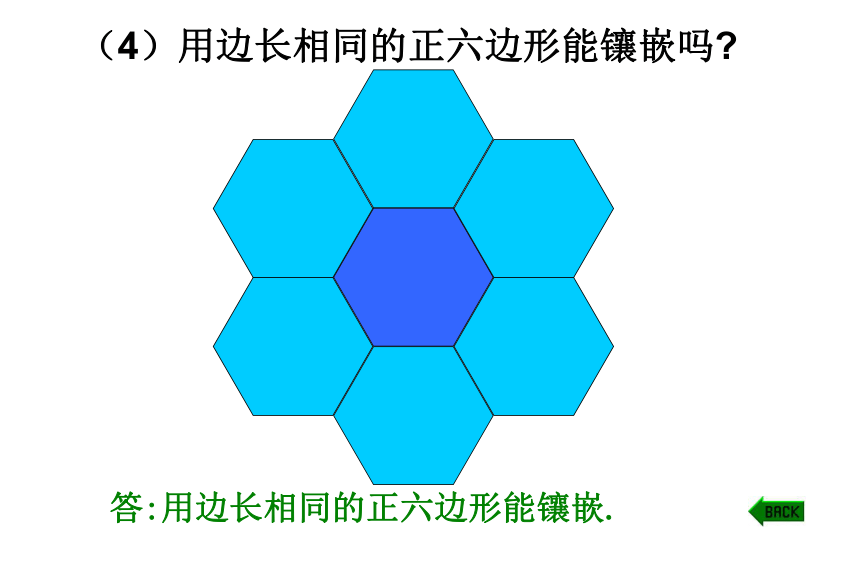
(4)用边长相同的正六边形能镶嵌吗?
答:用边长相同的正六边形能镶嵌.
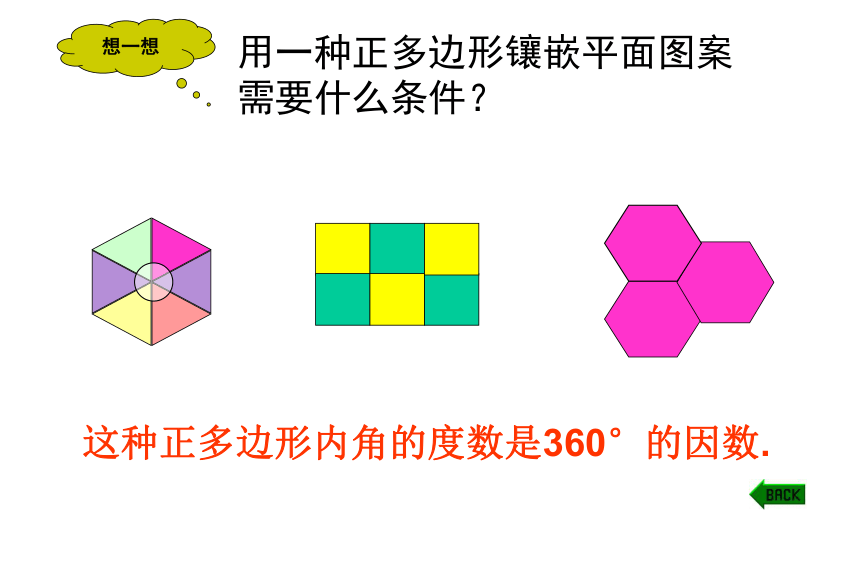
用一种正多边形镶嵌平面图案需要什么条件?
这种正多边形内角的度数是360°的因数.
想一想
你还能找到能镶嵌的其他正多边形吗?
要用一个正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角是否是360°的约数,例如,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的每一个内角都是360°的约数.所以说:在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可镶嵌.
做一做
用任意三角形进行平面镶嵌.
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
∠1+∠2+∠3=180°
做一做
用任意四边形进行平面镶嵌.
∠1+∠2+∠3+∠4=360°
用同一种任意三角形或四边形可以覆盖一部分平面,因为任意三角形的内角和是180°,任意四边形的内角和是360°,它们都是360°的因数,所以可以进行平面镶嵌.
如果用其中两种正多边形镶嵌,哪两种正多边形能镶嵌成平面图案?
问题
A
D
B
C
(1)正三角形与正方形.
(2)正三角形与正五边形.
(3)正三角形与正六边形.
(4)正四边形与正五形.
(5)正四边形与正六形.
(6)正五边形与正六形.
用两种正多边形镶嵌平面图案需要什么条件?
共顶点的角之和等于360°,相邻的多边形有公共边.
想一想
思考:你还能找到其他用两种(或以上)的正多边形镶嵌的平面图案吗?
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
课堂小结
一般地,多边形能覆盖平面需要满足的条件是:
(1)拼接在同一个点的各个角的和恰好等于360°(周角);
(2)相邻的多边形有公共边.
作
业
请同学们充分发挥自己的创造力,设计一幅由多边形镶嵌而成的优美图案,并尝试写上一两句贴切的解说词.
埃舍尔艺术作品
埃舍尔艺术作品
小
结
S
h
u
x
u
e
台州市书生中学朱仁江制作
课
下
人教版八年级数学第十一章
我们经常见到各种建筑物的地板,能发现地板常用各种地砖铺砌成美丽的图案.
用一些形状相同或不同的平面图形进行拼接,彼此之间不留空隙,不重叠地把平面的一部分完全覆盖,这就是平面图形的镶嵌.
好漂亮的地板!这是怎么铺设的?
教学重点:会用正多边形无缝隙、不重叠地覆盖平面
教学难点:用正多边形无缝隙、不重叠地覆盖平面结论的推导
教学目标:
能力目标:
让学生在应用已有的数学知识和能力,探索和解决镶嵌问题的过程中,感受数学知识的价值,增强应用意识,获得各种体验。
情感目标:体会转化的数学思想,激发学生学习的兴趣.
知识目标:
会用正多边形无缝隙、不重叠地覆盖平面。
请各小组选择自己喜欢的图形拼一拼,看看你能用哪些多边形镶嵌成平面图案?并说明你为什么选择这种图形并能够拼出这样的图案?
只用一种多边形能进行镶嵌吗?
问题
(1)用边长相同的正三角形能镶嵌吗?
答:用边长相同的正三角形能镶嵌.
(2)用边长相同的正方形能镶嵌吗?
答:用边长相同的正方形能镶嵌.
啊!拼不了啦,为什么呢?你能说说道理吗?
1
2
3
∠1+∠2+∠3=
?
(3)用边长相同的正五边形能镶嵌吗?
324°
(4)用边长相同的正六边形能镶嵌吗?
答:用边长相同的正六边形能镶嵌.
用一种正多边形镶嵌平面图案需要什么条件?
这种正多边形内角的度数是360°的因数.
想一想
你还能找到能镶嵌的其他正多边形吗?
要用一个正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角是否是360°的约数,例如,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的每一个内角都是360°的约数.所以说:在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可镶嵌.
做一做
用任意三角形进行平面镶嵌.
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
∠1+∠2+∠3=180°
做一做
用任意四边形进行平面镶嵌.
∠1+∠2+∠3+∠4=360°
用同一种任意三角形或四边形可以覆盖一部分平面,因为任意三角形的内角和是180°,任意四边形的内角和是360°,它们都是360°的因数,所以可以进行平面镶嵌.
如果用其中两种正多边形镶嵌,哪两种正多边形能镶嵌成平面图案?
问题
A
D
B
C
(1)正三角形与正方形.
(2)正三角形与正五边形.
(3)正三角形与正六边形.
(4)正四边形与正五形.
(5)正四边形与正六形.
(6)正五边形与正六形.
用两种正多边形镶嵌平面图案需要什么条件?
共顶点的角之和等于360°,相邻的多边形有公共边.
想一想
思考:你还能找到其他用两种(或以上)的正多边形镶嵌的平面图案吗?
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
课堂小结
一般地,多边形能覆盖平面需要满足的条件是:
(1)拼接在同一个点的各个角的和恰好等于360°(周角);
(2)相邻的多边形有公共边.
作
业
请同学们充分发挥自己的创造力,设计一幅由多边形镶嵌而成的优美图案,并尝试写上一两句贴切的解说词.
埃舍尔艺术作品
埃舍尔艺术作品
小
结
S
h
u
x
u
e
台州市书生中学朱仁江制作
课
下
