人教版数学八年级上册第11章 三角形复习课课件(35张)
文档属性
| 名称 | 人教版数学八年级上册第11章 三角形复习课课件(35张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 12:00:19 | ||
图片预览








文档简介
(共35张PPT)
三角形
人教版八年级数学第十一章
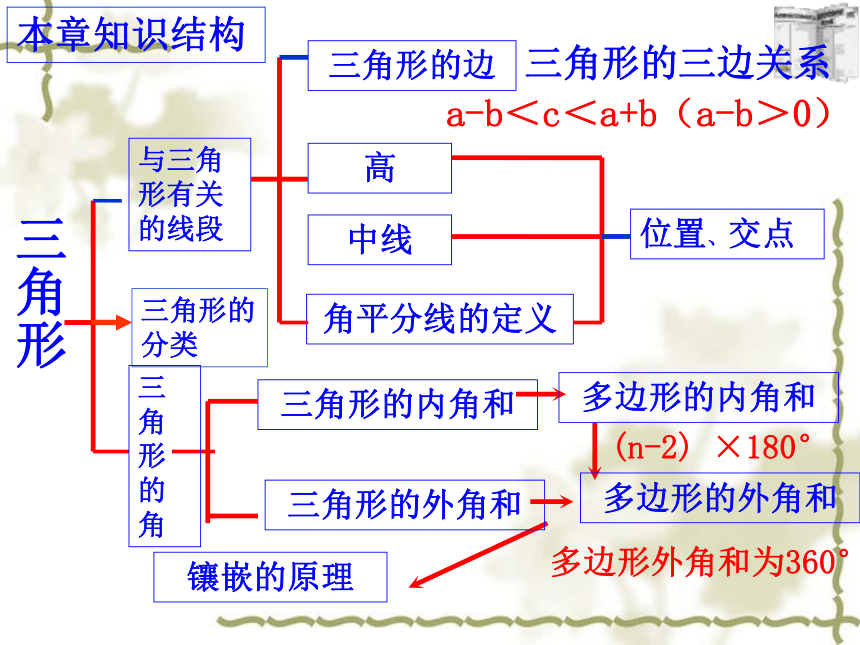
(n-2)
×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的三边关系
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
三角形的分类
数学思想:
整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
1.
三角形的三边关系:
(1)
三角形两边的和大于第三边
2.
判断三条已知线段a、b、c能否
组成三角形.
当a最长,且有b+c>a时,就可构成三角形.
3.
确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
(2)
三角形两边的差小于第三边
1、下列条件中能组成三角形的是(
)
A、
5cm,
13cm,
7cm
B、
3cm,
5cm,
9cm
C、
14cm,
9cm,
6cm
D、
5cm,
6cm,
11cm
C
2、三角形的两边为7cm和5cm,则第三边x的
范围是_____________;
2cm<X
<12cm
练一练
3、等腰三角形一边的长是5
,另一边的长是8,则它的周长是
。
4、一个三角形的两边长分别是2cm
和9cm
,第三边的长为奇数,则第三边的长为_____
.
18或21
从三角形的一个顶点向它的对边所在直线作垂线,_______________的线段叫做三角形的高线.
三角形的高线定义:
顶点和垂足之间
4
三角形的主要线段
三角形角平分线的定义:
顶点与交点
三角形一个角的平分线与它的对边相交,这个角的
之间的线段叫做三角形的角平分线。
三角形的中线定义
顶点与它对边中点
连结三角形一个
的线段叫做三角形的中线。
5
三角形的三条高线(或高线所在直线)
交于一点
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在直线交于三角形
外部一点。
6
三角形的三条中线交于三角形内部一点。
7
三角形的三条角平分线交于三角形
内部一点。
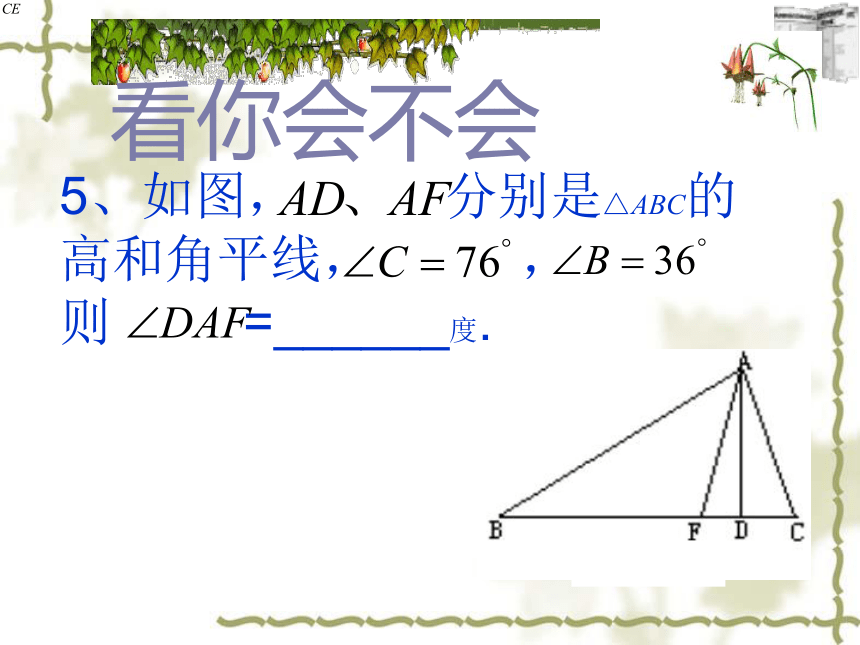
5、如图,
分别是△ABC的高和角平线,
,
则
=______度.
看你会不会
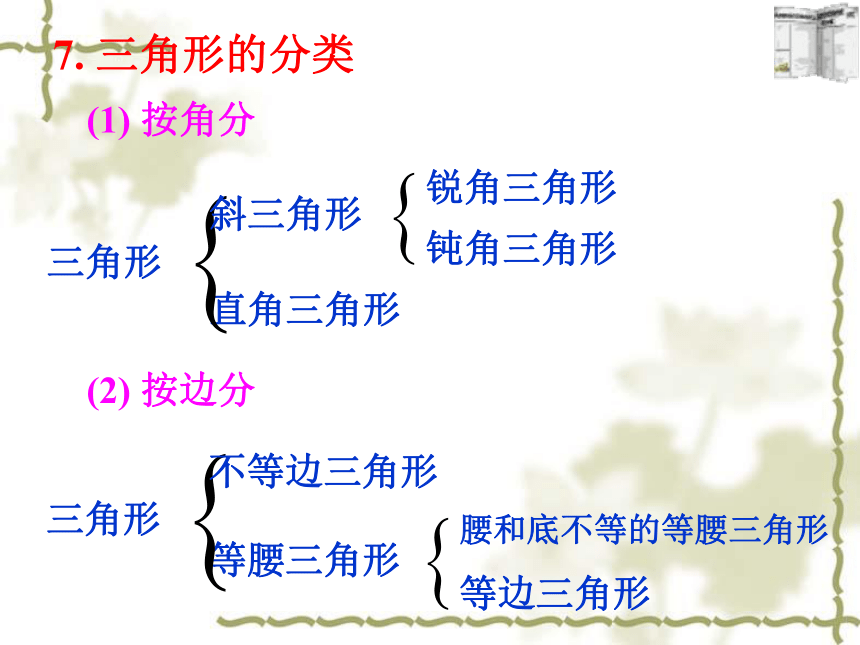
7.
三角形的分类
锐角三角形
三角形
钝角三角形
(1)
按角分
直角三角形
斜三角形
(2)
按边分
腰和底不等的等腰三角形
三角形
等腰三角形
等边三角形
不等边三角形
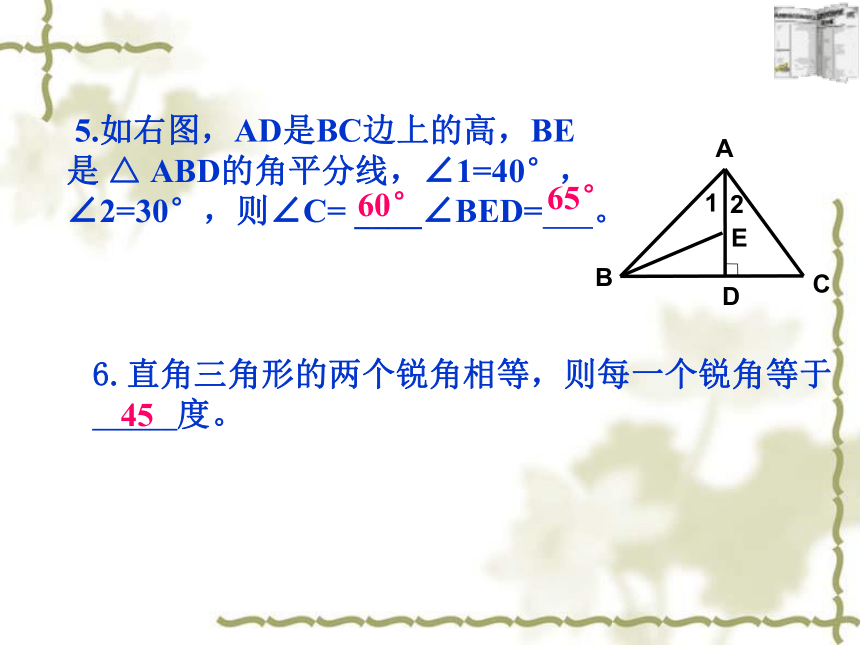
5.如右图,AD是BC边上的高,BE是
△
ABD的角平分线,∠1=40°,∠2=30°,则∠C=
____∠BED=
。
65°
60°
6.直角三角形的两个锐角相等,则每一个锐角等于_____度。
A
B
C
D
1
2
E
45
5.
三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有稳定性,而四边形没有稳定性。
6.
三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
7.
三角形外角和定理
三角形的外角和等于3600
7
木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
三角形具有稳定性
三角形的一个外角等于与它不相邻的两个内角的和。
8.
三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
8.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C=
;
(2)2∠A=∠B+∠C,则∠A=
。
9.如图,______是△ACD的外角,
∠ADB=
115°,∠CAD=
80°则∠C
=___
.
40°
60°
35°
A
B
C
D
∠ADB
练一练
10、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形
75°
钝角
11、如图,已知:AD是△ABC
的中线,△ABC的面积为50cm2
,则△ABD的面积是_______.
25cm2
A
B
C
D
9、n边形的内角和等于(n-2)·180?.
多边形的外角和都等于360°.
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)×
180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
n-3
n-2
3×1800
4×1800
(n-2)×1800
1
2
3
2
3
4
2×1800
3600
3600
3600
3600
答:15边形的内角和是23400
12
求15边形内角和的度数。
多边形的内角和
n边形的内角和为(n-2)×1800
解:(n-2)×1800
=(15-2)×1800
=
23400
13
一个正多边形每一个内角都是120o,这个多边形是( )
A、正四边形
B、正五边形
C、正六边形
D、正七边形
C
14、镶嵌
2、任意三角形一定可以镶嵌.
4、正六边形可以镶嵌.
3、任意四边形一定可以镶嵌
注意:只用正五边形、正八边
形一种图形不能镶嵌.
1、拼接在同一个点的各个角
的和等于360度
下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;
(1)、(2)、(4)
3.如图,已知:AD是△ABC
的中线,△ABC的面积为
,求
△ABD的面积
A
B
C
D
┓
E
4.求下列图形中X的值
(3)
(2)
(1)
┛
1
D
C
A
B
A
B
C
X
1
2
3
4
7.如图,
△ABC中,
∠A=
∠ABD,
∠C=
∠BDC=
∠ABC,求∠DBC的度数
A
B
C
D
友情提示:把图形内部七边形各角看作外部三角形外角,分析可得
9、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
三角形三个内角的度数分别是(x+y)o,
(x-y)o,xo,且x>y>0,则该三角形有一个内角为
( )
A、30O
B、45O
C、60O
D、90O
把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A、只有一种截法
B、只有两种截法
C、有三种截法
D、有四种截法
等腰三角形的腰长为a,底为X,则X的取值范围是( )
A、0<X<2a
B、0<X<a
C、0<X<a/2
D、0<X≤2a
一、选择题
C
C
A
一个正多边形每一个内角都是120o,这个多边形是( )
A、正四边形
B、正五边形
C、正六边形
D、正七边形
一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为(
)
A、13条
B、14条
C、15条
D、16条
下列说法中,错误的是(
)
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
C
A
D
二、填空题
一个三角形的三边长是整数,周长为5,则最小边为
;
木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
小明绕五边形各边走一圈,他共转了 度。
两多边形的边数分别是m
,n条,且各多边形内角相等,又满足1/m+1/n=1/4,则各取一外角的和为
;
下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;
1
三角形具有稳定性
360
90O
(1)、(2)、(4)
1、如图:D是△ABC中BC边上一点,
试说明2AD<AB+BC+AC。
A
C
D
B
友情提示:由AC+CD>AD与AB+BD>AD相加可得。
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
解:
由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3∴
5
又∵第三边长为奇数,
∴
第三条边长为
7cm、9cm。
3、已知两条线段的长分别是3cm、8cm
,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长?
3、已知一个三角形的三边长3、
a+2、8,则a的取值范围是
。
3
三角形
人教版八年级数学第十一章
(n-2)
×180°
三角形
与三角形有关的线段
a-b<c<a+b(a-b>0)
高
三角形的边
三角形的三边关系
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
本章知识结构
三角形的角
三角形的分类
数学思想:
整体思想和转化思想
在一个图形中同时出现两条角平分线时,常常要用到整体思想.
运用转化思想将复杂的问题转化为简单的问题,将未知的问题转化为已知的问题,是常用的数学方法.
1.
三角形的三边关系:
(1)
三角形两边的和大于第三边
2.
判断三条已知线段a、b、c能否
组成三角形.
当a最长,且有b+c>a时,就可构成三角形.
3.
确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
(2)
三角形两边的差小于第三边
1、下列条件中能组成三角形的是(
)
A、
5cm,
13cm,
7cm
B、
3cm,
5cm,
9cm
C、
14cm,
9cm,
6cm
D、
5cm,
6cm,
11cm
C
2、三角形的两边为7cm和5cm,则第三边x的
范围是_____________;
2cm<X
<12cm
练一练
3、等腰三角形一边的长是5
,另一边的长是8,则它的周长是
。
4、一个三角形的两边长分别是2cm
和9cm
,第三边的长为奇数,则第三边的长为_____
.
18或21
从三角形的一个顶点向它的对边所在直线作垂线,_______________的线段叫做三角形的高线.
三角形的高线定义:
顶点和垂足之间
4
三角形的主要线段
三角形角平分线的定义:
顶点与交点
三角形一个角的平分线与它的对边相交,这个角的
之间的线段叫做三角形的角平分线。
三角形的中线定义
顶点与它对边中点
连结三角形一个
的线段叫做三角形的中线。
5
三角形的三条高线(或高线所在直线)
交于一点
锐角三角形三条高线交于三角形内部一点,
直角三角形三条高线交于直角顶点,
钝角三角形三条高线所在直线交于三角形
外部一点。
6
三角形的三条中线交于三角形内部一点。
7
三角形的三条角平分线交于三角形
内部一点。
5、如图,
分别是△ABC的高和角平线,
,
则
=______度.
看你会不会
7.
三角形的分类
锐角三角形
三角形
钝角三角形
(1)
按角分
直角三角形
斜三角形
(2)
按边分
腰和底不等的等腰三角形
三角形
等腰三角形
等边三角形
不等边三角形
5.如右图,AD是BC边上的高,BE是
△
ABD的角平分线,∠1=40°,∠2=30°,则∠C=
____∠BED=
。
65°
60°
6.直角三角形的两个锐角相等,则每一个锐角等于_____度。
A
B
C
D
1
2
E
45
5.
三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有稳定性,而四边形没有稳定性。
6.
三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
7.
三角形外角和定理
三角形的外角和等于3600
7
木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
三角形具有稳定性
三角形的一个外角等于与它不相邻的两个内角的和。
8.
三角形的外角与内角的关系
三角形的一个外角大于与它不相邻的任何一个内角。
8.在△ABC中,
(1)∠B=100°,∠A=∠C,则∠C=
;
(2)2∠A=∠B+∠C,则∠A=
。
9.如图,______是△ACD的外角,
∠ADB=
115°,∠CAD=
80°则∠C
=___
.
40°
60°
35°
A
B
C
D
∠ADB
练一练
10、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形
75°
钝角
11、如图,已知:AD是△ABC
的中线,△ABC的面积为50cm2
,则△ABD的面积是_______.
25cm2
A
B
C
D
9、n边形的内角和等于(n-2)·180?.
多边形的外角和都等于360°.
我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)×
180°。这种化未知为已知的转化方法,必须在学习中逐渐掌握。由于多边形外角和为360°,与边数无关,所以常把多边形内角和的问题转化为外角和来处理。
n-3
n-2
3×1800
4×1800
(n-2)×1800
1
2
3
2
3
4
2×1800
3600
3600
3600
3600
答:15边形的内角和是23400
12
求15边形内角和的度数。
多边形的内角和
n边形的内角和为(n-2)×1800
解:(n-2)×1800
=(15-2)×1800
=
23400
13
一个正多边形每一个内角都是120o,这个多边形是( )
A、正四边形
B、正五边形
C、正六边形
D、正七边形
C
14、镶嵌
2、任意三角形一定可以镶嵌.
4、正六边形可以镶嵌.
3、任意四边形一定可以镶嵌
注意:只用正五边形、正八边
形一种图形不能镶嵌.
1、拼接在同一个点的各个角
的和等于360度
下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;
(1)、(2)、(4)
3.如图,已知:AD是△ABC
的中线,△ABC的面积为
,求
△ABD的面积
A
B
C
D
┓
E
4.求下列图形中X的值
(3)
(2)
(1)
┛
1
D
C
A
B
A
B
C
X
1
2
3
4
7.如图,
△ABC中,
∠A=
∠ABD,
∠C=
∠BDC=
∠ABC,求∠DBC的度数
A
B
C
D
友情提示:把图形内部七边形各角看作外部三角形外角,分析可得
9、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
三角形三个内角的度数分别是(x+y)o,
(x-y)o,xo,且x>y>0,则该三角形有一个内角为
( )
A、30O
B、45O
C、60O
D、90O
把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A、只有一种截法
B、只有两种截法
C、有三种截法
D、有四种截法
等腰三角形的腰长为a,底为X,则X的取值范围是( )
A、0<X<2a
B、0<X<a
C、0<X<a/2
D、0<X≤2a
一、选择题
C
C
A
一个正多边形每一个内角都是120o,这个多边形是( )
A、正四边形
B、正五边形
C、正六边形
D、正七边形
一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为(
)
A、13条
B、14条
C、15条
D、16条
下列说法中,错误的是(
)
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
C
A
D
二、填空题
一个三角形的三边长是整数,周长为5,则最小边为
;
木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是
;
小明绕五边形各边走一圈,他共转了 度。
两多边形的边数分别是m
,n条,且各多边形内角相等,又满足1/m+1/n=1/4,则各取一外角的和为
;
下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;
1
三角形具有稳定性
360
90O
(1)、(2)、(4)
1、如图:D是△ABC中BC边上一点,
试说明2AD<AB+BC+AC。
A
C
D
B
友情提示:由AC+CD>AD与AB+BD>AD相加可得。
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
解:
由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3
5
∴
第三条边长为
7cm、9cm。
3、已知两条线段的长分别是3cm、8cm
,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长?
3、已知一个三角形的三边长3、
a+2、8,则a的取值范围是
。
3
