人教版>数学年级上册 12.3.2角平分线的性质(2)课件(22张)
文档属性
| 名称 | 人教版>数学年级上册 12.3.2角平分线的性质(2)课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
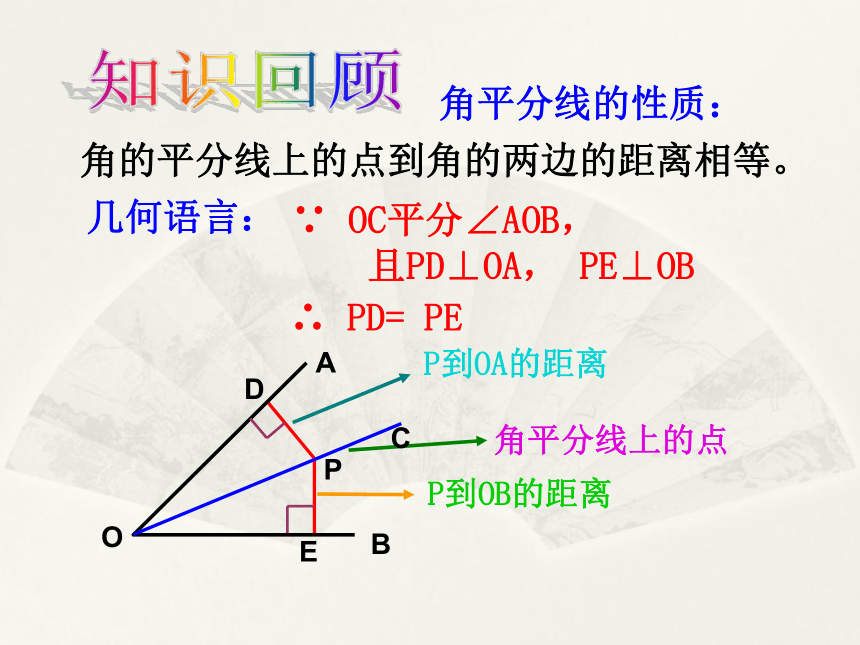
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
O
D
E
P
A
C
B
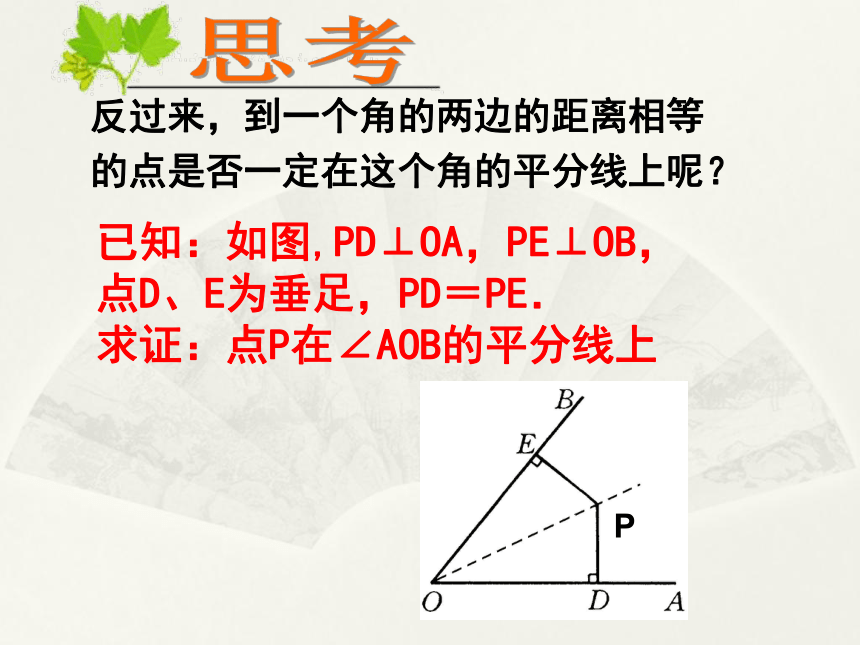
反过来,到一个角的两边的距离相等
的点是否一定在这个角的平分线上呢?
P
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
P
C
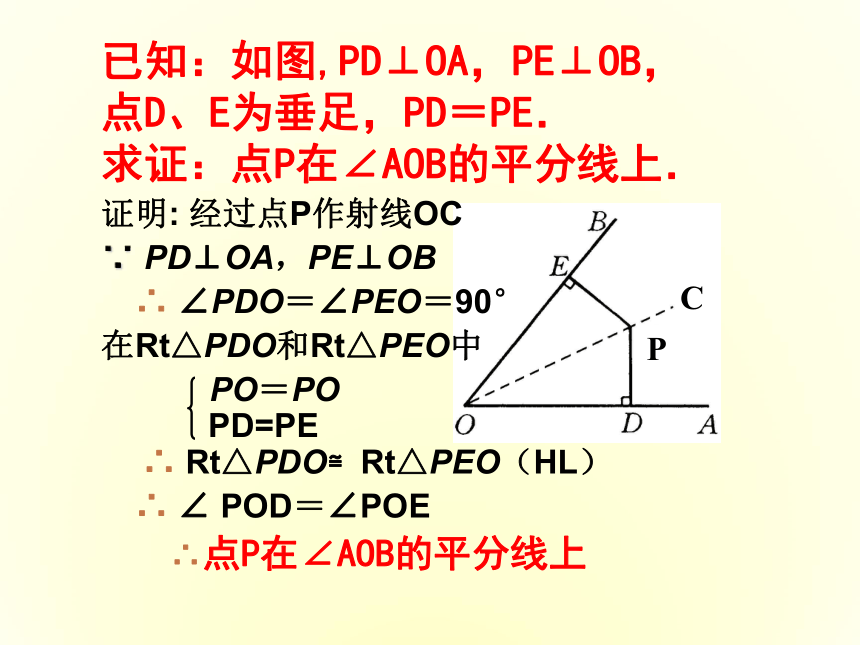
证明:
经过点P作射线OC
∵
PD⊥OA,PE⊥OB
∴
∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴
Rt△PDO≌Rt△PEO(HL)
∴
∠
POD=∠POE
∴点P在∠AOB的平分线上
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.
P
C
角的内部到角的两边的距离相等的点在角的平分线上。
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴OP平分∠AOB.
用数学语言表示为:
角平分线性质的逆定理
(角平分线的判定)
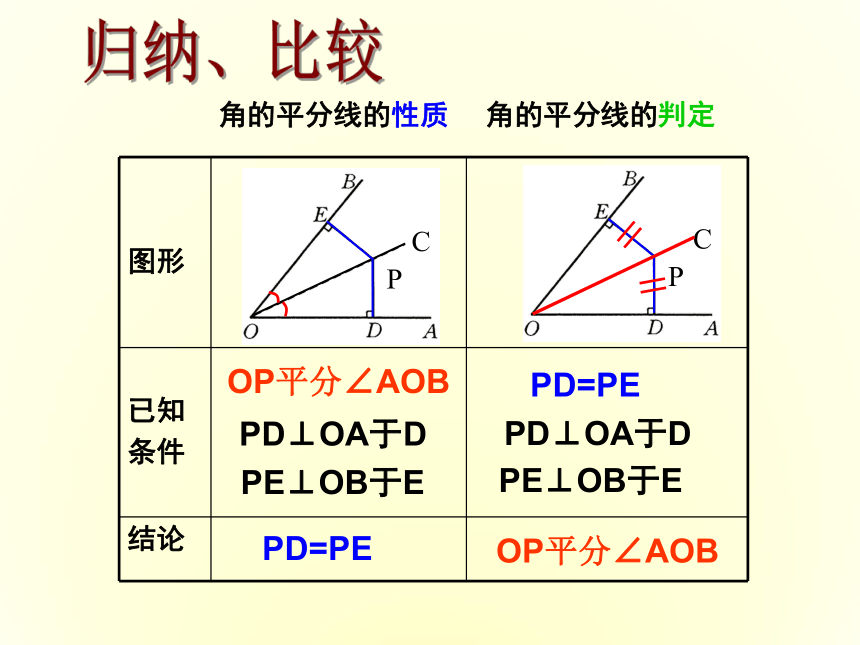
角的平分线的性质
图形
已知
条件
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
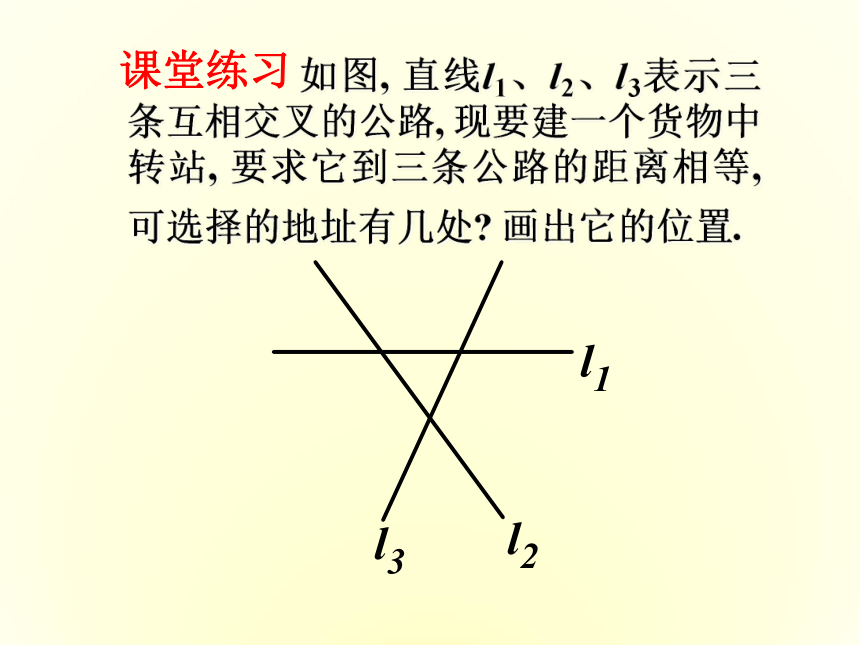
如图,
直线l1、l2、l3表示三条互相交叉的公路,
现要建一个货物中转站,
要求它到三条公路的距离相等,
可选择的地址有几处?
画出它的位置.
课堂练习
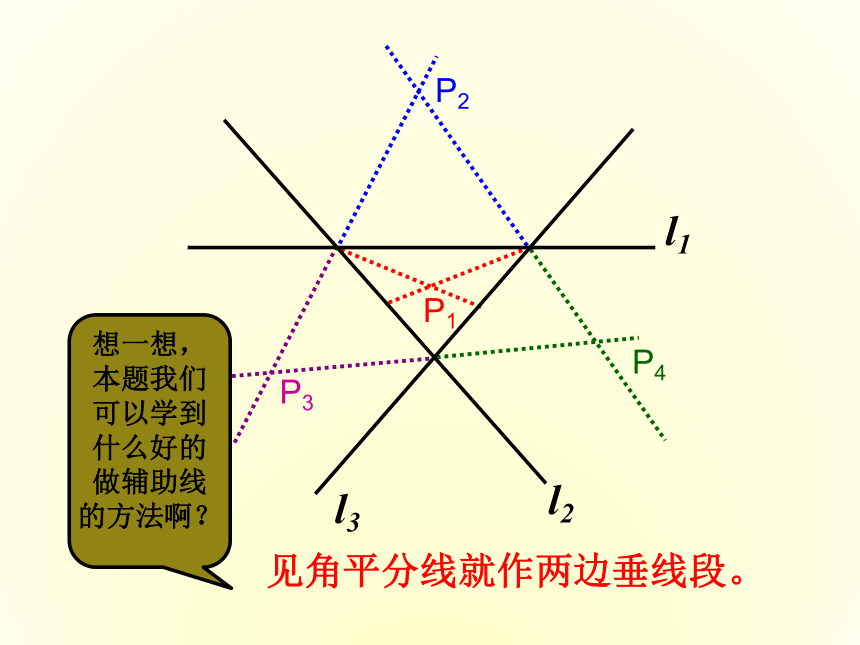
P1
P2
P3
P4
l1
l2
l3
见角平分线就作两边垂线段。
想一想,本题我们可以学到什么好的做辅助线的方法啊?
课堂练习(p51.3)
如图,CD
⊥AB,BE
⊥AC,垂足分别为D,E,BE,CD相交于点O,
OB=OC,求证
∠1=
∠2.
A
E
D
O
B
C
1
2
证明:∵
CD
⊥AB,BE
⊥AC,
∴∠BDO=∠CEO=90
°
在△BDO与△CEO中
∠BDO=∠CEO(已证)
∠BOD=∠COE(对顶角相等)
OB=OC(已知)
∴
△BDO≌△CEO(AAS)
∴OD=OE
∴O点在角平分线上(角平分线的判定定理)
∴
∠1=
∠2
课堂练习(P51.4)
如图,△ABC中,AD是它的角平分线,
P是AD
上的一点,PE∥AB,交BC于点E,
PF∥AC,交BC于点F,求证:点D到PE和PF
的距离相等。
A
C
F
D
P
E
B
今天这节课你都学了些什么?你有什么收获?
想一想:
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
1、角平分线的判定:
2、三角形角平分线的交点性质:
三角形的三条角平分线交于一点。
3、角的平分线的辅助线作法:
见角平分线就作两边垂线段。
再
见
在△ABC中,AB=AC,
AD平分∠BAC
,DE⊥AB,
DF⊥AC,
下面给出三个结论(1)DA平分∠EDF;
(2)AE=AF;(3)AD上的点到B、C两点的
距离相等,其中正确的结论有(
)
课堂练习
A
B
C
E
F
D
已知:如图,在△ABC中,
BD=CD,
∠1=
∠2.
求证:AD平分∠BAC
D
E
F
A
B
C
1
2
课堂练习
D
E
F
C
A
课堂练习
B
已知:BD⊥AC于点D,CE⊥AB于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
如图,BE⊥AC于E,
CF⊥AB于F,
BE、CF相交于D,
BD=CD
。
求证:
AD平分∠BAC
A
B
C
F
E
D
课堂练习
如图,
D,
E,
F分别是△ABC三边上的点,
CE=BF,
△DCE和△DBF的面积相等,
DH⊥AB于H,
DG⊥AC于G.
求证:
AD平分∠BAC.
课堂练习
如图,O是三条角平分线的交点,
OD⊥BC于D,OD=3,
△ABC的
周长为15,求S△ABC
A
B
C
O
M
N
G
D
课堂练习
如图,在四边形ABCD中,
∠B=∠C=90°,M是BC的中点,DM平分∠
ADC。
求证:AM平分∠DAB
D
A
B
C
M
课堂练习
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
O
D
E
P
A
C
B
反过来,到一个角的两边的距离相等
的点是否一定在这个角的平分线上呢?
P
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
P
C
证明:
经过点P作射线OC
∵
PD⊥OA,PE⊥OB
∴
∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴
Rt△PDO≌Rt△PEO(HL)
∴
∠
POD=∠POE
∴点P在∠AOB的平分线上
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.
P
C
角的内部到角的两边的距离相等的点在角的平分线上。
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴OP平分∠AOB.
用数学语言表示为:
角平分线性质的逆定理
(角平分线的判定)
角的平分线的性质
图形
已知
条件
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
如图,
直线l1、l2、l3表示三条互相交叉的公路,
现要建一个货物中转站,
要求它到三条公路的距离相等,
可选择的地址有几处?
画出它的位置.
课堂练习
P1
P2
P3
P4
l1
l2
l3
见角平分线就作两边垂线段。
想一想,本题我们可以学到什么好的做辅助线的方法啊?
课堂练习(p51.3)
如图,CD
⊥AB,BE
⊥AC,垂足分别为D,E,BE,CD相交于点O,
OB=OC,求证
∠1=
∠2.
A
E
D
O
B
C
1
2
证明:∵
CD
⊥AB,BE
⊥AC,
∴∠BDO=∠CEO=90
°
在△BDO与△CEO中
∠BDO=∠CEO(已证)
∠BOD=∠COE(对顶角相等)
OB=OC(已知)
∴
△BDO≌△CEO(AAS)
∴OD=OE
∴O点在角平分线上(角平分线的判定定理)
∴
∠1=
∠2
课堂练习(P51.4)
如图,△ABC中,AD是它的角平分线,
P是AD
上的一点,PE∥AB,交BC于点E,
PF∥AC,交BC于点F,求证:点D到PE和PF
的距离相等。
A
C
F
D
P
E
B
今天这节课你都学了些什么?你有什么收获?
想一想:
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上。
1、角平分线的判定:
2、三角形角平分线的交点性质:
三角形的三条角平分线交于一点。
3、角的平分线的辅助线作法:
见角平分线就作两边垂线段。
再
见
在△ABC中,AB=AC,
AD平分∠BAC
,DE⊥AB,
DF⊥AC,
下面给出三个结论(1)DA平分∠EDF;
(2)AE=AF;(3)AD上的点到B、C两点的
距离相等,其中正确的结论有(
)
课堂练习
A
B
C
E
F
D
已知:如图,在△ABC中,
BD=CD,
∠1=
∠2.
求证:AD平分∠BAC
D
E
F
A
B
C
1
2
课堂练习
D
E
F
C
A
课堂练习
B
已知:BD⊥AC于点D,CE⊥AB于点E,BD,CE交点F,CF=BF,
求证:点F在∠A的平分线上.
如图,BE⊥AC于E,
CF⊥AB于F,
BE、CF相交于D,
BD=CD
。
求证:
AD平分∠BAC
A
B
C
F
E
D
课堂练习
如图,
D,
E,
F分别是△ABC三边上的点,
CE=BF,
△DCE和△DBF的面积相等,
DH⊥AB于H,
DG⊥AC于G.
求证:
AD平分∠BAC.
课堂练习
如图,O是三条角平分线的交点,
OD⊥BC于D,OD=3,
△ABC的
周长为15,求S△ABC
A
B
C
O
M
N
G
D
课堂练习
如图,在四边形ABCD中,
∠B=∠C=90°,M是BC的中点,DM平分∠
ADC。
求证:AM平分∠DAB
D
A
B
C
M
课堂练习
