北师大版七年级上册数学 第三章 整式及其加减复习 课件(24张)
文档属性
| 名称 | 北师大版七年级上册数学 第三章 整式及其加减复习 课件(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 11:46:41 | ||
图片预览








文档简介
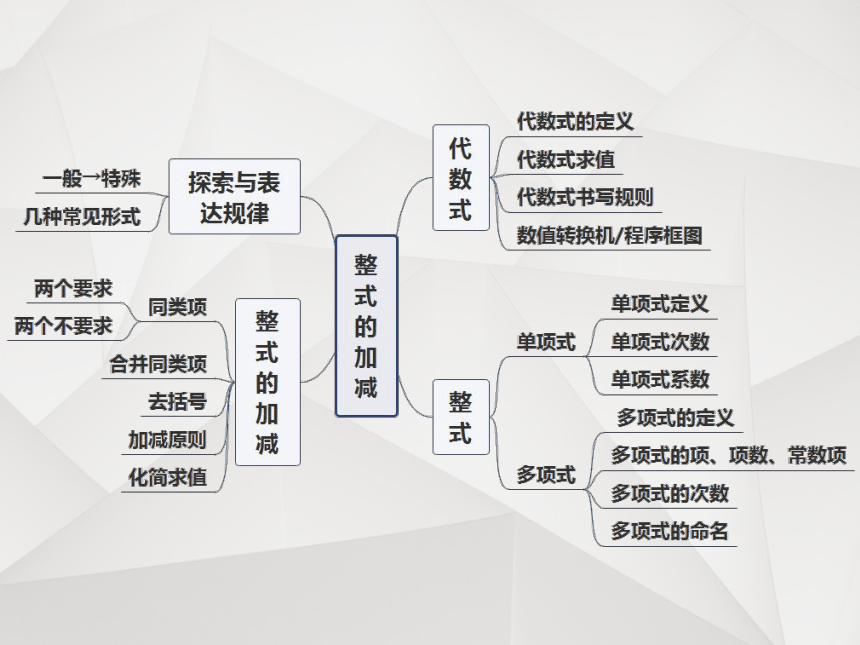
第三章《整式的加减》
复习课
教学目标
1、进一步理解代数式、单项式、多项式、整式等概念,分清它们之间的联系和区别.
2、掌握单项式系数、次数和多项式的次数、项与项数的概念,明确它们之间的关系.
3、掌握合并同类项法则和去括号规律,会熟练地进行整式的加减运算.
4、通过复习与整合,掌握全章的知识体系,进一步培养学生的计算能力,体会从特殊到一般的思想.
易错点1:书写格式
2:七(6)班有男生m人,女生比男生的一半多5人,则七(6)班的总人数为______人(用m表示)。
F
( )
1、数字与字母相乘→×省略,数字在前,字母在后
2、字母与字母相乘→×省略,顺序无要求
3、带分数与字母相乘→带分数必须换成假分数
4、出现除法运算→÷换为分数线
5、1或-1与字母相乘→“1”省略
6、多项式后面有单位,多项式需要整体带括号
7、能够化简的,必须写成最简形式
易错点2:代数式求值
3:当a=4,b=2,c=-1时,求a-bc的值。
解:a-bc=4-2×(-1)=4+2=6
注:如代入的值是负数,不要漏掉括号
4:若x2-3y-5=0,则6y-2x2-6的值为( ) A.4 B.-4 C.16 D.-16
由x2-3y-5=0可知,x2-3y=5
∴6y-2x2-6=-2(x2-3y)-6=-2×5-6=-16
D
整体代入
易错点3:概念区分
5:下列各式中,是代数式的是____________,是单项式的有_______,是多项式的是______,是整式的是_____________(填序号)。
①②④⑤⑥⑧⑨⑩
①②④⑧⑩
⑥⑨
①②④⑥⑧⑨⑩
1、代数式——区分于等式(含有=、≠)和不等式(含有<、>、≤、≥)
2、单项式:字母与字母间、数字与字母间用乘号连接(分母中不能出现字母、π是数字不是字母)
注:单独的一个数字或字母也是单项式;
3、多项式:几个单项式的和。
4、整式:单项式和多项式的统称
易错点4:定义理解
6:单项式-2.42×103π5ab6c8的次数为____,系数为________;单项式a的次数为____,系数为____;单项式-7的次数为___,系数为____.
多项式2x3-x2y2-3xy+x-1的次数为_,项数为__,组成该多项式的项有__________________,该多项式是___次___项式。
15
-2.42×103π5
1
1
0
-7
4
5
2x3,-x2y2,-3xy,x,-1
四
五
单项式的次数和系数:
1、次数=所有字母的指数之和(注意部分字母省略的1)
2、系数=去除所有字母及其指数后的剩余部分(注意数字“1”的省略与显现)
3、单独的一个数字和一个字母的系数和次数
多项式的次数、项数、项、命名:
1、多项式的次数不是所有项的次数的和,而是最高次项的次数;
2、多项式的每一项都包含它前面的符号;
3、多项式的项数等于其化为最简后所含有的单项式的个数;
4、命名:n次n项式,n=一、二、三、四,不是1、2、3、4。
8:若2a3+mb5-pa4bn+1=-7b5a4,则m+n-p=______
-4
③⑤⑥
易错点5:同类项
9:下列合并同类项的结果错误的有_________.
①②③④⑤
注意:
1、合并同类项后也要注意书写格式;
2、如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
易错点6:合并同类项
易错点7:去括号
10:判断下列各式是否正确:
√
×
×
×
1、括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2、注意外面有系数的,各项都要乘以那个系数。
易错点8:整式的加减
11:化简:3x2-[2x-3(x2-1)+2x2]
整式的加减一般步骤:
(1)有括号先去括号;(2)再合并同类项;
(3)最终结果必须为最简形式;
(4)有多重括号的,一般先去小括号,再去中括号,最后再去大括号.
部分同学的答案:
4x2+(-2x)+(-3)
(先去括号)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
易错点9:化简求值
12:化简求值:3(x2-4x+1)-(x3+4x2+6) ,其中x=-2
解:原式= 3x2-12x+3-x3-4x2-6
=-x3+3x2-4x2-12x+3-6
=-x3-x2-12x-3
原式=-(-2)3-(-2)2-12×(-2)-3
=8-4+24-3
=25
易错点10:探索与表达规律
13:用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案,则第10个图案中有白色地面砖______块.
(4n+2)
x2
an
(-1)n+1
综合解析
例:关于x,y的代数式
x4+ax3+3y2+5x3-(7y2+by2-6x)-2
(1)此代数式不含有x3,y2项,求2a+3b的值;
(2)此代数式为四次三项式,求2a+3b的值;
(3)此代数式的值与y的取值无关,求-b2的值。
(x,y为字母)
步骤:
1、去括号,合并同类项;
2、根据题意,使对应项系数为0;
3、代入求值。
解:原式=x4+ax3+3y2+5x3-7y2-by2+6x-2
=x4+ax3+5x3+3y2-7y2-by2+6x-2
=x4+(a+5)x3+(3-7-b)y2+6x-2
= x4+(a+5)x3-(4+b)y2+6x-2
(1)∵代数式不含有x3,y2项
∴a+5=0,4+b=0
∴a=-5,b=-4
将a=-5,b=-4代入2a+3b得
2a+3b=2×(-5)+3×(-4)=-22
去括号
合并同类项
根据题目要求求参数值
代入求值
(3)∵代数式的值与y的取值无关
∴4+b=0
∴b=-4
(2)∵代数式为四次三项式
∴a+5=0,4+b=0
∴a=-5,b=-4
将a=-5,b=-4代入2a+3b得
2a+3b=2×(-5)+3×(-4)=-22
根据题目要求求参数值
代入求值
x4+(a+5)x3-(4+b)y2+6x-2
根据题目要求求参数值
代入求值
将b=-4代入-b2得
-b2=-(-4)2=-16
复习课
教学目标
1、进一步理解代数式、单项式、多项式、整式等概念,分清它们之间的联系和区别.
2、掌握单项式系数、次数和多项式的次数、项与项数的概念,明确它们之间的关系.
3、掌握合并同类项法则和去括号规律,会熟练地进行整式的加减运算.
4、通过复习与整合,掌握全章的知识体系,进一步培养学生的计算能力,体会从特殊到一般的思想.
易错点1:书写格式
2:七(6)班有男生m人,女生比男生的一半多5人,则七(6)班的总人数为______人(用m表示)。
F
( )
1、数字与字母相乘→×省略,数字在前,字母在后
2、字母与字母相乘→×省略,顺序无要求
3、带分数与字母相乘→带分数必须换成假分数
4、出现除法运算→÷换为分数线
5、1或-1与字母相乘→“1”省略
6、多项式后面有单位,多项式需要整体带括号
7、能够化简的,必须写成最简形式
易错点2:代数式求值
3:当a=4,b=2,c=-1时,求a-bc的值。
解:a-bc=4-2×(-1)=4+2=6
注:如代入的值是负数,不要漏掉括号
4:若x2-3y-5=0,则6y-2x2-6的值为( ) A.4 B.-4 C.16 D.-16
由x2-3y-5=0可知,x2-3y=5
∴6y-2x2-6=-2(x2-3y)-6=-2×5-6=-16
D
整体代入
易错点3:概念区分
5:下列各式中,是代数式的是____________,是单项式的有_______,是多项式的是______,是整式的是_____________(填序号)。
①②④⑤⑥⑧⑨⑩
①②④⑧⑩
⑥⑨
①②④⑥⑧⑨⑩
1、代数式——区分于等式(含有=、≠)和不等式(含有<、>、≤、≥)
2、单项式:字母与字母间、数字与字母间用乘号连接(分母中不能出现字母、π是数字不是字母)
注:单独的一个数字或字母也是单项式;
3、多项式:几个单项式的和。
4、整式:单项式和多项式的统称
易错点4:定义理解
6:单项式-2.42×103π5ab6c8的次数为____,系数为________;单项式a的次数为____,系数为____;单项式-7的次数为___,系数为____.
多项式2x3-x2y2-3xy+x-1的次数为_,项数为__,组成该多项式的项有__________________,该多项式是___次___项式。
15
-2.42×103π5
1
1
0
-7
4
5
2x3,-x2y2,-3xy,x,-1
四
五
单项式的次数和系数:
1、次数=所有字母的指数之和(注意部分字母省略的1)
2、系数=去除所有字母及其指数后的剩余部分(注意数字“1”的省略与显现)
3、单独的一个数字和一个字母的系数和次数
多项式的次数、项数、项、命名:
1、多项式的次数不是所有项的次数的和,而是最高次项的次数;
2、多项式的每一项都包含它前面的符号;
3、多项式的项数等于其化为最简后所含有的单项式的个数;
4、命名:n次n项式,n=一、二、三、四,不是1、2、3、4。
8:若2a3+mb5-pa4bn+1=-7b5a4,则m+n-p=______
-4
③⑤⑥
易错点5:同类项
9:下列合并同类项的结果错误的有_________.
①②③④⑤
注意:
1、合并同类项后也要注意书写格式;
2、如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
易错点6:合并同类项
易错点7:去括号
10:判断下列各式是否正确:
√
×
×
×
1、括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2、注意外面有系数的,各项都要乘以那个系数。
易错点8:整式的加减
11:化简:3x2-[2x-3(x2-1)+2x2]
整式的加减一般步骤:
(1)有括号先去括号;(2)再合并同类项;
(3)最终结果必须为最简形式;
(4)有多重括号的,一般先去小括号,再去中括号,最后再去大括号.
部分同学的答案:
4x2+(-2x)+(-3)
(先去括号)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
易错点9:化简求值
12:化简求值:3(x2-4x+1)-(x3+4x2+6) ,其中x=-2
解:原式= 3x2-12x+3-x3-4x2-6
=-x3+3x2-4x2-12x+3-6
=-x3-x2-12x-3
原式=-(-2)3-(-2)2-12×(-2)-3
=8-4+24-3
=25
易错点10:探索与表达规律
13:用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案,则第10个图案中有白色地面砖______块.
(4n+2)
x2
an
(-1)n+1
综合解析
例:关于x,y的代数式
x4+ax3+3y2+5x3-(7y2+by2-6x)-2
(1)此代数式不含有x3,y2项,求2a+3b的值;
(2)此代数式为四次三项式,求2a+3b的值;
(3)此代数式的值与y的取值无关,求-b2的值。
(x,y为字母)
步骤:
1、去括号,合并同类项;
2、根据题意,使对应项系数为0;
3、代入求值。
解:原式=x4+ax3+3y2+5x3-7y2-by2+6x-2
=x4+ax3+5x3+3y2-7y2-by2+6x-2
=x4+(a+5)x3+(3-7-b)y2+6x-2
= x4+(a+5)x3-(4+b)y2+6x-2
(1)∵代数式不含有x3,y2项
∴a+5=0,4+b=0
∴a=-5,b=-4
将a=-5,b=-4代入2a+3b得
2a+3b=2×(-5)+3×(-4)=-22
去括号
合并同类项
根据题目要求求参数值
代入求值
(3)∵代数式的值与y的取值无关
∴4+b=0
∴b=-4
(2)∵代数式为四次三项式
∴a+5=0,4+b=0
∴a=-5,b=-4
将a=-5,b=-4代入2a+3b得
2a+3b=2×(-5)+3×(-4)=-22
根据题目要求求参数值
代入求值
x4+(a+5)x3-(4+b)y2+6x-2
根据题目要求求参数值
代入求值
将b=-4代入-b2得
-b2=-(-4)2=-16
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
