2020_2021学年新教材高中数学第十章概率10.2事件的相互独立性课件(共30张PPT)新人教A版必修第二册
文档属性
| 名称 | 2020_2021学年新教材高中数学第十章概率10.2事件的相互独立性课件(共30张PPT)新人教A版必修第二册 |

|
|
| 格式 | zip | ||
| 文件大小 | 866.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 07:26:54 | ||
图片预览











文档简介
(共30张PPT)
10.2 事件的相互独立性
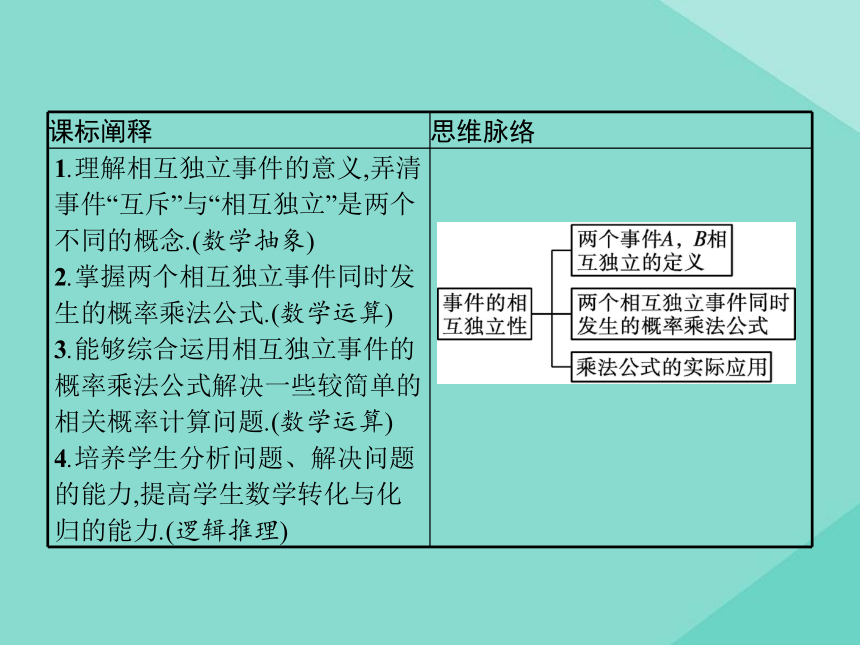
课标阐释
思维脉络
1.理解相互独立事件的意义,弄清事件“互斥”与“相互独立”是两个不同的概念.(数学抽象)
2.掌握两个相互独立事件同时发生的概率乘法公式.(数学运算)
3.能够综合运用相互独立事件的概率乘法公式解决一些较简单的相关概率计算问题.(数学运算)
4.培养学生分析问题、解决问题的能力,提高学生数学转化与化归的能力.(逻辑推理)
激趣诱思
知识点拨
问题一:“常言道,三个臭皮匠能抵诸葛亮.”怎样从数学上来解释呢?将问题具体化:假如对某事件诸葛亮想出计谋的概率为0.88,三个臭皮匠甲、乙、丙想出计谋的概率各为0.6、0.5、0.5.问这三个臭皮匠能胜过诸葛亮吗?
问题二:
2010年1月26日上午,NBA常规赛进行了一场焦点之战——勒布朗·詹姆斯领衔的克利夫兰骑士在客场挑战由韦德率领的迈阿密热火.比赛非常激烈,直到终场前3.1秒比分打成90平,热火队犯规,詹姆斯获两次罚篮机会,已知詹姆斯的罚篮命中率为77.6%,问骑士队此时获胜的概率是多少?
激趣诱思
知识点拨
知识点一、两个事件相互独立
对任意两个事件A与B,如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立.
名师点析
(1)如果A与B相互独立,那么A与
也都相互独立.(2)必然事件Ω、不可能事件?都与任意事件相互独立.因为必然事件Ω总会发生,不会受任何事件是否发生的影响,不可能事件?总不会发生,也不受任何事件是否发生的影响.当然,它们也不影响其他事件是否发生.(3)对于n个事件A1,A2,…,An,如果其中任意一个事件发生的概率不受其他事件是否发生的影响,则称n个事件A1,A2,…,An相互独立.
激趣诱思
知识点拨
微思考
分别抛掷两枚质地均匀的硬币,事件A=“第一枚硬币正面朝上”,事件B=“第二枚硬币反面朝上”.你觉得事件A发生与否会影响事件B的发生吗?P(A),P(B)与P(AB)有怎样的关系?
激趣诱思
知识点拨
微练习
若事件A与B相互独立,则下面的事件不相互独立的是( )
答案:A
激趣诱思
知识点拨
知识点二、两个相互独立事件同时发生的概率乘法公式
若A,B是两个相互独立事件,则有P(AB)=P(A)P(B)成立.
名师点析
(1)三个事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)成立.但三个事件A,B,C两两独立时,等式P(ABC)=P(A)P(B)P(C)一般不成立.
(2)A,B,C相互独立的充要条件是:P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(CA)=P(C)P(A),
P(ABC)=P(A)P(B)·P(C),4个条件每个都必不可少.
激趣诱思
知识点拨
微思考
如果连续10次掷一枚骰子,结果都是出现1点,你认为这枚骰子的质地均匀吗?为什么?
提示:可以推测这枚骰子的质地不均匀,并且很有可能是标有6点的那面比较重,使得出现1点的概率最大,才会连续10次都出现1点.
激趣诱思
知识点拨
微练习
若事件E与F相互独立,且P(E)=P(F)=
,则P(EF)的值等于( )
答案:B
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件的判断
例1抛掷一枚均匀的骰子一次,记事件A=“出现偶数点”,B=“出现3点或6点”,则事件A与B的关系是( )
A.互斥
B.相互独立
C.既互斥又相互独立
D.既不互斥又不相互独立
解析:因为A={2,4,6},B={3,6},A∩B={6},
答案:B
反思感悟
判断两个事件A,B是否相互独立,一般有两种思路,一种是直接法,即从是否相互影响其发生(偏感性认识)判断;第二种是定义法,即利用定义P(AB)=P(A)P(B)进行理性判断.
探究一
探究二
探究三
素养形成
当堂检测
变式训练1袋内有3个白球和2个黑球,从中不放回地摸球,记A=“第一次摸的白球”,B=“第二次摸的白球”,则A与B( )
A.互斥
B.相互独立
C.对立
D.不相互独立
答案:D
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件和互斥事件的概率问题
例2已知甲袋中装有大小、形状、质地相同的3个白球和2个红球,乙袋中装有1个白球和4个红球.现从甲、乙两袋中各摸一个球,试求:
(1)两球都是红球的概率;
(2)恰有一个是红球的概率;
(3)至少有一个是红球的概率.
分析判断基本事件的构成,及各事件间的关系,选择合适的公式计算.
探究一
探究二
探究三
素养形成
当堂检测
解:记事件A表示“从甲袋中摸出一个红球”,事件B表示“从乙袋中摸出一个红球”,事件C表示“从甲、乙两袋中各摸一个球,恰好摸出一个红球”,事件D表示“至少摸出一个红球”.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求复杂事件的概率,应先列出题中涉及的各事件,并用适当的符号表示,再理清各事件之间的关系,最后根据事件之间的关系选取相应的公式进行计算.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2甲、乙两人独立地破译一个密码,他们能译出密码的概率分别为
(1)2人都译不出密码的概率;
(2)恰有1人译出密码的概率;
(3)至多有1人译出密码的概率;
(4)至少有1人译出密码的概率.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件同时发生的概率
例3某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为
,且各轮问题能否正确回答互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率.
分析把所求事件分解成几个独立事件或互斥事件.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求相互独立事件同时发生的概率时,可运用公式P(AB)=P(A)P(B).在解决问题时,要搞清事件是否独立,把复杂事件分解为若干简单事件来处理,同时还要注意运用对立事件把问题简单化.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3
如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作.已知K,A1,A2正常工作的概率依次为0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960
B.0.864
C.0.720
D.0.576
探究一
探究二
探究三
素养形成
当堂检测
答案:B
探究一
探究二
探究三
素养形成
当堂检测
概率问题中的数学思想
典例在一段线路中并联着3个自动控制的常开开关,只要其中有1个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关闭合的概率都是0.7,计算在这段时间内线路正常工作的概率.
分析该线路是并联电路,当且仅当三个开关都不闭合时,线路才不通,故本题可采用对立事件求解.
探究一
探究二
探究三
素养形成
当堂检测
解:分别记这段时间内开关JA,JB,JC能够闭合为事件A,B,C.由题意知,这段时间内3个开关是否能够闭合相互之间没有影响.根据相互独立事件概率的乘法公式,得这段时间内3个开关都不能闭合的概率
探究一
探究二
探究三
素养形成
当堂检测
方法点睛
概率问题中的数学思想
(1)正难则反.灵活应用对立事件的概率关系(P(A)+P(
)=1)简化问题,是求解概率问题最常用的方法.
(2)化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.弄清“所求事件”是分几类(考虑加法公式,转化为互斥事件)还是分几步(考虑乘法公式,转化为相互独立事件).
(3)方程思想.利用有关的概率公式和问题中的数量关系,建立方程(组),通过解方程(组)使问题获解.
探究一
探究二
探究三
素养形成
当堂检测
答案:B
探究一
探究二
探究三
素养形成
当堂检测
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.一件产品要经过2道独立的加工程序,第一道工序的次品率为a,第二道工序的次品率为b,则产品的正品率为( )
A.1-a-b
B.1-ab
C.(1-a)(1-b)
D.1-(1-a)(1-b)
解析:设A表示“第一道工序的产品为正品”,B表示“第二道工序的产品为正品”,且P(AB)=P(A)P(B)=(1-a)(1-b).
答案:C
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
5.某天上午,李明要参加“青年文明号”活动.为了准时起床,他用甲、乙两个闹钟叫醒自己.假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一个准时响的概率是 .?
解析:至少有一个准时响的概率为1-(1-0.90)×(1-0.80)
=1-0.10×0.20=0.98.
答案:0.98
10.2 事件的相互独立性
课标阐释
思维脉络
1.理解相互独立事件的意义,弄清事件“互斥”与“相互独立”是两个不同的概念.(数学抽象)
2.掌握两个相互独立事件同时发生的概率乘法公式.(数学运算)
3.能够综合运用相互独立事件的概率乘法公式解决一些较简单的相关概率计算问题.(数学运算)
4.培养学生分析问题、解决问题的能力,提高学生数学转化与化归的能力.(逻辑推理)
激趣诱思
知识点拨
问题一:“常言道,三个臭皮匠能抵诸葛亮.”怎样从数学上来解释呢?将问题具体化:假如对某事件诸葛亮想出计谋的概率为0.88,三个臭皮匠甲、乙、丙想出计谋的概率各为0.6、0.5、0.5.问这三个臭皮匠能胜过诸葛亮吗?
问题二:
2010年1月26日上午,NBA常规赛进行了一场焦点之战——勒布朗·詹姆斯领衔的克利夫兰骑士在客场挑战由韦德率领的迈阿密热火.比赛非常激烈,直到终场前3.1秒比分打成90平,热火队犯规,詹姆斯获两次罚篮机会,已知詹姆斯的罚篮命中率为77.6%,问骑士队此时获胜的概率是多少?
激趣诱思
知识点拨
知识点一、两个事件相互独立
对任意两个事件A与B,如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立.
名师点析
(1)如果A与B相互独立,那么A与
也都相互独立.(2)必然事件Ω、不可能事件?都与任意事件相互独立.因为必然事件Ω总会发生,不会受任何事件是否发生的影响,不可能事件?总不会发生,也不受任何事件是否发生的影响.当然,它们也不影响其他事件是否发生.(3)对于n个事件A1,A2,…,An,如果其中任意一个事件发生的概率不受其他事件是否发生的影响,则称n个事件A1,A2,…,An相互独立.
激趣诱思
知识点拨
微思考
分别抛掷两枚质地均匀的硬币,事件A=“第一枚硬币正面朝上”,事件B=“第二枚硬币反面朝上”.你觉得事件A发生与否会影响事件B的发生吗?P(A),P(B)与P(AB)有怎样的关系?
激趣诱思
知识点拨
微练习
若事件A与B相互独立,则下面的事件不相互独立的是( )
答案:A
激趣诱思
知识点拨
知识点二、两个相互独立事件同时发生的概率乘法公式
若A,B是两个相互独立事件,则有P(AB)=P(A)P(B)成立.
名师点析
(1)三个事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)成立.但三个事件A,B,C两两独立时,等式P(ABC)=P(A)P(B)P(C)一般不成立.
(2)A,B,C相互独立的充要条件是:P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(CA)=P(C)P(A),
P(ABC)=P(A)P(B)·P(C),4个条件每个都必不可少.
激趣诱思
知识点拨
微思考
如果连续10次掷一枚骰子,结果都是出现1点,你认为这枚骰子的质地均匀吗?为什么?
提示:可以推测这枚骰子的质地不均匀,并且很有可能是标有6点的那面比较重,使得出现1点的概率最大,才会连续10次都出现1点.
激趣诱思
知识点拨
微练习
若事件E与F相互独立,且P(E)=P(F)=
,则P(EF)的值等于( )
答案:B
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件的判断
例1抛掷一枚均匀的骰子一次,记事件A=“出现偶数点”,B=“出现3点或6点”,则事件A与B的关系是( )
A.互斥
B.相互独立
C.既互斥又相互独立
D.既不互斥又不相互独立
解析:因为A={2,4,6},B={3,6},A∩B={6},
答案:B
反思感悟
判断两个事件A,B是否相互独立,一般有两种思路,一种是直接法,即从是否相互影响其发生(偏感性认识)判断;第二种是定义法,即利用定义P(AB)=P(A)P(B)进行理性判断.
探究一
探究二
探究三
素养形成
当堂检测
变式训练1袋内有3个白球和2个黑球,从中不放回地摸球,记A=“第一次摸的白球”,B=“第二次摸的白球”,则A与B( )
A.互斥
B.相互独立
C.对立
D.不相互独立
答案:D
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件和互斥事件的概率问题
例2已知甲袋中装有大小、形状、质地相同的3个白球和2个红球,乙袋中装有1个白球和4个红球.现从甲、乙两袋中各摸一个球,试求:
(1)两球都是红球的概率;
(2)恰有一个是红球的概率;
(3)至少有一个是红球的概率.
分析判断基本事件的构成,及各事件间的关系,选择合适的公式计算.
探究一
探究二
探究三
素养形成
当堂检测
解:记事件A表示“从甲袋中摸出一个红球”,事件B表示“从乙袋中摸出一个红球”,事件C表示“从甲、乙两袋中各摸一个球,恰好摸出一个红球”,事件D表示“至少摸出一个红球”.
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求复杂事件的概率,应先列出题中涉及的各事件,并用适当的符号表示,再理清各事件之间的关系,最后根据事件之间的关系选取相应的公式进行计算.
探究一
探究二
探究三
素养形成
当堂检测
变式训练2甲、乙两人独立地破译一个密码,他们能译出密码的概率分别为
(1)2人都译不出密码的概率;
(2)恰有1人译出密码的概率;
(3)至多有1人译出密码的概率;
(4)至少有1人译出密码的概率.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
相互独立事件同时发生的概率
例3某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为
,且各轮问题能否正确回答互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率.
分析把所求事件分解成几个独立事件或互斥事件.
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
反思感悟
求相互独立事件同时发生的概率时,可运用公式P(AB)=P(A)P(B).在解决问题时,要搞清事件是否独立,把复杂事件分解为若干简单事件来处理,同时还要注意运用对立事件把问题简单化.
探究一
探究二
探究三
素养形成
当堂检测
变式训练3
如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作.已知K,A1,A2正常工作的概率依次为0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960
B.0.864
C.0.720
D.0.576
探究一
探究二
探究三
素养形成
当堂检测
答案:B
探究一
探究二
探究三
素养形成
当堂检测
概率问题中的数学思想
典例在一段线路中并联着3个自动控制的常开开关,只要其中有1个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关闭合的概率都是0.7,计算在这段时间内线路正常工作的概率.
分析该线路是并联电路,当且仅当三个开关都不闭合时,线路才不通,故本题可采用对立事件求解.
探究一
探究二
探究三
素养形成
当堂检测
解:分别记这段时间内开关JA,JB,JC能够闭合为事件A,B,C.由题意知,这段时间内3个开关是否能够闭合相互之间没有影响.根据相互独立事件概率的乘法公式,得这段时间内3个开关都不能闭合的概率
探究一
探究二
探究三
素养形成
当堂检测
方法点睛
概率问题中的数学思想
(1)正难则反.灵活应用对立事件的概率关系(P(A)+P(
)=1)简化问题,是求解概率问题最常用的方法.
(2)化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.弄清“所求事件”是分几类(考虑加法公式,转化为互斥事件)还是分几步(考虑乘法公式,转化为相互独立事件).
(3)方程思想.利用有关的概率公式和问题中的数量关系,建立方程(组),通过解方程(组)使问题获解.
探究一
探究二
探究三
素养形成
当堂检测
答案:B
探究一
探究二
探究三
素养形成
当堂检测
答案:C
探究一
探究二
探究三
素养形成
当堂检测
3.一件产品要经过2道独立的加工程序,第一道工序的次品率为a,第二道工序的次品率为b,则产品的正品率为( )
A.1-a-b
B.1-ab
C.(1-a)(1-b)
D.1-(1-a)(1-b)
解析:设A表示“第一道工序的产品为正品”,B表示“第二道工序的产品为正品”,且P(AB)=P(A)P(B)=(1-a)(1-b).
答案:C
探究一
探究二
探究三
素养形成
当堂检测
探究一
探究二
探究三
素养形成
当堂检测
5.某天上午,李明要参加“青年文明号”活动.为了准时起床,他用甲、乙两个闹钟叫醒自己.假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一个准时响的概率是 .?
解析:至少有一个准时响的概率为1-(1-0.90)×(1-0.80)
=1-0.10×0.20=0.98.
答案:0.98
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
