新版湘教版八年级数学上册 2.1三角形课件(共71张PPT)
文档属性
| 名称 | 新版湘教版八年级数学上册 2.1三角形课件(共71张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 08:48:02 | ||
图片预览










文档简介
(共71张PPT)
从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形状?
在我们的生活中有没有这样的形状?能举例子吗?
三角形(1)
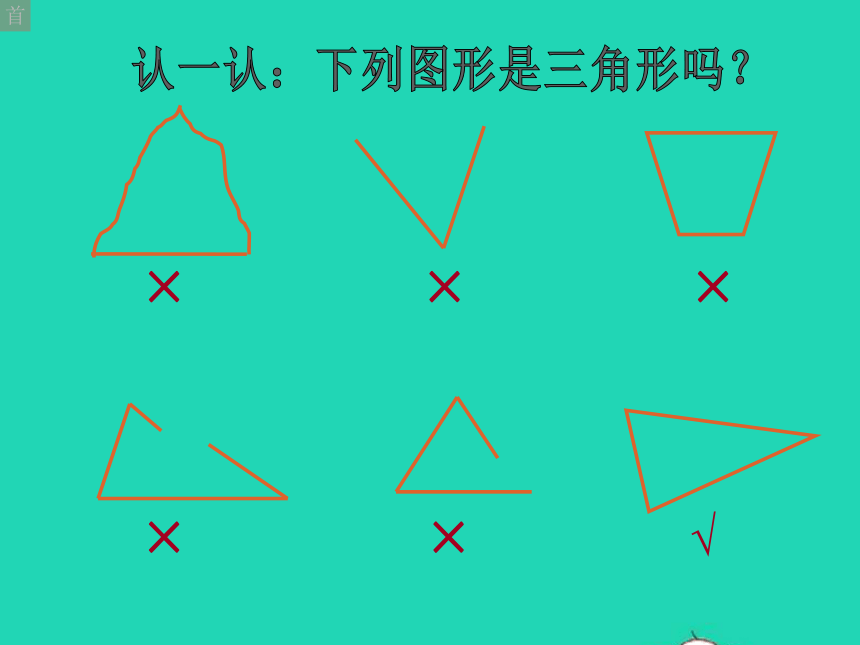
认识三角形
定义:不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
一.三角形的定义
×
×
×
√
×
×
首
1、顶点:
用一个大写字母表示如A、B、C
2、边:
边AB,边BC,边AC
3、角(内角):
相邻两边
的夹角
∠A,∠B,∠C
4、三角形记作:△ABC
A
B
C
5、对角:
对边:
∠C的对边是BA
BC边的对角是∠A
二.三角形的相关概念
A
B
C
在△ABC中
a
b
c
D
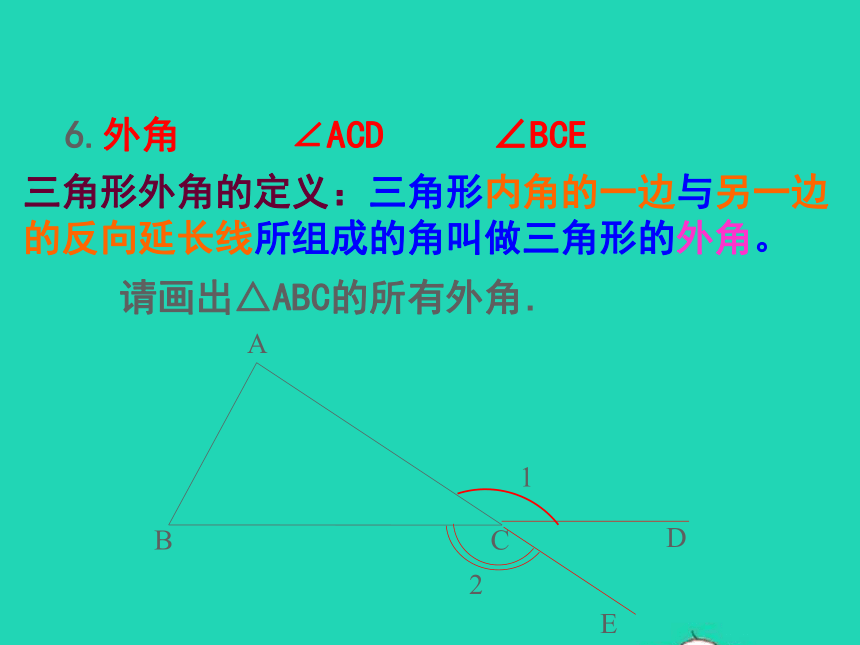
三角形外角的定义:三角形内角的一边与另一边
的反向延长线所组成的角叫做三角形的外角。
B
A
C
1
2
E
6.外角
∠ACD
∠BCE
请画出△ABC的所有外角.
.
.
.
所有外角
3
(
(
2
(
1
(
4
(
5
(
6
例:下图中有几个三角形?并把它们表示出来
指出△ADC的三个内角、三条边
A
B
C
D
(1)∠ADC能写成∠D吗?∠ACD能写成∠C吗?为什么?
(2)有人说CD是△ACD和△BCD的公共的边,对吗?AD是△ACD和△ABD的公共边,对吗?
(3)∠BDC是△BCD的什么角?
提问
例、图中以BC为边的三角形共有______个;它们分别______________________________.
在△ABD中,∠A是_______边的对角,
∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF;
△
BCE;
△
BCD;
△
BCA
△FDC
或△BDC
ABD
BD
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形(不规则三角形)
等腰三角形
三.三角形的分类
只有两条边相等的等腰三角形
等边三角形
斜三角形
说出你所知道的各种三角形的名称
等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
不等边三角形
a
c
b
a
a
a
a
a
b
等腰三角形中,相等的边叫腰,另一边叫底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
底
腰
腰
顶角
底角
底角
等腰三角形和等边三角形为特殊的三角形
1.图中有几个三角形?
用符号表示这些三角形。
A
B
C
D
E
△ABE
△BEC
△DEC
△ABC
△DBC
注:表示三角形时,字母没有先后顺序;
四.练习
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE
4.说出其中ΔBCD的三个角?
∠BCD
、
∠CBD
、∠D
A
B
C
D
E
l、三角形的概念,一个三角形有三个顶点,三条边,三个内角,六个外角,和三角形一个内角相邻的外角有2个,它们是对顶角,若一个顶点只取一个外角,那么只有3个外角。
五.知识巩固
2.三角形的分类:按角分为三类:①锐角三角形,②直角三角形,③钝角三角形。按边分为三类:①三边都不相等的三角形;②等腰三角形。
等边三角形只是等腰三角形中的一种特殊的三角形。
2.掌握了三角形的基本要素及其表示法;
3.学会对三角形进行合理分类,并了解
分类的基本原理;
4、学会用数学知识进行说理.
1、本节通过贴近我们生活的图片出发,体验了三角形知识的产生过程;
六.课堂总结
知识背景
1.
叫做三角形
由不在同一条直线上的三条线段首尾顺次相接所组成的图形
2.
三角形边的性质:
三角形任何两边的和大于第三边
三角形任何两边的差小于第三边
3.
角的分类:
锐角
(小于直角的角)
直角
(等于90°的角)
钝角
(大于直角而小于平角的角)
平角
(等于180°的角)
周角
(等于360°的角)
∠A+∠B+∠C=180°
即三角形三个内角的和等于180°
你能用其他方法得到相同的发现吗?
自主发现
例1
:
在△ABC中,如图,已知∠A=45°,∠B=30°,求∠C的度数。
A
C
B
变式1:在△
ABC中,∠A=45°,∠B=
2∠C,求∠B、
∠C的度数。
变式2:在△
ABC中,∠A=∠B=2∠C,求∠B、
∠C的度数。
三角形可以按内角的大小进行分类:
三角形
锐角三角形
(acute
triangle)
三个内角都是锐角
A
C
B
直角三角形
(right
triangle)
有一个内角是直角
A
C
B
钝角三角形
(obtuse
triangle)
有一个内角是钝角
A
C
B
(1)
在三角形中,最多有几个锐角?几个钝角?几个直角呢?
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
将下面的这些三角形进行分类:
?
请你判断
?
1.
如果
的两内角互余,则
按角分类是
三角形
ABC
ABC
直角
ABC
2.
若∠A=72°,∠B=41°,则
按角分类是
三角形
锐角
ABC
3.
若∠A+∠B=∠C,则
按角分类是
三角形
直角
4.
对于三角形的内角,下列判断不正确的是(
)
A.至少有两个锐角
B.最多有一个直角
C.必有一个角大于60°
D.至少有一个角不小于60°
C
与三角形的内角直接相关的
一个概念是三角形的外角。
A
B
C
D
如图,∠ACD由
一
条边BC的延长线和另一
条相邻的边AC组成的角,
叫做该三角形的
外角(exterior
angle)
ABC
(2)
A
B
C
D
如图,∠ACD是
一外角.
ABC
(1)你能通过延长各边,将
的所有的外角表示出来吗?
一个三角形有多少个外角?
ABC
(2)外角∠ACD与两个和它不相
邻的内角有什么关系?
请与
你的同伴交流一下.
三角形的一个外角等于和它不相邻的两个内角的和
梳理知识
三角形的一个外角等于和
它不相邻的两个内角的和
A
B
C
D
ABC
在
中,
∠ACD是
一外角.
ABC
你能结合图形用数学式子来表示吗?
∠ACD=∠A+∠B
你能用学过的知识加以解释吗?
∵∠A+∠B+∠ACB=180°
又∵∠ACB+∠ACD=180°
∴
∠ACD=∠A+∠B
?
?
巩固练习
A
B
C
D
(1)若∠A=74°,∠B=42°,
则∠ACD=
.
(2)若∠ACD=114
°36′,
∠A=65°,则∠B=
.
116°
49°36′
ABC
在
中,
如图,
∠ACD是
外角.
ABC
1.
2.在下面这幅埃及金字塔图中,三角形有两个内角相等,相等内角的一个外角等于135°,求图中三角形的各内角的度数。
135°
A
B
C
D
解:
∵∠ACB+∠ACD=180°
∠ACD=135°
∴∠ACB=180°-135°=45°
∴∠B=∠ACB=45°
又∵∠A+∠B+∠ACB=180°
∴∠A=180°-(∠A+∠B)=90°
①三角形的一个外角等于其它不相邻的两个内角和;
②三角形的一个外角,大于任何一个和它不相邻的内角.
A
B
C
D
例2:一把椅子的结构如图,
∠1=∠2当椅面水平时,
∠3=100°,此时∠1的度数是多少?
1
2
3
1
2
3
解:
∵
∠3是△ABC的一个外角
∴∠3=
∠1+∠2
(三角形的一个外角等于和它不相邻的两个内角的和)
∵
∠1=∠2
∴
∠3=
2∠1
∴
∠1=
∠2
=
1/2∠3=1/2×100
°
=50
°
A
B
C
课堂达标
1.
三角形按角分类,可以分为
三角形,
三角形,
三角形
锐角
直角
钝角
ABC
2.在
中,
(1)若∠A=54°,∠B=27°,则∠C=
.
99°
(2)若∠B=∠C=30°,则∠A=
,
为
三角形
ABC
120°
钝角
(3)若∠A:∠B:∠C=1:2:3,则∠A=
,∠B=
,∠C
=
.
30°
60°
90°
ABC
3.
如图,在Rt
中,∠ACB=90°,CD⊥AB,垂足为D,则可
以推得∠ACD=∠B.试把下面的推理过程填写完整:
A
C
D
B
解:
∵∠ACB=90°(
已知
)
∴∠ACD+∠BCD=
.
∵CD⊥AB
(
)
∴∠CDB=∠ADC=90°
∴∠B+∠BCD
=∠ADC=90°(
)
∴∠ACD=∠B
已知
三角形的一个外角等于和它不相邻的两个内角的和
90°
例3.已知如图:∠BAF、∠CBD、
∠ACE是△ABC的三个外角。
说明:∠BAF+∠CBD+∠ACE=3600
E
A
F
B
D
C
1
2
3
证明:如图,
A
B
D
C
1
2
3
F
∠BAF=∠2+∠3,
∠CBD=∠1+∠3,
∠ACE=∠1+∠2
(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠BAF+∠CBD+∠ACE
=(∠2+∠3+∠1+∠3+∠1+∠2)
=2(∠1+∠2+∠3)
例4 已知:D是AB上一点,
E是AC上一点,BE、CD相交于点F,∠A=62?,∠ACD=35?,∠ABE=20?.
求:(1)∠BDC的度数;
(2)∠BFD的度数.
A
B
C
D
F
E
解:(1)
∵∠BDC
=∠A+∠ACD
(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠BDC=62?+35?=97?
D
F
E
C
A
B
(2)∵∠BFD=180?-∠BDC -∠ABE
(三角形的三个内角和等于180?)
∴∠BFD=180?-97?-20?
=63?
开阔视野
我们知道,三角形的三个内角的和是180°,那么四边形四个内角的和为多少度?五边形呢?......
填写下表,你找到什么规律?你也可以用几何画板或其他几何软件来探索.
多边形
内角和
三角形
四边形
五边形
…
…
n
边形
180°
360°
540°
180°(
n-2
)
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?
B
A
C
用圆规画最简便。
你能通过折纸的方法得到它吗?
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合。
折痕AD即为三角形的∠A的角平分线。
A
B
C
A
D
做一做
三形的角平分线的定义
以前所学的“角平分线”是一条射线,
B
A
C
“三角形的角平分线”
还是射线
吗?
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的
线段叫三角形的角平分线。
“三角形的角平分线”是一条线段。
D
∠1=∠2
1
2
图5?10
三角形的角平分线的性质
每人在纸张上分别画一个锐角三角形、钝角三角形和直角三角形。
(1)
你能分别画出这三个三角形的三条角平分线吗?
做一做
(2)
在每个三角形中,这三条角平分线之间有怎样的
位置关系?
将你的结果与同伴进行交流.
三角形的三条角平分线交于同一点.
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”
BE=EC
图5?11
B
C
E
A
如图5?1l,
AE是BC边上的中线.
(1)
在纸上画出一个锐角三角形,并画出它的三条中线.
议一议
它们有怎样的位置关系?
与同伴进行交流.
(2)
钝角三角形和直角三角形的三条中线
也有同样的位置关系吗?
三角形的三条中线的性质
三角形的三条中线交于一点.
已知ΔABC(如图),画中线AD和角平分线BE。
A
C
B
1.
AD是ΔABC的角平分线(如图),那么∠BAC=
∠BAD;
2.
AE是ΔABC的中线(如图),那么
BE
=
___BC。
A
D
C
B
A
B
C
E
2
课内训练
1.如图在△ABC中∠ACE=∠BCE,BD=CD,则AD是三角形_____的_____线,CE是三角形_____的______线。
2.如图,在三角形ABC中,BD是角平分线,BE是中线,如果AC=10cm,则AE=____cm,如果∠ABC=60°,则∠ABD=______
3.如图在三角形ABC中,AD平分∠BAC,DE∥AC交AB于E点,若∠BAC=40°,则
∠EDA=______
A
B
C
D
E
4.能把三角形的面积平分的是三角形的______
5.如图AD是△ABC的BC边上的中线,DE是△ADC的AC边上的中线,若△ABC面积等于4,则△ADE的面积等于_________
。
回
顾
思
考
你还记得
“过一点画已知直线的垂线”
吗?
回顾
思考
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
画法
放、
靠、
过、
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
画。
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高
(height)
如图
∵
线段AD是BC边上的高.
图1?12
A
B
C
D
∴
AD⊥BC
∠
ADB=∠ADC=90
注意
!
标明
垂直的记号
和垂足的字母.
锐角三角形的三条高
锐角三角形图
(1)
你能画出这个三角形的
高吗?有几条呢?
画一画
(2)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
O
锐角三角形的三条高是
在三角形的内部还是外部?
锐角三角形的三条高
都在三角形的内部。
A
B
C
D
E
F
直角三角形的三条高
直角三角形图
做一做
将你的结果与同伴进行交流.
A
B
C
(1)
画出直角三角形的三条高,
直角边BC边上的高是
;
AB边
直角边AB边上的高是
;
BC边
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是______
BD
画钝角三角形的三条高
钝角三角形。
画一画
你能画出钝角三角形的三条高吗?
A
B
C
BC边上的高是在三角形的内部还是外部?
外部
D
AB边上的高呢?
E
F
钝角三角形的三条高
议一议
A
B
C
D
F
钝角三角形的
三条高交于一点吗?
钝
角三角形的
三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高所在直线交于一点
O
E
钝角三角形的三条高
议一议
A
B
C
F
钝角三角形的
三条高交于一点吗?
钝
角三角形的
三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高所在直线交于一点
O
E
D
想一想
分别指出图1—13中△ABC
的三条高。
直角边BC边上的
高是
;
AB边
直角边AB边上的
高是
;
CB边
A
B
C
D
E
F
想一想
A
B
C
D
图1—13
斜边AC边上的
高是
;
BD
AB边上的高是
;
CE
BC边上的高是
;
AD
CA边上的高是
;
BF
例1、如图在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小。
A
B
C
D
E
解:
∵
AD是△ABC的高
∴∠ADC=90°
∵
∠ADC+∠C+∠DAC=180°
∴
∠DAC=180°-(∠ADC+∠C)
=180°-90°-40°
=50°
∵AE是△ABC的角平分线且∠BAC=82°
∴∠CAE=
∠BAC=41°
∴∠DAE=∠DAC-∠CAE=50°-41°=9°
例2.如图在△ABC中,AE,AD分别是BC
边上的中线和高线,说明△ABE的面积和△AEC的面积相等.
A
B
C
E
D
问题1:三角形的面积公式是什么?
问题2:根据三角形的面积公式和图中的线段,你能表示△
ABE和△
ACE的面积吗?
问题3:结合中线定义知道哪两条线段相等,这样比较上面的两个三角形的面积表达式可得到结论了吗?
本
课
概
要
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么
a2+b2=c2
即
:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
总统证法
你能只用这两个直角三角形说明a2+b2=c2吗?
一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解:
过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
应用知识之学海无涯
从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形状?
在我们的生活中有没有这样的形状?能举例子吗?
三角形(1)
认识三角形
定义:不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
一.三角形的定义
×
×
×
√
×
×
首
1、顶点:
用一个大写字母表示如A、B、C
2、边:
边AB,边BC,边AC
3、角(内角):
相邻两边
的夹角
∠A,∠B,∠C
4、三角形记作:△ABC
A
B
C
5、对角:
对边:
∠C的对边是BA
BC边的对角是∠A
二.三角形的相关概念
A
B
C
在△ABC中
a
b
c
D
三角形外角的定义:三角形内角的一边与另一边
的反向延长线所组成的角叫做三角形的外角。
B
A
C
1
2
E
6.外角
∠ACD
∠BCE
请画出△ABC的所有外角.
.
.
.
所有外角
3
(
(
2
(
1
(
4
(
5
(
6
例:下图中有几个三角形?并把它们表示出来
指出△ADC的三个内角、三条边
A
B
C
D
(1)∠ADC能写成∠D吗?∠ACD能写成∠C吗?为什么?
(2)有人说CD是△ACD和△BCD的公共的边,对吗?AD是△ACD和△ABD的公共边,对吗?
(3)∠BDC是△BCD的什么角?
提问
例、图中以BC为边的三角形共有______个;它们分别______________________________.
在△ABD中,∠A是_______边的对角,
∠ADB是△_____的内角,又是________________的一个外角.
D
B
E
C
F
A
4
△BCF;
△
BCE;
△
BCD;
△
BCA
△FDC
或△BDC
ABD
BD
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形(不规则三角形)
等腰三角形
三.三角形的分类
只有两条边相等的等腰三角形
等边三角形
斜三角形
说出你所知道的各种三角形的名称
等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
不等边三角形
a
c
b
a
a
a
a
a
b
等腰三角形中,相等的边叫腰,另一边叫底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
底
腰
腰
顶角
底角
底角
等腰三角形和等边三角形为特殊的三角形
1.图中有几个三角形?
用符号表示这些三角形。
A
B
C
D
E
△ABE
△BEC
△DEC
△ABC
△DBC
注:表示三角形时,字母没有先后顺序;
四.练习
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE
4.说出其中ΔBCD的三个角?
∠BCD
、
∠CBD
、∠D
A
B
C
D
E
l、三角形的概念,一个三角形有三个顶点,三条边,三个内角,六个外角,和三角形一个内角相邻的外角有2个,它们是对顶角,若一个顶点只取一个外角,那么只有3个外角。
五.知识巩固
2.三角形的分类:按角分为三类:①锐角三角形,②直角三角形,③钝角三角形。按边分为三类:①三边都不相等的三角形;②等腰三角形。
等边三角形只是等腰三角形中的一种特殊的三角形。
2.掌握了三角形的基本要素及其表示法;
3.学会对三角形进行合理分类,并了解
分类的基本原理;
4、学会用数学知识进行说理.
1、本节通过贴近我们生活的图片出发,体验了三角形知识的产生过程;
六.课堂总结
知识背景
1.
叫做三角形
由不在同一条直线上的三条线段首尾顺次相接所组成的图形
2.
三角形边的性质:
三角形任何两边的和大于第三边
三角形任何两边的差小于第三边
3.
角的分类:
锐角
(小于直角的角)
直角
(等于90°的角)
钝角
(大于直角而小于平角的角)
平角
(等于180°的角)
周角
(等于360°的角)
∠A+∠B+∠C=180°
即三角形三个内角的和等于180°
你能用其他方法得到相同的发现吗?
自主发现
例1
:
在△ABC中,如图,已知∠A=45°,∠B=30°,求∠C的度数。
A
C
B
变式1:在△
ABC中,∠A=45°,∠B=
2∠C,求∠B、
∠C的度数。
变式2:在△
ABC中,∠A=∠B=2∠C,求∠B、
∠C的度数。
三角形可以按内角的大小进行分类:
三角形
锐角三角形
(acute
triangle)
三个内角都是锐角
A
C
B
直角三角形
(right
triangle)
有一个内角是直角
A
C
B
钝角三角形
(obtuse
triangle)
有一个内角是钝角
A
C
B
(1)
在三角形中,最多有几个锐角?几个钝角?几个直角呢?
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
将下面的这些三角形进行分类:
?
请你判断
?
1.
如果
的两内角互余,则
按角分类是
三角形
ABC
ABC
直角
ABC
2.
若∠A=72°,∠B=41°,则
按角分类是
三角形
锐角
ABC
3.
若∠A+∠B=∠C,则
按角分类是
三角形
直角
4.
对于三角形的内角,下列判断不正确的是(
)
A.至少有两个锐角
B.最多有一个直角
C.必有一个角大于60°
D.至少有一个角不小于60°
C
与三角形的内角直接相关的
一个概念是三角形的外角。
A
B
C
D
如图,∠ACD由
一
条边BC的延长线和另一
条相邻的边AC组成的角,
叫做该三角形的
外角(exterior
angle)
ABC
(2)
A
B
C
D
如图,∠ACD是
一外角.
ABC
(1)你能通过延长各边,将
的所有的外角表示出来吗?
一个三角形有多少个外角?
ABC
(2)外角∠ACD与两个和它不相
邻的内角有什么关系?
请与
你的同伴交流一下.
三角形的一个外角等于和它不相邻的两个内角的和
梳理知识
三角形的一个外角等于和
它不相邻的两个内角的和
A
B
C
D
ABC
在
中,
∠ACD是
一外角.
ABC
你能结合图形用数学式子来表示吗?
∠ACD=∠A+∠B
你能用学过的知识加以解释吗?
∵∠A+∠B+∠ACB=180°
又∵∠ACB+∠ACD=180°
∴
∠ACD=∠A+∠B
?
?
巩固练习
A
B
C
D
(1)若∠A=74°,∠B=42°,
则∠ACD=
.
(2)若∠ACD=114
°36′,
∠A=65°,则∠B=
.
116°
49°36′
ABC
在
中,
如图,
∠ACD是
外角.
ABC
1.
2.在下面这幅埃及金字塔图中,三角形有两个内角相等,相等内角的一个外角等于135°,求图中三角形的各内角的度数。
135°
A
B
C
D
解:
∵∠ACB+∠ACD=180°
∠ACD=135°
∴∠ACB=180°-135°=45°
∴∠B=∠ACB=45°
又∵∠A+∠B+∠ACB=180°
∴∠A=180°-(∠A+∠B)=90°
①三角形的一个外角等于其它不相邻的两个内角和;
②三角形的一个外角,大于任何一个和它不相邻的内角.
A
B
C
D
例2:一把椅子的结构如图,
∠1=∠2当椅面水平时,
∠3=100°,此时∠1的度数是多少?
1
2
3
1
2
3
解:
∵
∠3是△ABC的一个外角
∴∠3=
∠1+∠2
(三角形的一个外角等于和它不相邻的两个内角的和)
∵
∠1=∠2
∴
∠3=
2∠1
∴
∠1=
∠2
=
1/2∠3=1/2×100
°
=50
°
A
B
C
课堂达标
1.
三角形按角分类,可以分为
三角形,
三角形,
三角形
锐角
直角
钝角
ABC
2.在
中,
(1)若∠A=54°,∠B=27°,则∠C=
.
99°
(2)若∠B=∠C=30°,则∠A=
,
为
三角形
ABC
120°
钝角
(3)若∠A:∠B:∠C=1:2:3,则∠A=
,∠B=
,∠C
=
.
30°
60°
90°
ABC
3.
如图,在Rt
中,∠ACB=90°,CD⊥AB,垂足为D,则可
以推得∠ACD=∠B.试把下面的推理过程填写完整:
A
C
D
B
解:
∵∠ACB=90°(
已知
)
∴∠ACD+∠BCD=
.
∵CD⊥AB
(
)
∴∠CDB=∠ADC=90°
∴∠B+∠BCD
=∠ADC=90°(
)
∴∠ACD=∠B
已知
三角形的一个外角等于和它不相邻的两个内角的和
90°
例3.已知如图:∠BAF、∠CBD、
∠ACE是△ABC的三个外角。
说明:∠BAF+∠CBD+∠ACE=3600
E
A
F
B
D
C
1
2
3
证明:如图,
A
B
D
C
1
2
3
F
∠BAF=∠2+∠3,
∠CBD=∠1+∠3,
∠ACE=∠1+∠2
(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠BAF+∠CBD+∠ACE
=(∠2+∠3+∠1+∠3+∠1+∠2)
=2(∠1+∠2+∠3)
例4 已知:D是AB上一点,
E是AC上一点,BE、CD相交于点F,∠A=62?,∠ACD=35?,∠ABE=20?.
求:(1)∠BDC的度数;
(2)∠BFD的度数.
A
B
C
D
F
E
解:(1)
∵∠BDC
=∠A+∠ACD
(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠BDC=62?+35?=97?
D
F
E
C
A
B
(2)∵∠BFD=180?-∠BDC -∠ABE
(三角形的三个内角和等于180?)
∴∠BFD=180?-97?-20?
=63?
开阔视野
我们知道,三角形的三个内角的和是180°,那么四边形四个内角的和为多少度?五边形呢?......
填写下表,你找到什么规律?你也可以用几何画板或其他几何软件来探索.
多边形
内角和
三角形
四边形
五边形
…
…
n
边形
180°
360°
540°
180°(
n-2
)
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?
B
A
C
用圆规画最简便。
你能通过折纸的方法得到它吗?
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合。
折痕AD即为三角形的∠A的角平分线。
A
B
C
A
D
做一做
三形的角平分线的定义
以前所学的“角平分线”是一条射线,
B
A
C
“三角形的角平分线”
还是射线
吗?
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的
线段叫三角形的角平分线。
“三角形的角平分线”是一条线段。
D
∠1=∠2
1
2
图5?10
三角形的角平分线的性质
每人在纸张上分别画一个锐角三角形、钝角三角形和直角三角形。
(1)
你能分别画出这三个三角形的三条角平分线吗?
做一做
(2)
在每个三角形中,这三条角平分线之间有怎样的
位置关系?
将你的结果与同伴进行交流.
三角形的三条角平分线交于同一点.
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线(median).
三角形的“中线”
BE=EC
图5?11
B
C
E
A
如图5?1l,
AE是BC边上的中线.
(1)
在纸上画出一个锐角三角形,并画出它的三条中线.
议一议
它们有怎样的位置关系?
与同伴进行交流.
(2)
钝角三角形和直角三角形的三条中线
也有同样的位置关系吗?
三角形的三条中线的性质
三角形的三条中线交于一点.
已知ΔABC(如图),画中线AD和角平分线BE。
A
C
B
1.
AD是ΔABC的角平分线(如图),那么∠BAC=
∠BAD;
2.
AE是ΔABC的中线(如图),那么
BE
=
___BC。
A
D
C
B
A
B
C
E
2
课内训练
1.如图在△ABC中∠ACE=∠BCE,BD=CD,则AD是三角形_____的_____线,CE是三角形_____的______线。
2.如图,在三角形ABC中,BD是角平分线,BE是中线,如果AC=10cm,则AE=____cm,如果∠ABC=60°,则∠ABD=______
3.如图在三角形ABC中,AD平分∠BAC,DE∥AC交AB于E点,若∠BAC=40°,则
∠EDA=______
A
B
C
D
E
4.能把三角形的面积平分的是三角形的______
5.如图AD是△ABC的BC边上的中线,DE是△ADC的AC边上的中线,若△ABC面积等于4,则△ADE的面积等于_________
。
回
顾
思
考
你还记得
“过一点画已知直线的垂线”
吗?
回顾
思考
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
画法
放、
靠、
过、
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
画。
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高
(height)
如图
∵
线段AD是BC边上的高.
图1?12
A
B
C
D
∴
AD⊥BC
∠
ADB=∠ADC=90
注意
!
标明
垂直的记号
和垂足的字母.
锐角三角形的三条高
锐角三角形图
(1)
你能画出这个三角形的
高吗?有几条呢?
画一画
(2)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
O
锐角三角形的三条高是
在三角形的内部还是外部?
锐角三角形的三条高
都在三角形的内部。
A
B
C
D
E
F
直角三角形的三条高
直角三角形图
做一做
将你的结果与同伴进行交流.
A
B
C
(1)
画出直角三角形的三条高,
直角边BC边上的高是
;
AB边
直角边AB边上的高是
;
BC边
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是______
BD
画钝角三角形的三条高
钝角三角形。
画一画
你能画出钝角三角形的三条高吗?
A
B
C
BC边上的高是在三角形的内部还是外部?
外部
D
AB边上的高呢?
E
F
钝角三角形的三条高
议一议
A
B
C
D
F
钝角三角形的
三条高交于一点吗?
钝
角三角形的
三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高所在直线交于一点
O
E
钝角三角形的三条高
议一议
A
B
C
F
钝角三角形的
三条高交于一点吗?
钝
角三角形的
三条高不相交于一点
它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高所在直线交于一点
O
E
D
想一想
分别指出图1—13中△ABC
的三条高。
直角边BC边上的
高是
;
AB边
直角边AB边上的
高是
;
CB边
A
B
C
D
E
F
想一想
A
B
C
D
图1—13
斜边AC边上的
高是
;
BD
AB边上的高是
;
CE
BC边上的高是
;
AD
CA边上的高是
;
BF
例1、如图在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=82°,∠C=40°,求∠DAE的大小。
A
B
C
D
E
解:
∵
AD是△ABC的高
∴∠ADC=90°
∵
∠ADC+∠C+∠DAC=180°
∴
∠DAC=180°-(∠ADC+∠C)
=180°-90°-40°
=50°
∵AE是△ABC的角平分线且∠BAC=82°
∴∠CAE=
∠BAC=41°
∴∠DAE=∠DAC-∠CAE=50°-41°=9°
例2.如图在△ABC中,AE,AD分别是BC
边上的中线和高线,说明△ABE的面积和△AEC的面积相等.
A
B
C
E
D
问题1:三角形的面积公式是什么?
问题2:根据三角形的面积公式和图中的线段,你能表示△
ABE和△
ACE的面积吗?
问题3:结合中线定义知道哪两条线段相等,这样比较上面的两个三角形的面积表达式可得到结论了吗?
本
课
概
要
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
勾股定理(gou-gu
theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么
a2+b2=c2
即
:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
勾
股
勾
股
弦
我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
辉煌发现
a
b
c
b
a
c
A
B
C
D
E
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
总统证法
你能只用这两个直角三角形说明a2+b2=c2吗?
一个长方形零件(如图),根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解:
过A作铅垂线,过B作水平线,两线交于点C,则
∠ACB=90°,
AC=90-40=50(mm)
BC=160-40=120(mm)
由勾股定理有:
AB2=AC2+BC2=502+1202
=16900(mm2)
∵AB>0,
∴AB=130(mm)
答:两孔中心A,B的距离为130mm.
应用知识之学海无涯
同课章节目录
