人教版八年级上册11.2 与三角形有关的角同步练习卷(Word版含答案)
文档属性
| 名称 | 人教版八年级上册11.2 与三角形有关的角同步练习卷(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 404.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览


文档简介
11.2
与三角形有关的角练习卷普通用卷
总分:100分
一
单选题
(共12题
,总分值36分
)
1.
在给定的下列条件中,不能判定三角形是直角三角形的是(
)
(3
分)
A.
∠A∶∠B∶∠C=1∶2∶3
B.
∠A+∠B=∠C
C.
∠A=∠B=∠C
D.
∠A=2∠B=3∠C
2.
若一个三角形的三个外角的度数之比是5∶4∶5,则这个三角形是(
)
(3
分)
A.
等腰三角形,但不是等腰直角三角形或等边三角形
B.
等边三角形
C.
等腰三角形
D.
等腰直角三角形
3.
如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为(
)(3
分)
A.
17°
B.
62°
C.
63°
D.
73°
4.
如图,已知点D,E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为(
)(3
分)
A.
100°
B.
90°
C.
80°
D.
70°
5.
将一副三角板桉图中方式叠放,则角
的度数是(
)(3
分)
A.
30?
B.
45?
C.
60?
D.
75?
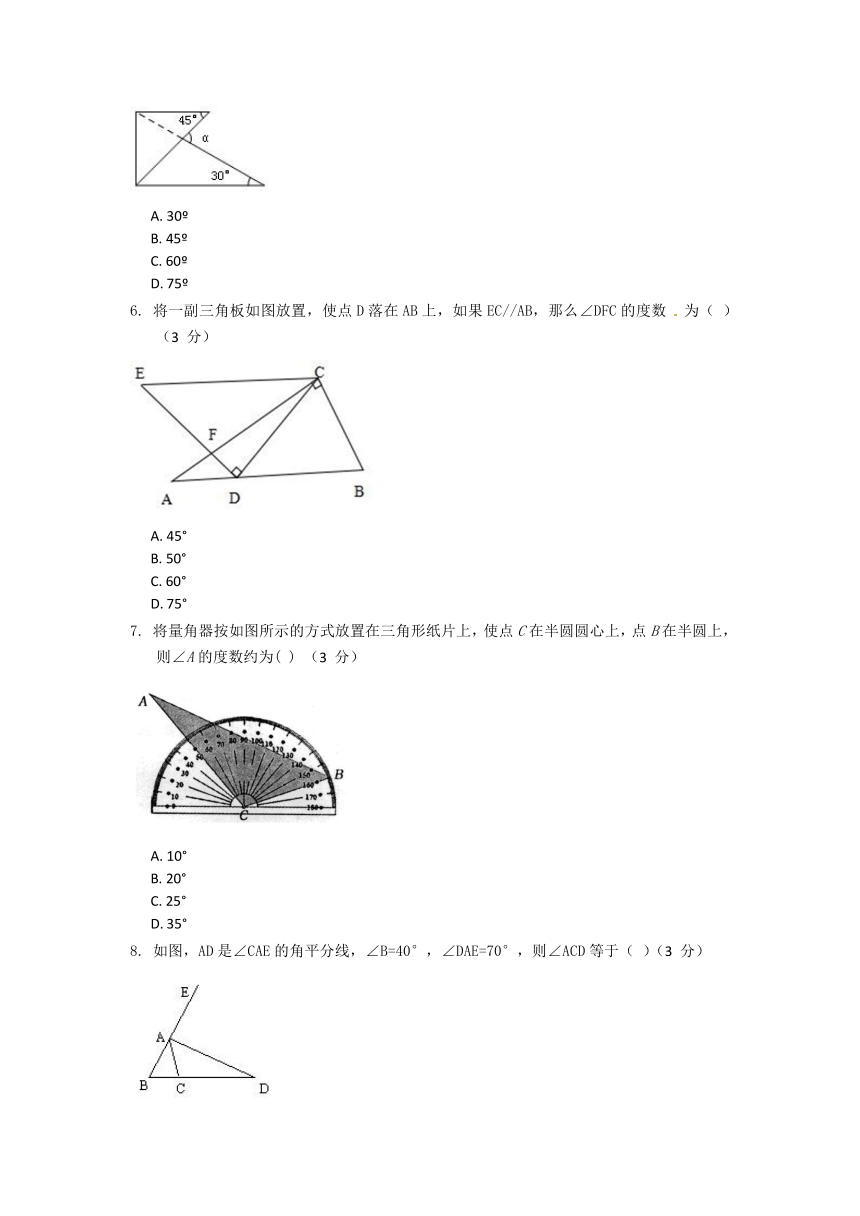
6.
将一副三角板如图放置,使点D落在AB上,如果EC//AB,那么∠DFC的度数
为(
)(3
分)
A.
45°
B.
50°
C.
60°
D.
75°
7.
将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,则∠A的度数约为(
)
(3
分)
A.
10°
B.
20°
C.
25°
D.
35°
8.
如图,AD是∠CAE的角平分线,∠B=40°,∠DAE=70°,则∠ACD等于(
)(3
分)
A.
150°
B.
80°
C.
110°
D.
100°
9.
如图所示,在△ABC中,∠B=∠C,∠BAD=40°,若∠1=∠2,则∠EDC的度数为(
)(3
分)
A.
40°
B.
30°
C.
20°
D.
10°
10.
如图,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处。下面结论错误的是(
)(3
分)
A.
AB=BE
B.
AD=DC
C.
AD=DE
D.
AD=EC
11.
如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=(
)(3
分)
A.
225°
B.
235°
C.
270°
D.
与虚线的位置有关
12.
如图,在四边形ABCD中,∠B=120°,∠D=50°,将∠C向内折出一个△PRC′,恰好使C′P∥AB,C′R∥AD,则∠C的度数是(
)(3
分)
A.
80°
B.
85°
C.
95°
D.
110°
二
填空题
(共6题
,总分值18分
)
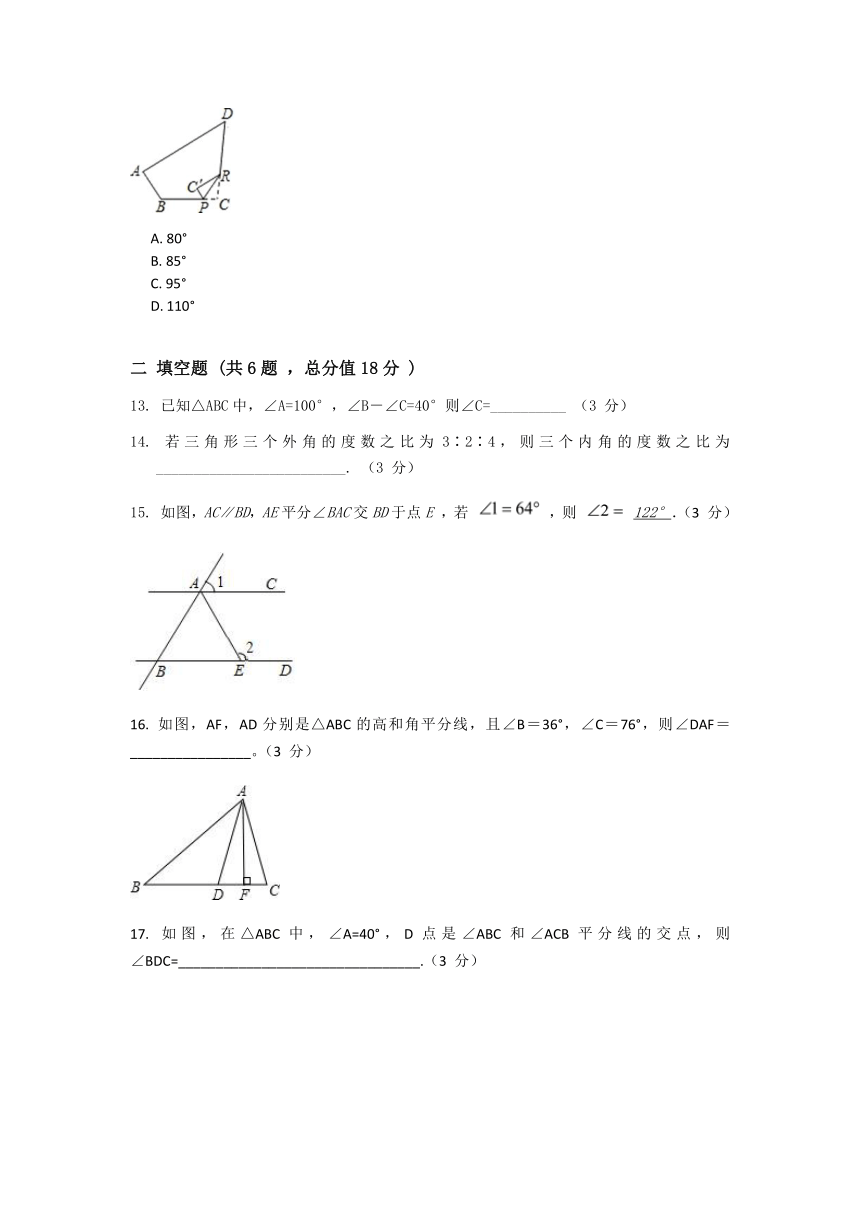
13.
已知△ABC中,∠A=100°,∠B-∠C=40°则∠C=__________
(3
分)
14.
若三角形三个外角的度数之比为3∶2∶4,则三个内角的度数之比为_________________________.
(3
分)
15.
如图,AC∥BD,AE平分∠BAC交BD于点E
,若
,则
122°.(3
分)
16.
如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAF=________________。(3
分)
17.
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB平分线的交点,则∠BDC=________________________________.(3
分)
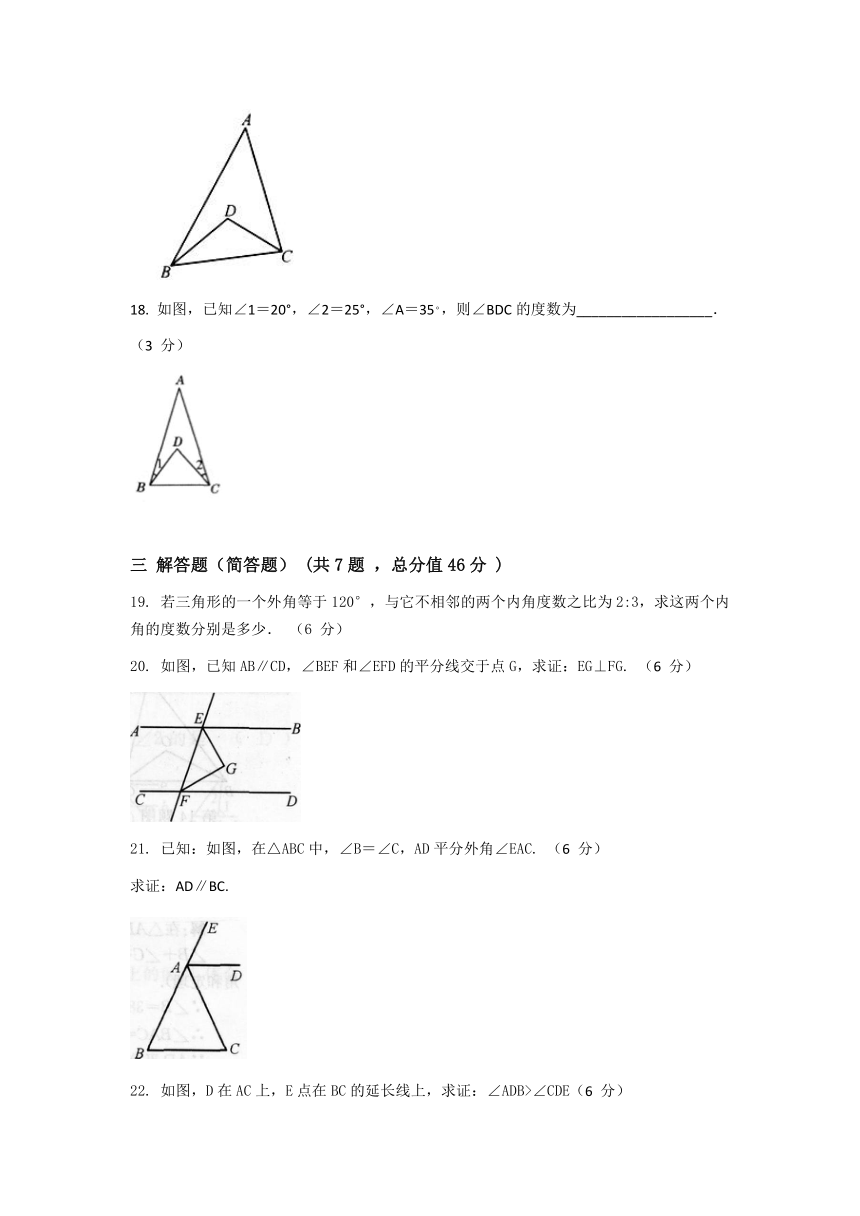
18.
如图,已知∠1=20°,∠2=25°,∠A=35。,则∠BDC的度数为__________________.
(3
分)
三
解答题(简答题)
(共7题
,总分值46分
)
19.
若三角形的一个外角等于120°,与它不相邻的两个内角度数之比为2:3,求这两个内角的度数分别是多少.
(6
分)
20.
如图,已知AB∥CD,∠BEF和∠EFD的平分线交于点G,求证:EG⊥FG.
(6
分)
21.
已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
(6
分)
求证:AD∥BC.
22.
如图,D在AC上,E点在BC的延长线上,求证:∠ADB>∠CDE(6
分)
23.
在△ABC中,
,BD是
平分线,求
及
的度数。(6
分)
24.
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数。(8
分)
25.
如图,△ABC中,延长BC到D,∠ABC和∠ACD的平分线相交于点P.
(1)若∠A=50°,则∠P=________________________________________;
(2)若∠A=60°,则∠P=________________________________________;
(3)若∠A=70°,则∠P=________________________________________;
(4)根据上述规律,若∠A=100°,则∠P=__________________________________,
(5)请你用数学表达式归纳出∠P与∠A的关系:___________________________________;
(6)请说明你的结论正确的理由.
(8
分)
一
单选题
(共12题
,总分值36分
)
1.
答案:C
解析过程:利用比例设方程,A、B、D中都有直角,C选项中三角相等则每一角为60°,则选C。
2.
答案:A
解析过程:
3.
答案:D
解析过程:思路分析:
考点解剖:本题考查平行线的性质以及三角形内角与外角的性质,难度较小.
解题思路:首先根据两直线平行,内错角相等可得∠ABC=∠C=28°,再根据三角形内角与外角的性质可得∠AEC=∠A+∠ABC.
解答过程:
解:∵
,∴
,又∵
,
∴
,故选D.
规律总结:
平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;反过来可得平行线的判定,即:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
4.
答案:C
解析过程:先由
,得
(两直线平行,同位角相等),再根据三角形内角和定理,可得
,故选C.
5.
答案:D
解析过程:思路分析:
考点解剖:本题考查了三角形的内角和定理及三角形的一个外角与不相邻的两个内角之间的关系,解答此题时,注意将所要求的角转化成可求解的角来表示.
解题思路:1.先求出∠1的度数,再利用∠
=∠1+30?求出∠
;2.先根据三角板各内角的度数求出∠3的度数,再利用对顶角相等求出∠
.
解答过程:
解:由三角板知:∠2=45?,∠4=60?.方法一:∠1=90?-∠2=90?-45?=45?,∠
=∠1+30?=45?+30?=75?.方法二:∠3=180?-∠2-∠4=180?-45?-60?=75?.根据对顶角相等可知∠
=∠3=75?.
规律总结:
能发现并将所要求解的角通过转化思想转化为已知角的和(或差、或倍、几分这几)等关系去表示.
6.
答案:D
解析过程:∵EC//AB,∴∠CED=∠ADE=45°,∠CAD=∠ACE=30°,
∴∠DFC=∠ADE+CAD=75°.故选D.
7.
答案:C
解析过程:思路分析:
考点解剖:以三角形为背景的图形求角时,要充分利用三角形内角和及三角形内外角之间的关系把已知角与未知角联系起来.
解题思路:根据CD=BD容易得出∠CDB=∠CBD,根据图上示数,容易求出∠B的度数,再利用三角形内角和180°求出∠A度数.
解答过程:
解:如图,设AB与半圆交于点D,连结CD,
由量角器上的度数可得∠BCD=160°-70°=90°,∠ACD=70°-50°=20°,
在△BCD中,∵CB=CD,
∴∠BDC=∠B=
(180°-∠BCD)=
(180°-90°)=45°,
再由三角形内外角的关系可得∠A=∠BDC-∠ACD=45°-20°=25°,故选C.
规律总结:将抽象的几何模型实物操作,问题转化为数学知识是解决此问题的关键.
8.
答案:B
解析过程:
9.
答案:C
解析过程:由图可知∠ADC=∠B+∠BAD,∠ADC=∠1+∠EDC=∠2+∠EDC,得出∠B+∠BAD=∠2+∠EDC。由∠2=∠EDC+∠C,得∠B+∠BAD=∠EDC+∠EDC+∠C。而∠B=∠C,所以∠BAD=2∠EDC,求得∠EDC=20°。
10.
答案:B
解析过程:由翻折、轴对称性质得:AB=BE,AD=DE,由等腰直角三角形的性质可知DE=EC,即AD=DE=EC,所以只有B选项是错的。
11.
答案:C
解析过程:思路分析:
考点解剖:本题考查了三角形外角和性质(或多边形的内角和).掌握三角形外角和是几个外角的和是关键.
解题思路:由于三角形的外角和是三个外角的和,即每个顶点处的一个外角的和,故∠1、∠2和90分别是三角形三个顶点出的外角,所以由三角形的外角和是360°,可求∠1+∠2的度数.
解答过程:
解∠1+∠2+90°=360°,∴∠1+∠2=270°.故选C.
规律总结:
任何多边形的内角和都等于360°.
12.
答案:C
解析过程:根据折叠前后图形全等和平行线,先求出∠CPR和∠CRP,再根据三角形内角和定理即可求出∠C.
解:因为折叠前后两个图形全等,故∠CPR=
∠B=
×120°=60°,
∠CRP=
∠D=
×50°=25°;
∴∠C=180°﹣25°﹣60°=95°;
∴∠C=95°;
故选C.
点评:本题主要考查了三角形的内角和外角之间的关系平行线的性质和翻折变换.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
二
填空题
(共6题
,总分值18分
)
13.
答案:20°
解析过程:
14.
答案:3:5:1
解析过程:分析:已知三角形三个外角的度数之比,可以设一份为k°,根据三角形的外角和等于360°列方程求三个内角的度数,确定三角形内角的度数,然后求出度数之比.
解:设一份为k°,则三个外角的度数分别为3k°,2k°,4k°,
根据三角形外角和定理,可知3k°+2k°+4k°=360°,得k°=40°,
三个外角分别为120°,80°和160°,
根据三角形外角与它相邻的内角互补,与之对应的三个内角的度数分别是60°,100°和20°,
即三个内角的度数的比为3:5:1.
15.
答案:122°
解析过程:思路分析:
考点解剖:考查了平行线的性质,角平分线的定义,邻补角的定义以及三角形外角的性质.
解题思路:由AC∥BD,根据两直线平行,同位角相等,即可求得∠B的度数;由邻补角的定义,求得∠BAC的度数;又由AE平分∠BAC交BD于点E,即可求得∠BAE的度数,根据三角形外角的性质即可求得∠2的度数.
解答过程:
解:解法一:∵AC∥BD,∴∠B=∠1=64°,
∴∠BAC=180°﹣∠1=180°﹣64°=116°,
∵AE平分∠BAC交BD于点E,
∴∠BAE=
∠BAC=58°,
∴∠2=∠BAE+∠B=64°+58°=122°.
解法二:∵∠1+∠BAC=180°,
∠1=64°,
∴∠BAC=116°.
∵AE平分∠BAC.
∴∠CAE=58°.
∵AC∥BD
∴∠CAE+∠2=180°.
∴∠2=180°-58°=122°.
故答案为:∠2=180°-58°=122°.
规律总结:在平行的条件下计算角度,一般情况下要用到平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
16.
答案:20°
解析过程:思路分析:
1)题意分析:本题考查三角形内角和定理;三角形角平分线、高线的定义。
2)解题思路:根据三角形内角和定理先求出∠BAC的度数,再根据角平分线的定义求出∠CAD的度数,根据高的定义求出∠CAF的度数,从而求出∠DAF的度数。
解答过程:
∵∠B=36°,∠C=76°,
∴∠BAC=180°-∠B-∠C=180°-76°-36°=68°,
又∵AD是∠BAC的平分线,
∴∠CAD=68°×
=34°,
在Rt△AFC中,∠FAC=90°-∠C=90°-76°=14°
于是∠DAF=34°-14°=20°。
解题后的思考:解答本题的关键是熟练掌握角平分线、高线及三角形内角和定理。
17.
答案:110°
解析过程:
18.
答案:80°
解析过程:本题可利用整体思想求解.
在△BDC中,
.
∵
,
,
∴
.
在△ABC中,
,
∴
,
∴
.
三
解答题(简答题)
(共7题
,总分值46分
)
19.
答案:两个内角的度数分别是48°,72°.
解析过程:设这两个内角的度数是2x°,3x°,则
.所以
,即
,
.所以这两个内角的度数分别是48°,72°.
20.
答案:证明:∵AB∥CD,
∴∠BEF+∠EFD=180°.
∵∠BEF和∠EFD的平分线交于点G,
∴
,
.
∴
.
∴∠G=90°.
∴EG⊥FG.
解析过程:
21.
答案:证明:∵∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角和),∠B=∠C(已知),
∴
(等式的性质).
∵AD平分∠EAC(已知),
∴∠
(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥BC(内错角相等,两直线平行).
解析过程::要证明AD∥BC,只需证明“同位角相等”或“内错角相等”或“同旁内角互补”.
22.
答案:见解析
解析过程:证明:∵∠DCB是△DCE的一个外角(外角定义)
∴∠DCB>∠CDE(三角形的一个外角大于任何一个和它不相邻的内角)
∵∠ADB是△BCD的一个外角(外角定义)
∴∠ADB>∠DCB(三角形的一个外角大于任何一个和它不相邻的内角)
∴∠ADB>∠CDE(不等式的性质).
23.
答案:
,
解析过程:∵BD是
的平分线,∴
。
∵
,∴
。
∴
。设
,
由
,得
,解得
。∴
,
24.
答案:24°
解析过程:∵∠1=∠2,∠3=∠4,∠3=∠1+∠2,
∴2∠2=∠4,
∵∠2+∠4+∠BAC=180°,
∴∠2+2∠2+63°=180°,
∴3∠2+63°=180°
∴∠1=∠2=39°,
∠DAC=∠BAC-∠1=63°-39°=24°。
25.
答案:(1)25° (2)30° (3)35° (4)50° (5)
(6)∵∠ACD=∠ACP+
∠PCD=∠A+
∠ABC,∠ACP=∠PCD,∠ABP=∠PBC,∴2∠PCD=∠A+
2∠PBC.∵∠PCD=∠P+∠PBC,∴2(∠P+∠PBC)=∠A+2∠PBC.∴
.
与三角形有关的角练习卷普通用卷
总分:100分
一
单选题
(共12题
,总分值36分
)
1.
在给定的下列条件中,不能判定三角形是直角三角形的是(
)
(3
分)
A.
∠A∶∠B∶∠C=1∶2∶3
B.
∠A+∠B=∠C
C.
∠A=∠B=∠C
D.
∠A=2∠B=3∠C
2.
若一个三角形的三个外角的度数之比是5∶4∶5,则这个三角形是(
)
(3
分)
A.
等腰三角形,但不是等腰直角三角形或等边三角形
B.
等边三角形
C.
等腰三角形
D.
等腰直角三角形
3.
如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为(
)(3
分)
A.
17°
B.
62°
C.
63°
D.
73°
4.
如图,已知点D,E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为(
)(3
分)
A.
100°
B.
90°
C.
80°
D.
70°
5.
将一副三角板桉图中方式叠放,则角
的度数是(
)(3
分)
A.
30?
B.
45?
C.
60?
D.
75?
6.
将一副三角板如图放置,使点D落在AB上,如果EC//AB,那么∠DFC的度数
为(
)(3
分)
A.
45°
B.
50°
C.
60°
D.
75°
7.
将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,则∠A的度数约为(
)
(3
分)
A.
10°
B.
20°
C.
25°
D.
35°
8.
如图,AD是∠CAE的角平分线,∠B=40°,∠DAE=70°,则∠ACD等于(
)(3
分)
A.
150°
B.
80°
C.
110°
D.
100°
9.
如图所示,在△ABC中,∠B=∠C,∠BAD=40°,若∠1=∠2,则∠EDC的度数为(
)(3
分)
A.
40°
B.
30°
C.
20°
D.
10°
10.
如图,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处。下面结论错误的是(
)(3
分)
A.
AB=BE
B.
AD=DC
C.
AD=DE
D.
AD=EC
11.
如图,将等腰直角三角形沿虚线裁去顶角后,∠1+∠2=(
)(3
分)
A.
225°
B.
235°
C.
270°
D.
与虚线的位置有关
12.
如图,在四边形ABCD中,∠B=120°,∠D=50°,将∠C向内折出一个△PRC′,恰好使C′P∥AB,C′R∥AD,则∠C的度数是(
)(3
分)
A.
80°
B.
85°
C.
95°
D.
110°
二
填空题
(共6题
,总分值18分
)
13.
已知△ABC中,∠A=100°,∠B-∠C=40°则∠C=__________
(3
分)
14.
若三角形三个外角的度数之比为3∶2∶4,则三个内角的度数之比为_________________________.
(3
分)
15.
如图,AC∥BD,AE平分∠BAC交BD于点E
,若
,则
122°.(3
分)
16.
如图,AF,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAF=________________。(3
分)
17.
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB平分线的交点,则∠BDC=________________________________.(3
分)
18.
如图,已知∠1=20°,∠2=25°,∠A=35。,则∠BDC的度数为__________________.
(3
分)
三
解答题(简答题)
(共7题
,总分值46分
)
19.
若三角形的一个外角等于120°,与它不相邻的两个内角度数之比为2:3,求这两个内角的度数分别是多少.
(6
分)
20.
如图,已知AB∥CD,∠BEF和∠EFD的平分线交于点G,求证:EG⊥FG.
(6
分)
21.
已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
(6
分)
求证:AD∥BC.
22.
如图,D在AC上,E点在BC的延长线上,求证:∠ADB>∠CDE(6
分)
23.
在△ABC中,
,BD是
平分线,求
及
的度数。(6
分)
24.
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数。(8
分)
25.
如图,△ABC中,延长BC到D,∠ABC和∠ACD的平分线相交于点P.
(1)若∠A=50°,则∠P=________________________________________;
(2)若∠A=60°,则∠P=________________________________________;
(3)若∠A=70°,则∠P=________________________________________;
(4)根据上述规律,若∠A=100°,则∠P=__________________________________,
(5)请你用数学表达式归纳出∠P与∠A的关系:___________________________________;
(6)请说明你的结论正确的理由.
(8
分)
一
单选题
(共12题
,总分值36分
)
1.
答案:C
解析过程:利用比例设方程,A、B、D中都有直角,C选项中三角相等则每一角为60°,则选C。
2.
答案:A
解析过程:
3.
答案:D
解析过程:思路分析:
考点解剖:本题考查平行线的性质以及三角形内角与外角的性质,难度较小.
解题思路:首先根据两直线平行,内错角相等可得∠ABC=∠C=28°,再根据三角形内角与外角的性质可得∠AEC=∠A+∠ABC.
解答过程:
解:∵
,∴
,又∵
,
∴
,故选D.
规律总结:
平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;反过来可得平行线的判定,即:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
4.
答案:C
解析过程:先由
,得
(两直线平行,同位角相等),再根据三角形内角和定理,可得
,故选C.
5.
答案:D
解析过程:思路分析:
考点解剖:本题考查了三角形的内角和定理及三角形的一个外角与不相邻的两个内角之间的关系,解答此题时,注意将所要求的角转化成可求解的角来表示.
解题思路:1.先求出∠1的度数,再利用∠
=∠1+30?求出∠
;2.先根据三角板各内角的度数求出∠3的度数,再利用对顶角相等求出∠
.
解答过程:
解:由三角板知:∠2=45?,∠4=60?.方法一:∠1=90?-∠2=90?-45?=45?,∠
=∠1+30?=45?+30?=75?.方法二:∠3=180?-∠2-∠4=180?-45?-60?=75?.根据对顶角相等可知∠
=∠3=75?.
规律总结:
能发现并将所要求解的角通过转化思想转化为已知角的和(或差、或倍、几分这几)等关系去表示.
6.
答案:D
解析过程:∵EC//AB,∴∠CED=∠ADE=45°,∠CAD=∠ACE=30°,
∴∠DFC=∠ADE+CAD=75°.故选D.
7.
答案:C
解析过程:思路分析:
考点解剖:以三角形为背景的图形求角时,要充分利用三角形内角和及三角形内外角之间的关系把已知角与未知角联系起来.
解题思路:根据CD=BD容易得出∠CDB=∠CBD,根据图上示数,容易求出∠B的度数,再利用三角形内角和180°求出∠A度数.
解答过程:
解:如图,设AB与半圆交于点D,连结CD,
由量角器上的度数可得∠BCD=160°-70°=90°,∠ACD=70°-50°=20°,
在△BCD中,∵CB=CD,
∴∠BDC=∠B=
(180°-∠BCD)=
(180°-90°)=45°,
再由三角形内外角的关系可得∠A=∠BDC-∠ACD=45°-20°=25°,故选C.
规律总结:将抽象的几何模型实物操作,问题转化为数学知识是解决此问题的关键.
8.
答案:B
解析过程:
9.
答案:C
解析过程:由图可知∠ADC=∠B+∠BAD,∠ADC=∠1+∠EDC=∠2+∠EDC,得出∠B+∠BAD=∠2+∠EDC。由∠2=∠EDC+∠C,得∠B+∠BAD=∠EDC+∠EDC+∠C。而∠B=∠C,所以∠BAD=2∠EDC,求得∠EDC=20°。
10.
答案:B
解析过程:由翻折、轴对称性质得:AB=BE,AD=DE,由等腰直角三角形的性质可知DE=EC,即AD=DE=EC,所以只有B选项是错的。
11.
答案:C
解析过程:思路分析:
考点解剖:本题考查了三角形外角和性质(或多边形的内角和).掌握三角形外角和是几个外角的和是关键.
解题思路:由于三角形的外角和是三个外角的和,即每个顶点处的一个外角的和,故∠1、∠2和90分别是三角形三个顶点出的外角,所以由三角形的外角和是360°,可求∠1+∠2的度数.
解答过程:
解∠1+∠2+90°=360°,∴∠1+∠2=270°.故选C.
规律总结:
任何多边形的内角和都等于360°.
12.
答案:C
解析过程:根据折叠前后图形全等和平行线,先求出∠CPR和∠CRP,再根据三角形内角和定理即可求出∠C.
解:因为折叠前后两个图形全等,故∠CPR=
∠B=
×120°=60°,
∠CRP=
∠D=
×50°=25°;
∴∠C=180°﹣25°﹣60°=95°;
∴∠C=95°;
故选C.
点评:本题主要考查了三角形的内角和外角之间的关系平行线的性质和翻折变换.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
二
填空题
(共6题
,总分值18分
)
13.
答案:20°
解析过程:
14.
答案:3:5:1
解析过程:分析:已知三角形三个外角的度数之比,可以设一份为k°,根据三角形的外角和等于360°列方程求三个内角的度数,确定三角形内角的度数,然后求出度数之比.
解:设一份为k°,则三个外角的度数分别为3k°,2k°,4k°,
根据三角形外角和定理,可知3k°+2k°+4k°=360°,得k°=40°,
三个外角分别为120°,80°和160°,
根据三角形外角与它相邻的内角互补,与之对应的三个内角的度数分别是60°,100°和20°,
即三个内角的度数的比为3:5:1.
15.
答案:122°
解析过程:思路分析:
考点解剖:考查了平行线的性质,角平分线的定义,邻补角的定义以及三角形外角的性质.
解题思路:由AC∥BD,根据两直线平行,同位角相等,即可求得∠B的度数;由邻补角的定义,求得∠BAC的度数;又由AE平分∠BAC交BD于点E,即可求得∠BAE的度数,根据三角形外角的性质即可求得∠2的度数.
解答过程:
解:解法一:∵AC∥BD,∴∠B=∠1=64°,
∴∠BAC=180°﹣∠1=180°﹣64°=116°,
∵AE平分∠BAC交BD于点E,
∴∠BAE=
∠BAC=58°,
∴∠2=∠BAE+∠B=64°+58°=122°.
解法二:∵∠1+∠BAC=180°,
∠1=64°,
∴∠BAC=116°.
∵AE平分∠BAC.
∴∠CAE=58°.
∵AC∥BD
∴∠CAE+∠2=180°.
∴∠2=180°-58°=122°.
故答案为:∠2=180°-58°=122°.
规律总结:在平行的条件下计算角度,一般情况下要用到平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
16.
答案:20°
解析过程:思路分析:
1)题意分析:本题考查三角形内角和定理;三角形角平分线、高线的定义。
2)解题思路:根据三角形内角和定理先求出∠BAC的度数,再根据角平分线的定义求出∠CAD的度数,根据高的定义求出∠CAF的度数,从而求出∠DAF的度数。
解答过程:
∵∠B=36°,∠C=76°,
∴∠BAC=180°-∠B-∠C=180°-76°-36°=68°,
又∵AD是∠BAC的平分线,
∴∠CAD=68°×
=34°,
在Rt△AFC中,∠FAC=90°-∠C=90°-76°=14°
于是∠DAF=34°-14°=20°。
解题后的思考:解答本题的关键是熟练掌握角平分线、高线及三角形内角和定理。
17.
答案:110°
解析过程:
18.
答案:80°
解析过程:本题可利用整体思想求解.
在△BDC中,
.
∵
,
,
∴
.
在△ABC中,
,
∴
,
∴
.
三
解答题(简答题)
(共7题
,总分值46分
)
19.
答案:两个内角的度数分别是48°,72°.
解析过程:设这两个内角的度数是2x°,3x°,则
.所以
,即
,
.所以这两个内角的度数分别是48°,72°.
20.
答案:证明:∵AB∥CD,
∴∠BEF+∠EFD=180°.
∵∠BEF和∠EFD的平分线交于点G,
∴
,
.
∴
.
∴∠G=90°.
∴EG⊥FG.
解析过程:
21.
答案:证明:∵∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角和),∠B=∠C(已知),
∴
(等式的性质).
∵AD平分∠EAC(已知),
∴∠
(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥BC(内错角相等,两直线平行).
解析过程::要证明AD∥BC,只需证明“同位角相等”或“内错角相等”或“同旁内角互补”.
22.
答案:见解析
解析过程:证明:∵∠DCB是△DCE的一个外角(外角定义)
∴∠DCB>∠CDE(三角形的一个外角大于任何一个和它不相邻的内角)
∵∠ADB是△BCD的一个外角(外角定义)
∴∠ADB>∠DCB(三角形的一个外角大于任何一个和它不相邻的内角)
∴∠ADB>∠CDE(不等式的性质).
23.
答案:
,
解析过程:∵BD是
的平分线,∴
。
∵
,∴
。
∴
。设
,
由
,得
,解得
。∴
,
24.
答案:24°
解析过程:∵∠1=∠2,∠3=∠4,∠3=∠1+∠2,
∴2∠2=∠4,
∵∠2+∠4+∠BAC=180°,
∴∠2+2∠2+63°=180°,
∴3∠2+63°=180°
∴∠1=∠2=39°,
∠DAC=∠BAC-∠1=63°-39°=24°。
25.
答案:(1)25° (2)30° (3)35° (4)50° (5)
(6)∵∠ACD=∠ACP+
∠PCD=∠A+
∠ABC,∠ACP=∠PCD,∠ABP=∠PBC,∴2∠PCD=∠A+
2∠PBC.∵∠PCD=∠P+∠PBC,∴2(∠P+∠PBC)=∠A+2∠PBC.∴
.
