湘教版九年级数学上册周周清检测内容3.5-3.6试卷(word版含答案)
文档属性
| 名称 | 湘教版九年级数学上册周周清检测内容3.5-3.6试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 13:21:58 | ||
图片预览

文档简介
检测内容:3.5-3.6
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共28分)
1.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=OD′,则A′B′∶AB为(
)
A.2∶3
B.3∶2
C.1∶2
D.2∶1
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(
)
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
3.如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10,则零件的内孔直径AB长为(
)
A.30
B.20
C.10
D.5
4.(防城港中考)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,则△A′B′C′的面积是(
)
A.3
B.6
C.9
D.12
5.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,
光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知
AB⊥BD,CD⊥BD,
且测得AB=1.2米,
BP=1.8米,
PD=12米,那么该古城墙的高度是(
)
A.6米
B.8米
C.18米
D.24米
6.(2019·郴州改编)已知A
(4,2),B(2,-2),以点O为位似中心,按位似比1∶2把△ABO缩小,则点A的对应点A′的坐标为(
)
A.(-2,-1)
B.(2,1)或(-2,-1)
C.(3,1)或(-3,-1)
D.(3,1)
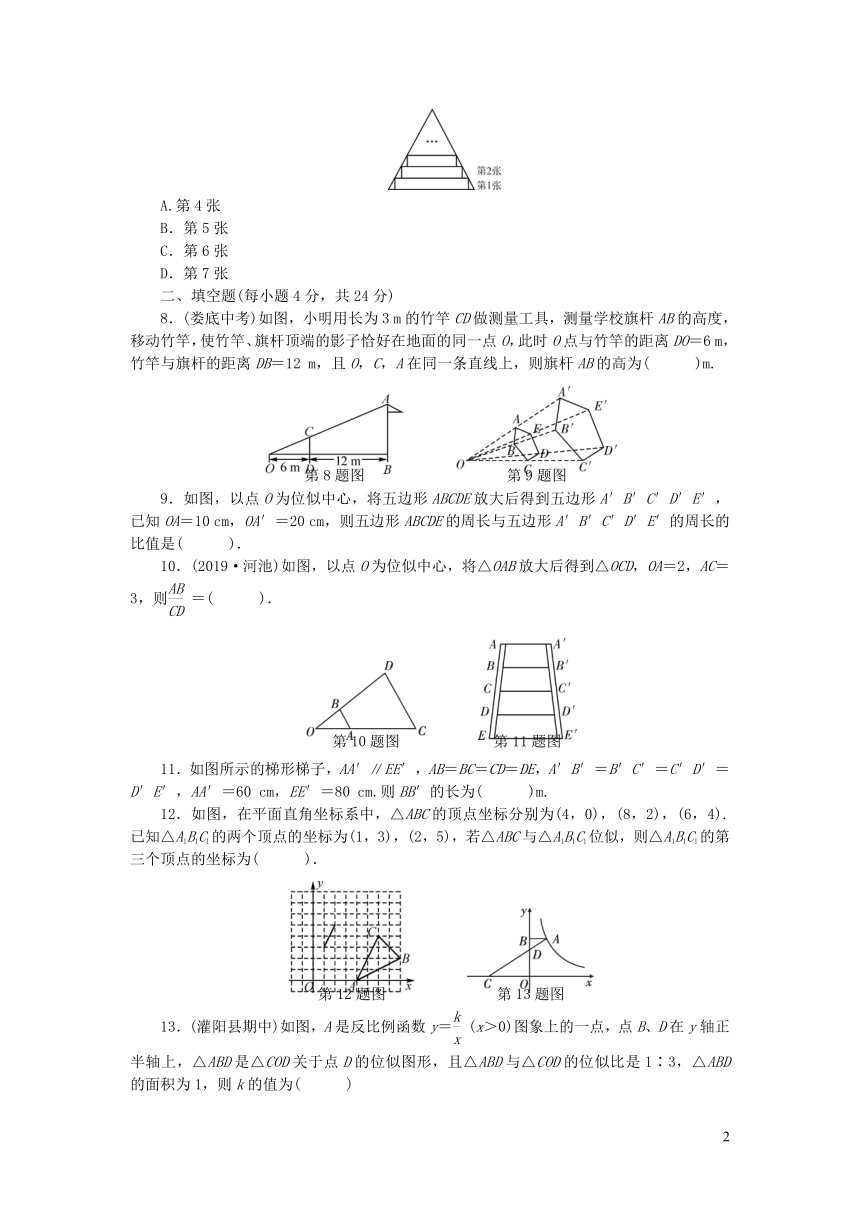
7.一张等腰三角形纸片,底边长15
cm,底边上的高长22.5
cm,现沿底边依次从下往上裁剪宽度均为3
cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题(每小题4分,共24分)
8.(娄底中考)如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离DO=6
m,竹竿与旗杆的距离DB=12
m,且O,C,A在同一条直线上,则旗杆AB的高为(
)m.
9.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是(
).
10.(2019·河池)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=(
).
11.如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60
cm,EE′=80
cm.则BB′的长为(
)m.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为(
).
13.(灌阳县期中)如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1∶3,△ABD的面积为1,则k的值为(
)
三、解答题(共48分)
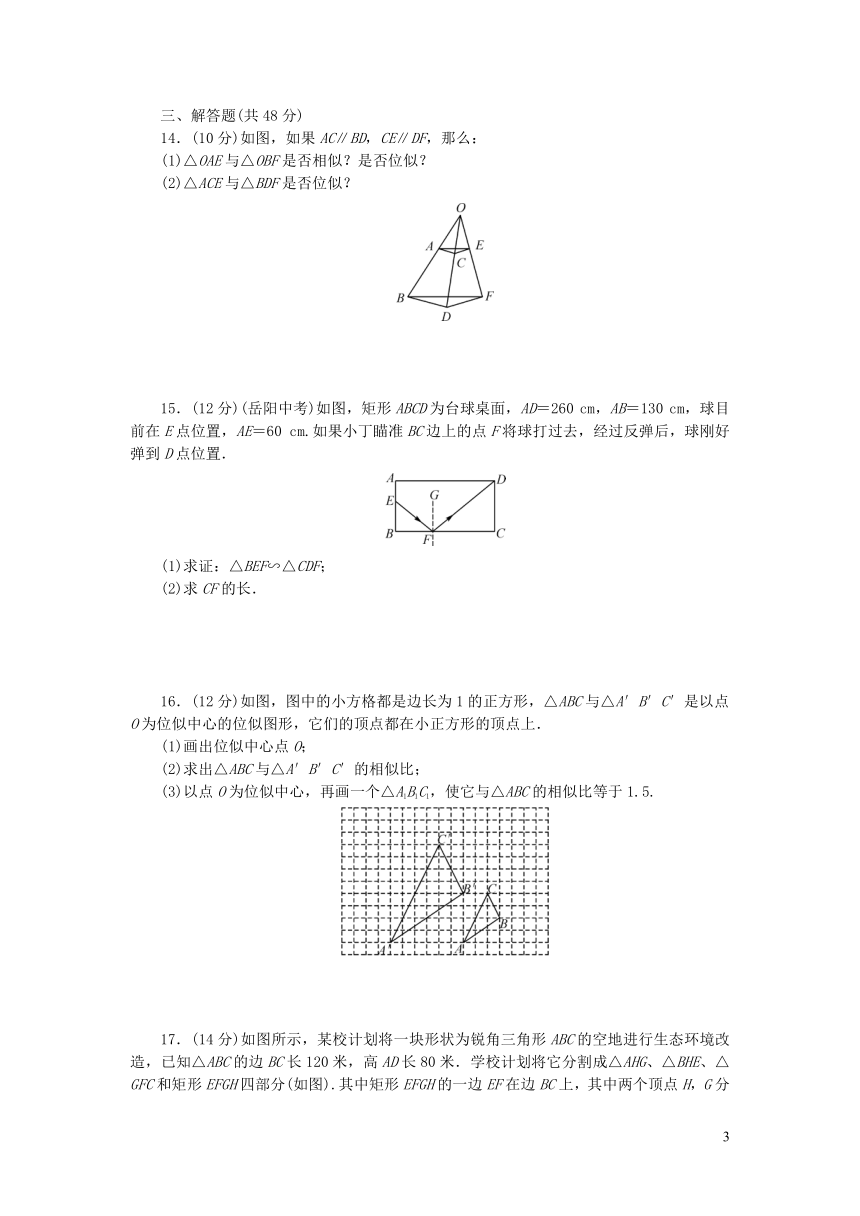
14.(10分)如图,如果AC∥BD,CE∥DF,那么:
(1)△OAE与△OBF是否相似?是否位似?
(2)△ACE与△BDF是否位似?
15.(12分)(岳阳中考)如图,矩形ABCD为台球桌面,AD=260
cm,AB=130
cm,球目前在E点位置,AE=60
cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
16.(12分)如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
17.(14分)如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造,已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上,其中两个顶点H,G分别在边AB,AC上,AD垂直BC于点D,交GH于点K,现计划在△AHG上种草,在△BHE,△GFC上都种花.在矩形EFGH上兴建喷泉,当FG长为多少米时,种草的面积与种花的面积相等?
检测内容:3.5-3.6(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共28分)
1.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=OD′,则A′B′∶AB为(D)
A.2∶3
B.3∶2
C.1∶2
D.2∶1
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(C)
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
3.如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10,则零件的内孔直径AB长为(B)
A.30
B.20
C.10
D.5
4.(防城港中考)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,则△A′B′C′的面积是(D)
A.3
B.6
C.9
D.12
5.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,
光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知
AB⊥BD,CD⊥BD,
且测得AB=1.2米,
BP=1.8米,
PD=12米,那么该古城墙的高度是(B)
A.6米
B.8米
C.18米
D.24米
6.(2019·郴州改编)已知A
(4,2),B(2,-2),以点O为位似中心,按位似比1∶2把△ABO缩小,则点A的对应点A′的坐标为(B)
A.(-2,-1)
B.(2,1)或(-2,-1)
C.(3,1)或(-3,-1)
D.(3,1)
7.一张等腰三角形纸片,底边长15
cm,底边上的高长22.5
cm,现沿底边依次从下往上裁剪宽度均为3
cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(C)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题(每小题4分,共24分)
8.(娄底中考)如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离DO=6
m,竹竿与旗杆的距离DB=12
m,且O,C,A在同一条直线上,则旗杆AB的高为__9__m.
9.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是__1∶2__.
10.(2019·河池)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=.
11.如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60
cm,EE′=80
cm.则BB′的长为__0.65__m.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为__(3,4)或(0,4)__.
13.(灌阳县期中)如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1∶3,△ABD的面积为1,则k的值为8.
三、解答题(共48分)
14.(10分)如图,如果AC∥BD,CE∥DF,那么:
(1)△OAE与△OBF是否相似?是否位似?
(2)△ACE与△BDF是否位似?
解:(1)△OAE与△OBF相似且位似,理由:∵AC∥BD,∴∠OAC=∠OBD,又∠AOC=∠BOD,∴△OAC∽△OBD,∴=,同理得=,∴=,∵∠AOE=∠BOF,∴△OAE∽△OBF,又△AOE与△BOF各对应点的连线都经过点O,∴△OAE与△OBF位似;(2)△ACE与△BDF位似.
15.(12分)(岳阳中考)如图,矩形ABCD为台球桌面,AD=260
cm,AB=130
cm,球目前在E点位置,AE=60
cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
解:(1)证明:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,∴△BEF∽△CDF;(2)由(1)知,△BEF∽△CDF,∴=,即=,解得CF=169.即CF的长度是169
cm.
16.(12分)如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
解:(1)略;(2)相似比为1∶2;(3)略.
17.(14分)如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造,已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上,其中两个顶点H,G分别在边AB,AC上,AD垂直BC于点D,交GH于点K,现计划在△AHG上种草,在△BHE,△GFC上都种花.在矩形EFGH上兴建喷泉,当FG长为多少米时,种草的面积与种花的面积相等?
解:设FG=x米,则AK=(80-x)米.由△AHG∽△ABC,BC=120,AD=80,可得:=,∴HG=120-x,BE+FC=120-(120-x)=x,∴·(120-x)·(80-x)=×x·x,解得x=40,∴当FG的长为40米时,种草的面积和种花的面积相等.
1
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共28分)
1.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=OD′,则A′B′∶AB为(
)
A.2∶3
B.3∶2
C.1∶2
D.2∶1
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(
)
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
3.如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10,则零件的内孔直径AB长为(
)
A.30
B.20
C.10
D.5
4.(防城港中考)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,则△A′B′C′的面积是(
)
A.3
B.6
C.9
D.12
5.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,
光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知
AB⊥BD,CD⊥BD,
且测得AB=1.2米,
BP=1.8米,
PD=12米,那么该古城墙的高度是(
)
A.6米
B.8米
C.18米
D.24米
6.(2019·郴州改编)已知A
(4,2),B(2,-2),以点O为位似中心,按位似比1∶2把△ABO缩小,则点A的对应点A′的坐标为(
)
A.(-2,-1)
B.(2,1)或(-2,-1)
C.(3,1)或(-3,-1)
D.(3,1)
7.一张等腰三角形纸片,底边长15
cm,底边上的高长22.5
cm,现沿底边依次从下往上裁剪宽度均为3
cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题(每小题4分,共24分)
8.(娄底中考)如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离DO=6
m,竹竿与旗杆的距离DB=12
m,且O,C,A在同一条直线上,则旗杆AB的高为(
)m.
9.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是(
).
10.(2019·河池)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=(
).
11.如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60
cm,EE′=80
cm.则BB′的长为(
)m.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为(
).
13.(灌阳县期中)如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1∶3,△ABD的面积为1,则k的值为(
)
三、解答题(共48分)
14.(10分)如图,如果AC∥BD,CE∥DF,那么:
(1)△OAE与△OBF是否相似?是否位似?
(2)△ACE与△BDF是否位似?
15.(12分)(岳阳中考)如图,矩形ABCD为台球桌面,AD=260
cm,AB=130
cm,球目前在E点位置,AE=60
cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
16.(12分)如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
17.(14分)如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造,已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上,其中两个顶点H,G分别在边AB,AC上,AD垂直BC于点D,交GH于点K,现计划在△AHG上种草,在△BHE,△GFC上都种花.在矩形EFGH上兴建喷泉,当FG长为多少米时,种草的面积与种花的面积相等?
检测内容:3.5-3.6(答案版)
得分________ 卷后分________ 评价________
一、选择题(每小题4分,共28分)
1.如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,O为位似中心,OD=OD′,则A′B′∶AB为(D)
A.2∶3
B.3∶2
C.1∶2
D.2∶1
2.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(C)
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
3.如图,用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10,则零件的内孔直径AB长为(B)
A.30
B.20
C.10
D.5
4.(防城港中考)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1∶2,已知△ABC的面积是3,则△A′B′C′的面积是(D)
A.3
B.6
C.9
D.12
5.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,
光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知
AB⊥BD,CD⊥BD,
且测得AB=1.2米,
BP=1.8米,
PD=12米,那么该古城墙的高度是(B)
A.6米
B.8米
C.18米
D.24米
6.(2019·郴州改编)已知A
(4,2),B(2,-2),以点O为位似中心,按位似比1∶2把△ABO缩小,则点A的对应点A′的坐标为(B)
A.(-2,-1)
B.(2,1)或(-2,-1)
C.(3,1)或(-3,-1)
D.(3,1)
7.一张等腰三角形纸片,底边长15
cm,底边上的高长22.5
cm,现沿底边依次从下往上裁剪宽度均为3
cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(C)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题(每小题4分,共24分)
8.(娄底中考)如图,小明用长为3
m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时O点与竹竿的距离DO=6
m,竹竿与旗杆的距离DB=12
m,且O,C,A在同一条直线上,则旗杆AB的高为__9__m.
9.如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10
cm,OA′=20
cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是__1∶2__.
10.(2019·河池)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=.
11.如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=60
cm,EE′=80
cm.则BB′的长为__0.65__m.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为__(3,4)或(0,4)__.
13.(灌阳县期中)如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1∶3,△ABD的面积为1,则k的值为8.
三、解答题(共48分)
14.(10分)如图,如果AC∥BD,CE∥DF,那么:
(1)△OAE与△OBF是否相似?是否位似?
(2)△ACE与△BDF是否位似?
解:(1)△OAE与△OBF相似且位似,理由:∵AC∥BD,∴∠OAC=∠OBD,又∠AOC=∠BOD,∴△OAC∽△OBD,∴=,同理得=,∴=,∵∠AOE=∠BOF,∴△OAE∽△OBF,又△AOE与△BOF各对应点的连线都经过点O,∴△OAE与△OBF位似;(2)△ACE与△BDF位似.
15.(12分)(岳阳中考)如图,矩形ABCD为台球桌面,AD=260
cm,AB=130
cm,球目前在E点位置,AE=60
cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
解:(1)证明:如图,在矩形ABCD中:∠DFC=∠EFB,∠EBF=∠FCD=90°,∴△BEF∽△CDF;(2)由(1)知,△BEF∽△CDF,∴=,即=,解得CF=169.即CF的长度是169
cm.
16.(12分)如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
解:(1)略;(2)相似比为1∶2;(3)略.
17.(14分)如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造,已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上,其中两个顶点H,G分别在边AB,AC上,AD垂直BC于点D,交GH于点K,现计划在△AHG上种草,在△BHE,△GFC上都种花.在矩形EFGH上兴建喷泉,当FG长为多少米时,种草的面积与种花的面积相等?
解:设FG=x米,则AK=(80-x)米.由△AHG∽△ABC,BC=120,AD=80,可得:=,∴HG=120-x,BE+FC=120-(120-x)=x,∴·(120-x)·(80-x)=×x·x,解得x=40,∴当FG的长为40米时,种草的面积和种花的面积相等.
1
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
