28.1圆的概念及性质-冀教版九年级数学上册课件(共29张PPT)
文档属性
| 名称 | 28.1圆的概念及性质-冀教版九年级数学上册课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 19:26:01 | ||
图片预览







文档简介
(共29张PPT)
28.1
圆的概念及性质
冀教版九上
第二十八章
圆
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.以生活为基础,建立圆的概念.
2.探究圆的对称性.
3.理解圆、弧、弦、优弧、劣弧、半圆、等圆、等弧的概念.
创设情境,引入新课
日常生活中,有许多物品是圆形的,例如轮胎.
创设情境,引入新课
为什么轮胎一定要做成圆形的?假如轮胎不是圆形的,会怎样呢?
圆形轮胎上的每个点到圆中心的距离相等,轮胎滚动时能保持平稳.
颠簸得很厉害
创设情境,引入新课
靶子为什么做成圆形?
同一个圆环上的点到中心的距离是一样的,可以保证射中的几率相同,更公平.
创设情境,引入新课
观察你手边的水杯,水杯的截面还有水杯盖都是圆形的?这是为什么呢?
圆形水杯盖,随手拿起从任何位置都可以快速盖住,且杯盖没有落入杯中的可能.
假如是正方形杯盖,对好位置才能盖上,且正方形的对角线大于边长,杯盖有落入杯中的可能.
创设情境,引入新课
生活中的圆还有很多很多,这些圆的特征是什么?你会描述出来吗?
新课学习
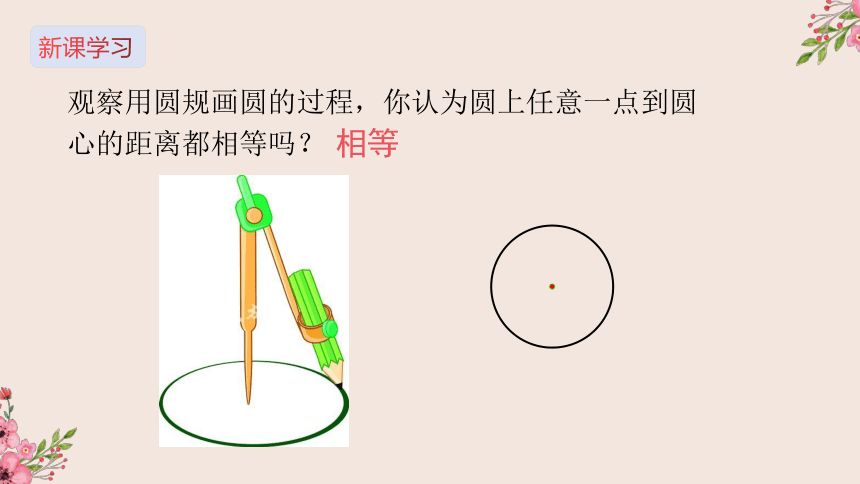
观察用圆规画圆的过程,你认为圆上任意一点到圆心的距离都相等吗?
相等
·
新课学习
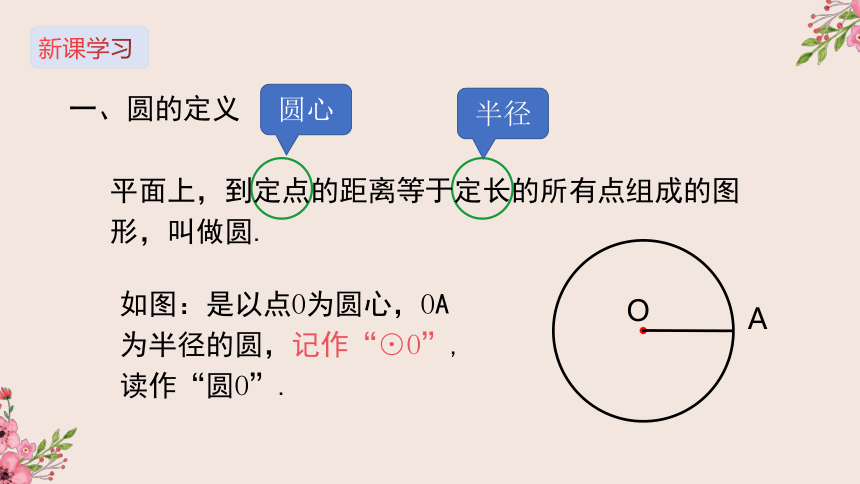
一、圆的定义
平面上,到定点的距离等于定长的所有点组成的图形,叫做圆.
●
O
A
圆心
半径
如图:是以点O为圆心,OA为半径的圆,记作“⊙O”,读作“圆O”.
巩固小练习
问题:矩形ABCD的四个顶点在同一个圆上吗?
O
D
C
B
A
小美
圆上的所有点到圆心的距离相等,反过来,到同一点距离相等的点在同一个圆上.
分析:连接AC、BD交于点O,由矩形性质可得,OA=OB=OC=OD.则点A、B、C、D在以点O为圆心OA为半径的圆上.
新课学习
二、确定一个圆的条件
圆心
半径
决定圆的位置
决定圆的大小
巩固小练习
下列说法中,错误的是________.
①经过点P的圆有无数个;
②以点P为圆心的圆有无数个;
③半径为3cm,且经过点P的圆有无数个;
④以点P为圆心,3cm为半径的圆有无数个.
④
新课学习
三、圆的对称性
将圆沿一条直径所在的直线对折,两旁的部分可以重合.
圆是轴对称图形,对称轴是直径所在的直线.
新课学习
三、圆的对称性
圆是中心对称图形,对称中心是圆心.
●
将圆绕圆心旋转180°后,与自身重合.
圆绕圆心旋转任意角度后都与自身重合.
巩固小练习
如图,正方形中放了一个最大的圆,若正方形的边长为6cm,则图中阴影部分的面积为_____.
18
新课学习
四、圆的有关概念
连接圆上任意两点的线段(如图AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦
直径是圆中最长的弦.
·
C
O
A
B
新课学习
四、圆的有关概念
2.弧
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
圆上任意两点间的部分叫做圆弧,简称弧.
半圆ACB:不含直径
A
B
C
A
B
C
弓形ACB:含直径
新课学习
小于半圆的弧(如图中的AC)叫做劣弧.读作“弧AC”
⌒
大于半圆的弧(用三点表示,如图中的ABC)叫做优弧.读作“弧ABC”
⌒
四、圆的有关概念
3.优弧和劣弧
·
C
O
A
B
新课学习
能够完全重合的两个圆叫做等圆.
4.等圆
圆心不同,半径相等.
四、圆的有关概念
新课学习
5.等弧
能够完全重合的两条弧叫做等弧.
四、圆的有关概念
●
●
●
●
A
B
C
D
AB与CD是等弧,存在于等圆中.
⌒
⌒
新课学习
5.等弧
能够完全重合的两条弧叫做等弧.
四、圆的有关概念
A
B
C
D
AB与CD是等弧,存在于同圆中.
⌒
⌒
巩固小练习
A
B
C
O
1.如图,点O为⊙OD的圆心,点A、B、C在⊙O上.
⊙O的半径有___条,是_________.
⊙O的弦有___条,是__________.
图中劣弧有___条,是________.
优弧有___条,是___________.
图中有___条直径,____个半圆.
3
OA、OB、OC
3
AB、BC、AC
2
AB、BC、
⌒
⌒
2
ACB、BAC、
⌒
⌒
1
2
巩固小练习
A
B
C
O
1.如图,点O为⊙OD的圆心,点A、B、C在⊙O上.
注意:
在圆中,一条弦对___条弧,一条是_____,另一条是_____,或者两条弧都是______.
2
劣弧
优弧
半圆
巩固小练习
2.下列说法中,不正确的是(
).
A.过圆心的弦是圆的直径.
B.等弧的长度一定相等.
C.周长相等的两个圆是等圆.
D.同一条弦所对的两条弧一定是等弧.
D
巩固小练习
3.下列命题中,正确的有(
)个.
①直径是弦,但弦不一定是直径;
②半圆是弧,但弧不一定是半圆;
③半径相等的两个圆是等圆;
④一条弦把圆分成的两段弧中,至少有一条优弧;
⑤长度相等的两条弧是等弧.
3
巩固小练习
4.已知A、B是半径为5的⊙O上两个不同的点,则弦AB的取值范围是_______.
5.过圆上一点可以作圆的最长弦有_____
条.
过圆内一点A可以作出圆的最长弦有_________条.
0<AB<10
1
1条或无数
灵活运用,拓展思维
1.如图,O为两同心圆的圆心,点A为大圆上的点,点B为小圆上的一点,且∠ABO=90°,AB=3,则该圆环的面积为_______.
A
O
B
O
9π
灵活运用,拓展思维
2.如图,在△ABC中,点D是∠BAC的平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E,求证:A、B、D三点在以点E为圆心的圆上.
E
D
C
B
A
分析:只需证明EA=EB=ED
同学们再见
28.1
圆的概念及性质
冀教版九上
第二十八章
圆
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.以生活为基础,建立圆的概念.
2.探究圆的对称性.
3.理解圆、弧、弦、优弧、劣弧、半圆、等圆、等弧的概念.
创设情境,引入新课
日常生活中,有许多物品是圆形的,例如轮胎.
创设情境,引入新课
为什么轮胎一定要做成圆形的?假如轮胎不是圆形的,会怎样呢?
圆形轮胎上的每个点到圆中心的距离相等,轮胎滚动时能保持平稳.
颠簸得很厉害
创设情境,引入新课
靶子为什么做成圆形?
同一个圆环上的点到中心的距离是一样的,可以保证射中的几率相同,更公平.
创设情境,引入新课
观察你手边的水杯,水杯的截面还有水杯盖都是圆形的?这是为什么呢?
圆形水杯盖,随手拿起从任何位置都可以快速盖住,且杯盖没有落入杯中的可能.
假如是正方形杯盖,对好位置才能盖上,且正方形的对角线大于边长,杯盖有落入杯中的可能.
创设情境,引入新课
生活中的圆还有很多很多,这些圆的特征是什么?你会描述出来吗?
新课学习
观察用圆规画圆的过程,你认为圆上任意一点到圆心的距离都相等吗?
相等
·
新课学习
一、圆的定义
平面上,到定点的距离等于定长的所有点组成的图形,叫做圆.
●
O
A
圆心
半径
如图:是以点O为圆心,OA为半径的圆,记作“⊙O”,读作“圆O”.
巩固小练习
问题:矩形ABCD的四个顶点在同一个圆上吗?
O
D
C
B
A
小美
圆上的所有点到圆心的距离相等,反过来,到同一点距离相等的点在同一个圆上.
分析:连接AC、BD交于点O,由矩形性质可得,OA=OB=OC=OD.则点A、B、C、D在以点O为圆心OA为半径的圆上.
新课学习
二、确定一个圆的条件
圆心
半径
决定圆的位置
决定圆的大小
巩固小练习
下列说法中,错误的是________.
①经过点P的圆有无数个;
②以点P为圆心的圆有无数个;
③半径为3cm,且经过点P的圆有无数个;
④以点P为圆心,3cm为半径的圆有无数个.
④
新课学习
三、圆的对称性
将圆沿一条直径所在的直线对折,两旁的部分可以重合.
圆是轴对称图形,对称轴是直径所在的直线.
新课学习
三、圆的对称性
圆是中心对称图形,对称中心是圆心.
●
将圆绕圆心旋转180°后,与自身重合.
圆绕圆心旋转任意角度后都与自身重合.
巩固小练习
如图,正方形中放了一个最大的圆,若正方形的边长为6cm,则图中阴影部分的面积为_____.
18
新课学习
四、圆的有关概念
连接圆上任意两点的线段(如图AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦
直径是圆中最长的弦.
·
C
O
A
B
新课学习
四、圆的有关概念
2.弧
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
圆上任意两点间的部分叫做圆弧,简称弧.
半圆ACB:不含直径
A
B
C
A
B
C
弓形ACB:含直径
新课学习
小于半圆的弧(如图中的AC)叫做劣弧.读作“弧AC”
⌒
大于半圆的弧(用三点表示,如图中的ABC)叫做优弧.读作“弧ABC”
⌒
四、圆的有关概念
3.优弧和劣弧
·
C
O
A
B
新课学习
能够完全重合的两个圆叫做等圆.
4.等圆
圆心不同,半径相等.
四、圆的有关概念
新课学习
5.等弧
能够完全重合的两条弧叫做等弧.
四、圆的有关概念
●
●
●
●
A
B
C
D
AB与CD是等弧,存在于等圆中.
⌒
⌒
新课学习
5.等弧
能够完全重合的两条弧叫做等弧.
四、圆的有关概念
A
B
C
D
AB与CD是等弧,存在于同圆中.
⌒
⌒
巩固小练习
A
B
C
O
1.如图,点O为⊙OD的圆心,点A、B、C在⊙O上.
⊙O的半径有___条,是_________.
⊙O的弦有___条,是__________.
图中劣弧有___条,是________.
优弧有___条,是___________.
图中有___条直径,____个半圆.
3
OA、OB、OC
3
AB、BC、AC
2
AB、BC、
⌒
⌒
2
ACB、BAC、
⌒
⌒
1
2
巩固小练习
A
B
C
O
1.如图,点O为⊙OD的圆心,点A、B、C在⊙O上.
注意:
在圆中,一条弦对___条弧,一条是_____,另一条是_____,或者两条弧都是______.
2
劣弧
优弧
半圆
巩固小练习
2.下列说法中,不正确的是(
).
A.过圆心的弦是圆的直径.
B.等弧的长度一定相等.
C.周长相等的两个圆是等圆.
D.同一条弦所对的两条弧一定是等弧.
D
巩固小练习
3.下列命题中,正确的有(
)个.
①直径是弦,但弦不一定是直径;
②半圆是弧,但弧不一定是半圆;
③半径相等的两个圆是等圆;
④一条弦把圆分成的两段弧中,至少有一条优弧;
⑤长度相等的两条弧是等弧.
3
巩固小练习
4.已知A、B是半径为5的⊙O上两个不同的点,则弦AB的取值范围是_______.
5.过圆上一点可以作圆的最长弦有_____
条.
过圆内一点A可以作出圆的最长弦有_________条.
0<AB<10
1
1条或无数
灵活运用,拓展思维
1.如图,O为两同心圆的圆心,点A为大圆上的点,点B为小圆上的一点,且∠ABO=90°,AB=3,则该圆环的面积为_______.
A
O
B
O
9π
灵活运用,拓展思维
2.如图,在△ABC中,点D是∠BAC的平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E,求证:A、B、D三点在以点E为圆心的圆上.
E
D
C
B
A
分析:只需证明EA=EB=ED
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
