28.2过三点的圆-冀教版九年级数学上册课件(共30张PPT)
文档属性
| 名称 | 28.2过三点的圆-冀教版九年级数学上册课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
28.2
过三点的圆
冀教版九上
第二十八章
圆
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.探究在平面内经过几个点可以确定一个圆.
2.知道“不在同一直线上的三个点确定一个圆”.
3.知道三角形的外接圆、外心的概念,会用尺规画三角形的外接圆.
创设情境,引入新课
我们知道,经过一个点可以画无数条直线,经过两个点的直线有且只有一条,即两点确定一条直线,那么几个点可以确定一个圆呢?
●
●
●
创设情境,引入新课
确定一个圆的条件是什么?
圆心和半径
试一试:在练习本上画点A,经过点A作圆,能作几个?你是怎样确定圆心和半径的?
●
A
●
O
以平面上除A点外任意一点为圆心,
以此点与A点之间的距离为半径作圆.
创设情境,引入新课
A
经过平面上一点作圆,圆心不确定,半径不确定,
故可做无数圆.
即平面上一个点不能确定一个圆.
我们再来试试过两个点作圆......
创设情境,引入新课
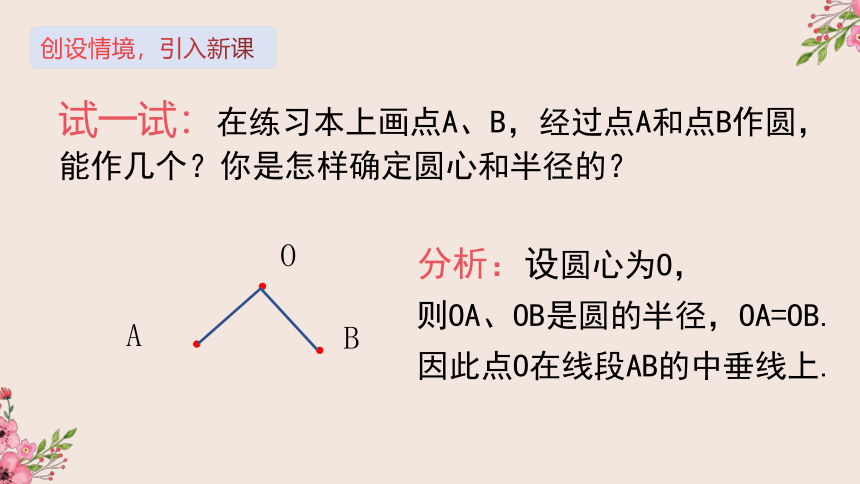
试一试:在练习本上画点A、B,经过点A和点B作圆,能作几个?你是怎样确定圆心和半径的?
分析:设圆心为O,
则OA、OB是圆的半径,OA=OB.
因此点O在线段AB的中垂线上.
●
●
B
A
●
O
创设情境,引入新课
●
●
B
A
●
O
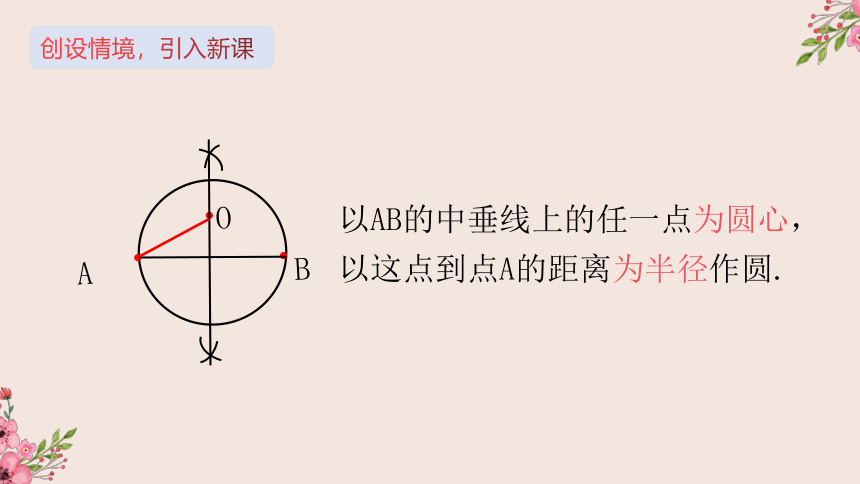
以AB的中垂线上的任一点为圆心,以这点到点A的距离为半径作圆.
创设情境,引入新课
·
·
·
O1
O2
·
·
O3
A
B
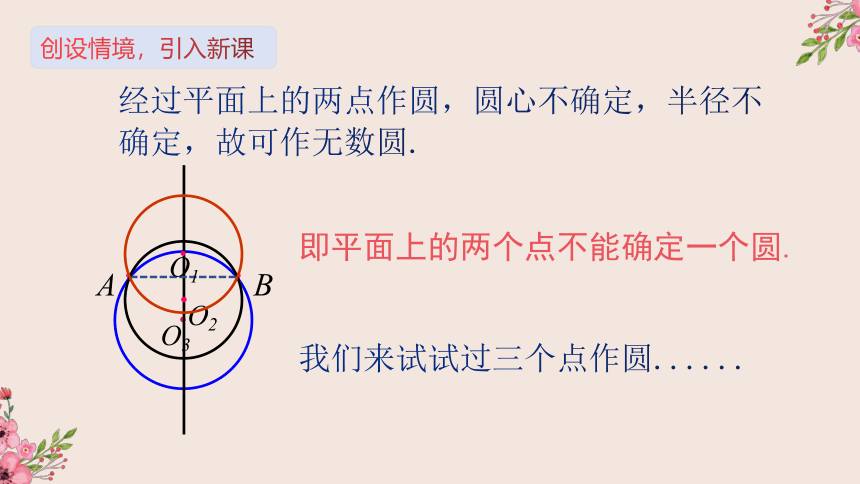
经过平面上的两点作圆,圆心不确定,半径不确定,故可作无数圆.
即平面上的两个点不能确定一个圆.
我们来试试过三个点作圆......
创设情境,引入新课
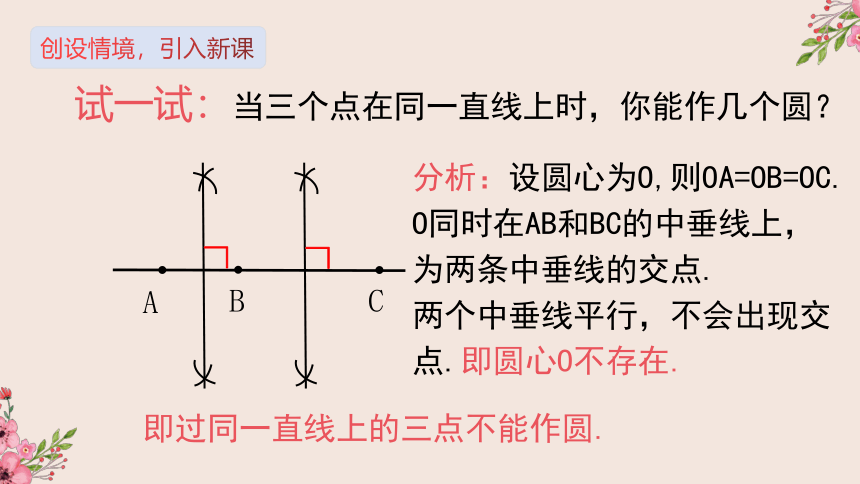
试一试:当三个点在同一直线上时,你能作几个圆?
●
●
●
A
B
C
分析:设圆心为O,则OA=OB=OC.
O同时在AB和BC的中垂线上,为两条中垂线的交点.
两个中垂线平行,不会出现交点.即圆心O不存在.
即过同一直线上的三点不能作圆.
∟
∟
创设情境,引入新课
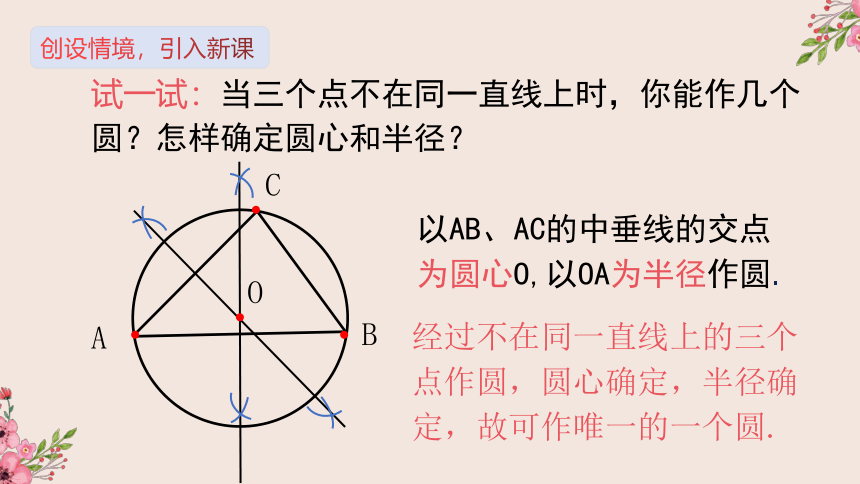
试一试:当三个点不在同一直线上时,你能作几个圆?怎样确定圆心和半径?
O
C
B
A
●
●
●
●
以AB、AC的中垂线的交点为圆心O,以OA为半径作圆.
经过不在同一直线上的三个点作圆,圆心确定,半径确定,故可作唯一的一个圆.
新课学习
不在同一平面上的三个点确定一个圆.
知识点一:
知识点运用,巩固小练习
1.根据下列条件,过A、B、C三点能确定一个圆的是(
)
A.AB=2,BC=2,AC=4
B.AB=4.5,BC=5.5,AC=10
C.AB=4,BC=3,AC=5
D.AB=1,BC=2,AC=3
C
知识点运用,巩固小练习
2.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四点中的任意三个点,能画圆的个数是(
).
●
●
●
●
3个
三角形的三个顶点不在同一直线上,因此它们在同一个圆上.
三角形的三个顶点一定在同一个圆上吗?
想一想
O
●
C
B
A
①经过三角形三个顶点的圆,叫做三角形的外接圆.
②外接圆的圆心叫做三角形的外心.
③三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆;点O是△ABC的外心;△ABC是⊙O的内接三角形.
知识点二:
O
●
C
B
A
④三角形的外心是
如图:点O是△ABC的外心;
则OA=OB=OC.
知识点二:
三角形三边的中垂线的交点
到三角形的三个顶点的距离相等.
用尺规作三角形的外接圆
③以EF和MN的交点O为圆心,以OA为半径作圆.
作法:①作线段AB的垂直平分线EF;
②作线段BC的垂直平分线MN;
⊙O即为△ABC的外接圆.
E
F
M
N
C
B
A
.O
知识点三:
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形
直角三角形
钝角三角形
分别画下面三角形的外接圆,并说明外心的位置与三角形的形状之间具有怎样的关系.(用尺规在课本151页练习第2题中画出)
外心在内部
外心在斜边中点
外心在外部
试一试
①三角形的外心位置
锐角三角形的外心位于三角形的内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形的外部.
结论:
②直角三角形外接圆的半径等于
斜边的一半
③等边三角形外接圆的半径等于
A
C
B
∟
∟
M
N
O
在等边△ABC中,设边长为a,两边的中垂线交于点O,则OB为外接圆半径
知识点运用,巩固小练习
1.下列命题中,是真命题的个数是_______.
①经过三点一定可以作圆;
②任意一个圆一定有且只有一个内接三角形;
③任意一个三角形一定有且只有一个外接圆;
④三角形的外心是三边中垂线的交点.
③④
知识点运用,巩固小练习
2.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用_____次就可以找到圆形工件的圆心.
N
M
B
A
2
分析:圆中两条不平行的弦的中垂线的交点即为圆心.
知识点运用,巩固小练习
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
A.点P
B.点Q
C.点R
D.点M
B
分析:AB、BC的中垂线的交点即为圆心.
知识点运用,巩固小练习
4.在等边ABC中,AB=6,则这个等边三角形的外接圆半径为_______.
知识点:
典例精析
例1.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述是否正确.
E
D
O
C
B
A
①O是△AEB的外心,O不是△AED的外心;
分析:判断O是不是△AEB的外心,就是判断OA=OE=OB是否成立;同理判断OA=OE=OD是否成立,可知O是不是△AED的外心.
由O是△ABC的外心,可得OA=OB=OC,由四边形OCDE为正方形,可得OE=OC.
因此,OA=OB=OE.
√
由于OE、OD分别是正方形OCDE的边和对角线
∴OE≠OD
∴O不是△AED的外心
√
√
典例精析
例1.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述是否正确.
E
D
O
C
B
A
②O是△ADB的外心,O不是△ADC的外心;
分析:由OA=OB≠OD
可得O不是△ADB的外心.
×
×
典例精析
例2.如图,小明家的房前有一块矩形的空地.空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来.(尺规作图,保留痕迹)
C
B
A
O
分析:画△ABC的外接圆即可.
典例精析
例2.如图,小明家的房前有一块矩形的空地.空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(2)若△ABC中,AB=8米,AC=6米,∠BAC=90°求花坛的面积.
C
B
A
分析:利用勾股定理求出斜边BC的长为10米,则半径为5米,花坛面积为25π㎡.
回顾与总结
不在同一直线上的三个点确定一个圆
三角形的外接圆、外心的概念
三角形的外心的位置
特殊三角形的外接圆半径
锐角三角形
直角三角形
钝角三角形
直角三角形
等边三角形
内部
斜边中点
外部
同学们再见
28.2
过三点的圆
冀教版九上
第二十八章
圆
新课引入
新课学习
典例精析
测试小结
学
习
目
标
冀教版九上
1.探究在平面内经过几个点可以确定一个圆.
2.知道“不在同一直线上的三个点确定一个圆”.
3.知道三角形的外接圆、外心的概念,会用尺规画三角形的外接圆.
创设情境,引入新课
我们知道,经过一个点可以画无数条直线,经过两个点的直线有且只有一条,即两点确定一条直线,那么几个点可以确定一个圆呢?
●
●
●
创设情境,引入新课
确定一个圆的条件是什么?
圆心和半径
试一试:在练习本上画点A,经过点A作圆,能作几个?你是怎样确定圆心和半径的?
●
A
●
O
以平面上除A点外任意一点为圆心,
以此点与A点之间的距离为半径作圆.
创设情境,引入新课
A
经过平面上一点作圆,圆心不确定,半径不确定,
故可做无数圆.
即平面上一个点不能确定一个圆.
我们再来试试过两个点作圆......
创设情境,引入新课
试一试:在练习本上画点A、B,经过点A和点B作圆,能作几个?你是怎样确定圆心和半径的?
分析:设圆心为O,
则OA、OB是圆的半径,OA=OB.
因此点O在线段AB的中垂线上.
●
●
B
A
●
O
创设情境,引入新课
●
●
B
A
●
O
以AB的中垂线上的任一点为圆心,以这点到点A的距离为半径作圆.
创设情境,引入新课
·
·
·
O1
O2
·
·
O3
A
B
经过平面上的两点作圆,圆心不确定,半径不确定,故可作无数圆.
即平面上的两个点不能确定一个圆.
我们来试试过三个点作圆......
创设情境,引入新课
试一试:当三个点在同一直线上时,你能作几个圆?
●
●
●
A
B
C
分析:设圆心为O,则OA=OB=OC.
O同时在AB和BC的中垂线上,为两条中垂线的交点.
两个中垂线平行,不会出现交点.即圆心O不存在.
即过同一直线上的三点不能作圆.
∟
∟
创设情境,引入新课
试一试:当三个点不在同一直线上时,你能作几个圆?怎样确定圆心和半径?
O
C
B
A
●
●
●
●
以AB、AC的中垂线的交点为圆心O,以OA为半径作圆.
经过不在同一直线上的三个点作圆,圆心确定,半径确定,故可作唯一的一个圆.
新课学习
不在同一平面上的三个点确定一个圆.
知识点一:
知识点运用,巩固小练习
1.根据下列条件,过A、B、C三点能确定一个圆的是(
)
A.AB=2,BC=2,AC=4
B.AB=4.5,BC=5.5,AC=10
C.AB=4,BC=3,AC=5
D.AB=1,BC=2,AC=3
C
知识点运用,巩固小练习
2.如图,点A、B、C在同一条直线上,点D在直线AB外,过这四点中的任意三个点,能画圆的个数是(
).
●
●
●
●
3个
三角形的三个顶点不在同一直线上,因此它们在同一个圆上.
三角形的三个顶点一定在同一个圆上吗?
想一想
O
●
C
B
A
①经过三角形三个顶点的圆,叫做三角形的外接圆.
②外接圆的圆心叫做三角形的外心.
③三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆;点O是△ABC的外心;△ABC是⊙O的内接三角形.
知识点二:
O
●
C
B
A
④三角形的外心是
如图:点O是△ABC的外心;
则OA=OB=OC.
知识点二:
三角形三边的中垂线的交点
到三角形的三个顶点的距离相等.
用尺规作三角形的外接圆
③以EF和MN的交点O为圆心,以OA为半径作圆.
作法:①作线段AB的垂直平分线EF;
②作线段BC的垂直平分线MN;
⊙O即为△ABC的外接圆.
E
F
M
N
C
B
A
.O
知识点三:
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形
直角三角形
钝角三角形
分别画下面三角形的外接圆,并说明外心的位置与三角形的形状之间具有怎样的关系.(用尺规在课本151页练习第2题中画出)
外心在内部
外心在斜边中点
外心在外部
试一试
①三角形的外心位置
锐角三角形的外心位于三角形的内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形的外部.
结论:
②直角三角形外接圆的半径等于
斜边的一半
③等边三角形外接圆的半径等于
A
C
B
∟
∟
M
N
O
在等边△ABC中,设边长为a,两边的中垂线交于点O,则OB为外接圆半径
知识点运用,巩固小练习
1.下列命题中,是真命题的个数是_______.
①经过三点一定可以作圆;
②任意一个圆一定有且只有一个内接三角形;
③任意一个三角形一定有且只有一个外接圆;
④三角形的外心是三边中垂线的交点.
③④
知识点运用,巩固小练习
2.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用_____次就可以找到圆形工件的圆心.
N
M
B
A
2
分析:圆中两条不平行的弦的中垂线的交点即为圆心.
知识点运用,巩固小练习
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
A.点P
B.点Q
C.点R
D.点M
B
分析:AB、BC的中垂线的交点即为圆心.
知识点运用,巩固小练习
4.在等边ABC中,AB=6,则这个等边三角形的外接圆半径为_______.
知识点:
典例精析
例1.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述是否正确.
E
D
O
C
B
A
①O是△AEB的外心,O不是△AED的外心;
分析:判断O是不是△AEB的外心,就是判断OA=OE=OB是否成立;同理判断OA=OE=OD是否成立,可知O是不是△AED的外心.
由O是△ABC的外心,可得OA=OB=OC,由四边形OCDE为正方形,可得OE=OC.
因此,OA=OB=OE.
√
由于OE、OD分别是正方形OCDE的边和对角线
∴OE≠OD
∴O不是△AED的外心
√
√
典例精析
例1.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述是否正确.
E
D
O
C
B
A
②O是△ADB的外心,O不是△ADC的外心;
分析:由OA=OB≠OD
可得O不是△ADB的外心.
×
×
典例精析
例2.如图,小明家的房前有一块矩形的空地.空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来.(尺规作图,保留痕迹)
C
B
A
O
分析:画△ABC的外接圆即可.
典例精析
例2.如图,小明家的房前有一块矩形的空地.空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(2)若△ABC中,AB=8米,AC=6米,∠BAC=90°求花坛的面积.
C
B
A
分析:利用勾股定理求出斜边BC的长为10米,则半径为5米,花坛面积为25π㎡.
回顾与总结
不在同一直线上的三个点确定一个圆
三角形的外接圆、外心的概念
三角形的外心的位置
特殊三角形的外接圆半径
锐角三角形
直角三角形
钝角三角形
直角三角形
等边三角形
内部
斜边中点
外部
同学们再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
