2020-2021学年苏科版 八年级数学上册1章全等三角形章末复习训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版 八年级数学上册1章全等三角形章末复习训练卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览

文档简介
苏科版2020-2021八年级数学上册1章全等三角形章末复习训练卷(有答案)
一、选择题
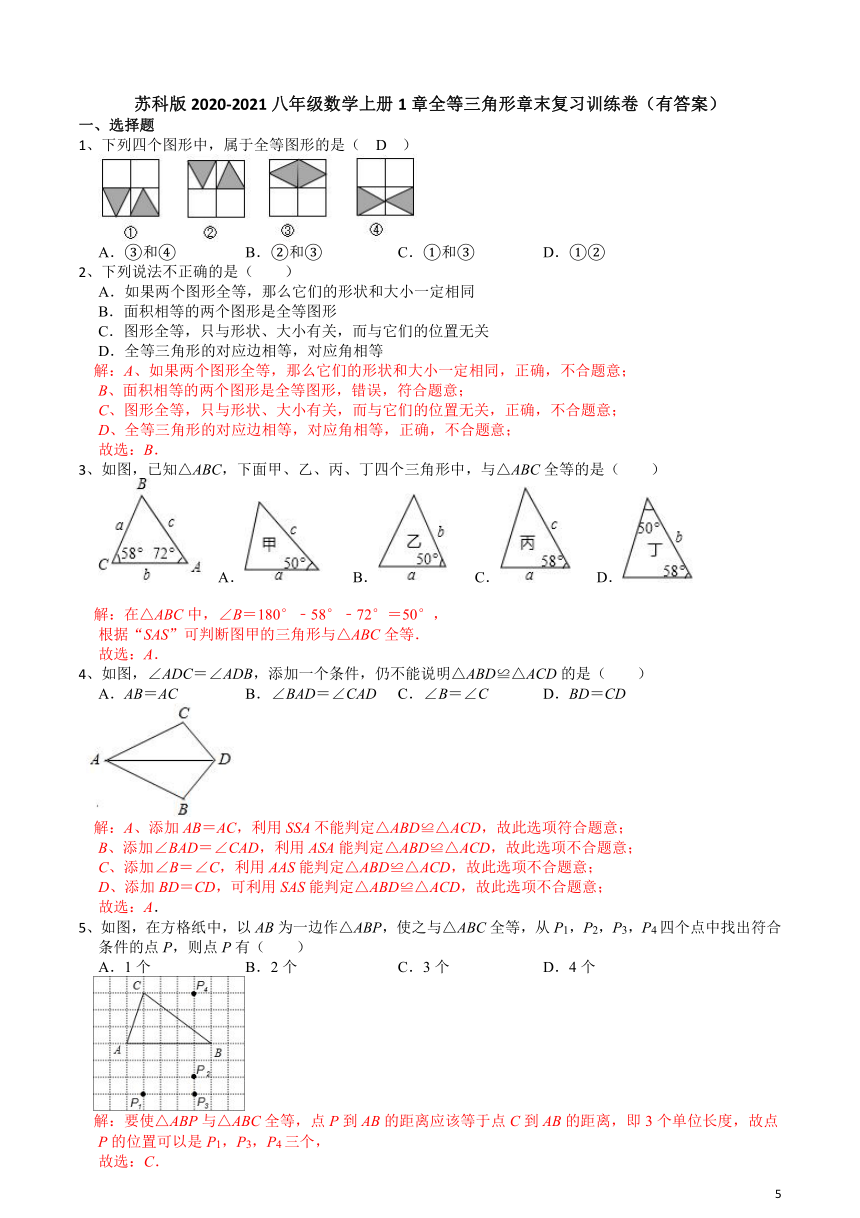
1、下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.①②
2、下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
3、如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.
B.
C.
D.
4、如图,∠ADC=∠ADB,添加一个条件,仍不能说明△ABD≌△ACD的是( )
A.AB=AC
B.∠BAD=∠CAD
C.∠B=∠C
D.BD=CD
(4题)
(5题)
5、如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
6、如图,已知AB=DE,∠B=∠E,添加下列哪个条件可以利用SAS判断△ABC≌△DEC.正确的是: .
①∠A=∠D;②BC=EC;③AC=DC;④∠BCE=∠ACD.
(6题)
(7题)
7、如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5
B.6
C.7
8、(2019秋江都区期中)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC?BD,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
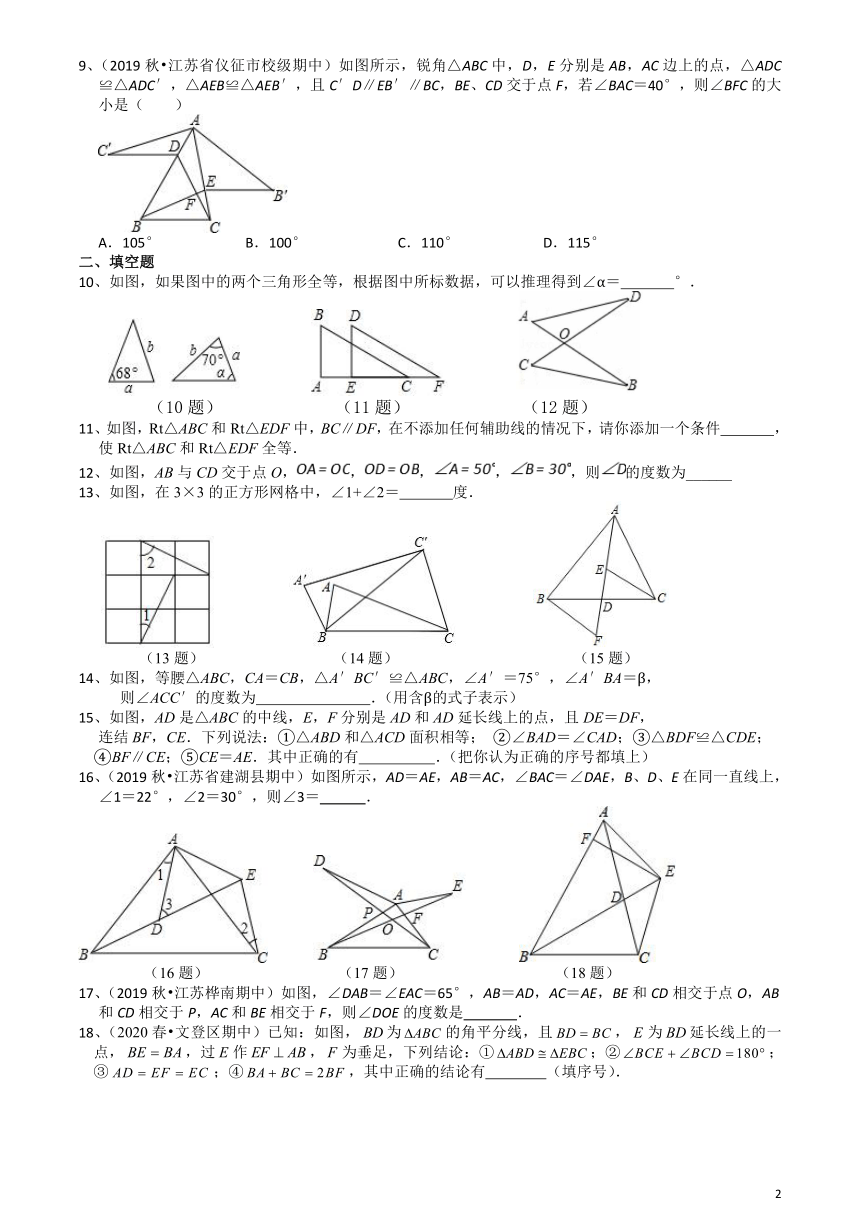
9、(2019秋?江苏省仪征市校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105°
B.100°
C.110°
D.115°
二、填空题
10、如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
(10题)
(11题)
(12题)
11、如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
12、如图,AB与CD交于点O,,,,,则的度数为______
13、如图,在3×3的正方形网格中,∠1+∠2=
度.
(13题)
(14题)
(15题)
14、如图,等腰△ABC,CA=CB,△A′BC′≌△ABC,∠A′=75°,∠A′BA=β,
则∠ACC′的度数为
.(用含β的式子表示)
15、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,
连结BF,CE.下列说法:①△ABD和△ACD面积相等;
②∠BAD=∠CAD;③△BDF≌△CDE;
④BF∥CE;⑤CE=AE.其中正确的有
.(把你认为正确的序号都填上)
16、(2019秋?江苏省建湖县期中)如图所示,AD=AE,AB=AC,∠BAC=∠DAE,B、D、E在同一直线上,∠1=22°,∠2=30°,则∠3=
.
(16题)
(17题)
(18题)
17、(2019秋?江苏桦南期中)如图,∠DAB=∠EAC=65°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是
.
18、(2020春?文登区期中)已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足,下列结论:①;②;
③;④,其中正确的结论有
(填序号).
三、解答题
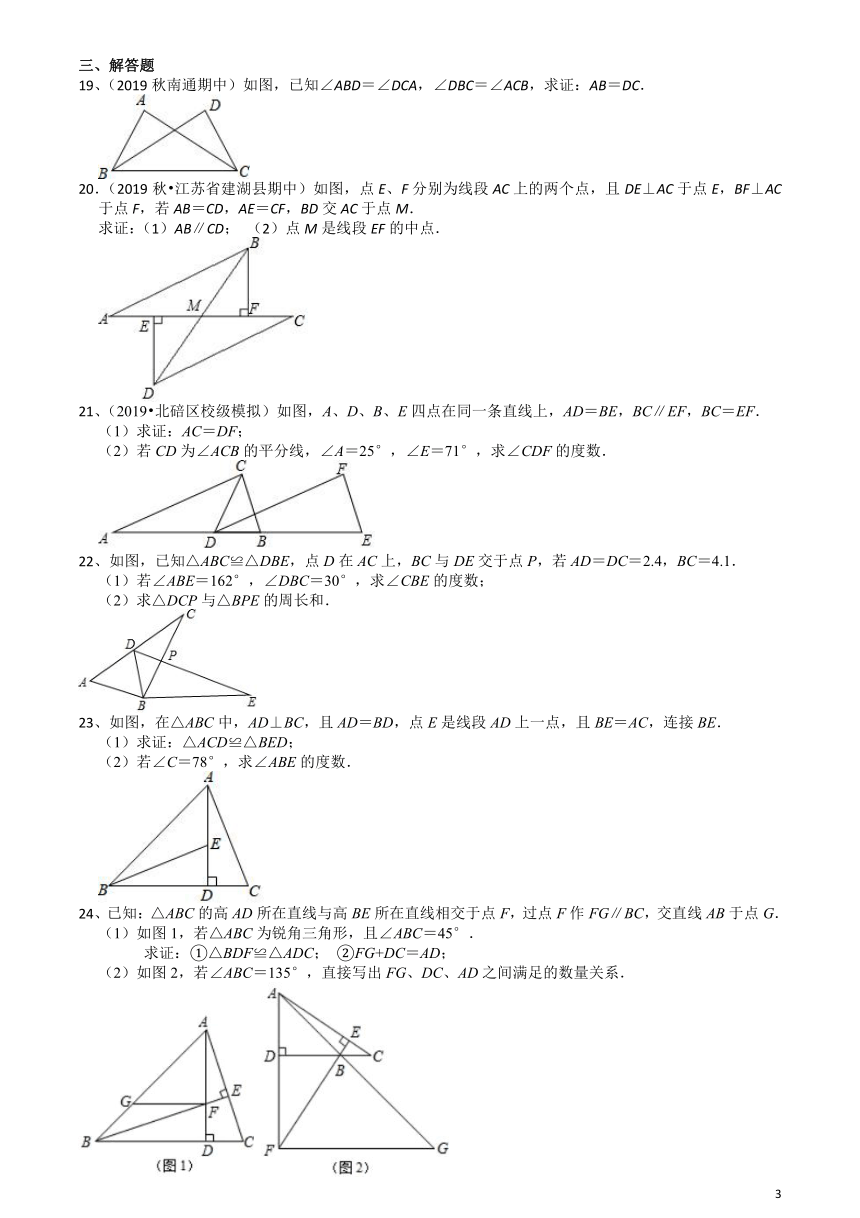
19、(2019秋南通期中)如图,已知∠ABD=∠DCA,∠DBC=∠ACB,求证:AB=DC.
20.(2019秋?江苏省建湖县期中)如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
求证:(1)AB∥CD;
(2)点M是线段EF的中点.
21、(2019?北碚区校级模拟)如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.
(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
22、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
23、如图,在△ABC中,AD⊥BC,且AD=BD,点E是线段AD上一点,且BE=AC,连接BE.
(1)求证:△ACD≌△BED;
(2)若∠C=78°,求∠ABE的度数.
24、已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
25、阅读下面材料:
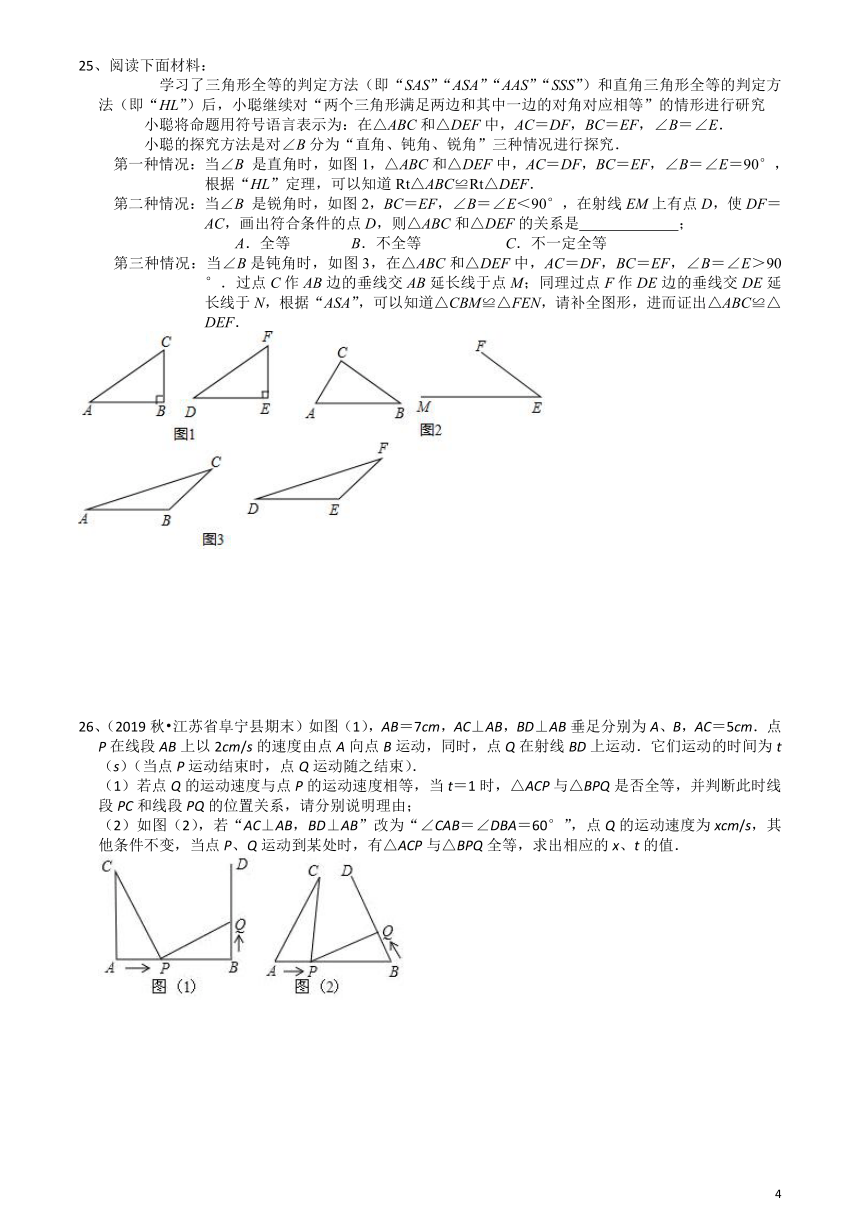
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B
是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B
是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是
;
?A.全等
B.不全等
C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.
26、(2019秋?江苏省阜宁县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
苏科版2020-2021八年级数学上册1章全等三角形章末复习训练卷(有答案)
一、选择题
1、下列四个图形中,属于全等图形的是( D )
A.③和④
B.②和③
C.①和③
D.①②
2、下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
解:A、如果两个图形全等,那么它们的形状和大小一定相同,正确,不合题意;
B、面积相等的两个图形是全等图形,错误,符合题意;
C、图形全等,只与形状、大小有关,而与它们的位置无关,正确,不合题意;
D、全等三角形的对应边相等,对应角相等,正确,不合题意;
故选:B.
3、如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.
B.
C.
D.
解:在△ABC中,∠B=180°﹣58°﹣72°=50°,
根据“SAS”可判断图甲的三角形与△ABC全等.
故选:A.
4、如图,∠ADC=∠ADB,添加一个条件,仍不能说明△ABD≌△ACD的是( )
A.AB=AC
B.∠BAD=∠CAD
C.∠B=∠C
D.BD=CD
解:A、添加AB=AC,利用SSA不能判定△ABD≌△ACD,故此选项符合题意;
B、添加∠BAD=∠CAD,利用ASA能判定△ABD≌△ACD,故此选项不合题意;
C、添加∠B=∠C,利用AAS能判定△ABD≌△ACD,故此选项不合题意;
D、添加BD=CD,可利用SAS能判定△ABD≌△ACD,故此选项不合题意;
故选:A.
5、如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,
故选:C.
6、如图,已知AB=DE,∠B=∠E,添加下列哪个条件可以利用SAS判断△ABC≌△DEC.正确的是: ② .
①∠A=∠D;②BC=EC;③AC=DC;④∠BCE=∠ACD.
【解答】解:∵AB=DE,∠B=∠E,
∴添加①∠A=∠D,利用ASA得出△ABC≌△DEC;
∴添加②BC=EC,利用SAS得出△ABC≌△DEC;
∴添加④∠BCE=∠ACD,得出∠ACB=∠DCE,利用AAS得出△ABC≌△DEC;
故答案为:②.
7、如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5
B.6
C.7
解:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,∠BAC=∠DCA,
在△ABD和△CDB中,,
∴△ABD≌△CDB(ASA),
同理:△ABC≌△CDA(ASA);
∴AB=CD,BC=DA,
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS);
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS);
图中共有7对全等三角形;
故选:C.
8、(2019秋江都区期中)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC?BD,其中正确的结论有(C )
A.0个
B.1个
C.2个
D.3个
【分析】先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.
【解析】在△ABD与△CBD中,,∴△ABD≌△CBD(SSS),故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,,∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故②正确;
四边形ABCD的面积=S△ABD+S△BDCAC?BD,故③错误;
故选:C.
9、(2019秋?江苏省仪征市校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( B )
A.105°
B.100°
C.110°
D.115°
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
【解析】延长C′D交AB′于H.
∵△AEB≌△AEB′,∴∠ABE=∠AB′E,
∵C′H∥EB′,∴∠AHC′=∠AB′E,∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,∴∠C′AH=120°,∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.
二、填空题
10、如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
解:∵图中的两个三角形全等,∴∠α=68°.故答案为68.
11、如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
解:∵Rt△ABC和Rt△EDF中,∴∠BAC=∠DEF=90°,
∵BC∥DF,∴∠DFE=∠BCA,∴添加AB=ED,
在Rt△ABC和Rt△EDF中,∴Rt△ABC≌Rt△EDF(AAS),
故答案为:AB=ED答案不唯一.
12、如图,AB与CD交于点O,,,,,则的度数为______
.
解:在和中,≌,,
13、如图,在3×3的正方形网格中,∠1+∠2=
度.
解:如右图所示,∵AB=BE,BC=BD,∠ABC=∠EBD=90°,∴△ABC≌△EBD(SAS),
∴∠ACB=∠1,
∵∠ACB+∠2=90°,∴∠1+∠2=90°,故答案为:90.
14、如图,等腰△ABC,CA=CB,△A′BC′≌△ABC,∠A′=75°,∠A′BA=β,
则∠ACC′的度数为
.(用含β的式子表示)
解:∵△A′BC′≌△ABC,∴∠A=∠A′=75°,BC′=BC,∠A′BC′=∠ABC,
∴∠C′BC=∠A′BA=β,
∵BC′=BC,∴∠BCC′=,
∵CA=CB,∴∠ACB=180°﹣75°×2=30°,
∴∠ACC′=∠BCC′﹣∠ACB=60°﹣β,
故答案为:60°﹣β.
15、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,
连结BF,CE.下列说法:①△ABD和△ACD面积相等;
②∠BAD=∠CAD;③△BDF≌△CDE;
④BF∥CE;⑤CE=AE.其中正确的有
.(把你认为正确的序号都填上)
解:∵BD=CD,点A到BD、CD的距离相等,∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,∴△BDF≌△CDE,故③正确;
∴∠F=∠DEC,∴BF∥CE,故④正确;
∵△BDF≌△CDE,∴CE=BF,故⑤错误,
故答案为:①③④.
16、(2019秋?江苏省建湖县期中)如图所示,AD=AE,AB=AC,∠BAC=∠DAE,B、D、E在同一直线上,∠1=22°,∠2=30°,则∠3= 52° .
【分析】由“SAS”可证△ABD≌△ACE,可得∠ABD=∠2=30°,由三角形外角性质可求解.
【解析】∵∠BAC=∠DAE,
∴∠1=∠CAE,且AD=AE,AB=AC,
∴△ABD≌△ACE(SAS)
∴∠ABD=∠2=30°,
∴∠3=∠2+∠ABD=52°,
故答案为:52°
17、(2019秋?江苏桦南期中)如图,∠DAB=∠EAC=65°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是 115° .
【分析】首先得出∠DAC=∠EAB,进而利用ASA得出△ADC≌△AEB,进而得出∠E=∠ACD,再利用三角形内角和定理得出∠EAF=∠COF=65°,即可得出答案.
【解析】∵∠DAB=∠EAC=65°,∴∠DAB+∠BAC=∠BAC+∠EAC,∴∠DAC=∠EAB,
在△ADC和△AEB中,,∴△ADC≌△AEB(SAS),∴∠E=∠ACD,
又∵∠AFE=∠OFC,∴∠EAF=∠COF=65°,∴∠DOE=180°﹣∠COF=115°.
故答案为:115°.
18、(2020春?文登区期中)已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足,下列结论:①;②;
③;④,其中正确的结论有 ①②④ (填序号).
【解答】解:①为的角平分线,,
在和中,,,①正确;
②为的角平分线,,,,
,,,②正确;
③,,,,
,为等腰三角形,,
,,,
为的角平分线,,而不垂直与,,③错误;
④过作于点,
是上的点,,
在和中,,,,
在和中,,,,
,④正确.
故答案为:①②④.
三、解答题
19、(2019秋南通期中)如图,已知∠ABD=∠DCA,∠DBC=∠ACB,求证:AB=DC.
【解答】证明:∵∠ABD=∠DCA,∠DBC=∠ACB,∴∠ABD+∠DBC=∠DCA+∠ACB
即∠ABC=∠DCB
在△ABC和△DCB中
,∴△ABC≌△DCB(ASA),∴AB=DC
20.(2019秋?江苏省建湖县期中)如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
求证:(1)AB∥CD;
(2)点M是线段EF的中点.
【解答】证明:(1)∵AE=CF,∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL),∴∠BAF=∠DCE,∴AB∥CD;
(2)∵Rt△ABF≌Rt△CDE,∴DE=BF,
在△DEM和△BFM中,,∴△DEM≌△BFM(AAS),∴MB=MD.
即点M是线段EF的中点.
21、(2019?北碚区校级模拟)如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.
(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
【解答】证明:(1)∵AD=BE,∴AB=DE
∵BC∥EF,∴∠ABC=∠DEF,且AB=BE,BC=EF,∴△ABC≌△DEF(SAS),∴AC=DF
(2)∵△ABC≌△DEF,∴∠ABC=∠E=71°,∠A=∠FDE=25°
∴∠ACB=180°﹣∠A﹣∠ABC=84°
∵CD为∠ACB的平分线,∴∠ACD=42°=∠BCD
∵∠CDB=∠A+∠ACD=∠CDF+∠EDF,∴∠CDF=42°
22、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,∴∠ABC=∠DBE,∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+BP+BP+PE+BE=DC+DE+BC+BE=15.4.
23、如图,在△ABC中,AD⊥BC,且AD=BD,点E是线段AD上一点,且BE=AC,连接BE.
(1)求证:△ACD≌△BED;
(2)若∠C=78°,求∠ABE的度数.
【解答】(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,∴∠CAD+∠C=90°,
∵AD=BD,BE=AC,∴Rt△BDE≌Rt△ADC(HL);
(2)解:∵△ACD≌△BED,∴∠DAC=∠DBE,
∵∠CAD+∠C=90°,∴∠DBE=∠CAD=90°﹣78=12°,
∵AD=BD,AD⊥BC,∴△ABD是等腰直角三角形,∴∠ABD=45°,
∴∠ABE=∠ABD﹣∠DBE=45°﹣12°=33°.
24、已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
解:(1)①证明:∵∠ADB=90°,∠ABC=45°,∴∠BAD=∠ABC=45°,∴AD=BD;
∵∠BEC=90°,∴∠CBE+∠C=90°,又∵∠DAC+∠C=90°,∴∠CBE=∠DAC;
∵∠FDB=∠CDA=90°,∴△FDB≌△CDA(ASA)
②∵△FDB≌△CDA,∴DF=DC;
∵GF∥BC,∴∠AGF=∠ABC=45°,∴∠AGF=∠BAD,∴FA=FG;∴FG+DC=FA+DF=AD.
(2)FG、DC、AD之间的数量关系为:FG=DC+AD.
理由:∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,
∴BD=AD,FG=AF=AD+DF;
∵∠FAE+∠DFB=∠FAE+∠DCA=90°,∴∠DFB=∠DCA;
又∵∠FDB=∠CDA=90°,BD=AD,∴△BDF≌△ADC(AAS);
∴DF=DC,∴FG、DC、AD之间的数量关系为:FG=DC+AD.
25、阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B
是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B
是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是
;
?A.全等
B.不全等
C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.
解:第二种情况选C.
理由:由题意满足条件的点D有两个,故△ABC和△DEF不一定全等(如图所示)
故选C.
第三种情况补全图.
证明:由△CBM≌△FEN得,CM=FN,BD=EN
又在Rt△CMA和Rt△FND中,∴△CMA≌△FND,∴AM=DN,∴AB=DE,
又在△ABC和△DEF中,∴△ABC≌△DEF.
26、(2019秋?江苏省阜宁县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
【分析】(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
【解析】(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB∴∠A=∠B=90°
∵AP=BQ=2,∴BP=5,∴BP=AC,
在△ACP和△BPQ中,,∴△ACP≌△BPQ;∴∠C=∠BPQ,
∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,∴∠CPQ=90°,∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt解得:x=2,t=1;
②若△ACP≌△BQP,则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t,解得:x,t.
一、选择题
1、下列四个图形中,属于全等图形的是( )
A.③和④
B.②和③
C.①和③
D.①②
2、下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
3、如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.
B.
C.
D.
4、如图,∠ADC=∠ADB,添加一个条件,仍不能说明△ABD≌△ACD的是( )
A.AB=AC
B.∠BAD=∠CAD
C.∠B=∠C
D.BD=CD
(4题)
(5题)
5、如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
6、如图,已知AB=DE,∠B=∠E,添加下列哪个条件可以利用SAS判断△ABC≌△DEC.正确的是: .
①∠A=∠D;②BC=EC;③AC=DC;④∠BCE=∠ACD.
(6题)
(7题)
7、如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5
B.6
C.7
8、(2019秋江都区期中)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC?BD,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
9、(2019秋?江苏省仪征市校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A.105°
B.100°
C.110°
D.115°
二、填空题
10、如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
(10题)
(11题)
(12题)
11、如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
12、如图,AB与CD交于点O,,,,,则的度数为______
13、如图,在3×3的正方形网格中,∠1+∠2=
度.
(13题)
(14题)
(15题)
14、如图,等腰△ABC,CA=CB,△A′BC′≌△ABC,∠A′=75°,∠A′BA=β,
则∠ACC′的度数为
.(用含β的式子表示)
15、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,
连结BF,CE.下列说法:①△ABD和△ACD面积相等;
②∠BAD=∠CAD;③△BDF≌△CDE;
④BF∥CE;⑤CE=AE.其中正确的有
.(把你认为正确的序号都填上)
16、(2019秋?江苏省建湖县期中)如图所示,AD=AE,AB=AC,∠BAC=∠DAE,B、D、E在同一直线上,∠1=22°,∠2=30°,则∠3=
.
(16题)
(17题)
(18题)
17、(2019秋?江苏桦南期中)如图,∠DAB=∠EAC=65°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是
.
18、(2020春?文登区期中)已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足,下列结论:①;②;
③;④,其中正确的结论有
(填序号).
三、解答题
19、(2019秋南通期中)如图,已知∠ABD=∠DCA,∠DBC=∠ACB,求证:AB=DC.
20.(2019秋?江苏省建湖县期中)如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
求证:(1)AB∥CD;
(2)点M是线段EF的中点.
21、(2019?北碚区校级模拟)如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.
(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
22、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
23、如图,在△ABC中,AD⊥BC,且AD=BD,点E是线段AD上一点,且BE=AC,连接BE.
(1)求证:△ACD≌△BED;
(2)若∠C=78°,求∠ABE的度数.
24、已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
25、阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B
是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B
是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是
;
?A.全等
B.不全等
C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.
26、(2019秋?江苏省阜宁县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
苏科版2020-2021八年级数学上册1章全等三角形章末复习训练卷(有答案)
一、选择题
1、下列四个图形中,属于全等图形的是( D )
A.③和④
B.②和③
C.①和③
D.①②
2、下列说法不正确的是( )
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.全等三角形的对应边相等,对应角相等
解:A、如果两个图形全等,那么它们的形状和大小一定相同,正确,不合题意;
B、面积相等的两个图形是全等图形,错误,符合题意;
C、图形全等,只与形状、大小有关,而与它们的位置无关,正确,不合题意;
D、全等三角形的对应边相等,对应角相等,正确,不合题意;
故选:B.
3、如图,已知△ABC,下面甲、乙、丙、丁四个三角形中,与△ABC全等的是( )
A.
B.
C.
D.
解:在△ABC中,∠B=180°﹣58°﹣72°=50°,
根据“SAS”可判断图甲的三角形与△ABC全等.
故选:A.
4、如图,∠ADC=∠ADB,添加一个条件,仍不能说明△ABD≌△ACD的是( )
A.AB=AC
B.∠BAD=∠CAD
C.∠B=∠C
D.BD=CD
解:A、添加AB=AC,利用SSA不能判定△ABD≌△ACD,故此选项符合题意;
B、添加∠BAD=∠CAD,利用ASA能判定△ABD≌△ACD,故此选项不合题意;
C、添加∠B=∠C,利用AAS能判定△ABD≌△ACD,故此选项不合题意;
D、添加BD=CD,可利用SAS能判定△ABD≌△ACD,故此选项不合题意;
故选:A.
5、如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个
B.2个
C.3个
D.4个
解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,
故选:C.
6、如图,已知AB=DE,∠B=∠E,添加下列哪个条件可以利用SAS判断△ABC≌△DEC.正确的是: ② .
①∠A=∠D;②BC=EC;③AC=DC;④∠BCE=∠ACD.
【解答】解:∵AB=DE,∠B=∠E,
∴添加①∠A=∠D,利用ASA得出△ABC≌△DEC;
∴添加②BC=EC,利用SAS得出△ABC≌△DEC;
∴添加④∠BCE=∠ACD,得出∠ACB=∠DCE,利用AAS得出△ABC≌△DEC;
故答案为:②.
7、如图,AB∥CD,AD∥BC,AC与BD相交于点O,AE⊥BD,CF⊥AC,垂足分别是E,F.则图中共有( )对全等三角形.
A.5
B.6
C.7
解:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,∠BAC=∠DCA,
在△ABD和△CDB中,,
∴△ABD≌△CDB(ASA),
同理:△ABC≌△CDA(ASA);
∴AB=CD,BC=DA,
在△AOB和△COD中,,
∴△AOB≌△COD(AAS),
同理:△AOD≌△COB(AAS);
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AEO=∠CFD=∠CFO=90°,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
同理:△AOE≌△COF(AAS),△ADE≌△CBF(AAS);
图中共有7对全等三角形;
故选:C.
8、(2019秋江都区期中)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC?BD,其中正确的结论有(C )
A.0个
B.1个
C.2个
D.3个
【分析】先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.
【解析】在△ABD与△CBD中,,∴△ABD≌△CBD(SSS),故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,,∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故②正确;
四边形ABCD的面积=S△ABD+S△BDCAC?BD,故③错误;
故选:C.
9、(2019秋?江苏省仪征市校级期中)如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( B )
A.105°
B.100°
C.110°
D.115°
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
【解析】延长C′D交AB′于H.
∵△AEB≌△AEB′,∴∠ABE=∠AB′E,
∵C′H∥EB′,∴∠AHC′=∠AB′E,∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,∴∠C′AH=120°,∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.
二、填空题
10、如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
解:∵图中的两个三角形全等,∴∠α=68°.故答案为68.
11、如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件
,使Rt△ABC和Rt△EDF全等.
解:∵Rt△ABC和Rt△EDF中,∴∠BAC=∠DEF=90°,
∵BC∥DF,∴∠DFE=∠BCA,∴添加AB=ED,
在Rt△ABC和Rt△EDF中,∴Rt△ABC≌Rt△EDF(AAS),
故答案为:AB=ED答案不唯一.
12、如图,AB与CD交于点O,,,,,则的度数为______
.
解:在和中,≌,,
13、如图,在3×3的正方形网格中,∠1+∠2=
度.
解:如右图所示,∵AB=BE,BC=BD,∠ABC=∠EBD=90°,∴△ABC≌△EBD(SAS),
∴∠ACB=∠1,
∵∠ACB+∠2=90°,∴∠1+∠2=90°,故答案为:90.
14、如图,等腰△ABC,CA=CB,△A′BC′≌△ABC,∠A′=75°,∠A′BA=β,
则∠ACC′的度数为
.(用含β的式子表示)
解:∵△A′BC′≌△ABC,∴∠A=∠A′=75°,BC′=BC,∠A′BC′=∠ABC,
∴∠C′BC=∠A′BA=β,
∵BC′=BC,∴∠BCC′=,
∵CA=CB,∴∠ACB=180°﹣75°×2=30°,
∴∠ACC′=∠BCC′﹣∠ACB=60°﹣β,
故答案为:60°﹣β.
15、如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,
连结BF,CE.下列说法:①△ABD和△ACD面积相等;
②∠BAD=∠CAD;③△BDF≌△CDE;
④BF∥CE;⑤CE=AE.其中正确的有
.(把你认为正确的序号都填上)
解:∵BD=CD,点A到BD、CD的距离相等,∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,∴△BDF≌△CDE,故③正确;
∴∠F=∠DEC,∴BF∥CE,故④正确;
∵△BDF≌△CDE,∴CE=BF,故⑤错误,
故答案为:①③④.
16、(2019秋?江苏省建湖县期中)如图所示,AD=AE,AB=AC,∠BAC=∠DAE,B、D、E在同一直线上,∠1=22°,∠2=30°,则∠3= 52° .
【分析】由“SAS”可证△ABD≌△ACE,可得∠ABD=∠2=30°,由三角形外角性质可求解.
【解析】∵∠BAC=∠DAE,
∴∠1=∠CAE,且AD=AE,AB=AC,
∴△ABD≌△ACE(SAS)
∴∠ABD=∠2=30°,
∴∠3=∠2+∠ABD=52°,
故答案为:52°
17、(2019秋?江苏桦南期中)如图,∠DAB=∠EAC=65°,AB=AD,AC=AE,BE和CD相交于点O,AB和CD相交于P,AC和BE相交于F,则∠DOE的度数是 115° .
【分析】首先得出∠DAC=∠EAB,进而利用ASA得出△ADC≌△AEB,进而得出∠E=∠ACD,再利用三角形内角和定理得出∠EAF=∠COF=65°,即可得出答案.
【解析】∵∠DAB=∠EAC=65°,∴∠DAB+∠BAC=∠BAC+∠EAC,∴∠DAC=∠EAB,
在△ADC和△AEB中,,∴△ADC≌△AEB(SAS),∴∠E=∠ACD,
又∵∠AFE=∠OFC,∴∠EAF=∠COF=65°,∴∠DOE=180°﹣∠COF=115°.
故答案为:115°.
18、(2020春?文登区期中)已知:如图,为的角平分线,且,为延长线上的一点,,过作,为垂足,下列结论:①;②;
③;④,其中正确的结论有 ①②④ (填序号).
【解答】解:①为的角平分线,,
在和中,,,①正确;
②为的角平分线,,,,
,,,②正确;
③,,,,
,为等腰三角形,,
,,,
为的角平分线,,而不垂直与,,③错误;
④过作于点,
是上的点,,
在和中,,,,
在和中,,,,
,④正确.
故答案为:①②④.
三、解答题
19、(2019秋南通期中)如图,已知∠ABD=∠DCA,∠DBC=∠ACB,求证:AB=DC.
【解答】证明:∵∠ABD=∠DCA,∠DBC=∠ACB,∴∠ABD+∠DBC=∠DCA+∠ACB
即∠ABC=∠DCB
在△ABC和△DCB中
,∴△ABC≌△DCB(ASA),∴AB=DC
20.(2019秋?江苏省建湖县期中)如图,点E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
求证:(1)AB∥CD;
(2)点M是线段EF的中点.
【解答】证明:(1)∵AE=CF,∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL),∴∠BAF=∠DCE,∴AB∥CD;
(2)∵Rt△ABF≌Rt△CDE,∴DE=BF,
在△DEM和△BFM中,,∴△DEM≌△BFM(AAS),∴MB=MD.
即点M是线段EF的中点.
21、(2019?北碚区校级模拟)如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.
(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
【解答】证明:(1)∵AD=BE,∴AB=DE
∵BC∥EF,∴∠ABC=∠DEF,且AB=BE,BC=EF,∴△ABC≌△DEF(SAS),∴AC=DF
(2)∵△ABC≌△DEF,∴∠ABC=∠E=71°,∠A=∠FDE=25°
∴∠ACB=180°﹣∠A﹣∠ABC=84°
∵CD为∠ACB的平分线,∴∠ACD=42°=∠BCD
∵∠CDB=∠A+∠ACD=∠CDF+∠EDF,∴∠CDF=42°
22、如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,∴∠ABC=∠DBE,∴∠ABD=∠CBE=132°÷2=66°,即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+BP+BP+PE+BE=DC+DE+BC+BE=15.4.
23、如图,在△ABC中,AD⊥BC,且AD=BD,点E是线段AD上一点,且BE=AC,连接BE.
(1)求证:△ACD≌△BED;
(2)若∠C=78°,求∠ABE的度数.
【解答】(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,∴∠CAD+∠C=90°,
∵AD=BD,BE=AC,∴Rt△BDE≌Rt△ADC(HL);
(2)解:∵△ACD≌△BED,∴∠DAC=∠DBE,
∵∠CAD+∠C=90°,∴∠DBE=∠CAD=90°﹣78=12°,
∵AD=BD,AD⊥BC,∴△ABD是等腰直角三角形,∴∠ABD=45°,
∴∠ABE=∠ABD﹣∠DBE=45°﹣12°=33°.
24、已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;
②FG+DC=AD;
(2)如图2,若∠ABC=135°,直接写出FG、DC、AD之间满足的数量关系.
解:(1)①证明:∵∠ADB=90°,∠ABC=45°,∴∠BAD=∠ABC=45°,∴AD=BD;
∵∠BEC=90°,∴∠CBE+∠C=90°,又∵∠DAC+∠C=90°,∴∠CBE=∠DAC;
∵∠FDB=∠CDA=90°,∴△FDB≌△CDA(ASA)
②∵△FDB≌△CDA,∴DF=DC;
∵GF∥BC,∴∠AGF=∠ABC=45°,∴∠AGF=∠BAD,∴FA=FG;∴FG+DC=FA+DF=AD.
(2)FG、DC、AD之间的数量关系为:FG=DC+AD.
理由:∵∠ABC=135°,∴∠ABD=45°,△ABD、△AGF皆为等腰直角三角形,
∴BD=AD,FG=AF=AD+DF;
∵∠FAE+∠DFB=∠FAE+∠DCA=90°,∴∠DFB=∠DCA;
又∵∠FDB=∠CDA=90°,BD=AD,∴△BDF≌△ADC(AAS);
∴DF=DC,∴FG、DC、AD之间的数量关系为:FG=DC+AD.
25、阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B
是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B
是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是
;
?A.全等
B.不全等
C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.
解:第二种情况选C.
理由:由题意满足条件的点D有两个,故△ABC和△DEF不一定全等(如图所示)
故选C.
第三种情况补全图.
证明:由△CBM≌△FEN得,CM=FN,BD=EN
又在Rt△CMA和Rt△FND中,∴△CMA≌△FND,∴AM=DN,∴AB=DE,
又在△ABC和△DEF中,∴△ABC≌△DEF.
26、(2019秋?江苏省阜宁县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.
【分析】(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
【解析】(1)△ACP≌△BPQ,
∵AC⊥AB,BD⊥AB∴∠A=∠B=90°
∵AP=BQ=2,∴BP=5,∴BP=AC,
在△ACP和△BPQ中,,∴△ACP≌△BPQ;∴∠C=∠BPQ,
∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,∴∠CPQ=90°,∴PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt解得:x=2,t=1;
②若△ACP≌△BQP,则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t,解得:x,t.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
