北师大版八年级数学上册课件:2.1认识无理数(共28张PPT)
文档属性
| 名称 | 北师大版八年级数学上册课件:2.1认识无理数(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 497.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 19:33:47 | ||
图片预览








文档简介
(共28张PPT)
2.1认识无理数
温故互查:(二人小组完成)
1、有理数的分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
温故互查:(二人小组完成)
2、小数的分类
小数
有限小数
无限小数
无限循环小数
无限不循环小数
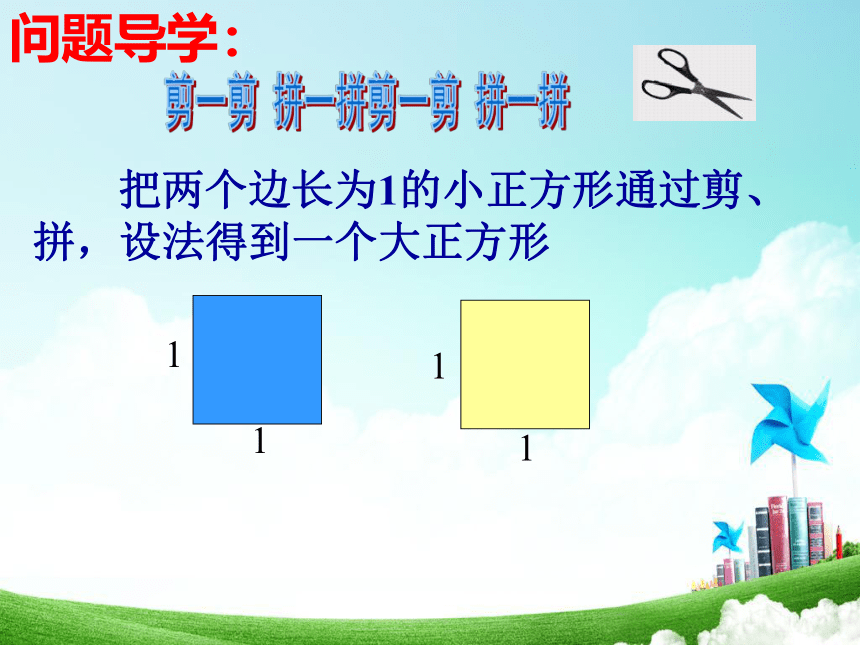
问题导学:
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
剪一剪
拼一拼
1
1
1
1
问题导学:
1
1
变化的世界
奇妙的组合
拼图:
问题导学:
因为正方形的面积为2
所以
(1)设大正方形的边长为a,a满足什么条件?
问题导学:
越来越大,
所以a不可能是整数
a可能是整数吗?
问题导学:
a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
问题导学:
a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
问题导学:
a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
问题导学:
a既不是整数又不是分数,所以a一定不是
。
那么a到底是什么数呢?
有理数
古人把这个数取名为无理数。
问题导学:
2
1
1、如图,以直角三角形的斜边为边的正方形的面积是多少?
在直角三角形中,由勾股定理得,
斜边?=1?+2?=5,所以直角三角形的斜边为边的正方形的面积是5.
2、设该正方形的边长为b,b满足什么条件?
b?=5
3、b是有理数吗?说说你的理由。
b不是有理数。
在上面两个问题中,
a,b是确实存在
的数,但都不是有理数。
问题导学:
1、大家判断一下3个正方形的边长之间有怎样的大小关系?说说你的理由.
2、大家能不能判断一下面积为2的正方形的边长a的大致范围呢?
问题导学:
边长a
面积S
1<a<2
1<S<4
1.4<a<1.5
1.96<S<2.25
1.41<a<1.42
1.9881<S<2.0164
1.414<a<1.415
1.999396<S<2.002225
1.4142<a<1.4143
1.99996164<S<2.00024449
问题导学:
无理数的定义,请大家把下列各数表示成小数.
并看它们是有限小数还是无限小数,是循环小数还是不循环小数?
问题导学:
像上面研究过的a2=2,b2=5中的a,b是无限不循环小数.无限不循环小数叫无理数
除上面的a,b外,圆周率π=3.14159265…也是一个无限不循环小数,0.5858858885…(相邻两个5之间8的个数逐次加1)也是一个无限不循环小数,它们都是无理数.
自学检测:
1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
自学检测:
如图,每个小正方形的边长为1,四边形ABCD的对角线AC,BD相交于O。试说明边长AB,BC,CD,AD和对角线AC,BD的长度哪些是有理数,哪些不是有理数?
典型例题:
生活中真的有很多不是有理数的数吗?
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
典型例题:
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
巩固练习:
1、长和宽分别是3,2的长方形,它的对角线的长可能是整数吗?可能是分数吗?
巩固练习:
2、请你在如图所示的方格纸上按照如下要求设计直角三角形:
(1)使它的三边中有一边边长不是有理数。
(2)使它的三边中有两边边长不是有理数。
(3)使它的三边边长不是有理数。
巩固练习:
巩固练习:
巩固练习:
谈谈你这节课的收获吧!
课堂小结:
作业:
习题:4.2
1、2
再见
2.1认识无理数
温故互查:(二人小组完成)
1、有理数的分类:
有理数
整数
分数
正整数
负整数
0
正分数
负分数
温故互查:(二人小组完成)
2、小数的分类
小数
有限小数
无限小数
无限循环小数
无限不循环小数
问题导学:
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
剪一剪
拼一拼
1
1
1
1
问题导学:
1
1
变化的世界
奇妙的组合
拼图:
问题导学:
因为正方形的面积为2
所以
(1)设大正方形的边长为a,a满足什么条件?
问题导学:
越来越大,
所以a不可能是整数
a可能是整数吗?
问题导学:
a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
问题导学:
a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
问题导学:
a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
问题导学:
a既不是整数又不是分数,所以a一定不是
。
那么a到底是什么数呢?
有理数
古人把这个数取名为无理数。
问题导学:
2
1
1、如图,以直角三角形的斜边为边的正方形的面积是多少?
在直角三角形中,由勾股定理得,
斜边?=1?+2?=5,所以直角三角形的斜边为边的正方形的面积是5.
2、设该正方形的边长为b,b满足什么条件?
b?=5
3、b是有理数吗?说说你的理由。
b不是有理数。
在上面两个问题中,
a,b是确实存在
的数,但都不是有理数。
问题导学:
1、大家判断一下3个正方形的边长之间有怎样的大小关系?说说你的理由.
2、大家能不能判断一下面积为2的正方形的边长a的大致范围呢?
问题导学:
边长a
面积S
1<a<2
1<S<4
1.4<a<1.5
1.96<S<2.25
1.41<a<1.42
1.9881<S<2.0164
1.414<a<1.415
1.999396<S<2.002225
1.4142<a<1.4143
1.99996164<S<2.00024449
问题导学:
无理数的定义,请大家把下列各数表示成小数.
并看它们是有限小数还是无限小数,是循环小数还是不循环小数?
问题导学:
像上面研究过的a2=2,b2=5中的a,b是无限不循环小数.无限不循环小数叫无理数
除上面的a,b外,圆周率π=3.14159265…也是一个无限不循环小数,0.5858858885…(相邻两个5之间8的个数逐次加1)也是一个无限不循环小数,它们都是无理数.
自学检测:
1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
自学检测:
如图,每个小正方形的边长为1,四边形ABCD的对角线AC,BD相交于O。试说明边长AB,BC,CD,AD和对角线AC,BD的长度哪些是有理数,哪些不是有理数?
典型例题:
生活中真的有很多不是有理数的数吗?
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出两条长度是有理数的线段和两条长度不是有理数的线段。
典型例题:
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
巩固练习:
1、长和宽分别是3,2的长方形,它的对角线的长可能是整数吗?可能是分数吗?
巩固练习:
2、请你在如图所示的方格纸上按照如下要求设计直角三角形:
(1)使它的三边中有一边边长不是有理数。
(2)使它的三边中有两边边长不是有理数。
(3)使它的三边边长不是有理数。
巩固练习:
巩固练习:
巩固练习:
谈谈你这节课的收获吧!
课堂小结:
作业:
习题:4.2
1、2
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
