华东师大版九年级数学上册第21章二次根式全章课件(共99张PPT)
文档属性
| 名称 | 华东师大版九年级数学上册第21章二次根式全章课件(共99张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 14:48:36 | ||
图片预览










文档简介
(共99张PPT)
1.二次根式
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
⑵什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根。
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根。
0的算术平方根平方根是0.
温故知新
a的平方根是±
a
用
(a≥0)表示。
a
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根。
(3)平方根的性质:
1、16的平方根是什么?
算术平方根是什么?
2、0的平方根是什么?算术平方根是什么?
3、-7有没有平方根?有没有算术平方根?
正数和0都有算术平方根;
负数没有算术平方根。
思考:
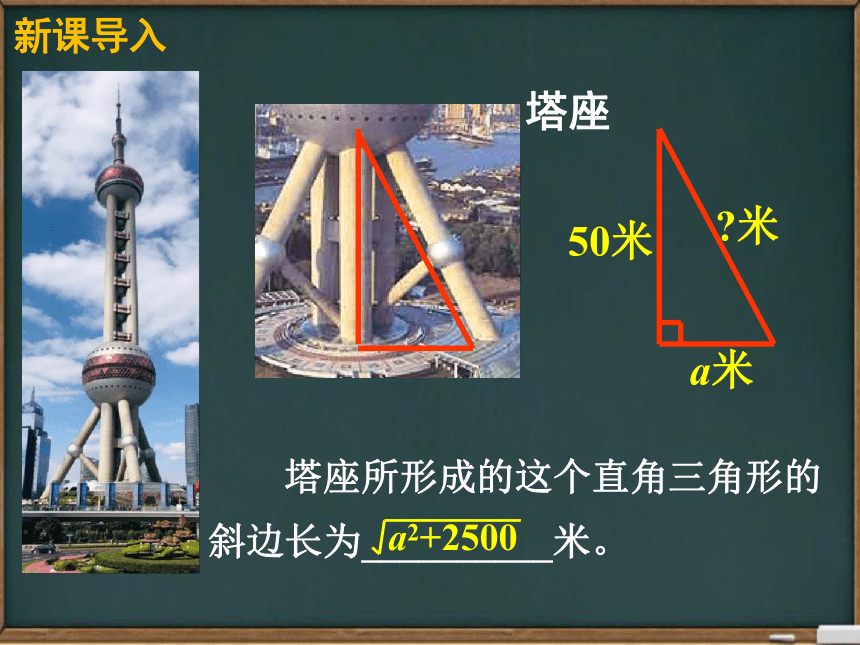
50米
a米
塔座所形成的这个直角三角形的
斜边长为__________米。
?米
塔座
a2+2500
新课导入
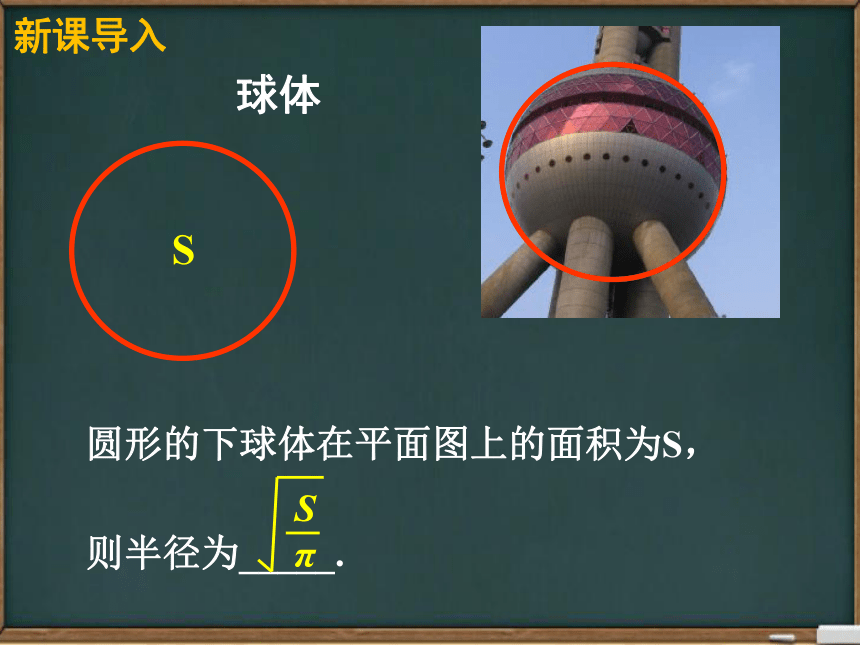
S
圆形的下球体在平面图上的面积为S,
则半径为_____.
球体
S
π
新课导入
如图所示的值表示正方形的面积,则
正方形的边长是
b-3
表示一些正数的算术平方根.
你认为所得的各代数式有哪些共同特点?
b-3
新课导入
a2+2500
S
π
b-3
归纳:
a2+2500
S
π
b-3
形如
(a≥0)的式子叫二次根式。
a
a叫被开方数.
请你凭着自己已有的知识,说说对二次根式的认识!
1、表示a的算术平方根;
形如
(a≥0)的式子叫二次根式。
a
理解:
2、a可以是数,也可以是式;
3、形式上含有二次根号
;
4、双重非负性:a≥0,
≥0;
a
5、既可表示开方运算,也可表示运算的结果.
1、下列各式是二次根式吗?
?
巩固认识
(1)
32
(2)
-12
(3)
16
(4)
-m
(m≤0)
(5)
xy
(x、y异号)
(6)
a2+1
?
?
(7)
3
5
在实数范围内,负数没有平方根.
(8)
a2+2a+2
?
?
(9)
(m-3)2
2、求下列二次根式中字母的取值范围:
求二次根式中字母的取值范围的基本依据:
①被开方数不小于零;
②分母中有字母时,要保证分母不为零。
(1)
a+1
(3)
(a-3)2
1
1-2a
(4)
(2)
-2x
1
x2
(5)
3
3、若
=0,则
=
。
a-2
+
2b-7
a+2b
4、已知a、b为实数,且满足a=
+1
则a+b的值为
。
1-2b
+
2b-1
5、2+
的最小值为
,此时x的值为
。
3-x
6、已知
与
互为相反数,
则a=
,b=
。
a-b+6
a+b-8
=2
新知探究二
(
2
)2
(
4
)2
=4
(
17
)2
=17
1
3
(
)2
1
3
=
(
0
)2
=0
2
是2的算术平方根,根据算术平方根的意义,
2
是一个平方等于2的非负数,因此:
(
2
)2=2
即:一个非负数的算数平方根的平方
等于非负数本身。
一般地,二次根式有如下性质:
归纳:
(1)
≥0
(a≥0);
a
(2)(
a
)2=
a
(a≥0).
(2)对于
理解:
(1)
(a≥0)
a
表示非负数a的算术平方根.
也就是说,
(a≥0)
a
是一个非负数,它的
平方等于a;
(
a
)2=
a
(a≥0)
利用这一公式
可计算,如:
(
3
2
)2=32×
(
2
)2=9×2=18
如果把该公式反过来就是:
a=(
a
)2
其意义是:可以把任意非负数写成平方的形式。
如:
2=(
2
)2
a-b=(
a-b
)2
(a≥b)
1、你能把下列各数写成某个数的平方或
平方的相反数吗?
(1)
3
(2)
0.5
(3)
-5
(4)
a-b
例题解析:
解:
(1)
3=
(
3
)2
(2)
0.5=
(
0.5
)2
(3)
-5=
-(
5
)2
25,16呢?
(4)
a-b=
(
a-b
)2
(a≥b)
-(
b-a
)2
(a≤b)
例题解析:
2、计算:(1)
(2)
(
8
5
)2
2
7
(-7
)2
解:
(1)
(
8
5
)2
=
82×(
5
)2
=64×5
=320
2
7
(-7
)2
(2)
2
7
×(
)2
=
(-7)2
=49×
2
7
=14
评析:本题直接应用二次根式的性质
求解。当底数是积时,先用积的乘方法则计算,再运用二次根式的性质。
(
a
)2=
a(a≥0)
新知探究三
22
=
2
0.12
=
0.1
2
3
(-
)2
=
2
3
02
=
0
一般地,根据算术平方根的意义,得
a2
=|
a
|
即:一个任意数的平方的算术平方根等于
它本身的绝对值。
比较
和
1、从运算顺序来看:
先开方,后平方;
a2
(
a
)2
(
a
)2
a2
先平方,后开方。
2、从取值范围来看:
(
a
)2中,
a≥0;
a2中,
a取任何实数。
3、从运算结果来看:
(
a
)2=
a
(a≥0)
a2
=|
a
|=
a
(a≥0)
-a
(a<0)
解:(1)∵a≥1,∴a-1≥0,
例题解析:
计算:(1)
(2)
(a-1)2
(a≥1)
(3.14-π)2
∴
(a-1)2
=
|a-1
|=a-1.
(2)∵3.14<π,∴3.14-π<0,
∴
(3.14-π)2
=
|3.14-π
|=π-3.14.
评析:在计算时,为确保计算的正确性,计算
形如
的二次根式时,先要写成
的形式,
再看底数a的符号,防止出现当a<0时,
这样的错误。
a2
a2
=|a|
a2
=a
1、化简下列各式:
巩固认识
(
3
2
)2
+
(1)
(
2
3
)2
(2)
(-5)2
+
(
5
)2
(3)
m2-16m+64
(m<8)
(4)
a2b2
(a<0,
b<0
)
2、实数p在数轴上的位置如图所示,
化简:
(1-p)2
+
(
2-
p
)2
-1
0
1
p
2
3、已知a、b、c为△ABC的三边长,
化简:
(a-b-c)2
+
(b-a+c)2
1.
二次根式的概念
2.二次根式的基本性质
3.
二次根式的重要性质
知识小结
形如
(a≥0)的式子叫二次根式.
a
(1)
≥0
(a≥0);
a
a2
=|
a
|=
a
(a≥0)
-a
(a<0)
(
a
)2=
a
4.
注意
和
的区别与联系.
a2
=
a
(2)(
a
)2=
a
(a≥0).
5.
注意灵活应用二次根式的性质.
课后练习
1、计算:(1)
(
8
)2
+
(
-
3
)2
(2)
-(
-
10
)2
-(
-
3
3
)2
(3)
(
2
5
)2
2
5
-
(-
5
)2
(4)
(
x
xy
)2
-
·
(-y)2
x6
2、若1<x<4,化简代数式:
(x-4)2
+
(x-1)2
3、设a、b、c为△ABC的三边,化简:
(a+b+c)2
+
(a-b-c)2
+
(c-b+a)2
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.1二次根式的乘除法
知识回顾
1、二次根式
(a≥0)是非负数,
.当a≥0时,
=
;
当a<0时,
=
.
a
a
-a
2、单项式与单项式相乘,将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
知识应用
1、已知a<0<b,且∣a∣>∣b∣,那么
的化简结果为
.
2、计算:(1)3x2·(-2xy2)=
;
(2)(5×103)·(-3×102)=
.
0
-6x3y2
-1.5×106
探索1
1、认真观察:
2、模仿计算:
4
7
28
28
28
6
5
30
30
30
12
12
12
12
3、根据上面的结果,直接用“>、<或=”填空:
=
=
=
=
=
=
4、归纳:
=
当a≥0,b≥0时,
即二次根式的乘法法则为:
两个二次根式相乘,将它们的被开方数相乘。
5、应用:
4
利用法则直接写出结果:
-15
-60
6、拓展:
二次根式的乘法公式法则可以推广到多个二次根式相乘的运算.
如:计算
6×15×10
30
探索2
将
反过来,就得到
积的算术平方根,等于积中各因式的算术平方根的积.
积的算术平方根的应用
化简二次根式
如:
模仿上面的方法,化简:
9
2
9
2
拓展应用
(2)将根号外的因式移到根号内:
拓展应用
※拓展应用
比一比,看谁更快!
一、计算:
二、化简:
(2)
3、已知a、b为正实数,下列等式中,
一定成立的是(
)
B
4、下面的解题方法、过程对吗?
5、比较下列各组数的大小:
而20<27,
<
小
结
本节课要掌握:
(a≥0,b≥0)
(a≥0,b≥0)
对于二次根式的乘法及积的算术平方根的化简要灵活运用
课后练习
认真完成导学案的“课后练习题案”.
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.2二次根式的乘除法
温故知新
1、二次根式的乘法法则:两个二次根式相乘,
将它们的被开方数相乘。
用字母表示为:
推广到多个二次根式相乘:
2、积的算术平方根,等于积中各因式的
算术平方根的积.
用字母表示为:
计算化简:
12
知识应用
1、观察:
2、模仿:
探索一
3、根据上面的结果,直接用“>、<或=”填空:
=
=
=
=
=
=
4、归纳:
当a≥0,b>0时,
即二次根式的除法法则为:
两个二次根式相除,将它们的被开方数相除,再取商的算术平方根。
5、应用:
1.利用法则直接写出结果:
2.计算并化简结果:
注意:此处可不用括号
商的算术平方根,等于被除数和除数的算术平方根的商.
将
(a≥0,b>0)反过来,得:
(a≥0,b>0)
探索二
商的算术平方根的应用:
化简二次根式
如:
模仿上面的方法,化简:
解:
拓展应用
比一比,看谁更快!
计算化简:
知识拓展
学了本节知识后,小莉对小明提出了一个问题:“你能运用二次根式的除法法则比较下面两个式子的大小吗?”
同学们,你能帮小明解决这个问题吗?
看看谁的方法更好、更多!
知识拓展
学了本节知识后,小莉对小明提出了一个问题:“你能运用二次根式的除法法则比较下面两个式子的大小吗?”
方法一:规律法
方法二:求差法
方法三:运用乘法法则
方法四:乘方法
本节课要掌握:
(a≥0,b>0)
(a≥0,b>0)
对于二次根式的除法及商的算术平方根的化简要灵活运用
1、
2、
知识小结
课后作业
一、填空题:
1、分母有理化:
2、已知三角形的面积为
cm2,一边长
为
cm,则该边上的高是_____cm.
二、计算化简:
(m>0,
n>0)
(a>0)
三、解答题:
1、先化简下面的式子:
,
然后选择一个合适的x值,
代入化简后的式子求值。
2、站在海拔高度h米的地方,看见的水平距
离是d米,它们之间近似地符合公式
.
某一登山者从海拔n米登上海拔2n米的山顶,
那么他看到的水平距离是原来的多少倍?
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.3二次根式的乘除法
.
1、当a≥0,b≥0时,
;
反之,
2、当a≥0,b>0时,
;反之,
3、二次根式的乘除法及积(商)的算术平方根在具体问题中灵活使用,结果要化简.
4、把分母中含有的根号去掉的过程叫分母有理化.通过分母有理化,可化简二次根式。
温故知新
一、下面的计算正确吗?若不正确请改正:
知识应用
(a<0,
b<0)
解:都错误,正确的应为:
(2)∵a<0,
b<0,
二、计算化简:
解:
二、计算化简:
解:
1、计算:
2、观察上面计算题的最后结果,可以发现这些式子中的二次根式两个特点:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或
因式.
探索
3、归纳:
同时满足下列两个条件的二次根式是最简二次根式:
(1)被开方数不含分母(即被开方数中因数是整数,因式是整式);
(2)被开方数不含能开得尽方的因数或因式(即被开方数的因数或因式的幂的指数都小于2)
下列各式中是最简二次根式的是(
)
D
及时反馈
下列各式中是最简二次根式的是(
)
D
≠
切记
及时反馈
应用:
1、把下面的二次根式化为最简二次根式:
解:
2、如图,在Rt△ABC中,∠C=90?,
AC=2.5cm,BC=6cm,求AB的长.
B
C
A
解:由题意得
拓展:
解:
解:
解:
小
结
本节课要掌握:
2、利用分母有理化对含分母的二次根式进行化简.
1、最简二次根式的两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.
课后作业
1、化简:
(x>0)
2、已知a为实数,化简
阅读下面的解答过程,请判断是否正确?若不正确,请写出正确的解答过程:
解:
3、已知一个矩形的长为
,宽
为
,与它面积相等的圆的
半径为多少?
4、利用分母有理化巧算:
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
3.二次根式的加减法
1、最简二次根式的被开方数要满足两个条件:(1)不含分母;(2)不含能开得尽方的因数或因式。
2、同类项:含有相同的字母,并且相同字母的指数分别相同的项叫同类项。
3、合并同类项:将同类项的系数相加减,未知字母及指数不变。
(整式的加减法即合并同类项)
知识回顾
联想整式加减运算中的合并同类项,结合二次根式的相关知识,计算:
(4)解:
探索新知一
(1)二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(3)合并同类二次根式:将同类二次根式的
系数相加减,被开方数和根指数不变.
(2)被开方数相同的最简二次根式叫同类二次根式.
二次根式的加减即为合并同类二次根式。
知识归纳:
将“最简”去掉可以吗?
及时应用:
1、已知4x2+y2-4x-6y+10=0,
求
的值.
拓展应用:
2、
拓展应用:
探索新知二
归纳:
整式运算中的x、y、z是一种字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算规律也适用于二次根式。
拓展应用:
拓展应用:
二次根式的混合运算顺序与整式的混合运算
顺序一样,即先乘方,再乘除,最后加减,
有括号的先算括号里面的。各种运算律依然
适用。
二次根式运算的结果要求:
(1)被开方数不含分母
(2)被开方数不含能开尽方的因数或因式
(3)分母不含二次根式
知识小结:
1、比较大小:
2、计算:
(2)、
(1)、
(3)、
(4)、
(5)、
巩固练习:
1、要焊接如图所示的钢架,大约需要多少米钢材(精确到0.1米)?
m
m
应用练习:
2、小洪做了两张大小不同的正方形壁画送给小海,其中一张面积为800cm2,另一张面积为450cm2,他想如果再用彩带把壁画的边框镶上会更美观。他现在有1.2m长的彩带,请你帮他算一算,他的彩带够用吗?如果不够,还需买多长的彩带?(结果保留整数)
3、已知a、b、c满足
.
(1)求a、b、c的值.(2)试问以a、b、c为边能否构成三角形?若能构成,求出三角形的周长;若不能构成,请说明理由。
3、已知a、b、c满足
.
(1)求a、b、c的值.(2)试问以a、b、c为边能否构成三角形?若能构成,求出三角形的周长;若不能构成,请说明理由。
4、如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?P、Q的距离是多少厘米?(结果用最简二次根式表示)
解:设x
秒后△PBQ的面积为35平方厘米.
则有PB=x
,BQ=2x
.
PQ=
1.二次根式
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
⑵什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根。
⑴什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则
这个数就叫做a的平方根。
0的算术平方根平方根是0.
温故知新
a的平方根是±
a
用
(a≥0)表示。
a
正数有两个平方根且互为相反数;
0有一个平方根就是0;
负数没有平方根。
(3)平方根的性质:
1、16的平方根是什么?
算术平方根是什么?
2、0的平方根是什么?算术平方根是什么?
3、-7有没有平方根?有没有算术平方根?
正数和0都有算术平方根;
负数没有算术平方根。
思考:
50米
a米
塔座所形成的这个直角三角形的
斜边长为__________米。
?米
塔座
a2+2500
新课导入
S
圆形的下球体在平面图上的面积为S,
则半径为_____.
球体
S
π
新课导入
如图所示的值表示正方形的面积,则
正方形的边长是
b-3
表示一些正数的算术平方根.
你认为所得的各代数式有哪些共同特点?
b-3
新课导入
a2+2500
S
π
b-3
归纳:
a2+2500
S
π
b-3
形如
(a≥0)的式子叫二次根式。
a
a叫被开方数.
请你凭着自己已有的知识,说说对二次根式的认识!
1、表示a的算术平方根;
形如
(a≥0)的式子叫二次根式。
a
理解:
2、a可以是数,也可以是式;
3、形式上含有二次根号
;
4、双重非负性:a≥0,
≥0;
a
5、既可表示开方运算,也可表示运算的结果.
1、下列各式是二次根式吗?
?
巩固认识
(1)
32
(2)
-12
(3)
16
(4)
-m
(m≤0)
(5)
xy
(x、y异号)
(6)
a2+1
?
?
(7)
3
5
在实数范围内,负数没有平方根.
(8)
a2+2a+2
?
?
(9)
(m-3)2
2、求下列二次根式中字母的取值范围:
求二次根式中字母的取值范围的基本依据:
①被开方数不小于零;
②分母中有字母时,要保证分母不为零。
(1)
a+1
(3)
(a-3)2
1
1-2a
(4)
(2)
-2x
1
x2
(5)
3
3、若
=0,则
=
。
a-2
+
2b-7
a+2b
4、已知a、b为实数,且满足a=
+1
则a+b的值为
。
1-2b
+
2b-1
5、2+
的最小值为
,此时x的值为
。
3-x
6、已知
与
互为相反数,
则a=
,b=
。
a-b+6
a+b-8
=2
新知探究二
(
2
)2
(
4
)2
=4
(
17
)2
=17
1
3
(
)2
1
3
=
(
0
)2
=0
2
是2的算术平方根,根据算术平方根的意义,
2
是一个平方等于2的非负数,因此:
(
2
)2=2
即:一个非负数的算数平方根的平方
等于非负数本身。
一般地,二次根式有如下性质:
归纳:
(1)
≥0
(a≥0);
a
(2)(
a
)2=
a
(a≥0).
(2)对于
理解:
(1)
(a≥0)
a
表示非负数a的算术平方根.
也就是说,
(a≥0)
a
是一个非负数,它的
平方等于a;
(
a
)2=
a
(a≥0)
利用这一公式
可计算,如:
(
3
2
)2=32×
(
2
)2=9×2=18
如果把该公式反过来就是:
a=(
a
)2
其意义是:可以把任意非负数写成平方的形式。
如:
2=(
2
)2
a-b=(
a-b
)2
(a≥b)
1、你能把下列各数写成某个数的平方或
平方的相反数吗?
(1)
3
(2)
0.5
(3)
-5
(4)
a-b
例题解析:
解:
(1)
3=
(
3
)2
(2)
0.5=
(
0.5
)2
(3)
-5=
-(
5
)2
25,16呢?
(4)
a-b=
(
a-b
)2
(a≥b)
-(
b-a
)2
(a≤b)
例题解析:
2、计算:(1)
(2)
(
8
5
)2
2
7
(-7
)2
解:
(1)
(
8
5
)2
=
82×(
5
)2
=64×5
=320
2
7
(-7
)2
(2)
2
7
×(
)2
=
(-7)2
=49×
2
7
=14
评析:本题直接应用二次根式的性质
求解。当底数是积时,先用积的乘方法则计算,再运用二次根式的性质。
(
a
)2=
a(a≥0)
新知探究三
22
=
2
0.12
=
0.1
2
3
(-
)2
=
2
3
02
=
0
一般地,根据算术平方根的意义,得
a2
=|
a
|
即:一个任意数的平方的算术平方根等于
它本身的绝对值。
比较
和
1、从运算顺序来看:
先开方,后平方;
a2
(
a
)2
(
a
)2
a2
先平方,后开方。
2、从取值范围来看:
(
a
)2中,
a≥0;
a2中,
a取任何实数。
3、从运算结果来看:
(
a
)2=
a
(a≥0)
a2
=|
a
|=
a
(a≥0)
-a
(a<0)
解:(1)∵a≥1,∴a-1≥0,
例题解析:
计算:(1)
(2)
(a-1)2
(a≥1)
(3.14-π)2
∴
(a-1)2
=
|a-1
|=a-1.
(2)∵3.14<π,∴3.14-π<0,
∴
(3.14-π)2
=
|3.14-π
|=π-3.14.
评析:在计算时,为确保计算的正确性,计算
形如
的二次根式时,先要写成
的形式,
再看底数a的符号,防止出现当a<0时,
这样的错误。
a2
a2
=|a|
a2
=a
1、化简下列各式:
巩固认识
(
3
2
)2
+
(1)
(
2
3
)2
(2)
(-5)2
+
(
5
)2
(3)
m2-16m+64
(m<8)
(4)
a2b2
(a<0,
b<0
)
2、实数p在数轴上的位置如图所示,
化简:
(1-p)2
+
(
2-
p
)2
-1
0
1
p
2
3、已知a、b、c为△ABC的三边长,
化简:
(a-b-c)2
+
(b-a+c)2
1.
二次根式的概念
2.二次根式的基本性质
3.
二次根式的重要性质
知识小结
形如
(a≥0)的式子叫二次根式.
a
(1)
≥0
(a≥0);
a
a2
=|
a
|=
a
(a≥0)
-a
(a<0)
(
a
)2=
a
4.
注意
和
的区别与联系.
a2
=
a
(2)(
a
)2=
a
(a≥0).
5.
注意灵活应用二次根式的性质.
课后练习
1、计算:(1)
(
8
)2
+
(
-
3
)2
(2)
-(
-
10
)2
-(
-
3
3
)2
(3)
(
2
5
)2
2
5
-
(-
5
)2
(4)
(
x
xy
)2
-
·
(-y)2
x6
2、若1<x<4,化简代数式:
(x-4)2
+
(x-1)2
3、设a、b、c为△ABC的三边,化简:
(a+b+c)2
+
(a-b-c)2
+
(c-b+a)2
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.1二次根式的乘除法
知识回顾
1、二次根式
(a≥0)是非负数,
.当a≥0时,
=
;
当a<0时,
=
.
a
a
-a
2、单项式与单项式相乘,将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
知识应用
1、已知a<0<b,且∣a∣>∣b∣,那么
的化简结果为
.
2、计算:(1)3x2·(-2xy2)=
;
(2)(5×103)·(-3×102)=
.
0
-6x3y2
-1.5×106
探索1
1、认真观察:
2、模仿计算:
4
7
28
28
28
6
5
30
30
30
12
12
12
12
3、根据上面的结果,直接用“>、<或=”填空:
=
=
=
=
=
=
4、归纳:
=
当a≥0,b≥0时,
即二次根式的乘法法则为:
两个二次根式相乘,将它们的被开方数相乘。
5、应用:
4
利用法则直接写出结果:
-15
-60
6、拓展:
二次根式的乘法公式法则可以推广到多个二次根式相乘的运算.
如:计算
6×15×10
30
探索2
将
反过来,就得到
积的算术平方根,等于积中各因式的算术平方根的积.
积的算术平方根的应用
化简二次根式
如:
模仿上面的方法,化简:
9
2
9
2
拓展应用
(2)将根号外的因式移到根号内:
拓展应用
※拓展应用
比一比,看谁更快!
一、计算:
二、化简:
(2)
3、已知a、b为正实数,下列等式中,
一定成立的是(
)
B
4、下面的解题方法、过程对吗?
5、比较下列各组数的大小:
而20<27,
<
小
结
本节课要掌握:
(a≥0,b≥0)
(a≥0,b≥0)
对于二次根式的乘法及积的算术平方根的化简要灵活运用
课后练习
认真完成导学案的“课后练习题案”.
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.2二次根式的乘除法
温故知新
1、二次根式的乘法法则:两个二次根式相乘,
将它们的被开方数相乘。
用字母表示为:
推广到多个二次根式相乘:
2、积的算术平方根,等于积中各因式的
算术平方根的积.
用字母表示为:
计算化简:
12
知识应用
1、观察:
2、模仿:
探索一
3、根据上面的结果,直接用“>、<或=”填空:
=
=
=
=
=
=
4、归纳:
当a≥0,b>0时,
即二次根式的除法法则为:
两个二次根式相除,将它们的被开方数相除,再取商的算术平方根。
5、应用:
1.利用法则直接写出结果:
2.计算并化简结果:
注意:此处可不用括号
商的算术平方根,等于被除数和除数的算术平方根的商.
将
(a≥0,b>0)反过来,得:
(a≥0,b>0)
探索二
商的算术平方根的应用:
化简二次根式
如:
模仿上面的方法,化简:
解:
拓展应用
比一比,看谁更快!
计算化简:
知识拓展
学了本节知识后,小莉对小明提出了一个问题:“你能运用二次根式的除法法则比较下面两个式子的大小吗?”
同学们,你能帮小明解决这个问题吗?
看看谁的方法更好、更多!
知识拓展
学了本节知识后,小莉对小明提出了一个问题:“你能运用二次根式的除法法则比较下面两个式子的大小吗?”
方法一:规律法
方法二:求差法
方法三:运用乘法法则
方法四:乘方法
本节课要掌握:
(a≥0,b>0)
(a≥0,b>0)
对于二次根式的除法及商的算术平方根的化简要灵活运用
1、
2、
知识小结
课后作业
一、填空题:
1、分母有理化:
2、已知三角形的面积为
cm2,一边长
为
cm,则该边上的高是_____cm.
二、计算化简:
(m>0,
n>0)
(a>0)
三、解答题:
1、先化简下面的式子:
,
然后选择一个合适的x值,
代入化简后的式子求值。
2、站在海拔高度h米的地方,看见的水平距
离是d米,它们之间近似地符合公式
.
某一登山者从海拔n米登上海拔2n米的山顶,
那么他看到的水平距离是原来的多少倍?
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
2.3二次根式的乘除法
.
1、当a≥0,b≥0时,
;
反之,
2、当a≥0,b>0时,
;反之,
3、二次根式的乘除法及积(商)的算术平方根在具体问题中灵活使用,结果要化简.
4、把分母中含有的根号去掉的过程叫分母有理化.通过分母有理化,可化简二次根式。
温故知新
一、下面的计算正确吗?若不正确请改正:
知识应用
(a<0,
b<0)
解:都错误,正确的应为:
(2)∵a<0,
b<0,
二、计算化简:
解:
二、计算化简:
解:
1、计算:
2、观察上面计算题的最后结果,可以发现这些式子中的二次根式两个特点:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或
因式.
探索
3、归纳:
同时满足下列两个条件的二次根式是最简二次根式:
(1)被开方数不含分母(即被开方数中因数是整数,因式是整式);
(2)被开方数不含能开得尽方的因数或因式(即被开方数的因数或因式的幂的指数都小于2)
下列各式中是最简二次根式的是(
)
D
及时反馈
下列各式中是最简二次根式的是(
)
D
≠
切记
及时反馈
应用:
1、把下面的二次根式化为最简二次根式:
解:
2、如图,在Rt△ABC中,∠C=90?,
AC=2.5cm,BC=6cm,求AB的长.
B
C
A
解:由题意得
拓展:
解:
解:
解:
小
结
本节课要掌握:
2、利用分母有理化对含分母的二次根式进行化简.
1、最简二次根式的两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.
课后作业
1、化简:
(x>0)
2、已知a为实数,化简
阅读下面的解答过程,请判断是否正确?若不正确,请写出正确的解答过程:
解:
3、已知一个矩形的长为
,宽
为
,与它面积相等的圆的
半径为多少?
4、利用分母有理化巧算:
华东师大版九年级上学期
第21章
《二次根式》
学而不疑则怠,疑而不探则空
3.二次根式的加减法
1、最简二次根式的被开方数要满足两个条件:(1)不含分母;(2)不含能开得尽方的因数或因式。
2、同类项:含有相同的字母,并且相同字母的指数分别相同的项叫同类项。
3、合并同类项:将同类项的系数相加减,未知字母及指数不变。
(整式的加减法即合并同类项)
知识回顾
联想整式加减运算中的合并同类项,结合二次根式的相关知识,计算:
(4)解:
探索新知一
(1)二次根式加减时,先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(3)合并同类二次根式:将同类二次根式的
系数相加减,被开方数和根指数不变.
(2)被开方数相同的最简二次根式叫同类二次根式.
二次根式的加减即为合并同类二次根式。
知识归纳:
将“最简”去掉可以吗?
及时应用:
1、已知4x2+y2-4x-6y+10=0,
求
的值.
拓展应用:
2、
拓展应用:
探索新知二
归纳:
整式运算中的x、y、z是一种字母,它的意义十分广泛,可以代表所有一切,当然也可以代表二次根式,所以,整式中的运算规律也适用于二次根式。
拓展应用:
拓展应用:
二次根式的混合运算顺序与整式的混合运算
顺序一样,即先乘方,再乘除,最后加减,
有括号的先算括号里面的。各种运算律依然
适用。
二次根式运算的结果要求:
(1)被开方数不含分母
(2)被开方数不含能开尽方的因数或因式
(3)分母不含二次根式
知识小结:
1、比较大小:
2、计算:
(2)、
(1)、
(3)、
(4)、
(5)、
巩固练习:
1、要焊接如图所示的钢架,大约需要多少米钢材(精确到0.1米)?
m
m
应用练习:
2、小洪做了两张大小不同的正方形壁画送给小海,其中一张面积为800cm2,另一张面积为450cm2,他想如果再用彩带把壁画的边框镶上会更美观。他现在有1.2m长的彩带,请你帮他算一算,他的彩带够用吗?如果不够,还需买多长的彩带?(结果保留整数)
3、已知a、b、c满足
.
(1)求a、b、c的值.(2)试问以a、b、c为边能否构成三角形?若能构成,求出三角形的周长;若不能构成,请说明理由。
3、已知a、b、c满足
.
(1)求a、b、c的值.(2)试问以a、b、c为边能否构成三角形?若能构成,求出三角形的周长;若不能构成,请说明理由。
4、如图所示的Rt△ABC中,∠B=90°,点P从点B开始沿BA边以1厘米/秒的速度向点A移动;同时,点Q也从点B开始沿BC边以2厘米/秒的速度向点C移动.问:几秒后△PBQ的面积为35平方厘米?P、Q的距离是多少厘米?(结果用最简二次根式表示)
解:设x
秒后△PBQ的面积为35平方厘米.
则有PB=x
,BQ=2x
.
PQ=
