华东师大版七年级下册数学 9.1 .3三角形的三边关系 课件(共20张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 9.1 .3三角形的三边关系 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 578.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
9.1.3
三角形的三边关系
1.了解三角形的稳定性。
2.初步认识三角形的作法。
3.掌握三角形的三边关系。
学习目标
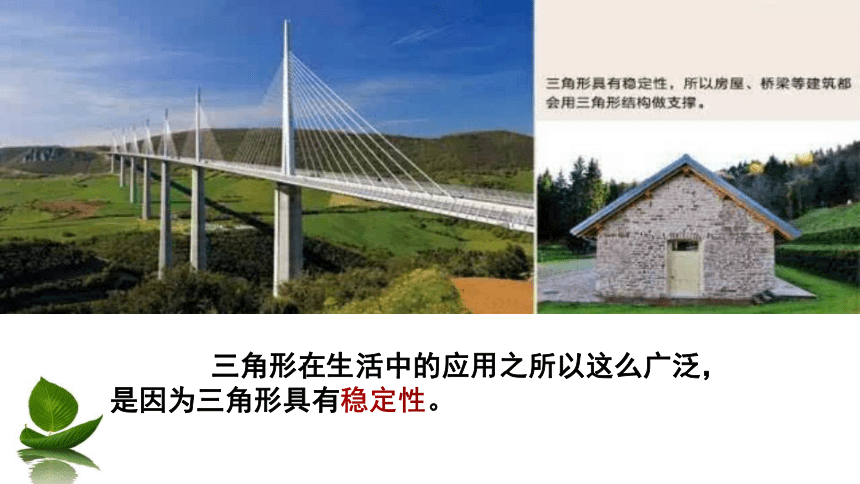
三角形在生活中的应用之所以这么广泛,是因为三角形具有稳定性。
三角形的稳定性具体指的是什么意思?
三角形的稳定性:
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.
性质了解
1、下列图形中具有稳定性的是(
)
(A)正方形
(B)长方形
(C)直角三角形
(D)平行四边形
C
跟踪训练
2、要使下列木架稳定各至少需要多少根木棍?
跟踪训练
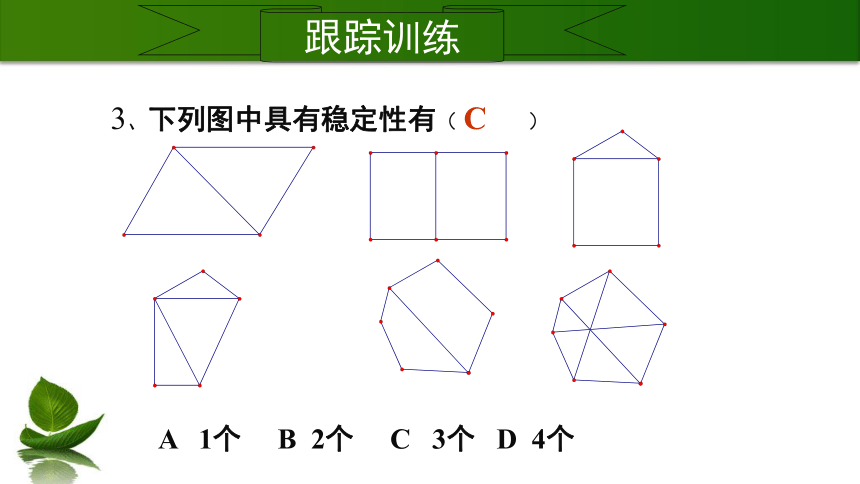
3、下列图中具有稳定性有(
)
A
1个
B
2个
C
3个
D
4个
C
做一做
画一个三角形,使它的三条边长分别是4cm、3cm、2.5cm。
B
A
C
作法:
1.画线段AB=4cm。
2.以点A为圆心、3cm为半径画弧。
3.再以点B为圆心、2.5cm为半径画弧。
4.两弧相交于点C,连结AC、BC。
此时,所得的图形就是△ABC。
实践操作
现有两条线段,长度分别是2cm和3cm,请同学们用4cm、5cm、6cm长的线段做底边,看一看能否作出三角形。
根据以上画法,
作完图后你会发
现下列三种不同
的情况。
三边关系
a+b>c
b+c>a
a+c>b
换句话说:在三角形中
三角形的任何两边之和大于第三边。
也就是说,若任意两条较短线段之和大于第三条线段,则
这三条线段就能构成一个三角形。
。
因此,并不是任意三条线段都可以组成一个三角形.在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
跟踪训练
做题技巧:在判断一组数据能否组成三角形时,只要看一看两条较短线段之和是否大于第三条线段。
(3)3
cm、8
cm、5
cm;
(4)4
cm、5
cm、6
cm.
(1)
15cm、10
cm、7
cm;
(2)4
cm、5
cm、10
cm;
1.下列长度的各组线段能否组成一个三角形?
√
×
×
√
三边关系
|a-b|<c
|a-c|<b
|b-c|<a
。
在三角形中,还有一种关系。
三角形的任何两边之差的绝对值小于第三边。
想一想
已知三角形的两边a、b长分别为
9、5,则第三边c的取值范围 。
三角形的任何两边之差的绝对值小于第三边。
|a-b|<
c<a+b
依据:三角形的任何两边之和大于第三边。
鲁班给徒弟两根树,一根长8米,另一根长12米,要想做一个三角形屋架,请你帮徒弟想一想,第三根树应多长?
解:根据题意可得。
|12-8|
<c<12+8
即
8
<c<20
答:第三树应大于8米小于20米。
议一议
1、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。
(
)
2、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为
。
3、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差
。
2
?
20
跟踪训练
自我反思
课本P82:
练
习
第1.2题
习题9.1
第1-4题
请同学们认真完成!!!
课后作业
再见
9.1.3
三角形的三边关系
1.了解三角形的稳定性。
2.初步认识三角形的作法。
3.掌握三角形的三边关系。
学习目标
三角形在生活中的应用之所以这么广泛,是因为三角形具有稳定性。
三角形的稳定性具体指的是什么意思?
三角形的稳定性:
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.
性质了解
1、下列图形中具有稳定性的是(
)
(A)正方形
(B)长方形
(C)直角三角形
(D)平行四边形
C
跟踪训练
2、要使下列木架稳定各至少需要多少根木棍?
跟踪训练
3、下列图中具有稳定性有(
)
A
1个
B
2个
C
3个
D
4个
C
做一做
画一个三角形,使它的三条边长分别是4cm、3cm、2.5cm。
B
A
C
作法:
1.画线段AB=4cm。
2.以点A为圆心、3cm为半径画弧。
3.再以点B为圆心、2.5cm为半径画弧。
4.两弧相交于点C,连结AC、BC。
此时,所得的图形就是△ABC。
实践操作
现有两条线段,长度分别是2cm和3cm,请同学们用4cm、5cm、6cm长的线段做底边,看一看能否作出三角形。
根据以上画法,
作完图后你会发
现下列三种不同
的情况。
三边关系
a+b>c
b+c>a
a+c>b
换句话说:在三角形中
三角形的任何两边之和大于第三边。
也就是说,若任意两条较短线段之和大于第三条线段,则
这三条线段就能构成一个三角形。
。
因此,并不是任意三条线段都可以组成一个三角形.在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
跟踪训练
做题技巧:在判断一组数据能否组成三角形时,只要看一看两条较短线段之和是否大于第三条线段。
(3)3
cm、8
cm、5
cm;
(4)4
cm、5
cm、6
cm.
(1)
15cm、10
cm、7
cm;
(2)4
cm、5
cm、10
cm;
1.下列长度的各组线段能否组成一个三角形?
√
×
×
√
三边关系
|a-b|<c
|a-c|<b
|b-c|<a
。
在三角形中,还有一种关系。
三角形的任何两边之差的绝对值小于第三边。
想一想
已知三角形的两边a、b长分别为
9、5,则第三边c的取值范围 。
三角形的任何两边之差的绝对值小于第三边。
|a-b|<
c<a+b
依据:三角形的任何两边之和大于第三边。
鲁班给徒弟两根树,一根长8米,另一根长12米,要想做一个三角形屋架,请你帮徒弟想一想,第三根树应多长?
解:根据题意可得。
|12-8|
<c<12+8
即
8
<c<20
答:第三树应大于8米小于20米。
议一议
1、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。
(
)
2、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为
。
3、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差
。
2
?
20
跟踪训练
自我反思
课本P82:
练
习
第1.2题
习题9.1
第1-4题
请同学们认真完成!!!
课后作业
再见
