人教版八年级数学上册课件:11.2.1三角形的内角(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:11.2.1三角形的内角(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 19:49:31 | ||
图片预览





文档简介
(共18张PPT)
11.2.1
三角形的内角
一、激发求知欲
1。什么样的图形称作三角形?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2。三角形的表示。如图
三角形ABC表示为△ABC
A
B
C
边
顶点
内角
3.三角形三边的关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
二、展示目标和任务
1.目标
掌握三角形内角和定理,直角三角形的性质
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
体会数学与现实生活的联系,增强克服困难的勇气和信心
2.任务
掌握并学会证明三角形内角和定理,利用三角形内角和及直角三角形的性质解知一角求两角的题型
三、自主合作与交流
1。三角形的三个内角有什么关系?
答:三角形的三个内角和等于180°
2。你是怎么得到的?动手做一做。
拿出准备的三角形,然后如图一样标上三角形的三个内角,把三角形的三个内角撕下来,拼一拼,看看能否得到你们的结论。
1
2
3
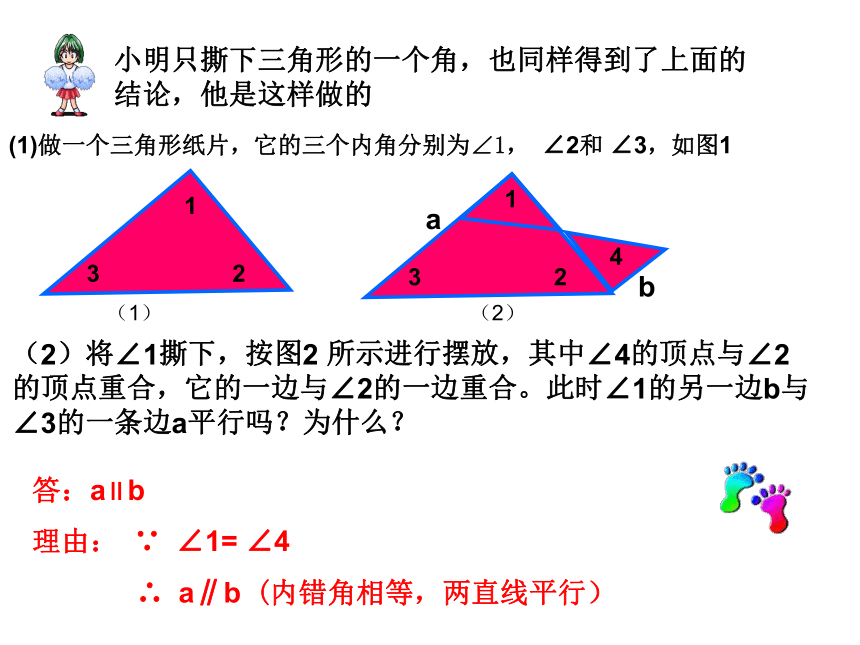
小明只撕下三角形的一个角,也同样得到了上面的结论,他是这样做的
(1)做一个三角形纸片,它的三个内角分别为∠1,
∠2和
∠3,如图1
1
3
2
答:a∥b
理由:
∵
∠1=
∠4
∴
a∥b
(内错角相等,两直线平行)
(1)
3
2
4
(2)将∠1撕下,按图2
所示进行摆放,其中∠4的顶点与∠2的顶点重合,它的一边与∠2的一边重合。此时∠1的另一边b与∠3的一条边a平行吗?为什么?
a
b
1
(2)
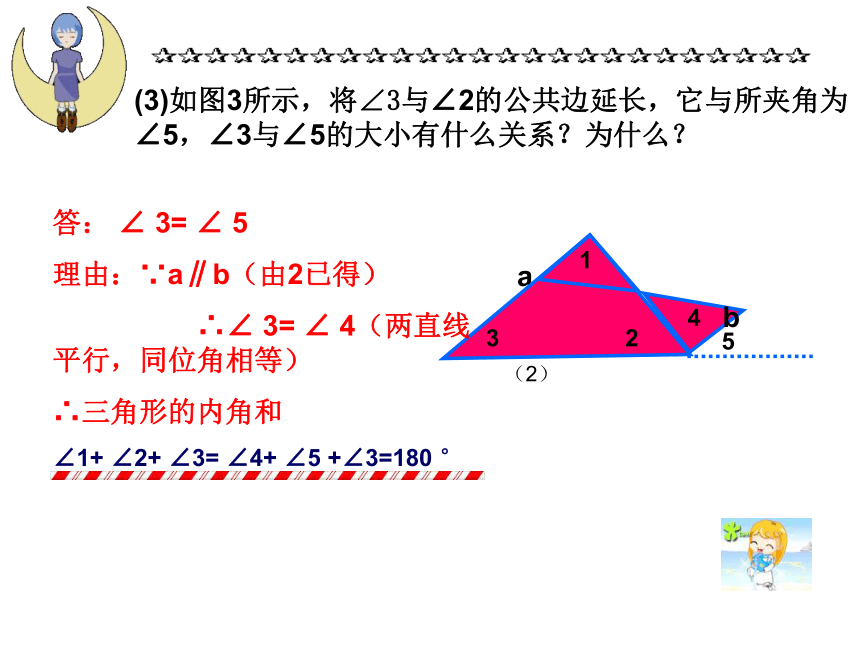
(3)如图3所示,将∠3与∠2的公共边延长,它与所夹角为∠5,∠3与∠5的大小有什么关系?为什么?
a
(2)
3
2
4
b
1
5
答:
∠
3=
∠
5
理由:∵a∥b(由2已得)
∴∠
3=
∠
4(两直线平行,同位角相等)
∴三角形的内角和
∠1+
∠2+
∠3=
∠4+
∠5
+∠3=180
°
变式:已知EF∥BC.
求证:∠BAC+∠B+∠C=180°
A
B
C
E
F
证明:∵EF∥BC
∴∠EAB=∠B,∠FAC=∠C
又∵∠BAC+∠EAB+∠FAC=180°
∴∠BAC+∠B+∠C=180°
四、成果展示,教师点拨
三角形的内角和等于180°
即:△ABC如图所示,三角形的三个内角的和
∠A+∠B+∠C=180°
A
B
C
例题讲解
例1.在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数?
例2.如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西50°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看、B两岛的视角∠ACB呢?
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”如图所示
C
A
B
把直角所对的边称为斜边
夹直角的两条边称为直角边
直角边
直角边
斜边
直角三角形有许多性质,你能发现它的两个锐角之间有什么关系吗?
发现:两锐角互余
∵
Rt△ABC中∠C=90°
且
∠A+
∠B+
∠C=180°(三角形内角和等于180°)
∴
∠A+
∠B=180°—
∠C=90
°
结论2
直角三角形的两个锐角互余
随堂练习:
1.在△ABC中,∠A=90°,∠B=∠C,求∠C的度数.
解:在△ABC中,∵
∠A=90°,∠B=∠C(已知)
且∠A+∠B+∠C=180
°(三角形的内角和等于180°)
∴
∠B+∠C=180°—∠A=180°—90°=90°
∵
∠B=∠C
(已知)
∴∠B=∠C=45°
思考:直角三角形的两个锐角互余,反过来,有两个角互余的三角形是直角三角形吗?
2。观察下面的三角形,并把它们的标号填入相应的括号内
①
②
③
④
⑤
⑥
⑦
锐角三角形
直角三角形
钝角三角形
③
⑤
①
④
⑥
②
⑦
3。一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30
°和60
°
(2)40
°和70
°
(3)50
°和20°
直角三角形
锐角三角形
钝角三角形
小结
1。三角形的内角和等于180°。
2。三角形的分类。
3。直角三角形的两锐角互余。
课后思考
11.2.1
三角形的内角
天生我才
4.如图,在Rt△ABC中,∠BAC=90°,作BC边上的高AD,图中出现多少个Rt△?又作△ABD中AB边的高DD1,这时图中出现多少个Rt△?照同样的作法作下去,作出D1D2、D2D3、······当作出Dn-1Dn时,图中共出现多少个Rt△?
A
C
B
D
D1
D2
D3
D4
课后思考
11.2.1
三角形的内角
天生我才
5.如图,BD、CD都是△ABC的角平分线且交点为D,试探索∠BDC和∠A之间的数量关系.
A
B
C
D
再见!
11.2.1
三角形的内角
一、激发求知欲
1。什么样的图形称作三角形?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2。三角形的表示。如图
三角形ABC表示为△ABC
A
B
C
边
顶点
内角
3.三角形三边的关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
二、展示目标和任务
1.目标
掌握三角形内角和定理,直角三角形的性质
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
体会数学与现实生活的联系,增强克服困难的勇气和信心
2.任务
掌握并学会证明三角形内角和定理,利用三角形内角和及直角三角形的性质解知一角求两角的题型
三、自主合作与交流
1。三角形的三个内角有什么关系?
答:三角形的三个内角和等于180°
2。你是怎么得到的?动手做一做。
拿出准备的三角形,然后如图一样标上三角形的三个内角,把三角形的三个内角撕下来,拼一拼,看看能否得到你们的结论。
1
2
3
小明只撕下三角形的一个角,也同样得到了上面的结论,他是这样做的
(1)做一个三角形纸片,它的三个内角分别为∠1,
∠2和
∠3,如图1
1
3
2
答:a∥b
理由:
∵
∠1=
∠4
∴
a∥b
(内错角相等,两直线平行)
(1)
3
2
4
(2)将∠1撕下,按图2
所示进行摆放,其中∠4的顶点与∠2的顶点重合,它的一边与∠2的一边重合。此时∠1的另一边b与∠3的一条边a平行吗?为什么?
a
b
1
(2)
(3)如图3所示,将∠3与∠2的公共边延长,它与所夹角为∠5,∠3与∠5的大小有什么关系?为什么?
a
(2)
3
2
4
b
1
5
答:
∠
3=
∠
5
理由:∵a∥b(由2已得)
∴∠
3=
∠
4(两直线平行,同位角相等)
∴三角形的内角和
∠1+
∠2+
∠3=
∠4+
∠5
+∠3=180
°
变式:已知EF∥BC.
求证:∠BAC+∠B+∠C=180°
A
B
C
E
F
证明:∵EF∥BC
∴∠EAB=∠B,∠FAC=∠C
又∵∠BAC+∠EAB+∠FAC=180°
∴∠BAC+∠B+∠C=180°
四、成果展示,教师点拨
三角形的内角和等于180°
即:△ABC如图所示,三角形的三个内角的和
∠A+∠B+∠C=180°
A
B
C
例题讲解
例1.在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数?
例2.如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西50°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看、B两岛的视角∠ACB呢?
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”如图所示
C
A
B
把直角所对的边称为斜边
夹直角的两条边称为直角边
直角边
直角边
斜边
直角三角形有许多性质,你能发现它的两个锐角之间有什么关系吗?
发现:两锐角互余
∵
Rt△ABC中∠C=90°
且
∠A+
∠B+
∠C=180°(三角形内角和等于180°)
∴
∠A+
∠B=180°—
∠C=90
°
结论2
直角三角形的两个锐角互余
随堂练习:
1.在△ABC中,∠A=90°,∠B=∠C,求∠C的度数.
解:在△ABC中,∵
∠A=90°,∠B=∠C(已知)
且∠A+∠B+∠C=180
°(三角形的内角和等于180°)
∴
∠B+∠C=180°—∠A=180°—90°=90°
∵
∠B=∠C
(已知)
∴∠B=∠C=45°
思考:直角三角形的两个锐角互余,反过来,有两个角互余的三角形是直角三角形吗?
2。观察下面的三角形,并把它们的标号填入相应的括号内
①
②
③
④
⑤
⑥
⑦
锐角三角形
直角三角形
钝角三角形
③
⑤
①
④
⑥
②
⑦
3。一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30
°和60
°
(2)40
°和70
°
(3)50
°和20°
直角三角形
锐角三角形
钝角三角形
小结
1。三角形的内角和等于180°。
2。三角形的分类。
3。直角三角形的两锐角互余。
课后思考
11.2.1
三角形的内角
天生我才
4.如图,在Rt△ABC中,∠BAC=90°,作BC边上的高AD,图中出现多少个Rt△?又作△ABD中AB边的高DD1,这时图中出现多少个Rt△?照同样的作法作下去,作出D1D2、D2D3、······当作出Dn-1Dn时,图中共出现多少个Rt△?
A
C
B
D
D1
D2
D3
D4
课后思考
11.2.1
三角形的内角
天生我才
5.如图,BD、CD都是△ABC的角平分线且交点为D,试探索∠BDC和∠A之间的数量关系.
A
B
C
D
再见!
