人教版八年级数学上册课件:11.2.2 三角形的外角(共26张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:11.2.2 三角形的外角(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 677.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 19:51:21 | ||
图片预览





文档简介
(共26张PPT)
11.2.2
三角形的外角
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
1
2
3
A
B
C
D
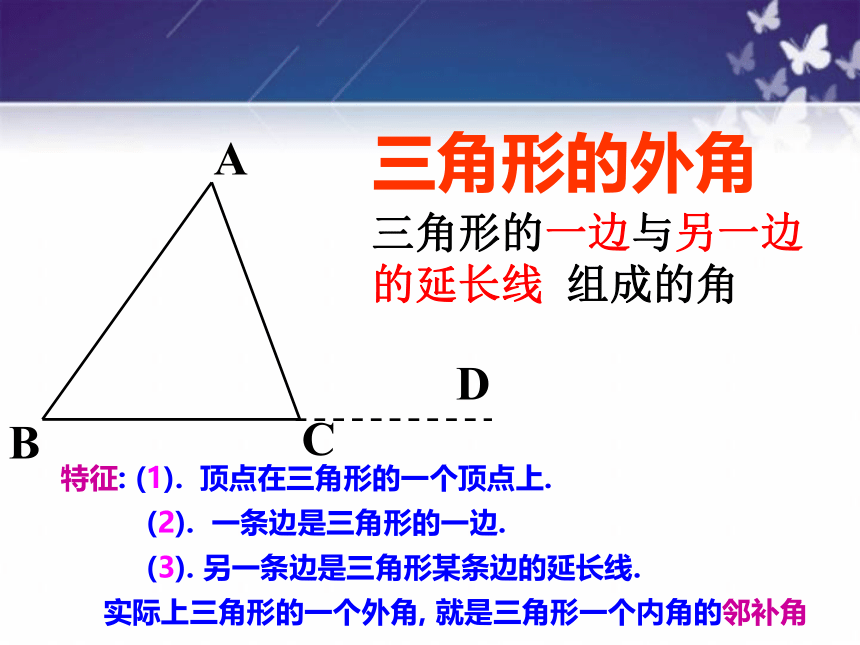
三角形的外角
三角形的一边与另一边
的延长线
组成的角
特征:
(1).
顶点在三角形的一个顶点上.
(2).
一条边是三角形的一边.
(3).
另一条边是三角形某条边的延长线.
实际上三角形的一个外角,
就是三角形一个内角的邻补角
C
A
B
D
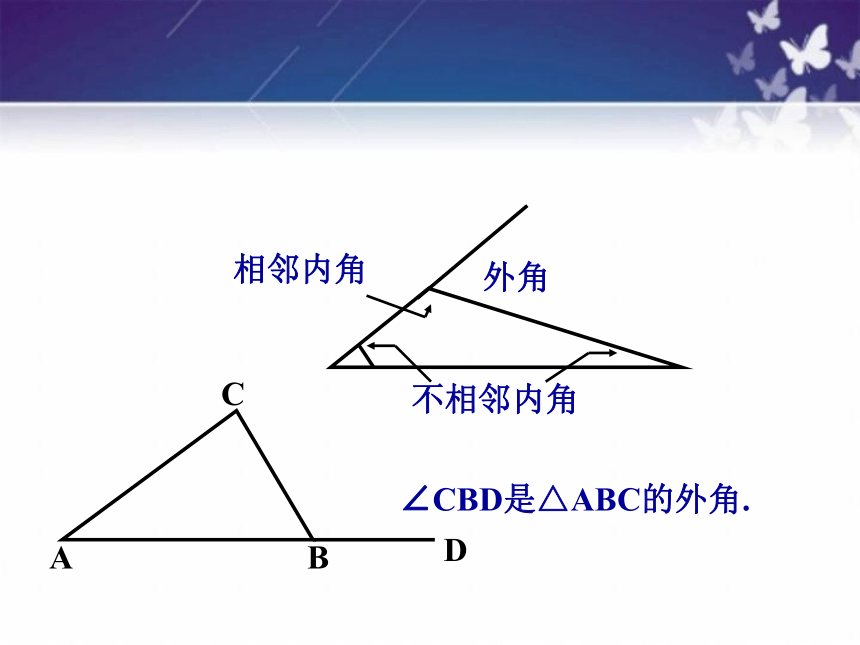
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
画一个△ABC
,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
A
B
C
画一个△ABC
,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
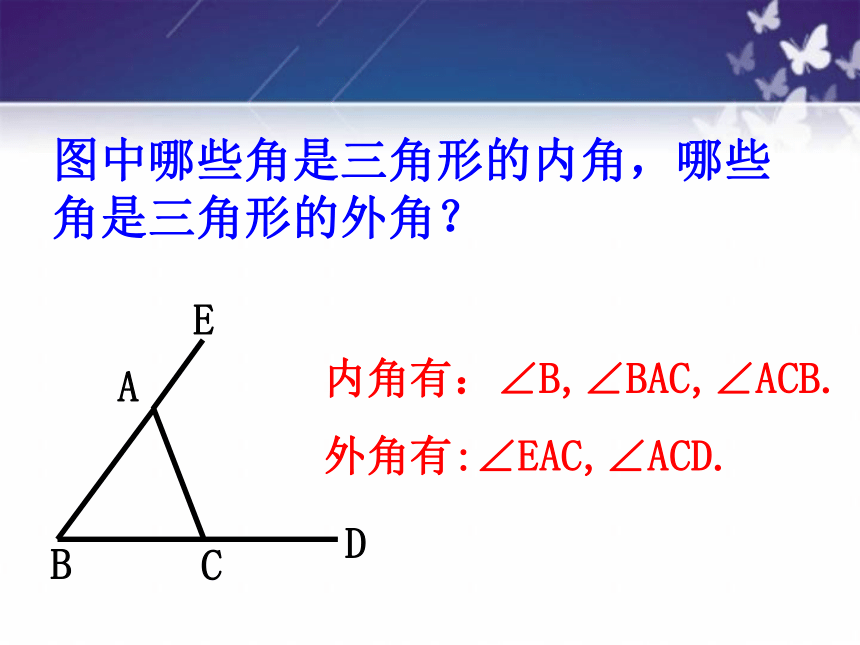
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
内角与外角有什么关系?
(1)
相邻:
C
A
B
D
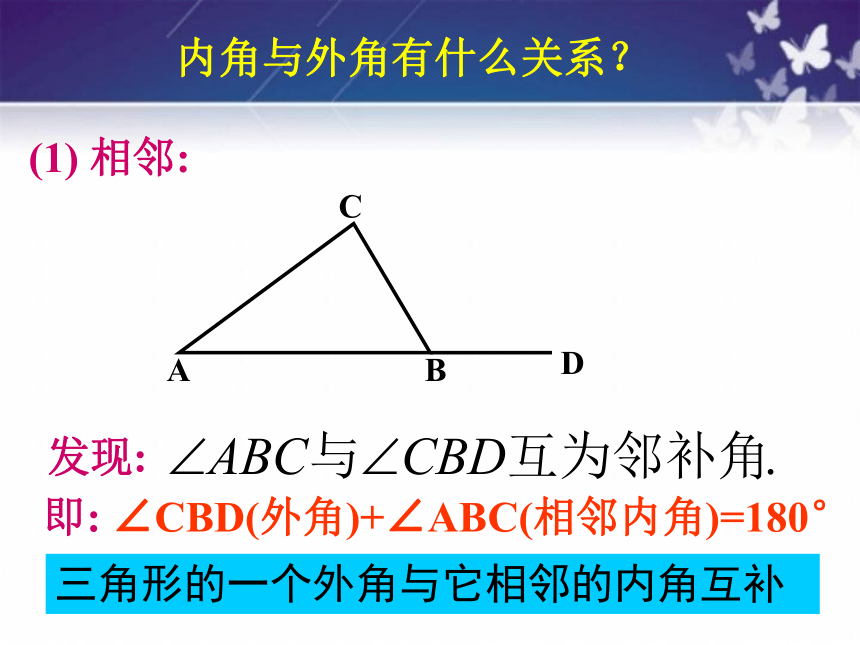
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
三角形的一个外角与它相邻的内角互补
C
A
B
D
(2)
不相邻:
?
∵
∴
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
三角形的一个外角等于与它不相邻的两个内角的和
上面我们通过计算得到了三角形中外角与不相邻两内角之间的数量关系.你能试着用其它的方法加以说明吗?你想到了哪些方法?
议一议
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
三角形的一个外角大于任何一个与它不相邻的内角。
A
C
B
D
>
>
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系
三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
1.求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
90°
95°
85°
2.如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
【答案】(1)40°
(2)
70°
A
B
C
1
2
3
三角形的外角和为360°.
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果?
A
B
C
1
2
3
∠2+
∠ABC=180°,
∠3+
∠ACB=180°,
三个式子相加得到
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°,
而∠BAC+
∠ABC+∠ACB=180°,
故∠1+
∠2+
∠3=360°.
方法一:∠1+
∠BAC=180°,
解:
判断题:
1.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
A
B
C
D
E
F
1
H
2
【例】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴
∠1=∠B+∠D(三角形的一个外角等于与它不相邻的两个内角的和).
∴
∠2=∠C+∠E(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和等于180°),
又∵
∠2是△EHC的一个外角(外角的定义),
∴
∠A+∠B+∠C+∠D+∠E
=180°(等式的性质).
【解析】∵∠1是△BDF的一个外角(外角的定义),
∠A+∠B+∠C+∠D+∠E+∠F=
.
1
2
3
360°
A
B
C
D
E
F
【跟踪训练】
1.已知△ABC的一个外角为50°,则△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
【解析】选B.
△ABC的一个外角为50°,则与这个外角相邻的内角是130°,所以△ABC一定是钝角三角形.
2.
如图,在△ABC中,CD是∠ACB的平分线,∠A
=
80°,∠ACB=60°,那么∠BDC=
( )
A.80°
B.90°
C.100°
D.110°
D
A
B
C
【解析】选D.因为CD是∠ACB的平分线,
所以∠ACD=
×60°=30°,所以
∠BDC=∠A+∠ACD=
80°+
30°=
110°.
3.
一副三角板,如图叠放在一起,∠1的度数是_______度.
75
4.
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=
.
70°
5.已知图中∠A,∠B,∠C分别为80°,20°,30°,求∠1的度数.
B
3
2
1
A
C
D
E
【解析】
∠1=
∠2+
∠B=
∠A+
∠C+
∠B
=
80°+
30°+
20°=
130°.
1.三角形内角和定理的推论.
三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
通过本课时的学习,需要我们掌握:
11.2.2
三角形的外角
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
1
2
3
A
B
C
D
三角形的外角
三角形的一边与另一边
的延长线
组成的角
特征:
(1).
顶点在三角形的一个顶点上.
(2).
一条边是三角形的一边.
(3).
另一条边是三角形某条边的延长线.
实际上三角形的一个外角,
就是三角形一个内角的邻补角
C
A
B
D
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
画一个△ABC
,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
A
B
C
画一个△ABC
,你能画出它的所有外角吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,它们相等.
注:每个外角与相应的内角互为补角.
A
B
C
D
E
图中哪些角是三角形的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
内角与外角有什么关系?
(1)
相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
三角形的一个外角与它相邻的内角互补
C
A
B
D
(2)
不相邻:
?
∵
∴
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
三角形的一个外角等于与它不相邻的两个内角的和
上面我们通过计算得到了三角形中外角与不相邻两内角之间的数量关系.你能试着用其它的方法加以说明吗?你想到了哪些方法?
议一议
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
三角形的一个外角大于任何一个与它不相邻的内角。
A
C
B
D
>
>
2.三角形的一个外角等于与它不相邻的两个内角的和.
1.三角形的一个外角与它相邻的内角互补;
三角形的外角与内角的关系
三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
1.求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
90°
95°
85°
2.如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
【答案】(1)40°
(2)
70°
A
B
C
1
2
3
三角形的外角和为360°.
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果?
A
B
C
1
2
3
∠2+
∠ABC=180°,
∠3+
∠ACB=180°,
三个式子相加得到
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°,
而∠BAC+
∠ABC+∠ACB=180°,
故∠1+
∠2+
∠3=360°.
方法一:∠1+
∠BAC=180°,
解:
判断题:
1.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
A
B
C
D
E
F
1
H
2
【例】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴
∠1=∠B+∠D(三角形的一个外角等于与它不相邻的两个内角的和).
∴
∠2=∠C+∠E(三角形的一个外角等于与它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和等于180°),
又∵
∠2是△EHC的一个外角(外角的定义),
∴
∠A+∠B+∠C+∠D+∠E
=180°(等式的性质).
【解析】∵∠1是△BDF的一个外角(外角的定义),
∠A+∠B+∠C+∠D+∠E+∠F=
.
1
2
3
360°
A
B
C
D
E
F
【跟踪训练】
1.已知△ABC的一个外角为50°,则△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
【解析】选B.
△ABC的一个外角为50°,则与这个外角相邻的内角是130°,所以△ABC一定是钝角三角形.
2.
如图,在△ABC中,CD是∠ACB的平分线,∠A
=
80°,∠ACB=60°,那么∠BDC=
( )
A.80°
B.90°
C.100°
D.110°
D
A
B
C
【解析】选D.因为CD是∠ACB的平分线,
所以∠ACD=
×60°=30°,所以
∠BDC=∠A+∠ACD=
80°+
30°=
110°.
3.
一副三角板,如图叠放在一起,∠1的度数是_______度.
75
4.
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=
.
70°
5.已知图中∠A,∠B,∠C分别为80°,20°,30°,求∠1的度数.
B
3
2
1
A
C
D
E
【解析】
∠1=
∠2+
∠B=
∠A+
∠C+
∠B
=
80°+
30°+
20°=
130°.
1.三角形内角和定理的推论.
三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
通过本课时的学习,需要我们掌握:
