人教版八年级数学上册课件:11.3.2多边形的内角和(共25张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:11.3.2多边形的内角和(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
多边形的内角和
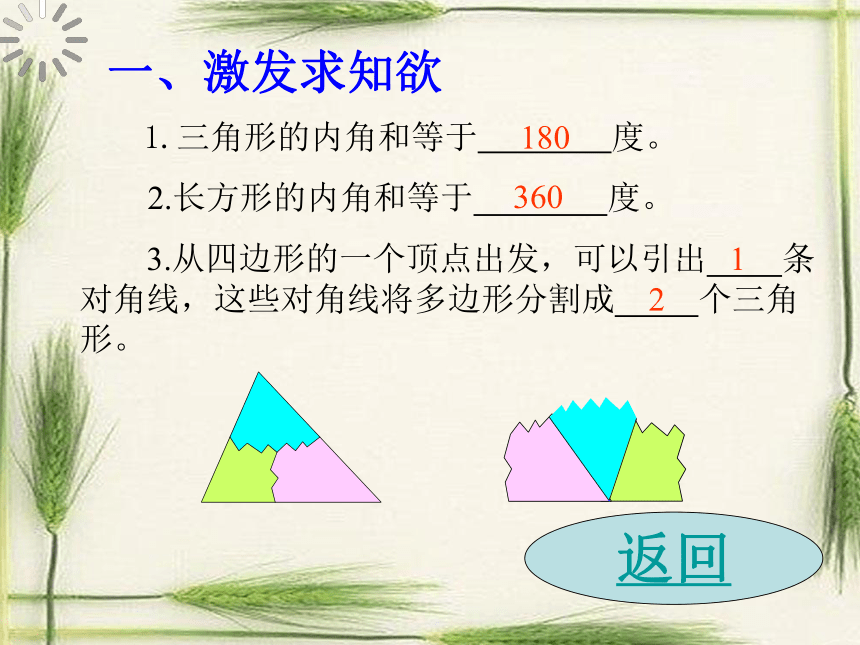
一、激发求知欲
1.三角形的内角和等于
度。
3.从四边形的一个顶点出发,可以引出
条对角线,这些对角线将多边形分割成
个三角形。
2.长方形的内角和等于
度。
1
2
180
360
返回
这些地砖是如何镶嵌的没有缝隙?
二、展示目标和任务
1.学习目标
(1)使学生了解多边形的内角和与外交和等概念。
(2)能通过不同方法探索多边形的内角和及外角和公式,并会应用它们进行有关计算。
2.学习任务
在探索多边形内角和时,学会如何把多边形转化成三角形
;并会利用外角与相邻内角之间的关系求多边形的外角和。
你能不能利用三角形的认识,求出这几个多边形的内角和?
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
以下图中从一个顶点出发可以引出几条对角线?
三、自主合作与交流
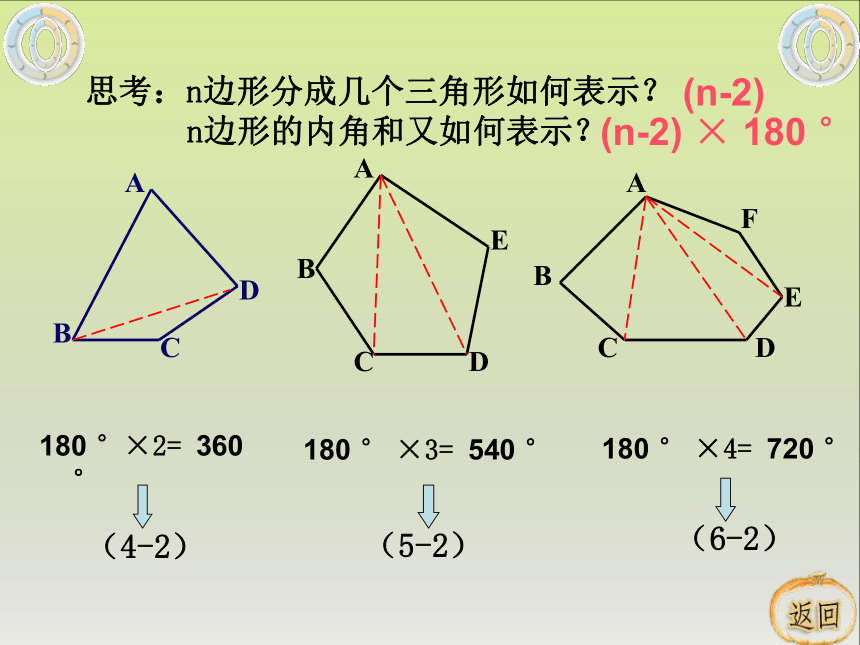
思考:n边形分成几个三角形如何表示?
n边形的内角和又如何表示?
A
B
C
D
B
A
C
E
D
B
F
E
D
C
A
180
°×2=
360
°
180
°
×3=
540
°
180
°
×4=
720
°
(4-2)
(5-2)
(6-2)
(n-2)
(n-2)
×
180
°
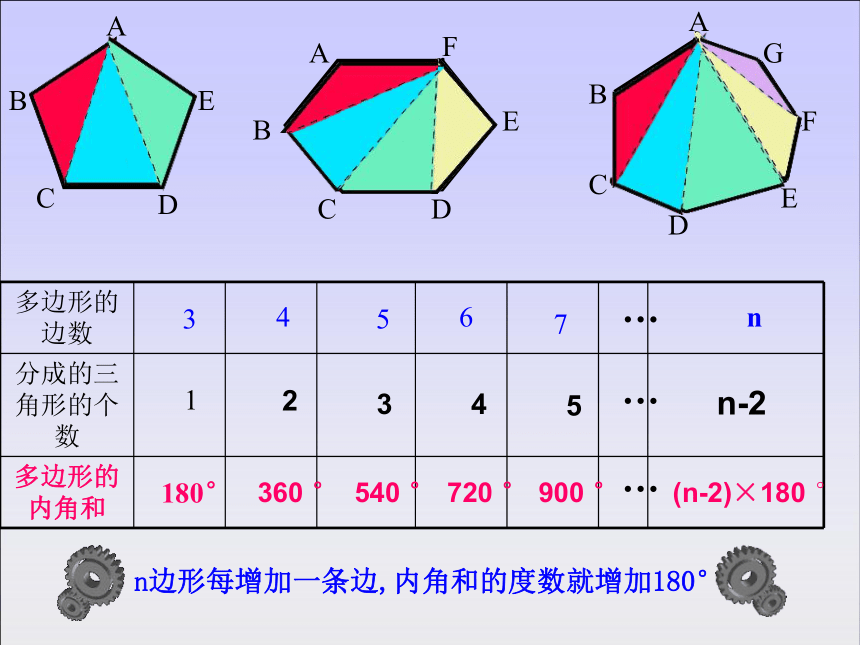
多边形的内角和
分成的三角形的个数
多边形的边数
1
…
180°
…
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
2
3
4
5
n-2
(n-2)×180
°
900
°
720
°
540
°
360
°
n边形每增加一条边,内角和的度数就增加180°
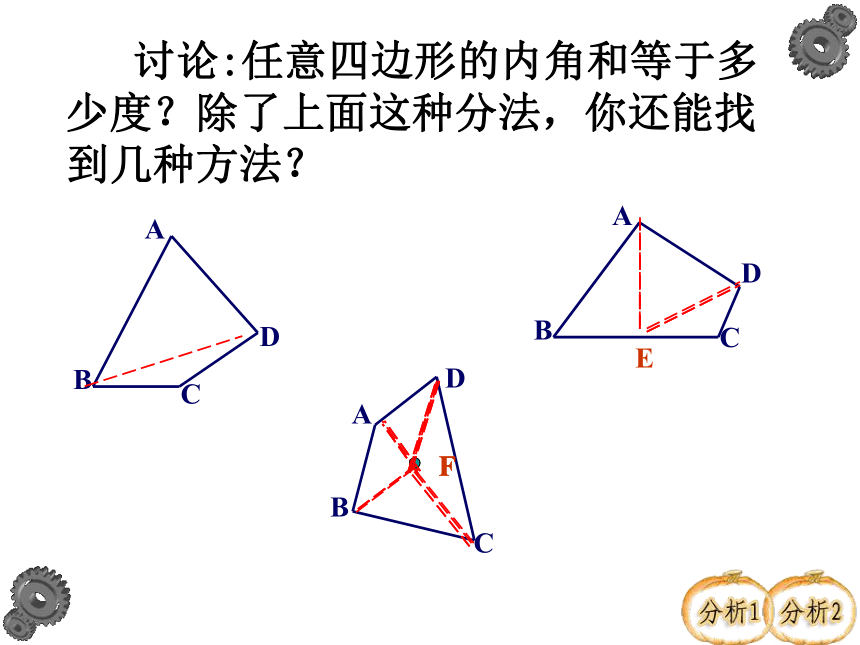
讨论:任意四边形的内角和等于多少度?除了上面这种分法,你还能找到几种方法?
A
B
C
D
F
E
A
B
C
D
A
B
C
D
F
F
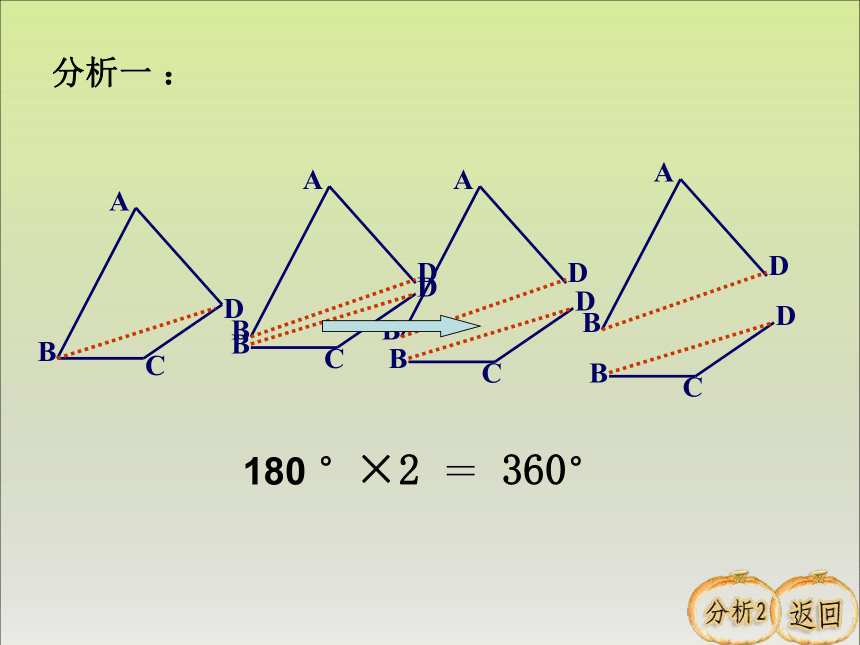
分析一
:
180
°×2
=
360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析二
:
180
°
×3
-180
°=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
想一想:这两种分割方法你又能不能求出多边形的内角和?
1、求八边形的内角和的度数.那七边形的内角和度数又为多少呢?
解:(8-2)×180°=1080°
(7-2)×180°=900°
答:八边形的内角和是1080°.
七边形的内角和是900°.
[提示:
n边形的内角和=
(n-2)×180°]
随堂练习
2、已知一个多边形的内角和等于1440°,求它的边数。
解:设这个多边形的边数为n,根据题意可得:
(n-2)×180°=1440°
解得:
n=10
答:这个多边形是十边形°
例1.如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
A
D
C
B
因为
∠A+∠B+
∠C+
∠D=360°
所以
∠B+
∠D
=360°-(
∠A+∠C
)
=360°-
180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
解:如图所示,四边形ABCD中,
不妨设∠A+∠C=180°
四、成果展示,教师点拨
例1
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
例1
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.那么n边形的外角和等于多少度?
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
这位同学绕着五边形跑一圈,那么这位同学所转过的角度之和是多少度?
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
练一练
练习:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
练一练
练习:正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
108°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
练习.
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6。
练习:已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=___
A
B
C
D
E
1
2
解:∵
∠A+∠B+∠C=_______(
)
∠A=40°(
)
∴∠B+∠C=____
又∵∠B+
∠C+
∠1+
∠2=______
∴
∠1+∠2=___
180°
三角形的内角和等于180°
已知
140°
360°
220°
五、知识印证
(二)课堂小结
这节课我收获了什么?
(1)这节课我们主要学习了n边形的内角和公式:n边形的内角和=
(n-2)×180°
(2)从多边形的一个顶点出发可以引(n-3)条对角线,把多边形分成(n-2)个三角形.
作业布置
课本P24
:2题
P25
:4、5题
多边形的内角和
一、激发求知欲
1.三角形的内角和等于
度。
3.从四边形的一个顶点出发,可以引出
条对角线,这些对角线将多边形分割成
个三角形。
2.长方形的内角和等于
度。
1
2
180
360
返回
这些地砖是如何镶嵌的没有缝隙?
二、展示目标和任务
1.学习目标
(1)使学生了解多边形的内角和与外交和等概念。
(2)能通过不同方法探索多边形的内角和及外角和公式,并会应用它们进行有关计算。
2.学习任务
在探索多边形内角和时,学会如何把多边形转化成三角形
;并会利用外角与相邻内角之间的关系求多边形的外角和。
你能不能利用三角形的认识,求出这几个多边形的内角和?
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
以下图中从一个顶点出发可以引出几条对角线?
三、自主合作与交流
思考:n边形分成几个三角形如何表示?
n边形的内角和又如何表示?
A
B
C
D
B
A
C
E
D
B
F
E
D
C
A
180
°×2=
360
°
180
°
×3=
540
°
180
°
×4=
720
°
(4-2)
(5-2)
(6-2)
(n-2)
(n-2)
×
180
°
多边形的内角和
分成的三角形的个数
多边形的边数
1
…
180°
…
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
2
3
4
5
n-2
(n-2)×180
°
900
°
720
°
540
°
360
°
n边形每增加一条边,内角和的度数就增加180°
讨论:任意四边形的内角和等于多少度?除了上面这种分法,你还能找到几种方法?
A
B
C
D
F
E
A
B
C
D
A
B
C
D
F
F
分析一
:
180
°×2
=
360°
A
B
C
D
A
B
D
C
B
D
A
B
D
C
B
D
A
B
D
C
B
D
分析二
:
180
°
×3
-180
°=360°
A
B
C
D
A
D
E
E
A
B
C
D
E
A
B
E
A
D
E
C
E
D
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
想一想:这两种分割方法你又能不能求出多边形的内角和?
1、求八边形的内角和的度数.那七边形的内角和度数又为多少呢?
解:(8-2)×180°=1080°
(7-2)×180°=900°
答:八边形的内角和是1080°.
七边形的内角和是900°.
[提示:
n边形的内角和=
(n-2)×180°]
随堂练习
2、已知一个多边形的内角和等于1440°,求它的边数。
解:设这个多边形的边数为n,根据题意可得:
(n-2)×180°=1440°
解得:
n=10
答:这个多边形是十边形°
例1.如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
A
D
C
B
因为
∠A+∠B+
∠C+
∠D=360°
所以
∠B+
∠D
=360°-(
∠A+∠C
)
=360°-
180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
解:如图所示,四边形ABCD中,
不妨设∠A+∠C=180°
四、成果展示,教师点拨
例1
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
例1
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和
结论:五边形的外角和等于360°
-(5-2)
×
180°
=360
°
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-5边形内角和
=5×180°
探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.那么n边形的外角和等于多少度?
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2)
×
180°
=360
°
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180
°
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
这位同学绕着五边形跑一圈,那么这位同学所转过的角度之和是多少度?
由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。
即:多边形的外角和等于360?
练一练
练习:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。
12
n×30°=360°
n=12
n边形外角和=360
°
练一练
练习:正五边形的每一个外角等于____,每一个内角等于_____。
5X=360°
X=72°
108°
72°
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
所以每一个内角度数为108
°
练习.
已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:
设多边形的边数为n
∵它的内角和等于
(n-2)?180°,
多边形外角和等于360?,
∴
(n-2)?180°=2×
360?。
解得:
n=6
∴这个多边形的边数为6。
练习:已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=___
A
B
C
D
E
1
2
解:∵
∠A+∠B+∠C=_______(
)
∠A=40°(
)
∴∠B+∠C=____
又∵∠B+
∠C+
∠1+
∠2=______
∴
∠1+∠2=___
180°
三角形的内角和等于180°
已知
140°
360°
220°
五、知识印证
(二)课堂小结
这节课我收获了什么?
(1)这节课我们主要学习了n边形的内角和公式:n边形的内角和=
(n-2)×180°
(2)从多边形的一个顶点出发可以引(n-3)条对角线,把多边形分成(n-2)个三角形.
作业布置
课本P24
:2题
P25
:4、5题
