人教版八年级数学上册课件:12.1 全等三角形(共32张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:12.1 全等三角形(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-14 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
第十二章
全等三角形
12.1
全等三角形
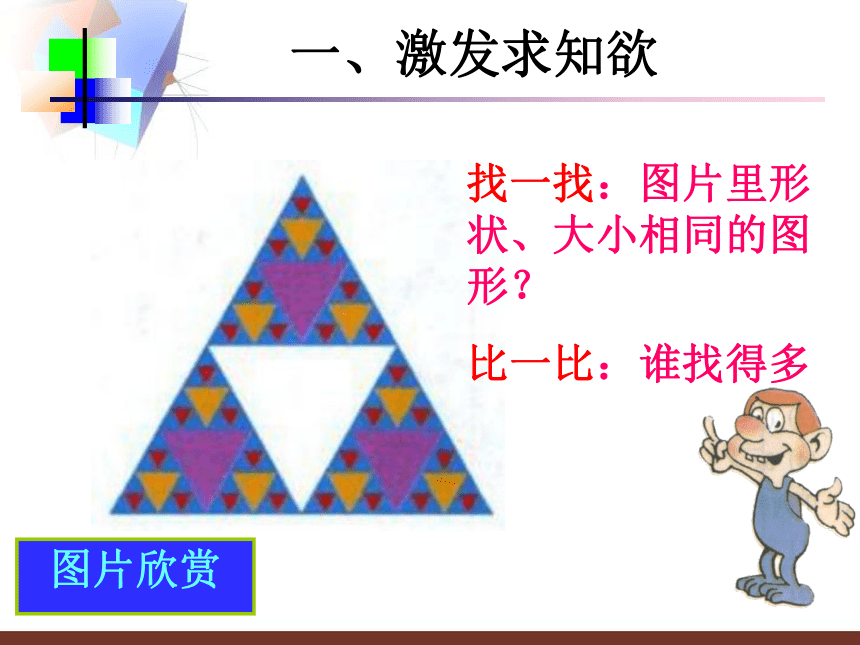
图片欣赏
找一找:图片里形状、大小相同的图形?
比一比:谁找得多
一、激发求知欲
图片欣赏
二、展示目标和任务
1.学习目标
(1)了解全等形、全等三角形及全等三角形的对应元素;掌握全等三角形的性质,能用符号正确地表示两个三角形全等;熟练找出两个全等三角形的对应角、对应边。
(2)通过全等三角形角有关概念的学习,提高对数学概念的辨析能力;通过找出全等三角形的对应元素,培养识图能力。
2.学习任务
学会找全等三角形的对应边、对应角,并会利用全等三角形的性质进行解题。
1.图
片
欣
赏
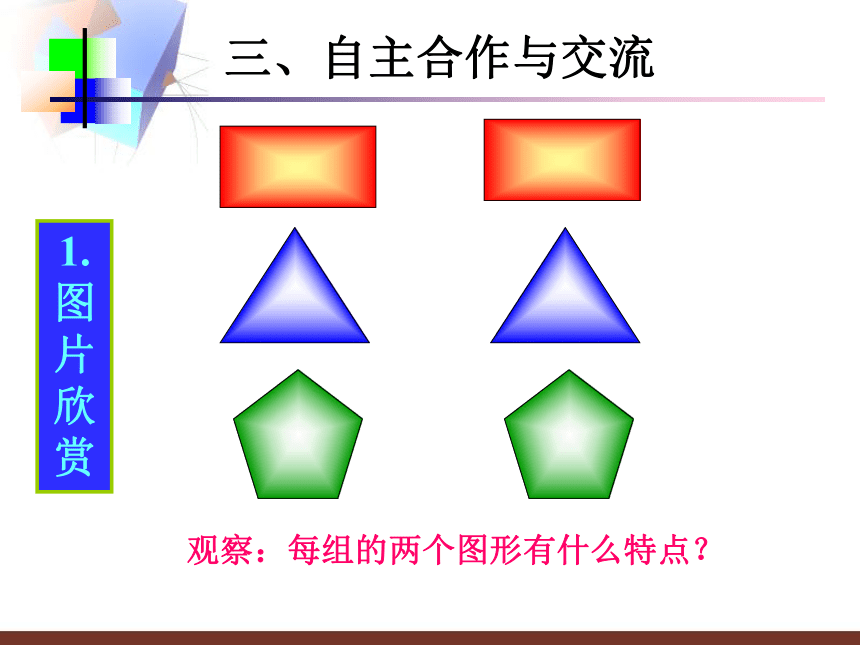
观察:每组的两个图形有什么特点?
三、自主合作与交流
观察图后讨论问题:
1、观察以上图案,找出形状与大小相同的图片。
2、你能再举出生活中的一些实际例子吗?
观察讨论
2.生活再现
两张纸重合
后
剪纸,得到的两个图形
大
小、形状相同。
生活再现
一张底片洗出的照片,得到的两个图形
大
小、形状相同。
生活再现
电脑复制的图形
大
小、形状相同。
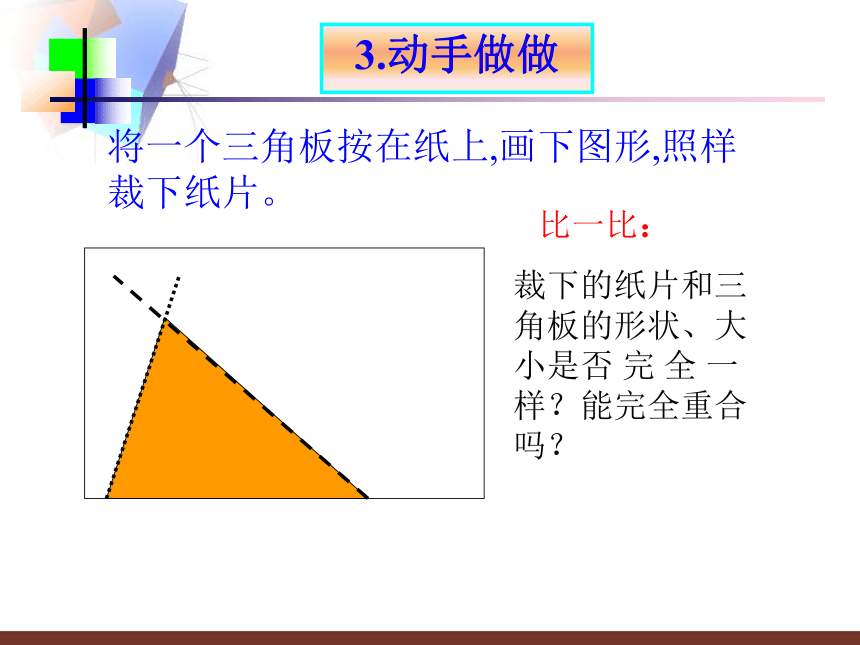
3.动手做做
将一个三角板按在纸上,画下图形,照样裁下纸片。
比一比:
裁下的纸片和三角板的形状、大小是否
完
全
一样?能完全重合吗?
形状、大小相同的图形放在一起能够完全重
合,能够完全重合的两个图形叫做全等形;
概念引入
能够完全重合的两个三角形叫做全等三角形。
“全等”用符号“≌”来表示,读作“全等于”
例:?ABC≌?DEF,读作?ABC全等于?DEF
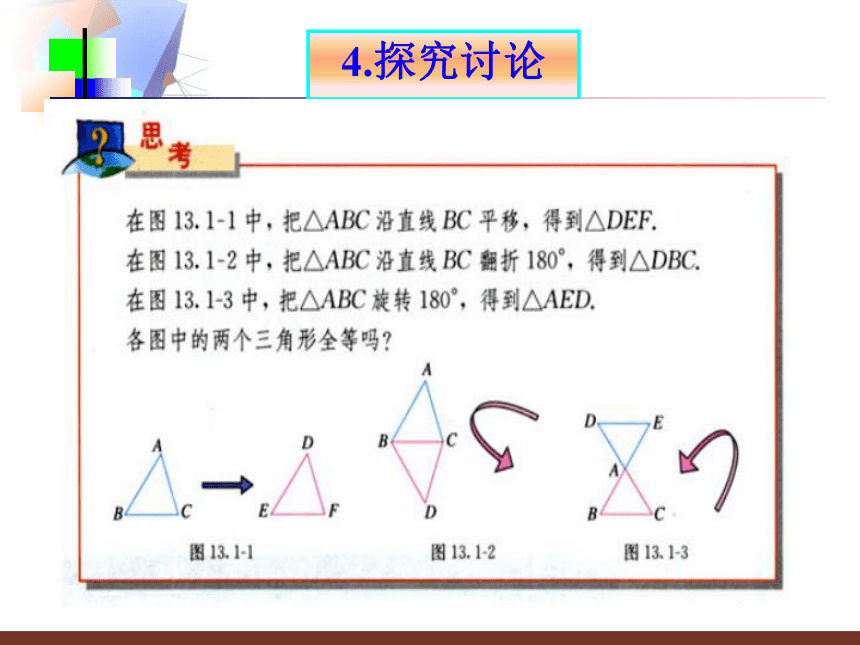
4.探究讨论
探究讨论
1、把?ABC沿直线BC平移,得到?DEF
F
A
E
D
C
B
平移
B
C
A
A
E
B
F
C
D
A
翻折
2、把?ABC沿直线BC翻折1800,得到?DEF
B
C
A
旋转
F
E
(D)
3、把?ABC沿点A旋转1800,得到?DEF
探究讨论
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变。
结论:平移,翻折,旋转前后的图形__。
形状
大小
全等
5.引入新知
F
E
D
B
C
A
互相重合的顶点叫做对应顶点
互相重合的边叫做对应边
互相重合的角叫做对应角
C
F
A
D
B
E
AB与DE
AC与DF
BC与EF
∠A与∠D
∠C与∠F
∠B与∠E
注意:两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
A
C
B
F
E
D
能否记作?ABC≌?DEF?
应该记作?ABC≌
?DFE
不能,原因:A与D、B与F、C与E对应。
感受新知
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
将剪得的两个三角形,按右图的位置
摆一摆,并指出他
们的对应顶点、对
应边、对应角。
引入新知
引入新知
(1)怎样的两条线段叫对应边?
(2)互相重合的两条线段的大小情况怎样?
全等三角形的对应边相等
同理,全等三角形能够互相重合的两角是对应角,而能互相重合的两角大小是相等的。
全等三角形的对应角相等
全等三角形的性质
如图:
∵
△ABC≌△DEF
全等三角形的性质:
对应边相等,对应角相等
∴A
B=D
E,A
C=D
F,BC=
E
F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
随
堂
练
习
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共顶点
公共角
公共边
四、成果展示,教师点拨
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
寻找对应边、对应角有什么规律?
寻找对应元素的规律:
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边也是对应边;
(5)两个全等三角形最大的角是对应角,最小的角也是对应角;
A
B
C
E
D
例题讲解:
如图,△ABE≌△ACD,AB与AC,
AD与AE是对应边,已知:
∠A=430,∠B=300,
求∠ADE的大小。
四、成果展示,教师点拨
1、全等用符号
表示,读作:
。
2、若△
BCE
≌
△
CBF,则∠CBE=
,
∠BEC=
,BE=
,
CE=
.
3、判断题
1)全等三角形的对应边相等,对应角相等。(
)
2)全等三角形的周长相等,面积也相等。
(
)
3)面积相等的三角形是全等三角形。
(
)
4)周长相等的三角形是全等三角形。
(
)
≌
全等于
∠BCF
CF
BF
∠CFB
√
√
X
X
五、知识印证
(一)练习
4.如图,
△ABD
≌
△EBC
D
A
B
C
E
(2)如果AB=3cm,BC=5cm,
求BE、BD及DE的长.
故DE=BD-BE=5-3=2cm
解:∵△ABD
≌
△EBC(已知)
∴AB=EB,BC=BD
∵AB=3cm,BC=5cm
∴BE=3cm,BD=5cm
(1)请找出对应边和对应角。
(全等三角形的对应边相等)
AB
EB、BC
BD、AD
EC,
∠A ∠BEC、∠D ∠C、∠ABD ∠EBC
=
与
与
与
与
与
与
=
=
=
=
=
(3)
如果AB=3cm,DE=2cm,
求BC的长.
A
B
C
D
E
∴BE=3cm
解:∵△ABD
≌
△EBC
∴AB=BE,BC=BD
∵AB=3cm
∴BC=BD=DE+BE
=2+3=5cm
5.如右图,已知△ABD≌△ACE,
且∠C=45°,AC
=
8,AE
=
5,则
∠B
=
,
DC
=
.
A
E
B
C
D
8
5
5
45°
3
(二)小结
1.能够重合的两个图形叫做
。
全等形
其中:互相重合的顶点叫做___
互相重合的边叫做___
互相重合的角叫做___
2.
叫做全等三角形
3.“全等”用符号“
”表示,读作“
”
4.全等三角形的
和
相等
5.书写全等式时要求把对应字母放在对应的位置上
对应顶点
对应角
对应边
能够重合的两个三角形
≌
全等于
对应边
对应角
(三)作业
必做题:
课本33页习题12.1第1,2,3题;
选做题:
课本33页习题12.1第4题;
第十二章
全等三角形
12.1
全等三角形
图片欣赏
找一找:图片里形状、大小相同的图形?
比一比:谁找得多
一、激发求知欲
图片欣赏
二、展示目标和任务
1.学习目标
(1)了解全等形、全等三角形及全等三角形的对应元素;掌握全等三角形的性质,能用符号正确地表示两个三角形全等;熟练找出两个全等三角形的对应角、对应边。
(2)通过全等三角形角有关概念的学习,提高对数学概念的辨析能力;通过找出全等三角形的对应元素,培养识图能力。
2.学习任务
学会找全等三角形的对应边、对应角,并会利用全等三角形的性质进行解题。
1.图
片
欣
赏
观察:每组的两个图形有什么特点?
三、自主合作与交流
观察图后讨论问题:
1、观察以上图案,找出形状与大小相同的图片。
2、你能再举出生活中的一些实际例子吗?
观察讨论
2.生活再现
两张纸重合
后
剪纸,得到的两个图形
大
小、形状相同。
生活再现
一张底片洗出的照片,得到的两个图形
大
小、形状相同。
生活再现
电脑复制的图形
大
小、形状相同。
3.动手做做
将一个三角板按在纸上,画下图形,照样裁下纸片。
比一比:
裁下的纸片和三角板的形状、大小是否
完
全
一样?能完全重合吗?
形状、大小相同的图形放在一起能够完全重
合,能够完全重合的两个图形叫做全等形;
概念引入
能够完全重合的两个三角形叫做全等三角形。
“全等”用符号“≌”来表示,读作“全等于”
例:?ABC≌?DEF,读作?ABC全等于?DEF
4.探究讨论
探究讨论
1、把?ABC沿直线BC平移,得到?DEF
F
A
E
D
C
B
平移
B
C
A
A
E
B
F
C
D
A
翻折
2、把?ABC沿直线BC翻折1800,得到?DEF
B
C
A
旋转
F
E
(D)
3、把?ABC沿点A旋转1800,得到?DEF
探究讨论
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变。
结论:平移,翻折,旋转前后的图形__。
形状
大小
全等
5.引入新知
F
E
D
B
C
A
互相重合的顶点叫做对应顶点
互相重合的边叫做对应边
互相重合的角叫做对应角
C
F
A
D
B
E
AB与DE
AC与DF
BC与EF
∠A与∠D
∠C与∠F
∠B与∠E
注意:两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
A
C
B
F
E
D
能否记作?ABC≌?DEF?
应该记作?ABC≌
?DFE
不能,原因:A与D、B与F、C与E对应。
感受新知
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
将剪得的两个三角形,按右图的位置
摆一摆,并指出他
们的对应顶点、对
应边、对应角。
引入新知
引入新知
(1)怎样的两条线段叫对应边?
(2)互相重合的两条线段的大小情况怎样?
全等三角形的对应边相等
同理,全等三角形能够互相重合的两角是对应角,而能互相重合的两角大小是相等的。
全等三角形的对应角相等
全等三角形的性质
如图:
∵
△ABC≌△DEF
全等三角形的性质:
对应边相等,对应角相等
∴A
B=D
E,A
C=D
F,BC=
E
F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
随
堂
练
习
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共顶点
公共角
公共边
四、成果展示,教师点拨
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
寻找对应边、对应角有什么规律?
寻找对应元素的规律:
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,最小的边也是对应边;
(5)两个全等三角形最大的角是对应角,最小的角也是对应角;
A
B
C
E
D
例题讲解:
如图,△ABE≌△ACD,AB与AC,
AD与AE是对应边,已知:
∠A=430,∠B=300,
求∠ADE的大小。
四、成果展示,教师点拨
1、全等用符号
表示,读作:
。
2、若△
BCE
≌
△
CBF,则∠CBE=
,
∠BEC=
,BE=
,
CE=
.
3、判断题
1)全等三角形的对应边相等,对应角相等。(
)
2)全等三角形的周长相等,面积也相等。
(
)
3)面积相等的三角形是全等三角形。
(
)
4)周长相等的三角形是全等三角形。
(
)
≌
全等于
∠BCF
CF
BF
∠CFB
√
√
X
X
五、知识印证
(一)练习
4.如图,
△ABD
≌
△EBC
D
A
B
C
E
(2)如果AB=3cm,BC=5cm,
求BE、BD及DE的长.
故DE=BD-BE=5-3=2cm
解:∵△ABD
≌
△EBC(已知)
∴AB=EB,BC=BD
∵AB=3cm,BC=5cm
∴BE=3cm,BD=5cm
(1)请找出对应边和对应角。
(全等三角形的对应边相等)
AB
EB、BC
BD、AD
EC,
∠A ∠BEC、∠D ∠C、∠ABD ∠EBC
=
与
与
与
与
与
与
=
=
=
=
=
(3)
如果AB=3cm,DE=2cm,
求BC的长.
A
B
C
D
E
∴BE=3cm
解:∵△ABD
≌
△EBC
∴AB=BE,BC=BD
∵AB=3cm
∴BC=BD=DE+BE
=2+3=5cm
5.如右图,已知△ABD≌△ACE,
且∠C=45°,AC
=
8,AE
=
5,则
∠B
=
,
DC
=
.
A
E
B
C
D
8
5
5
45°
3
(二)小结
1.能够重合的两个图形叫做
。
全等形
其中:互相重合的顶点叫做___
互相重合的边叫做___
互相重合的角叫做___
2.
叫做全等三角形
3.“全等”用符号“
”表示,读作“
”
4.全等三角形的
和
相等
5.书写全等式时要求把对应字母放在对应的位置上
对应顶点
对应角
对应边
能够重合的两个三角形
≌
全等于
对应边
对应角
(三)作业
必做题:
课本33页习题12.1第1,2,3题;
选做题:
课本33页习题12.1第4题;
