人教版七年级上册数学 1.2.4绝对值课件(共19张PPT)
文档属性
| 名称 | 人教版七年级上册数学 1.2.4绝对值课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 08:26:21 | ||
图片预览






文档简介
(共19张PPT)
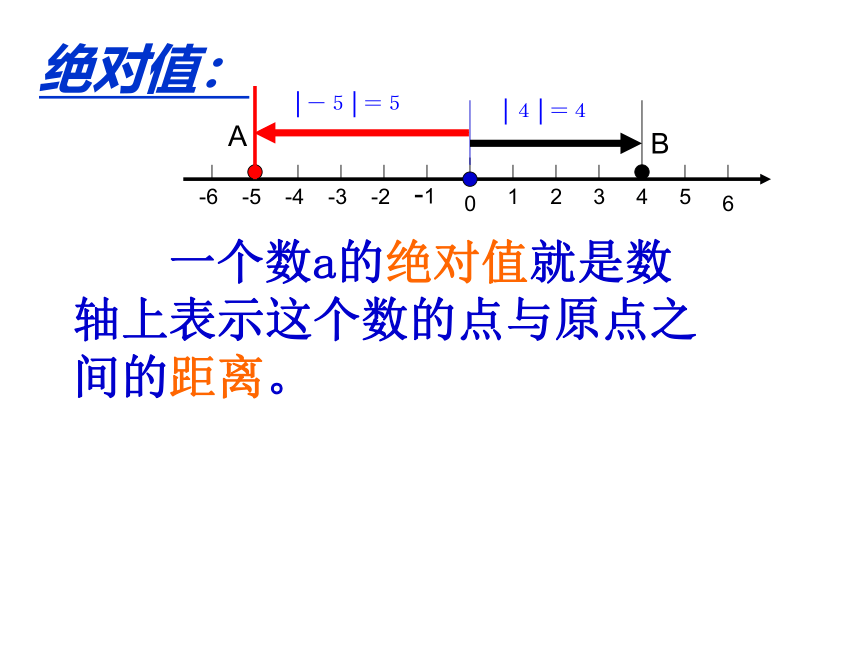
绝对值
0
6
一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
绝对值:
想一想:
互为相反数的两个数的绝对值有什么关系?
相等
例1
求下列各数的绝对值:
-21,
+4/9,
0,
-7.8
.
解:|-21|=21;|+4/9|=4/9;
|0|=0;
|-7.8|=7.8
.
议一议
一个数的绝对值与这个数有什么关系?
1,正数的绝对值是它本身;
如果a>0,那么|a|=a;
2,负数的绝对值是它的相反数;
如果a<0,那么|a|=-a;
3,0的绝对值是0.
如果a=0,那么|a|=0
做一做
(
1
)在数轴上表示下列各数,并比较它们的大小;
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小;
(
3
)你发现了什么?
解:(1)
-
5
<
-
3
<-
1.5
<
-
1
(2)|
-1.5
|
=
1.5
;
|
-
3
|
=
3;
|
-1
|
=
1
;
|
-
5
|
=
5.
(3)由以上知:两个负数比较大小,绝对值大的反而小。
1
<
1.5
<3
<5
解法一(利用绝对值比较两个负数的大小)
解:
(1)|
-1|
=
1,|
-5
|
=
5
,1﹤5,
所以
-
1>
-
5
例题
例2.
比较下列每组数的大小
(1)
-1和
–
5;
(2)-
和-
2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-
2.7在
-
的左边,所以-
2.7﹤-
因为-
5在
–1左边,所以
-
5﹤
-
1
试一试
1.字母
a
表示一个数,-a
表示什么?-a一定是负数吗?
解:字母
a
表示一个数,
-a
表示
a
的相反数,-a不一定是负数.
2.如果|
a
|
=
4,那么
a
等于__________.
4
或
-
4
3.一个数的绝对值是它本身,那么这个数一定是__________.
正数或零
4,3,2,1,0,-1,-2,-3,-4
4.绝对值小于5的整数有___个,分别是———
9
做一做
写出下列各数的绝对值:
解:
议一议
一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7
…………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3
…………
一个负数的绝对值是它的相反数
0的绝对值是0。即
|0|=0
而
原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
判断:
(1)一个数的绝对值是
2?,则这数是2
。
(2)|5|=|-5|。
(3)|-0.3|=|0.3|。
(4)|3|>0。
(5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。
(8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。
(10)互为相反数的两个数的绝对值相等。
想一想
1)
绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
2、已知有理数a在数轴上对应的点如图所示:
则|a|
=________
4、如果a
的相反数是-0.74,那么|a|
=______
3.
如果一个数的绝对值等于3.25
,则这个数是___
5.
如果|x-1|=2,则x=______.
课堂升华
a
0
(1)求绝对值不大于2的整数;
(2)已知x是整数,且2.5<|x|<7,
求x.
思考
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2,
3,(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
绝对值
0
6
一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
绝对值:
想一想:
互为相反数的两个数的绝对值有什么关系?
相等
例1
求下列各数的绝对值:
-21,
+4/9,
0,
-7.8
.
解:|-21|=21;|+4/9|=4/9;
|0|=0;
|-7.8|=7.8
.
议一议
一个数的绝对值与这个数有什么关系?
1,正数的绝对值是它本身;
如果a>0,那么|a|=a;
2,负数的绝对值是它的相反数;
如果a<0,那么|a|=-a;
3,0的绝对值是0.
如果a=0,那么|a|=0
做一做
(
1
)在数轴上表示下列各数,并比较它们的大小;
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小;
(
3
)你发现了什么?
解:(1)
-
5
<
-
3
<-
1.5
<
-
1
(2)|
-1.5
|
=
1.5
;
|
-
3
|
=
3;
|
-1
|
=
1
;
|
-
5
|
=
5.
(3)由以上知:两个负数比较大小,绝对值大的反而小。
1
<
1.5
<3
<5
解法一(利用绝对值比较两个负数的大小)
解:
(1)|
-1|
=
1,|
-5
|
=
5
,1﹤5,
所以
-
1>
-
5
例题
例2.
比较下列每组数的大小
(1)
-1和
–
5;
(2)-
和-
2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-
2.7在
-
的左边,所以-
2.7﹤-
因为-
5在
–1左边,所以
-
5﹤
-
1
试一试
1.字母
a
表示一个数,-a
表示什么?-a一定是负数吗?
解:字母
a
表示一个数,
-a
表示
a
的相反数,-a不一定是负数.
2.如果|
a
|
=
4,那么
a
等于__________.
4
或
-
4
3.一个数的绝对值是它本身,那么这个数一定是__________.
正数或零
4,3,2,1,0,-1,-2,-3,-4
4.绝对值小于5的整数有___个,分别是———
9
做一做
写出下列各数的绝对值:
解:
议一议
一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7
…………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3
…………
一个负数的绝对值是它的相反数
0的绝对值是0。即
|0|=0
而
原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
判断:
(1)一个数的绝对值是
2?,则这数是2
。
(2)|5|=|-5|。
(3)|-0.3|=|0.3|。
(4)|3|>0。
(5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。
(8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。
(10)互为相反数的两个数的绝对值相等。
想一想
1)
绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
2、已知有理数a在数轴上对应的点如图所示:
则|a|
=________
4、如果a
的相反数是-0.74,那么|a|
=______
3.
如果一个数的绝对值等于3.25
,则这个数是___
5.
如果|x-1|=2,则x=______.
课堂升华
a
0
(1)求绝对值不大于2的整数;
(2)已知x是整数,且2.5<|x|<7,
求x.
思考
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2,
3,(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
