人教版数学八年级上册11.2.1.1三角形的内角教案
文档属性
| 名称 | 人教版数学八年级上册11.2.1.1三角形的内角教案 |  | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 23:08:13 | ||
图片预览

文档简介
《§11.2.1
三角形的内角》教学设计
教学目标
1、知识技能:
(1)知道“三角形的内角和等于180°”,
(2)能运用三角形内角和定理解决一些简单的实际问题.
2、数学思考:
(1)通过测量、猜想、推理等数学活动,探索三角形的内角和,感受数学思考过程的条理性,发展合情推理能力和语言表达能力.
(2)理解三角形内角和的计算、验证,其本质就是想法把三个内角集中在一起转化为一个平角,其方法可以用拼合的方法,也可以用引平行线的方法.
3、解决问题:
通过小组学习等活动经历得出三角形的内角和等于180°
的过程,进一步提高学生应用所学知识解决问题的能力.
4、情感态度:
在观察、操作、推理、归纳等探索过程中,发展同学们的合情推理能力,逐步养成和获得数学说理的习惯与能力.
教学重难点
1、重点:三角形内角和定理.
2、难点:三角形内角和定理的推导、验证过程.
课前准备
三角板、三角形纸片若干.
教学过程
【活动1】创设情景,自然引入
∠1、∠2、∠3一个三角形的三个内角,平时,它们三兄弟非常团结。可是有一天,∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊!老弟。”∠1说,“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”
∠2很纳闷.
同学们,你们知道其中的道理吗?学了今天的知识以后,你们就知道它们三兄弟之间的关系了……
【活动2】学习新课
问题1
:
1、△ABC有几条边?
2、△ABC有哪几个内角?
问题2:
1、画一个三角形.
2、量出三角形中三个内角的度数,三个内角的和是多少度?
3、任意一个三角形的内角和都相同吗?它是多少度呢?
问题3:
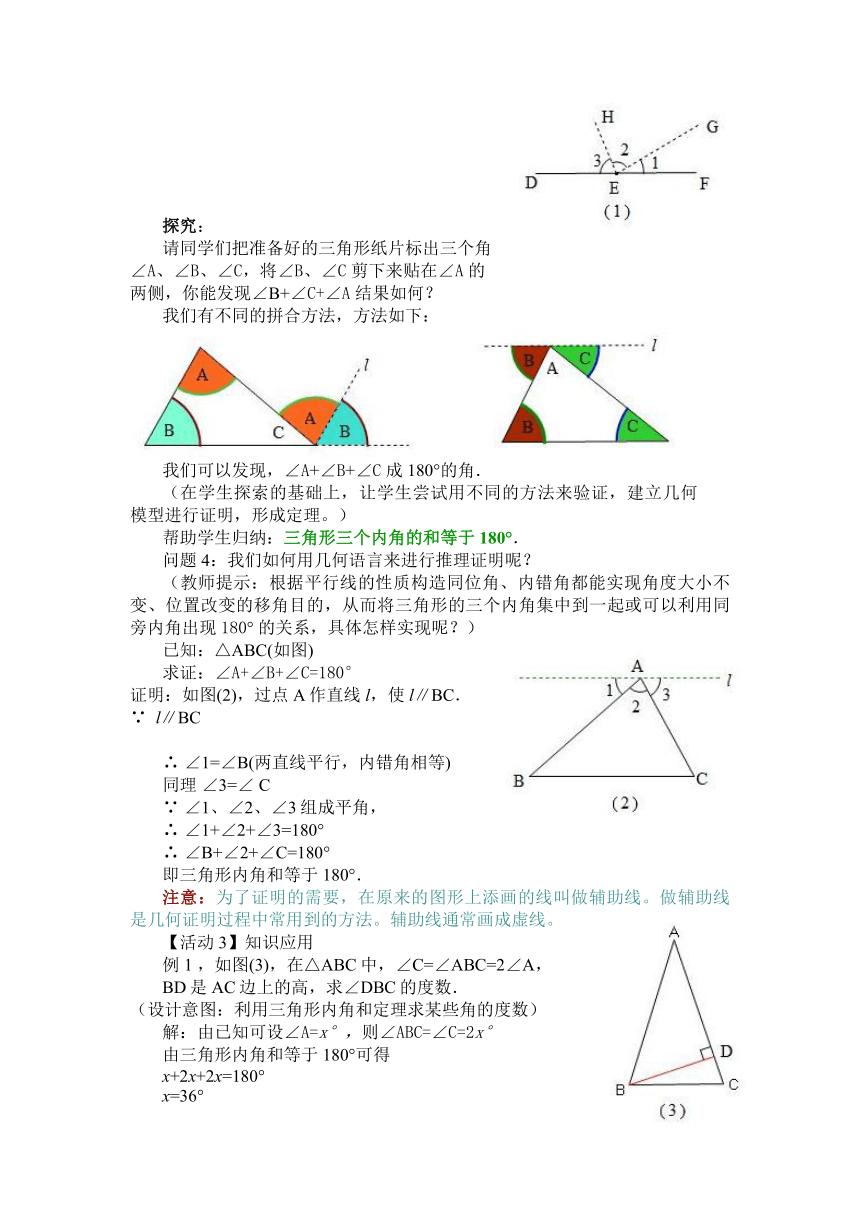
1、什么是平角?平角有多少度?
2、如图(1),已知∠1=30°,∠2=80°,求∠3的度数.
探究:
请同学们把准备好的三角形纸片标出三个角
∠A、∠B、∠C,将∠B、∠C剪下来贴在∠A的
两侧,你能发现∠B+∠C+∠A结果如何?
我们有不同的拼合方法,方法如下:
我们可以发现,∠A+∠B+∠C成180°的角.
(在学生探索的基础上,让学生尝试用不同的方法来验证,建立几何模型进行证明,形成定理。)
帮助学生归纳:三角形三个内角的和等于180°.
问题4:我们如何用几何语言来进行推理证明呢?
(教师提示:根据平行线的性质构造同位角、内错角都能实现角度大小不变、位置改变的移角目的,从而将三角形的三个内角集中到一起或可以利用同旁内角出现180°
的关系,具体怎样实现呢?)
已知:△ABC(如图)
求证:∠A+∠B+∠C=180°
证明:如图(2),过点A作直线l,使l∥BC.
∵
l∥BC
∴
∠1=∠B(两直线平行,内错角相等)
同理
∠3=∠
C
∵
∠1、∠2、∠3组成平角,
∴
∠1+∠2+∠3=180°
∴
∠B+∠2+∠C=180°
即三角形内角和等于180°.
注意:为了证明的需要,在原来的图形上添画的线叫做辅助线。做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
【活动3】知识应用
例1
,如图(3),在△ABC中,∠C=∠ABC=2∠A,
BD是AC边上的高,求∠DBC的度数.
(设计意图:利用三角形内角和定理求某些角的度数)
解:由已知可设∠A=x°,则∠ABC=∠C=2x°
由三角形内角和等于180°可得
x+2x+2x=180°
x=36°
∴
∠C=2x=36°×2=72°
∵
BD是AC边上的高
∴
∠BDC=90°
∴
∠DBC
=180°-∠BDC-∠C
=180°-90°-72°
=18°
答:∠DBC的度数是18°.
例2,如图(4),C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°
方向,从C岛看A,B两岛的视角∠ACB是多少度?
解法一:(师生共同讨论,解法见书上).
解法二:过C作AD的垂线,交直线AD于点M,交直线BE于点N(如图5).
∵
CM⊥AD
∴
∠AMC=90°
∵
AD∥BE
∴
∠BNC=180°-∠AMC=180°-90°=90°
在△ACM中,
∠ACM=180°-∠AMC-∠CAM=180°-90°-50°=40°
在△BCN中,
∠BCN
=180°-∠BNC-∠CBN=180°-90°-40°=50°
由平角的定义可得,
∠ACB=180°-∠ACM-∠BCN=180°-40°-50°=90°
解法三:过C作CF平行于AD(如图6).
∵
CF∥AD
∴
∠ACF=∠DAC=50°
∵
CF∥BE
∴
∠BCF=∠CBE=40°
∴
∠ACB=∠ACF+∠BCF=50°+40°=90°
答:从C岛看A,B两岛的视角∠ACB是90°.
【活动4】能力提升
1、下图中三角形被遮住的两个内角是什么角?试说明理由.
2、填空
(1)
在△ABC中,∠A=20°,∠B=80°,
则∠C=_______。
(2)
在△ABC中,∠C=90°,∠B=56°,
则∠A=_______。
(3)在△ABC中,
∠A=50°,∠A=2∠B,则∠C=_______。
(4)在△ABC中,∠A等于直角的一半,∠B等于直角的,则∠C=_______.
3、完成教材13页练习1、2题.
【活动5】回顾与小结
1、三角形内角和是多少度?
2、本节课我们共同探索了三角形内角和定理及推论的证明,基本思路是:把三个内角拼在一起,拼成一个平角.
3、能用几何语言描述三角形内角和的推理过程,熟练掌握三角形内角和定理,并能解简单问题.
必要作业:教材P16第3、4题.
板书设计:
教学反思:
1、本课设计符合学生的认知规律.先让学生动手操作以便使学生对三角形内角和有感性认识,然后再根据拼图说出结论成立的理由,由浅人深,循序渐进,学生易接受.
2、体现自主学习、合作交流的新课程理念.无论是例题还是习题的教学均采用“尝试—交流—讨论”的方式,充分发挥学生的主体性,教师起引导、点拨的作用.
三角形的内角》教学设计
教学目标
1、知识技能:
(1)知道“三角形的内角和等于180°”,
(2)能运用三角形内角和定理解决一些简单的实际问题.
2、数学思考:
(1)通过测量、猜想、推理等数学活动,探索三角形的内角和,感受数学思考过程的条理性,发展合情推理能力和语言表达能力.
(2)理解三角形内角和的计算、验证,其本质就是想法把三个内角集中在一起转化为一个平角,其方法可以用拼合的方法,也可以用引平行线的方法.
3、解决问题:
通过小组学习等活动经历得出三角形的内角和等于180°
的过程,进一步提高学生应用所学知识解决问题的能力.
4、情感态度:
在观察、操作、推理、归纳等探索过程中,发展同学们的合情推理能力,逐步养成和获得数学说理的习惯与能力.
教学重难点
1、重点:三角形内角和定理.
2、难点:三角形内角和定理的推导、验证过程.
课前准备
三角板、三角形纸片若干.
教学过程
【活动1】创设情景,自然引入
∠1、∠2、∠3一个三角形的三个内角,平时,它们三兄弟非常团结。可是有一天,∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊!老弟。”∠1说,“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”
∠2很纳闷.
同学们,你们知道其中的道理吗?学了今天的知识以后,你们就知道它们三兄弟之间的关系了……
【活动2】学习新课
问题1
:
1、△ABC有几条边?
2、△ABC有哪几个内角?
问题2:
1、画一个三角形.
2、量出三角形中三个内角的度数,三个内角的和是多少度?
3、任意一个三角形的内角和都相同吗?它是多少度呢?
问题3:
1、什么是平角?平角有多少度?
2、如图(1),已知∠1=30°,∠2=80°,求∠3的度数.
探究:
请同学们把准备好的三角形纸片标出三个角
∠A、∠B、∠C,将∠B、∠C剪下来贴在∠A的
两侧,你能发现∠B+∠C+∠A结果如何?
我们有不同的拼合方法,方法如下:
我们可以发现,∠A+∠B+∠C成180°的角.
(在学生探索的基础上,让学生尝试用不同的方法来验证,建立几何模型进行证明,形成定理。)
帮助学生归纳:三角形三个内角的和等于180°.
问题4:我们如何用几何语言来进行推理证明呢?
(教师提示:根据平行线的性质构造同位角、内错角都能实现角度大小不变、位置改变的移角目的,从而将三角形的三个内角集中到一起或可以利用同旁内角出现180°
的关系,具体怎样实现呢?)
已知:△ABC(如图)
求证:∠A+∠B+∠C=180°
证明:如图(2),过点A作直线l,使l∥BC.
∵
l∥BC
∴
∠1=∠B(两直线平行,内错角相等)
同理
∠3=∠
C
∵
∠1、∠2、∠3组成平角,
∴
∠1+∠2+∠3=180°
∴
∠B+∠2+∠C=180°
即三角形内角和等于180°.
注意:为了证明的需要,在原来的图形上添画的线叫做辅助线。做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
【活动3】知识应用
例1
,如图(3),在△ABC中,∠C=∠ABC=2∠A,
BD是AC边上的高,求∠DBC的度数.
(设计意图:利用三角形内角和定理求某些角的度数)
解:由已知可设∠A=x°,则∠ABC=∠C=2x°
由三角形内角和等于180°可得
x+2x+2x=180°
x=36°
∴
∠C=2x=36°×2=72°
∵
BD是AC边上的高
∴
∠BDC=90°
∴
∠DBC
=180°-∠BDC-∠C
=180°-90°-72°
=18°
答:∠DBC的度数是18°.
例2,如图(4),C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°
方向,从C岛看A,B两岛的视角∠ACB是多少度?
解法一:(师生共同讨论,解法见书上).
解法二:过C作AD的垂线,交直线AD于点M,交直线BE于点N(如图5).
∵
CM⊥AD
∴
∠AMC=90°
∵
AD∥BE
∴
∠BNC=180°-∠AMC=180°-90°=90°
在△ACM中,
∠ACM=180°-∠AMC-∠CAM=180°-90°-50°=40°
在△BCN中,
∠BCN
=180°-∠BNC-∠CBN=180°-90°-40°=50°
由平角的定义可得,
∠ACB=180°-∠ACM-∠BCN=180°-40°-50°=90°
解法三:过C作CF平行于AD(如图6).
∵
CF∥AD
∴
∠ACF=∠DAC=50°
∵
CF∥BE
∴
∠BCF=∠CBE=40°
∴
∠ACB=∠ACF+∠BCF=50°+40°=90°
答:从C岛看A,B两岛的视角∠ACB是90°.
【活动4】能力提升
1、下图中三角形被遮住的两个内角是什么角?试说明理由.
2、填空
(1)
在△ABC中,∠A=20°,∠B=80°,
则∠C=_______。
(2)
在△ABC中,∠C=90°,∠B=56°,
则∠A=_______。
(3)在△ABC中,
∠A=50°,∠A=2∠B,则∠C=_______。
(4)在△ABC中,∠A等于直角的一半,∠B等于直角的,则∠C=_______.
3、完成教材13页练习1、2题.
【活动5】回顾与小结
1、三角形内角和是多少度?
2、本节课我们共同探索了三角形内角和定理及推论的证明,基本思路是:把三个内角拼在一起,拼成一个平角.
3、能用几何语言描述三角形内角和的推理过程,熟练掌握三角形内角和定理,并能解简单问题.
必要作业:教材P16第3、4题.
板书设计:
教学反思:
1、本课设计符合学生的认知规律.先让学生动手操作以便使学生对三角形内角和有感性认识,然后再根据拼图说出结论成立的理由,由浅人深,循序渐进,学生易接受.
2、体现自主学习、合作交流的新课程理念.无论是例题还是习题的教学均采用“尝试—交流—讨论”的方式,充分发挥学生的主体性,教师起引导、点拨的作用.
