人教版八年级数学上册 12.1 全等三角形课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册 12.1 全等三角形课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
第十二章
全等三角形
12.1
全等三角形
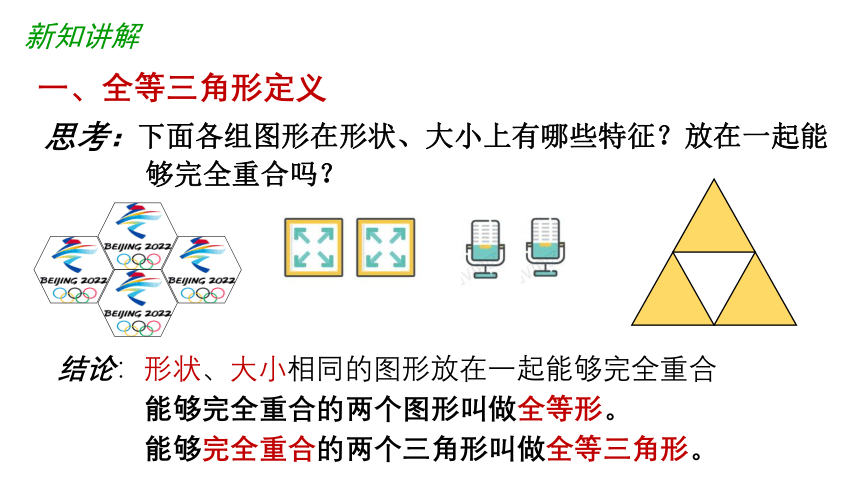
新知讲解
思考:下面各组图形在形状、大小上有哪些特征?放在一起能
够完全重合吗?
一、全等三角形定义
结论:形状、大小相同的图形放在一起能够完全重合
能够完全重合的两个图形叫做全等形。
能够完全重合的两个三角形叫做全等三角形。
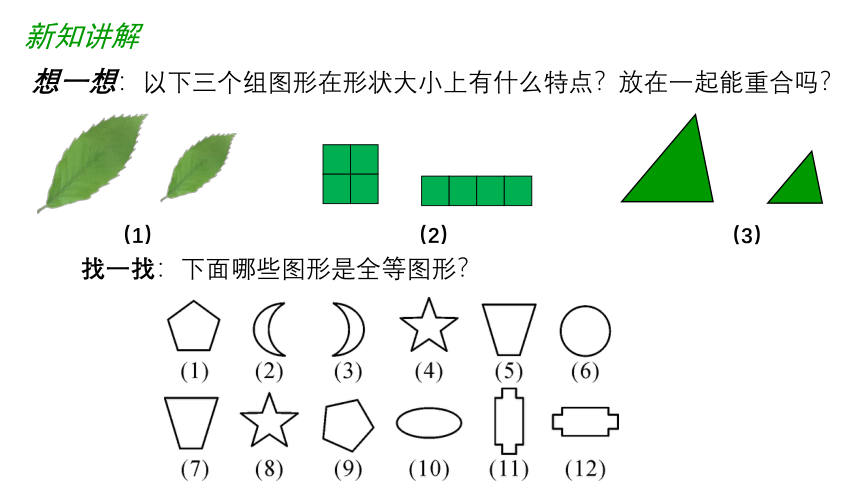
新知讲解
(1)
(2)
想一想:以下三个组图形在形状大小上有什么特点?放在一起能重合吗?
(3)
找一找:下面哪些图形是全等图形?
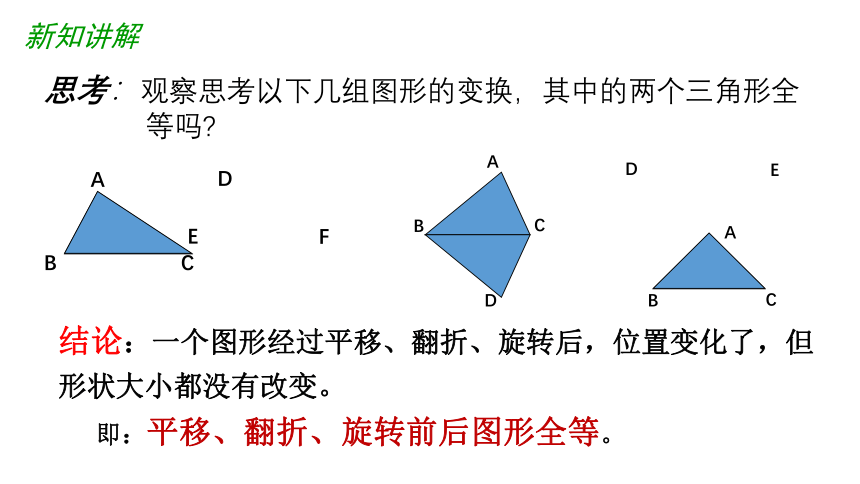
新知讲解
思考:观察思考以下几组图形的变换,其中的两个三角形全
等吗?
A
E
D
F
C
B
A
B
D
C
A
B
E
D
C
结论:一个图形经过平移、翻折、旋转后,位置变化了,但形状大小都没有改变。
即:平移、翻折、旋转前后图形全等。
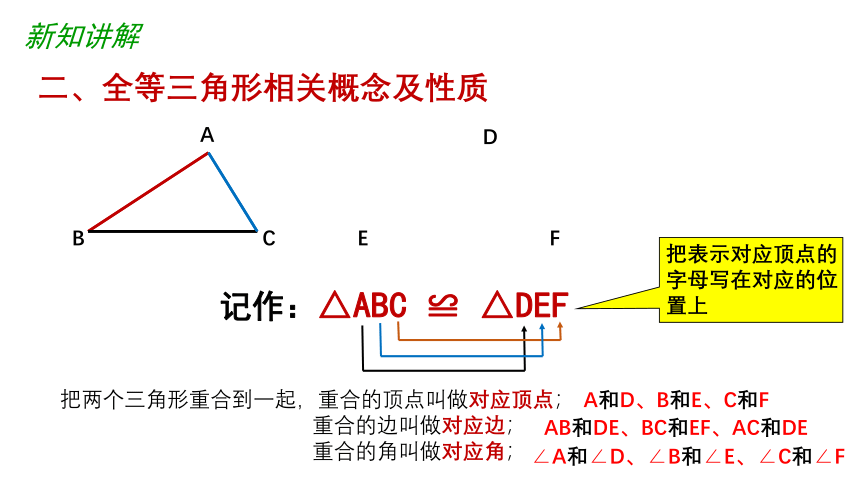
新知讲解
二、全等三角形相关概念及性质
F
E
D
C
B
A
把两个三角形重合到一起,重合的顶点叫做对应顶点;
重合的边叫做对应边;
重合的角叫做对应角;
记作:△ABC
≌
△DEF
A和D、B和E、C和F
AB和DE、BC和EF、AC和DE
∠A和∠D、∠B和∠E、∠C和∠F
把表示对应顶点的字母写在对应的位置上
新知讲解
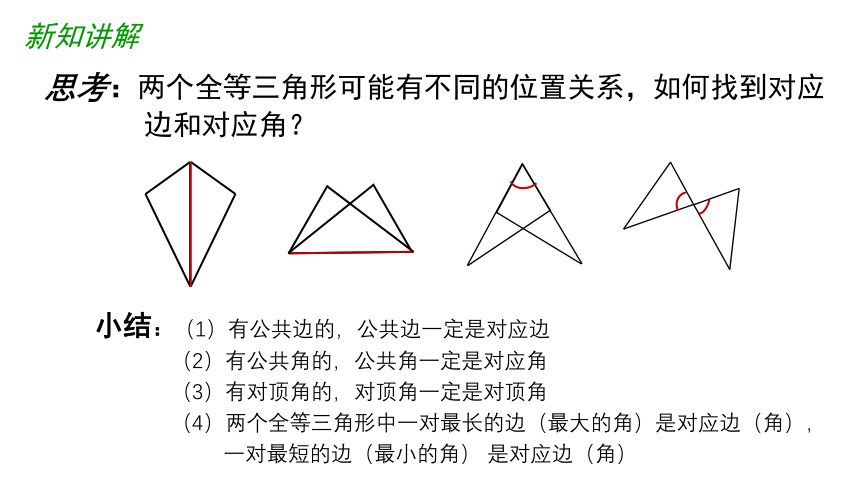
思考:两个全等三角形可能有不同的位置关系,如何找到对应
边和对应角?
小结:(1)有公共边的,公共边一定是对应边
(2)有公共角的,公共角一定是对应角
(3)有对顶角的,对顶角一定是对顶角
(4)两个全等三角形中一对最长的边(最大的角)是对应边(角),
一对最短的边(最小的角)
是对应边(角)
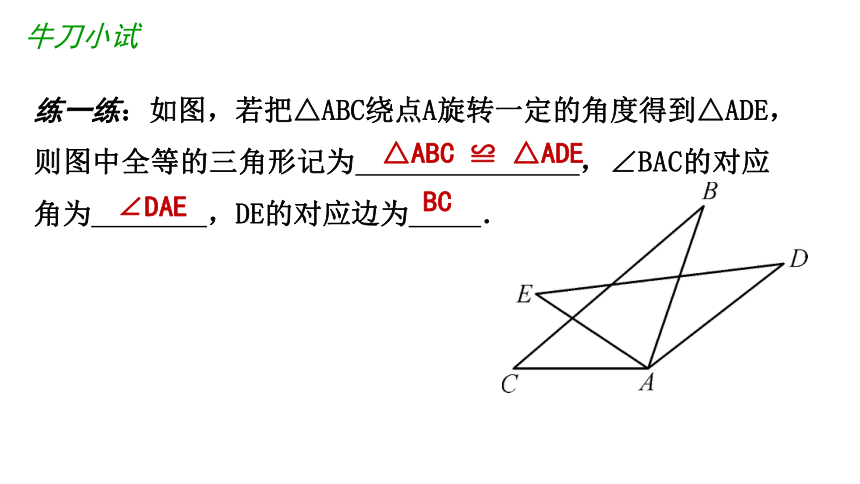
牛刀小试
练一练:如图,若把△ABC绕点A旋转一定的角度得到△ADE,则图中全等的三角形记为
,∠BAC的对应角为
,DE的对应边为
.
△ABC
≌
△ADE
∠DAE
BC
C
B
A
F
E
D
思考:如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
新知讲解
全等三角形有这样的性质:
全等三角形的对应边相等
全等三角形的对应角相等。
应用:
∵△ABC
≌
△DEF
∴∠BAC=∠EDF,∠ABC=∠DEF,
∠ACB=∠DFE
AB=DE,AC=DF,BC=EF
例题讲解
例1、如图,△ABC≌△DEF,∠A=70°,∠B=50°,
BF=4,EF=7,求∠DEF的度数和CF的长
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例题讲解
例2、如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,
EG和NH;
对应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
新知讲解
(2)求线段NM及HG的长度;
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
你还能得出其他结论吗?
(3)观察图形中对应线段的数量或位置关系,试提出一个正确
的结论并证明.
牛刀小试
1.下列叙述中错误的是(
)
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
牛刀小试
2、如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=
.
3、如图,把△ABC沿直线BA翻折至△ABD,那么△ABC和△ABD
全等三角形(填“是”或“不是”).若CB=5,则DB=
;若△ABC的面积为10,则△ABD的面积为多少?
牛刀小试
4、如图所示,将△ABC沿AC翻折,点B与点E
重合,则图中全等的三角形有(
)
A.1对
B.2对
C.3对
D.4对
牛刀小试
5、如图所示,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
牛刀小试
6、如图,△ACE≌△DBF,AC=6,BC=4.
(1)求证:AE∥DF;
(2)求AD的长度。
牛刀小试
7、如图所示,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗?
(2)请你猜想△ABD满足什么条件时,BD∥CE?
牛刀小试
第十二章
全等三角形
12.1
全等三角形
新知讲解
思考:下面各组图形在形状、大小上有哪些特征?放在一起能
够完全重合吗?
一、全等三角形定义
结论:形状、大小相同的图形放在一起能够完全重合
能够完全重合的两个图形叫做全等形。
能够完全重合的两个三角形叫做全等三角形。
新知讲解
(1)
(2)
想一想:以下三个组图形在形状大小上有什么特点?放在一起能重合吗?
(3)
找一找:下面哪些图形是全等图形?
新知讲解
思考:观察思考以下几组图形的变换,其中的两个三角形全
等吗?
A
E
D
F
C
B
A
B
D
C
A
B
E
D
C
结论:一个图形经过平移、翻折、旋转后,位置变化了,但形状大小都没有改变。
即:平移、翻折、旋转前后图形全等。
新知讲解
二、全等三角形相关概念及性质
F
E
D
C
B
A
把两个三角形重合到一起,重合的顶点叫做对应顶点;
重合的边叫做对应边;
重合的角叫做对应角;
记作:△ABC
≌
△DEF
A和D、B和E、C和F
AB和DE、BC和EF、AC和DE
∠A和∠D、∠B和∠E、∠C和∠F
把表示对应顶点的字母写在对应的位置上
新知讲解
思考:两个全等三角形可能有不同的位置关系,如何找到对应
边和对应角?
小结:(1)有公共边的,公共边一定是对应边
(2)有公共角的,公共角一定是对应角
(3)有对顶角的,对顶角一定是对顶角
(4)两个全等三角形中一对最长的边(最大的角)是对应边(角),
一对最短的边(最小的角)
是对应边(角)
牛刀小试
练一练:如图,若把△ABC绕点A旋转一定的角度得到△ADE,则图中全等的三角形记为
,∠BAC的对应角为
,DE的对应边为
.
△ABC
≌
△ADE
∠DAE
BC
C
B
A
F
E
D
思考:如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
新知讲解
全等三角形有这样的性质:
全等三角形的对应边相等
全等三角形的对应角相等。
应用:
∵△ABC
≌
△DEF
∴∠BAC=∠EDF,∠ABC=∠DEF,
∠ACB=∠DFE
AB=DE,AC=DF,BC=EF
例题讲解
例1、如图,△ABC≌△DEF,∠A=70°,∠B=50°,
BF=4,EF=7,求∠DEF的度数和CF的长
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例题讲解
例2、如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,
EG和NH;
对应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
新知讲解
(2)求线段NM及HG的长度;
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,
EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
你还能得出其他结论吗?
(3)观察图形中对应线段的数量或位置关系,试提出一个正确
的结论并证明.
牛刀小试
1.下列叙述中错误的是(
)
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
牛刀小试
2、如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=
.
3、如图,把△ABC沿直线BA翻折至△ABD,那么△ABC和△ABD
全等三角形(填“是”或“不是”).若CB=5,则DB=
;若△ABC的面积为10,则△ABD的面积为多少?
牛刀小试
4、如图所示,将△ABC沿AC翻折,点B与点E
重合,则图中全等的三角形有(
)
A.1对
B.2对
C.3对
D.4对
牛刀小试
5、如图所示,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系?为什么?
牛刀小试
6、如图,△ACE≌△DBF,AC=6,BC=4.
(1)求证:AE∥DF;
(2)求AD的长度。
牛刀小试
7、如图所示,A,D,E三点在同一直线上,△BAD≌△ACE.
(1)你能说明BD,DE,CE之间的数量关系吗?
(2)请你猜想△ABD满足什么条件时,BD∥CE?
牛刀小试
