人教版八年级上册数学讲义:12.1全等三角形(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册数学讲义:12.1全等三角形(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 12:17:13 | ||
图片预览

文档简介
课题:全等三角形
中考要求
1.了解全等三角形的有关概念。
2.探索两个三角形全等的条件。
3.掌握两个三角形全等的条件。
4.解决全等三角形与其他知识的综合问题。
知识梳理
3.角平分线的性质:到角平分线上的点到角的两边的距离相等.
4.角平分线性质的逆定理:到角两边距离相等的点在角的平分线上.
典例解析
例1.阅读下题:如图,P是△ABC中BC边上一点,E是AP上的一点,若EB=EC,∠1=∠2,
求证:AP⊥BC。
证明:在△ABE和△ACE中,EB=EC,AE=AE,∠1=∠2
∴△ABE≌△ACE(第一步)
∴AB=AC,∠3=∠4(第二步)
∴AP⊥BC(等腰三角形三线合一)
上面的证明过程是否正确?若正确,请写出每一步的推理依据;若不正确,
请指出关键错在哪一步,并写出你认为正确的证明过程。
例2.已知:AB、CD相交于点O,AC∥DB,OC=OD,E、F为AB上两点,且AE=BF.求证:CE=DF
例3.如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD。
分析:采用截长补短法,延长AC至
E,使AE=AB,连结DE;也可在AB上
截取AE=AC,
再证明EB=CD(证明略)。
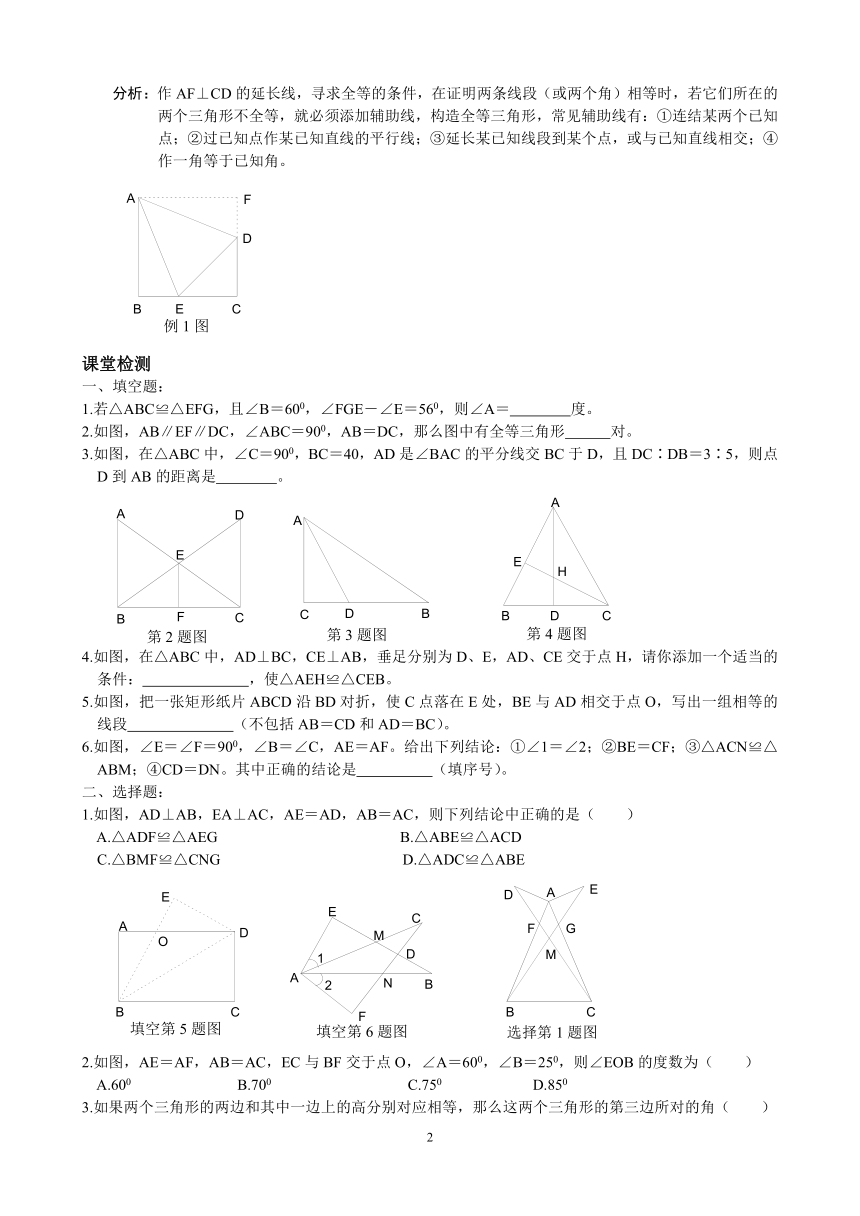
例4.如图,已知AB⊥BC,DC⊥BC,E在BC上,AE=AD,AB=BC。求证:CE=CD。
分析:作AF⊥CD的延长线,寻求全等的条件,在证明两条线段(或两个角)相等时,若它们所在的两个三角形不全等,就必须添加辅助线,构造全等三角形,常见辅助线有:①连结某两个已知点;②过已知点作某已知直线的平行线;③延长某已知线段到某个点,或与已知直线相交;④作一角等于已知角。
课堂检测
一、填空题:
1.若△ABC≌△EFG,且∠B=600,∠FGE-∠E=560,则∠A=
度。
2.如图,AB∥EF∥DC,∠ABC=900,AB=DC,那么图中有全等三角形
对。
3.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是
。
4.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:
,使△AEH≌△CEB。
5.如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段
(不包括AB=CD和AD=BC)。
6.如图,∠E=∠F=900,∠B=∠C,AE=AF。给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论是
(填序号)。
二、选择题:
1.如图,AD⊥AB,EA⊥AC,AE=AD,AB=AC,则下列结论中正确的是(
)
A.△ADF≌△AEG
B.△ABE≌△ACD
C.△BMF≌△CNG
D.△ADC≌△ABE
2.如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为(
)
A.600
B.700
C.750
D.850
3.如果两个三角形的两边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角(
)
A.相等
B.不相等
C.互余
D.互补或相等
4.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=,PC=,AB=,AC=,则与的大小关系是(
)
A.>
B.<
C.=
D.无法确定
课后测评
1.如图,已知∠MON的边OM上有两点A、B,边ON上有两点C、D,且AB=CD,P为∠MON的平分线上一点。问:
(1)△ABP与△PCD是否全等?请说明理由。
(2)△ABP与△PCD的面积是否相等?请说明理由。
2.已知:中,BAC=90,AD是BC边上的高,BF平分ABC,交AD于E。
求证:AEF是等腰三角形
3.已知:如图AB=CD,AC和BD的垂直平分线相交于O点。
求证:ABO=CDO
4.已知:如图ABC中,BC边中垂线DE交BAC的平分线于D,DM⊥AB于M,DN⊥AC于N。
求证BM=CN
中考链接
1.如图所示:若△ABC≌△DEF∠A=50度,∠B=30度,则∠E等于(
)
A.30度??
B.50度
C.60度???
D.100度
2.如图所示:在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是(
)
A.15度??
B.20度
C.25度???
D.30
3.如图所示:点P是∠BAC的平分线AD上一点,
PE⊥AC于点E,
已知PE=3,
则点P到AB的距离是(
)
A.
3
B
。
4
C
。
5
D。
6
4.如图所示:在△ABC中,
已知∠ABC和∠ACB的平分线相交于F,
过点F作DE∥BC,交AB于点D,
交AC于点E,
若BD+CE=9,
则线段DE的长为(
)
A.9
B.8
C.7
D.6
5.如图所示:AB=AC,
EB=EC
,
AE的延长线交BC于D,那么图中的全等三角形共有
对
6.已知:如图,△ABC和△DBC的顶点A和D在BC的同旁,AB=DC,AC=DB,AC和DB相交于点O.求证:
∠A=∠D
全等三角形参考答案
课堂检测
一、填空题:
1、32;2、3;3、15;4、AH=BC或EA=EC或EH=EB等;
5、DC=DE或BC=BE或OA=OE等;6、①②③
二、选择题:BBDA
课后测评
1.(1)不一定全等,因△ABP与△PCD中,只有AB=CD,而其它角和边都有可能不相等,故两三角形不一定全等。
(2)面积相等,因为OP为∠MON平分线上一点,故P到边AB、CD上的距离相等,即△ABP中AB边上的高与△PCD中CD边上的高相等,又根据AB=CD(即底边也相等)从而△ABP与△PCD的面积相等。
2.提示:根据等角的余角相等,可证AFE=BED,又因为BED=AEF,所以AFE=AEF。
3.提示:连结OA,OC,证AOB≌COD
4.提示:连结DB、DC。根据线段中垂线的性质,可得DB=DC,根据角平分线的性质,可得DM=DN,
因此,可得≌。
中考链接
1.D
2.D
3.A
4.A
5.3
2.在△ABC和△DCB中
,
∴△ABC≌△DCB
(SSS)
∴∠A=∠D
C
B
A
E
D
A
B
C
D
F
E
A
B
C
D
E
F
C
E
A
D
B
P
PAGE
5
中考要求
1.了解全等三角形的有关概念。
2.探索两个三角形全等的条件。
3.掌握两个三角形全等的条件。
4.解决全等三角形与其他知识的综合问题。
知识梳理
3.角平分线的性质:到角平分线上的点到角的两边的距离相等.
4.角平分线性质的逆定理:到角两边距离相等的点在角的平分线上.
典例解析
例1.阅读下题:如图,P是△ABC中BC边上一点,E是AP上的一点,若EB=EC,∠1=∠2,
求证:AP⊥BC。
证明:在△ABE和△ACE中,EB=EC,AE=AE,∠1=∠2
∴△ABE≌△ACE(第一步)
∴AB=AC,∠3=∠4(第二步)
∴AP⊥BC(等腰三角形三线合一)
上面的证明过程是否正确?若正确,请写出每一步的推理依据;若不正确,
请指出关键错在哪一步,并写出你认为正确的证明过程。
例2.已知:AB、CD相交于点O,AC∥DB,OC=OD,E、F为AB上两点,且AE=BF.求证:CE=DF
例3.如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD。
分析:采用截长补短法,延长AC至
E,使AE=AB,连结DE;也可在AB上
截取AE=AC,
再证明EB=CD(证明略)。
例4.如图,已知AB⊥BC,DC⊥BC,E在BC上,AE=AD,AB=BC。求证:CE=CD。
分析:作AF⊥CD的延长线,寻求全等的条件,在证明两条线段(或两个角)相等时,若它们所在的两个三角形不全等,就必须添加辅助线,构造全等三角形,常见辅助线有:①连结某两个已知点;②过已知点作某已知直线的平行线;③延长某已知线段到某个点,或与已知直线相交;④作一角等于已知角。
课堂检测
一、填空题:
1.若△ABC≌△EFG,且∠B=600,∠FGE-∠E=560,则∠A=
度。
2.如图,AB∥EF∥DC,∠ABC=900,AB=DC,那么图中有全等三角形
对。
3.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是
。
4.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:
,使△AEH≌△CEB。
5.如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O,写出一组相等的线段
(不包括AB=CD和AD=BC)。
6.如图,∠E=∠F=900,∠B=∠C,AE=AF。给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论是
(填序号)。
二、选择题:
1.如图,AD⊥AB,EA⊥AC,AE=AD,AB=AC,则下列结论中正确的是(
)
A.△ADF≌△AEG
B.△ABE≌△ACD
C.△BMF≌△CNG
D.△ADC≌△ABE
2.如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为(
)
A.600
B.700
C.750
D.850
3.如果两个三角形的两边和其中一边上的高分别对应相等,那么这两个三角形的第三边所对的角(
)
A.相等
B.不相等
C.互余
D.互补或相等
4.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=,PC=,AB=,AC=,则与的大小关系是(
)
A.>
B.<
C.=
D.无法确定
课后测评
1.如图,已知∠MON的边OM上有两点A、B,边ON上有两点C、D,且AB=CD,P为∠MON的平分线上一点。问:
(1)△ABP与△PCD是否全等?请说明理由。
(2)△ABP与△PCD的面积是否相等?请说明理由。
2.已知:中,BAC=90,AD是BC边上的高,BF平分ABC,交AD于E。
求证:AEF是等腰三角形
3.已知:如图AB=CD,AC和BD的垂直平分线相交于O点。
求证:ABO=CDO
4.已知:如图ABC中,BC边中垂线DE交BAC的平分线于D,DM⊥AB于M,DN⊥AC于N。
求证BM=CN
中考链接
1.如图所示:若△ABC≌△DEF∠A=50度,∠B=30度,则∠E等于(
)
A.30度??
B.50度
C.60度???
D.100度
2.如图所示:在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是(
)
A.15度??
B.20度
C.25度???
D.30
3.如图所示:点P是∠BAC的平分线AD上一点,
PE⊥AC于点E,
已知PE=3,
则点P到AB的距离是(
)
A.
3
B
。
4
C
。
5
D。
6
4.如图所示:在△ABC中,
已知∠ABC和∠ACB的平分线相交于F,
过点F作DE∥BC,交AB于点D,
交AC于点E,
若BD+CE=9,
则线段DE的长为(
)
A.9
B.8
C.7
D.6
5.如图所示:AB=AC,
EB=EC
,
AE的延长线交BC于D,那么图中的全等三角形共有
对
6.已知:如图,△ABC和△DBC的顶点A和D在BC的同旁,AB=DC,AC=DB,AC和DB相交于点O.求证:
∠A=∠D
全等三角形参考答案
课堂检测
一、填空题:
1、32;2、3;3、15;4、AH=BC或EA=EC或EH=EB等;
5、DC=DE或BC=BE或OA=OE等;6、①②③
二、选择题:BBDA
课后测评
1.(1)不一定全等,因△ABP与△PCD中,只有AB=CD,而其它角和边都有可能不相等,故两三角形不一定全等。
(2)面积相等,因为OP为∠MON平分线上一点,故P到边AB、CD上的距离相等,即△ABP中AB边上的高与△PCD中CD边上的高相等,又根据AB=CD(即底边也相等)从而△ABP与△PCD的面积相等。
2.提示:根据等角的余角相等,可证AFE=BED,又因为BED=AEF,所以AFE=AEF。
3.提示:连结OA,OC,证AOB≌COD
4.提示:连结DB、DC。根据线段中垂线的性质,可得DB=DC,根据角平分线的性质,可得DM=DN,
因此,可得≌。
中考链接
1.D
2.D
3.A
4.A
5.3
2.在△ABC和△DCB中
,
∴△ABC≌△DCB
(SSS)
∴∠A=∠D
C
B
A
E
D
A
B
C
D
F
E
A
B
C
D
E
F
C
E
A
D
B
P
PAGE
5
