人教版八年级上册数学课件:11.1与三角形有关线段综合复习(共18张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:11.1与三角形有关线段综合复习(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
11.1与三角形有关的线
段
综合复习
一、知识点归纳
?知识点一:三角形的相关概念
1.?三角形:①三条线段
②不在同一直线上
③首尾顺次相接
2.?三角形有三条边,三个顶点,三个角。
★在同一个三角形内,每一条边都有一个对角;每一个角都有一条对边
知识点二
:
三角形的分类
1.?三角形按边分类可分成不等边三角形和等腰三角形(等边三角形是一种特殊的等腰三角形)
2.?三角形按角分类可分成斜三角形(斜三角形包括锐角三角形钝角三角形)和直角三角形?。
知识点三:三角形的三边关系
三角形任意两边之和大于第三边,任意两边之差小于第三边。
知识点四??:三角形的主要线段:角平分线、中线、高线?
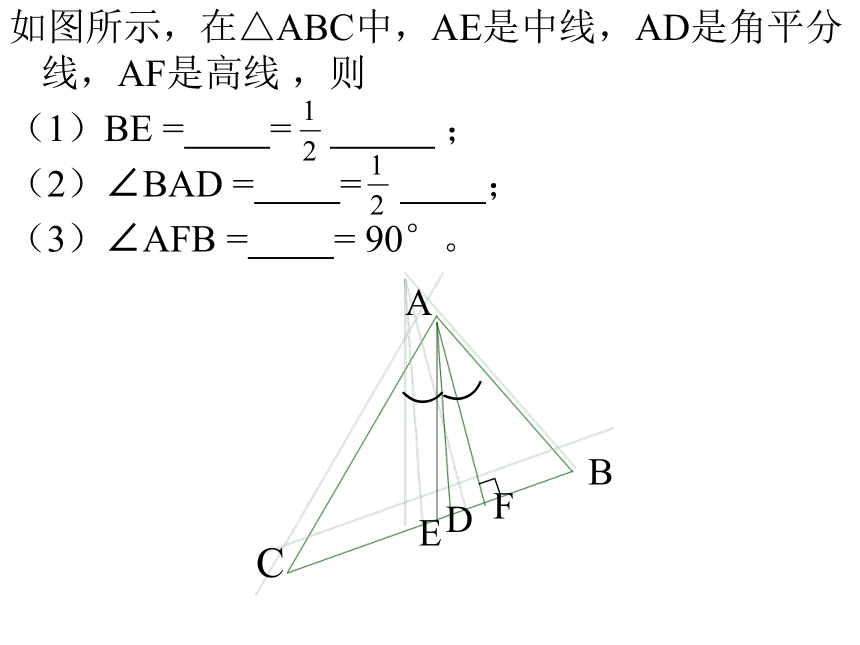
如图所示,在△ABC中,AE是中线,AD是角平分线,AF是高线?,则
(1)BE?=?????????=??
?
?;????
(2)∠BAD?=?????????=???
;????????
(3)∠AFB?=?????????=?90°。
∟
⌒
⌒
A
B
E
C
F
D
知识点五?:?三角形的稳定性?三角形具有稳定性;四边形不具有稳定性?
二?、?重点剖析
考点1:认识三角形
图11.1-1
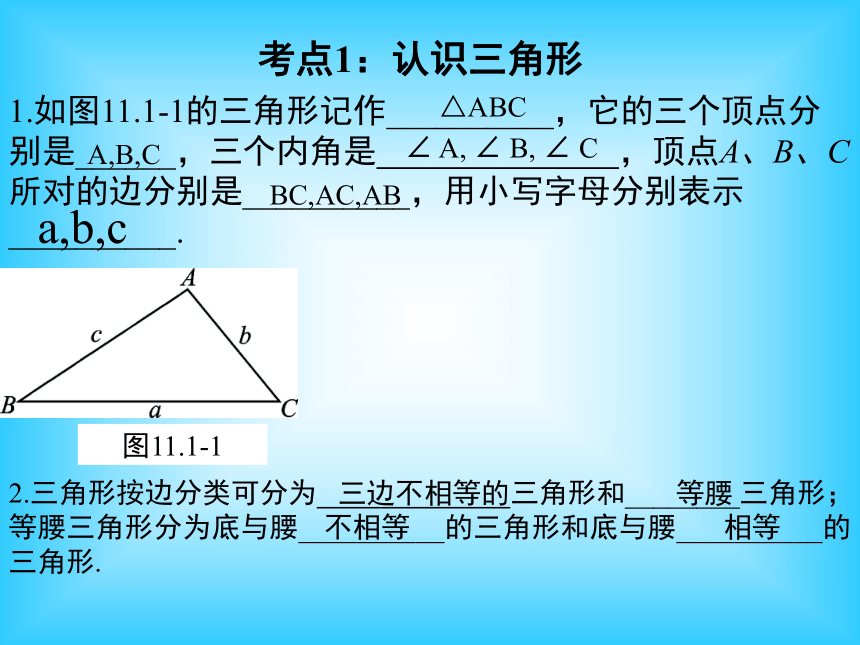
1.如图11.1-1的三角形记作__________,它的三个顶点分别是______,三个内角是
,顶点A、B、C所对的边分别是__________,用小写字母分别表示__________.
△ABC
A,B,C
∠
A,
∠
B,
∠
C
BC,AC,AB
a,b,c
2.三角形按边分类可分为
三角形和________三角形;等腰三角形分为底与腰__________的三角形和底与腰__________的三角形.
三边不相等的
等腰
不相等
相等
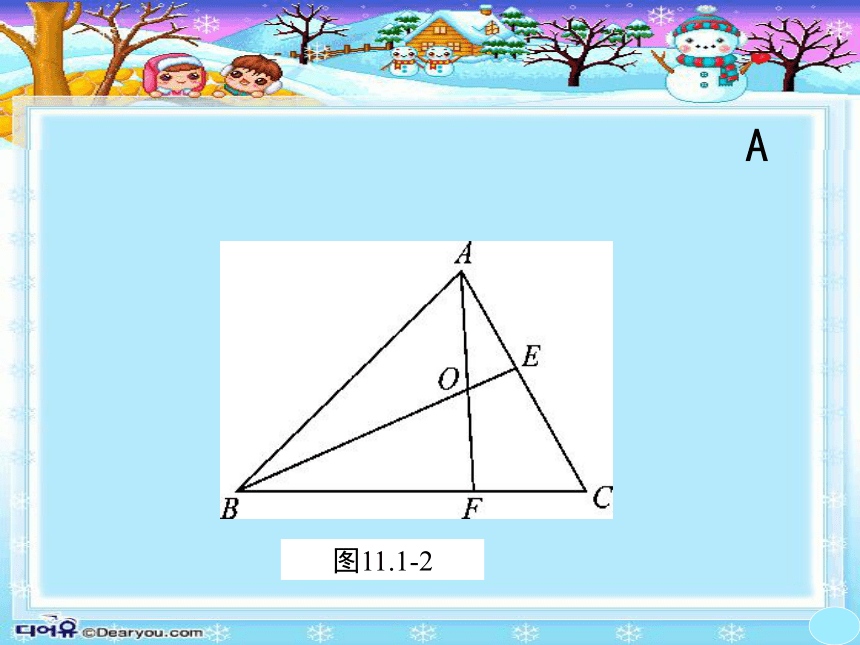
3.如图11.1-2所示,以AB为一边的三角形有(
)
A.3个
B.4个
C.5个
D.6个
图11.1-2
A
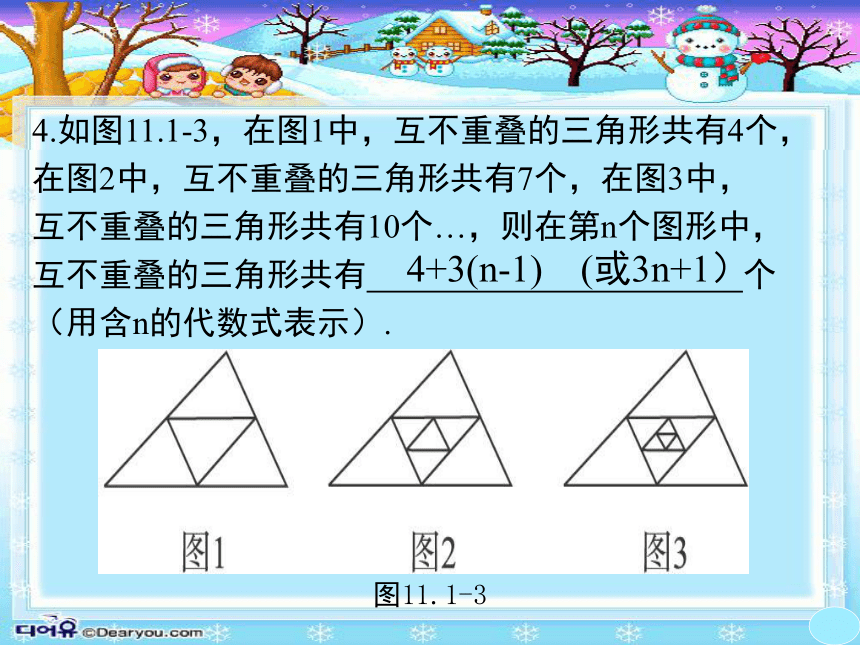
4.如图11.1-3,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个…,则在第n个图形中,互不重叠的三角形共有
个(用含n的代数式表示).
图11.1-3
4+3(n-1)
(或3n+1)
考点2:三角形三边关系
1、已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
2.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是(
)
A.1,2,3
B.2,5,8
C.3,4,5
D.4,5,10
3.已知三角形的三边长分别为4、5、x,则x不可能是(
)
A.3
B.5
C.7
D.9
B
C
D
4.已知三角形的两边长分别为4cm和9cm,则下列长度的
四条线段中能作为第三边的是(
)
A.13cm
B.6cm
C.5cm
D.4cm
5.一个三角形的两条边长分别为3和7,且第三边长为整
数
,这样的三角形的周长最小值是(
)
A.14
B.15
C.16
D.17
6.如果线段a、b、c能组成三角形,那么,它们的长度比
可能是
(
)
A.1∶2∶4
B.1∶3∶4
C.3∶4∶7
D.2∶3∶4
7.已知等腰三角形的两边长分别为4cm和7cm,则此三角
形的周长为(
)
A.15cm
B.18cm
C.15cm或18cm
D.不能确定
8.下列各组给出的三条线段中不能组成三角形的是(
)
A.3,4,5
B.3a,4a,5a
C.3+a,4+a,5+a
D.三条线段之比为3∶5∶8
B
B
D
C
D
9..三角形三边的比是3∶4∶5,周长是96cm,那么三边分别是
cm.
10.已知等腰三角形的周长是25cm,其中一边长为10cm,求另两边长
.
11.已知三角形的三边长分别为3,8,x;
若x的值为奇数,则x的值有___个;
12.已知等腰三角形的周长为21cm,若腰长为底边长的3倍,则其三边长分别为
;
13.如果△ABC是等腰三角形,试问:
⑴
若周长是18,一边长是8,则另两边长是
;
⑵
若周长是18,一边长是4,则另两边长是__________。
24,32,40
10,5或7.5,7.5cm
2
3,9,9cm
8,2或5,5
7,7
考点3:三角形的高
1.如图11.1-4,在△ABC中,BC边上的高是____;在△AFC中,CF边上的高是
;在△ABE中,AB边上的高是_____.
2.如图11.1-5,△ABC的三条高AD、BE、CF相交于点H,则△ABH的三条高是
,这三条高交于
.BD是△________、△________、△________的高.
图11.1-4
图11.1-5
AD
AF
BE
HF,AE,BD
点C
BDH
BHA
BDA
3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
5.三角形的三条高的交点一定在(
)
A.三角形内部
B.三角形的外部
C.三角形的内部或外部
D.以上答案都不对
B
D
考点4:三角形的中线与角平分线
1.如图11.1-6所示:
(1)AD⊥BC,垂足为D,则AD是
的高,∠________=∠________=90°.
(2)AE平分∠DAC,交DC于E点,则AE叫做△ADC的________,∠________=∠________=
∠________.
(3)若AF=FC,则△ABC的中线是________,S△ABF
=_______=
________
(4)若BG=GH=HF,则AG是________的中线,AH是__
______的中线.
图11.1-6
△
ABC
ADB
ADC
BF
S△CBF
角平分线
DAE
CAE
DAC
△
ABH
△
AGF
△ABC
2.如图11.1-7,DE∥BC,CD是∠ACB的平分线,∠ACB=60°,那么∠EDC=______度.
3.如图11.1-8,BD=DC,∠ABN=
∠ABC,则AD是△ABC的________线,BN是△ABC的________,
ND是△BNC的________线.
图11.1-7
图11.1-8
30
中
角平分线
中
4.下列判断中,正确的个数为(
)
(1)D是△ABC中BC边上的一个点,且BD=CD,则AD是△ABC的中线
(2)D是△ABC中BC边上的一个点,且∠ADC=90°,则AD是△ABC的高
(3)D是△ABC中BC边上的一个点,且∠BAD=
∠BAC,则AD是△ABC的角平分线
(4)三角形的中线、高、角平分线都是线段
A.1
B.2
C.3
D.4
C
5.如图11.1-9所示,在△ABC中,D、E分别是BC、AD的中点,S△ABC=4cm2,求S△ABE.
图11.1-9
考点5:三角形的稳定性
1.三角形是具有________的图形,而四边形没有_______.
2.自行车用脚架撑放比较稳定的原因是
.
3.下列把四边形的不稳定性合理地应用到生产实际中的例子有(
)
(1)活动挂架
(2)放缩尺
(3)屋顶钢架
(4)能够推拢和拉开的铁拉门(5)自行车的车架(6)大桥钢架
A.1
B.2
C.3
D.4
稳定性
稳定性
三角形具有稳定性
C
恳请指导!
多提宝贵意见!
11.1与三角形有关的线
段
综合复习
一、知识点归纳
?知识点一:三角形的相关概念
1.?三角形:①三条线段
②不在同一直线上
③首尾顺次相接
2.?三角形有三条边,三个顶点,三个角。
★在同一个三角形内,每一条边都有一个对角;每一个角都有一条对边
知识点二
:
三角形的分类
1.?三角形按边分类可分成不等边三角形和等腰三角形(等边三角形是一种特殊的等腰三角形)
2.?三角形按角分类可分成斜三角形(斜三角形包括锐角三角形钝角三角形)和直角三角形?。
知识点三:三角形的三边关系
三角形任意两边之和大于第三边,任意两边之差小于第三边。
知识点四??:三角形的主要线段:角平分线、中线、高线?
如图所示,在△ABC中,AE是中线,AD是角平分线,AF是高线?,则
(1)BE?=?????????=??
?
?;????
(2)∠BAD?=?????????=???
;????????
(3)∠AFB?=?????????=?90°。
∟
⌒
⌒
A
B
E
C
F
D
知识点五?:?三角形的稳定性?三角形具有稳定性;四边形不具有稳定性?
二?、?重点剖析
考点1:认识三角形
图11.1-1
1.如图11.1-1的三角形记作__________,它的三个顶点分别是______,三个内角是
,顶点A、B、C所对的边分别是__________,用小写字母分别表示__________.
△ABC
A,B,C
∠
A,
∠
B,
∠
C
BC,AC,AB
a,b,c
2.三角形按边分类可分为
三角形和________三角形;等腰三角形分为底与腰__________的三角形和底与腰__________的三角形.
三边不相等的
等腰
不相等
相等
3.如图11.1-2所示,以AB为一边的三角形有(
)
A.3个
B.4个
C.5个
D.6个
图11.1-2
A
4.如图11.1-3,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个…,则在第n个图形中,互不重叠的三角形共有
个(用含n的代数式表示).
图11.1-3
4+3(n-1)
(或3n+1)
考点2:三角形三边关系
1、已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为(
)
A.2cm
B.3cm
C.4cm
D.5cm
2.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是(
)
A.1,2,3
B.2,5,8
C.3,4,5
D.4,5,10
3.已知三角形的三边长分别为4、5、x,则x不可能是(
)
A.3
B.5
C.7
D.9
B
C
D
4.已知三角形的两边长分别为4cm和9cm,则下列长度的
四条线段中能作为第三边的是(
)
A.13cm
B.6cm
C.5cm
D.4cm
5.一个三角形的两条边长分别为3和7,且第三边长为整
数
,这样的三角形的周长最小值是(
)
A.14
B.15
C.16
D.17
6.如果线段a、b、c能组成三角形,那么,它们的长度比
可能是
(
)
A.1∶2∶4
B.1∶3∶4
C.3∶4∶7
D.2∶3∶4
7.已知等腰三角形的两边长分别为4cm和7cm,则此三角
形的周长为(
)
A.15cm
B.18cm
C.15cm或18cm
D.不能确定
8.下列各组给出的三条线段中不能组成三角形的是(
)
A.3,4,5
B.3a,4a,5a
C.3+a,4+a,5+a
D.三条线段之比为3∶5∶8
B
B
D
C
D
9..三角形三边的比是3∶4∶5,周长是96cm,那么三边分别是
cm.
10.已知等腰三角形的周长是25cm,其中一边长为10cm,求另两边长
.
11.已知三角形的三边长分别为3,8,x;
若x的值为奇数,则x的值有___个;
12.已知等腰三角形的周长为21cm,若腰长为底边长的3倍,则其三边长分别为
;
13.如果△ABC是等腰三角形,试问:
⑴
若周长是18,一边长是8,则另两边长是
;
⑵
若周长是18,一边长是4,则另两边长是__________。
24,32,40
10,5或7.5,7.5cm
2
3,9,9cm
8,2或5,5
7,7
考点3:三角形的高
1.如图11.1-4,在△ABC中,BC边上的高是____;在△AFC中,CF边上的高是
;在△ABE中,AB边上的高是_____.
2.如图11.1-5,△ABC的三条高AD、BE、CF相交于点H,则△ABH的三条高是
,这三条高交于
.BD是△________、△________、△________的高.
图11.1-4
图11.1-5
AD
AF
BE
HF,AE,BD
点C
BDH
BHA
BDA
3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
5.三角形的三条高的交点一定在(
)
A.三角形内部
B.三角形的外部
C.三角形的内部或外部
D.以上答案都不对
B
D
考点4:三角形的中线与角平分线
1.如图11.1-6所示:
(1)AD⊥BC,垂足为D,则AD是
的高,∠________=∠________=90°.
(2)AE平分∠DAC,交DC于E点,则AE叫做△ADC的________,∠________=∠________=
∠________.
(3)若AF=FC,则△ABC的中线是________,S△ABF
=_______=
________
(4)若BG=GH=HF,则AG是________的中线,AH是__
______的中线.
图11.1-6
△
ABC
ADB
ADC
BF
S△CBF
角平分线
DAE
CAE
DAC
△
ABH
△
AGF
△ABC
2.如图11.1-7,DE∥BC,CD是∠ACB的平分线,∠ACB=60°,那么∠EDC=______度.
3.如图11.1-8,BD=DC,∠ABN=
∠ABC,则AD是△ABC的________线,BN是△ABC的________,
ND是△BNC的________线.
图11.1-7
图11.1-8
30
中
角平分线
中
4.下列判断中,正确的个数为(
)
(1)D是△ABC中BC边上的一个点,且BD=CD,则AD是△ABC的中线
(2)D是△ABC中BC边上的一个点,且∠ADC=90°,则AD是△ABC的高
(3)D是△ABC中BC边上的一个点,且∠BAD=
∠BAC,则AD是△ABC的角平分线
(4)三角形的中线、高、角平分线都是线段
A.1
B.2
C.3
D.4
C
5.如图11.1-9所示,在△ABC中,D、E分别是BC、AD的中点,S△ABC=4cm2,求S△ABE.
图11.1-9
考点5:三角形的稳定性
1.三角形是具有________的图形,而四边形没有_______.
2.自行车用脚架撑放比较稳定的原因是
.
3.下列把四边形的不稳定性合理地应用到生产实际中的例子有(
)
(1)活动挂架
(2)放缩尺
(3)屋顶钢架
(4)能够推拢和拉开的铁拉门(5)自行车的车架(6)大桥钢架
A.1
B.2
C.3
D.4
稳定性
稳定性
三角形具有稳定性
C
恳请指导!
多提宝贵意见!
