人教版八年级上册数学12.2.1三角形全等的判定(SSS)课件(共22张PPT)
文档属性
| 名称 | 人教版八年级上册数学12.2.1三角形全等的判定(SSS)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 12:32:11 | ||
图片预览




文档简介
(共22张PPT)
12.2.1全等三角形判定(sss)
一、【学习目标】
1.知道三角形全等的性质和三角形全等的判定是两个相反的问题,领会三角形全等判定的意义。
2.通过画图,知道两个三角形具备三个条件的四种可能,渗透分类讨论思想能初步应用“边边边”条件判定两个三角形全等,会作一个角等于已知角。
3.会应用判定定理SSS进行简单的推理
二、【教学重、难点】
1、【教学重点】探究(只满足一个或两个条件的两个三角形不一
定全等)三角形全等的条件.
2、【教学难点】寻求三角形全等的条件.
三、【学习用具】圆规、直尺
四、【学习过程】
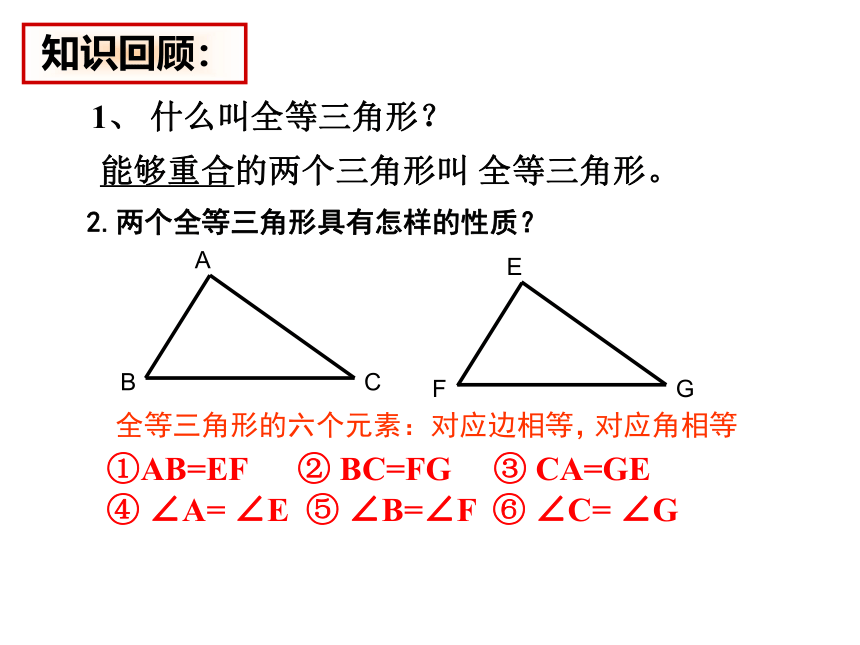
2.两个全等三角形具有怎样的性质?
E
F
G
A
B
C
全等三角形的六个元素:对应边相等,
1、
什么叫全等三角形?
能够重合的两个三角形叫
全等三角形。
知识回顾:
①AB=EF
②
BC=FG
③
CA=GE
对应角相等
④
∠A=
∠E
⑤
∠B=∠F
⑥
∠C=
∠G
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?
创设情境
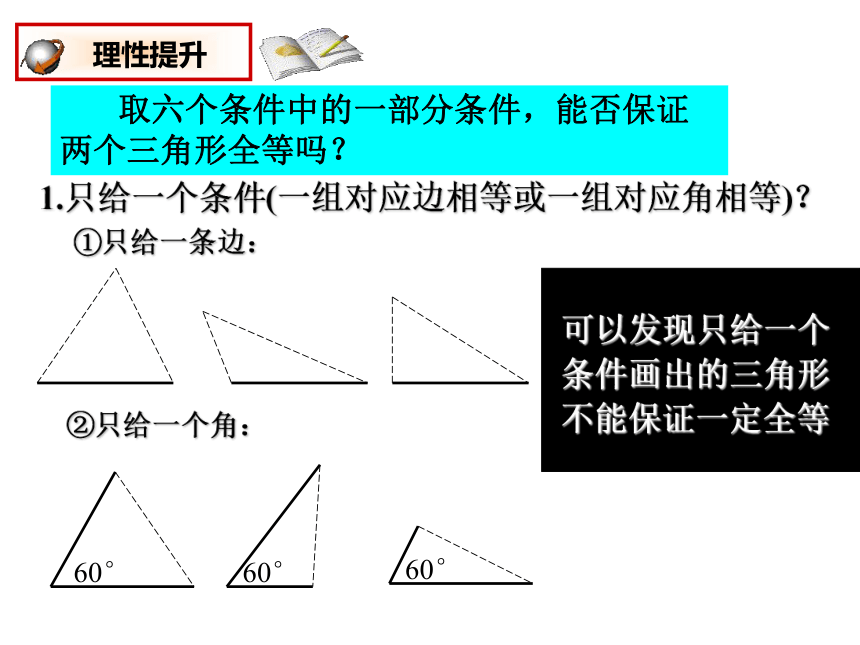
1.只给一个条件(一组对应边相等或一组对应角相等)?
①只给一条边:
②只给一个角:
60°
60°
60°
可以发现只给一个条件画出的三角形不能保证一定全等
理性提升
取六个条件中的一部分条件,能否保证两个三角形全等吗?
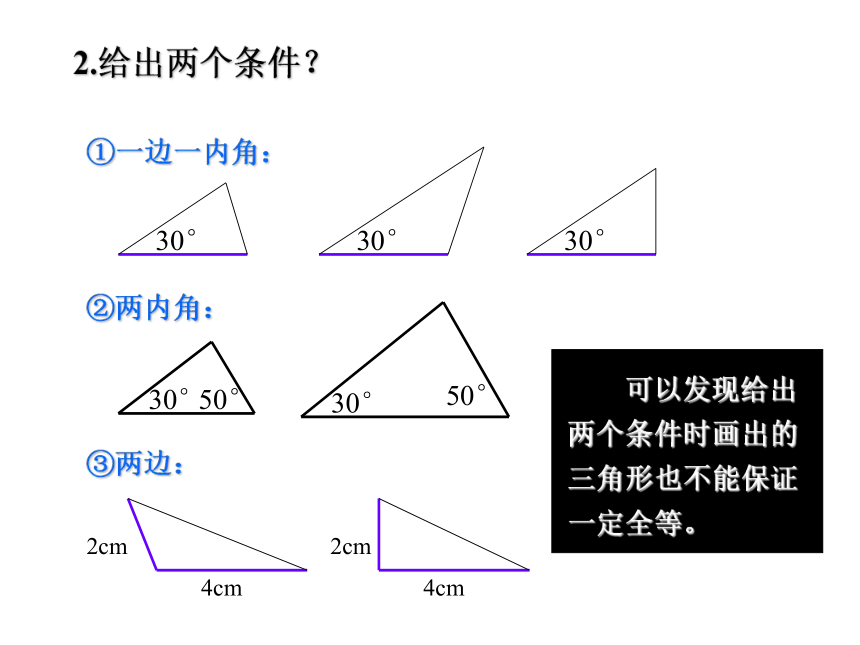
2.给出两个条件?
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现给出两个条件时画出的三角形也不能保证一定全等。
(2)
三角形的三个角对应相等。
3.三个条件呢?
(4)
三角形的一条边和两个角对应相等。
(1)
三角形的三条边对应相等。
(3)
三角形的两条边和一个角对应相等。
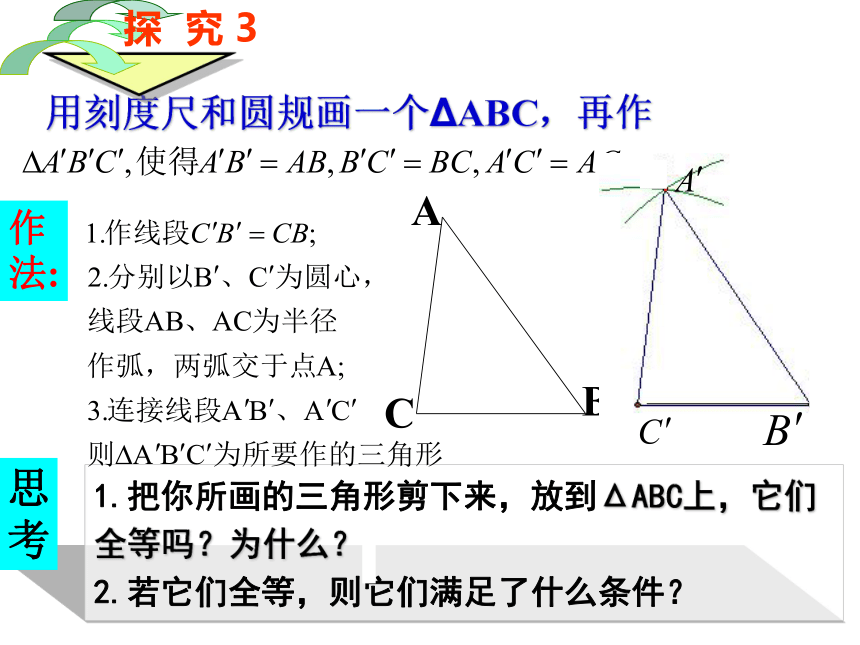
用刻度尺和圆规画一个ΔABC,再作
作
法:
1.把你所画的三角形剪下来,放到ΔABC上,它们全等吗?为什么?
2.若它们全等,则它们满足了什么条件?
探
究
3
A
C
B
思考
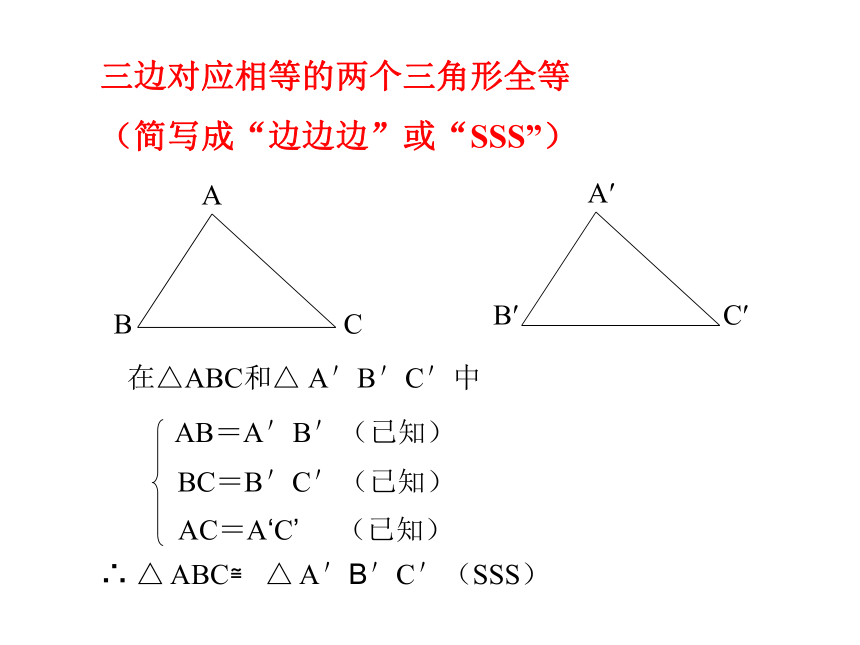
三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”)
A
B
C
A′
B′
C′
AB=A'B'(已知)
AC=A‘C’
(已知)
BC=B'C'(已知)
∴
△
ABC≌
△
A'B'C'(SSS)
在△ABC和△
A'B'C'中
三角形全等的判定1
C
A
B
D
O
议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
AO=DO(已知)
______=________(已知)
BO=CO(已知)
∴
△AOB≌△DOC(SSS)
AB
DC
解:
△ABC≌△DCB理由如下:
AB
=
CD
AC
=
DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件:
A
E
B
D
F
C
A
B
C
D
想一想
△ABC
≌
(
)
1、如图,AB=DC,AC=DB,△ABC和△DCB是否全等?试说
明理由。
△DCB
BC
CB
BF=CD
或
BD=CF
例1
已知:如图,AB=AD,BC=DC,
求证:△ABC≌
△ADC
A
B
C
D
AC
AC
(
)
≌
AB=AD
BC=CD
∴
△ABC
△ADC(SSS)
证明:在△ABC和△ADC中
=
公共边
A
C
B
D
分析:要证明两个三角形全等,需要那些条件?
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
例2
如图,
△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
△ABD≌△ACD
归纳:
①准备条件:证全等时要用的间接条件要
先证好;
②三角形全等书写三步骤:
写出:在哪两个三角形中
摆出:三个条件用大括号括起来
写出:全等结论
证明的书写步骤:
练习3、如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠
A=
∠
C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(公共边)
∴
∠
A=
∠
C
(全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
全等三角形的对应角相等
4.
已知:如图,
AC=FE,BC=DE,点
A,D,B,F在一条直线
上,AD=BF,
求证:∠E=∠C
A
B
D
F
E
C
证明:
∵
AD=FB
∴
∴
AD+DB=BF+DB
即AB=FD
在△ABC和△FDE中
AC=FE
BC=DE
AB=FD
△ABC≌△FDE
(SSS)
∴
∠E=∠C(
?
)
作图:即尺规作图(无刻度的直尺)
A
B
O
6如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.试说明∠A=∠D的理由。
∵BE=CF(已知)
即
BC=EF
在△ABC和△DEF中
AB=DE(已知)
AC=DF(已知)
BC=EF(已证)
∴△ABC≌△DEF(SSS)
∴∠A=∠D(全等三角形对应角相等)
F
A
B
E
C
D
∴
BE+EC=CF+EC
解:
?
挑战
自我
自主
合作
探究
互动
7.如图,小明在做数学作业时,遇到这样一个问题:
AB=CD,BC=DA,请说明∠A=∠C的道理。小明动手测
量了一下,发现∠A确实与∠C相等,但他
不能说明其中的道理,你能帮助他吗?
A
C
B
O
D
?
挑战
自我
已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
8:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
解:
①∵E、F分别是AB,CD的中点(
)
又∵AB=CD
∴AE=CF
在△ADE与△CBF中
AE=
=
∴△ADE≌△CBF
(
)
∴AE=
AB
CF=
CD(
)
1
2
1
2
9.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF
②∠A=∠C
线段中点的定义
CF
AD
DE
BF
SSS
△ADE≌△CBF
全等三角形对应角相等
已知
A
D
B
C
F
E
CB
②
∵
∴
∠A=∠C
(
)
=
1.
三边对应相等的两个三角形全等(边边边或SSS);
2.证明全等三角形书写格式:①准备条件;
②三角形全等书写的三步骤。
3、证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
小结归纳
1
12.2.1全等三角形判定(sss)
一、【学习目标】
1.知道三角形全等的性质和三角形全等的判定是两个相反的问题,领会三角形全等判定的意义。
2.通过画图,知道两个三角形具备三个条件的四种可能,渗透分类讨论思想能初步应用“边边边”条件判定两个三角形全等,会作一个角等于已知角。
3.会应用判定定理SSS进行简单的推理
二、【教学重、难点】
1、【教学重点】探究(只满足一个或两个条件的两个三角形不一
定全等)三角形全等的条件.
2、【教学难点】寻求三角形全等的条件.
三、【学习用具】圆规、直尺
四、【学习过程】
2.两个全等三角形具有怎样的性质?
E
F
G
A
B
C
全等三角形的六个元素:对应边相等,
1、
什么叫全等三角形?
能够重合的两个三角形叫
全等三角形。
知识回顾:
①AB=EF
②
BC=FG
③
CA=GE
对应角相等
④
∠A=
∠E
⑤
∠B=∠F
⑥
∠C=
∠G
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?
创设情境
1.只给一个条件(一组对应边相等或一组对应角相等)?
①只给一条边:
②只给一个角:
60°
60°
60°
可以发现只给一个条件画出的三角形不能保证一定全等
理性提升
取六个条件中的一部分条件,能否保证两个三角形全等吗?
2.给出两个条件?
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现给出两个条件时画出的三角形也不能保证一定全等。
(2)
三角形的三个角对应相等。
3.三个条件呢?
(4)
三角形的一条边和两个角对应相等。
(1)
三角形的三条边对应相等。
(3)
三角形的两条边和一个角对应相等。
用刻度尺和圆规画一个ΔABC,再作
作
法:
1.把你所画的三角形剪下来,放到ΔABC上,它们全等吗?为什么?
2.若它们全等,则它们满足了什么条件?
探
究
3
A
C
B
思考
三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”)
A
B
C
A′
B′
C′
AB=A'B'(已知)
AC=A‘C’
(已知)
BC=B'C'(已知)
∴
△
ABC≌
△
A'B'C'(SSS)
在△ABC和△
A'B'C'中
三角形全等的判定1
C
A
B
D
O
议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
AO=DO(已知)
______=________(已知)
BO=CO(已知)
∴
△AOB≌△DOC(SSS)
AB
DC
解:
△ABC≌△DCB理由如下:
AB
=
CD
AC
=
DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件:
A
E
B
D
F
C
A
B
C
D
想一想
△ABC
≌
(
)
1、如图,AB=DC,AC=DB,△ABC和△DCB是否全等?试说
明理由。
△DCB
BC
CB
BF=CD
或
BD=CF
例1
已知:如图,AB=AD,BC=DC,
求证:△ABC≌
△ADC
A
B
C
D
AC
AC
(
)
≌
AB=AD
BC=CD
∴
△ABC
△ADC(SSS)
证明:在△ABC和△ADC中
=
公共边
A
C
B
D
分析:要证明两个三角形全等,需要那些条件?
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
例2
如图,
△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
△ABD≌△ACD
归纳:
①准备条件:证全等时要用的间接条件要
先证好;
②三角形全等书写三步骤:
写出:在哪两个三角形中
摆出:三个条件用大括号括起来
写出:全等结论
证明的书写步骤:
练习3、如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠
A=
∠
C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(公共边)
∴
∠
A=
∠
C
(全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
全等三角形的对应角相等
4.
已知:如图,
AC=FE,BC=DE,点
A,D,B,F在一条直线
上,AD=BF,
求证:∠E=∠C
A
B
D
F
E
C
证明:
∵
AD=FB
∴
∴
AD+DB=BF+DB
即AB=FD
在△ABC和△FDE中
AC=FE
BC=DE
AB=FD
△ABC≌△FDE
(SSS)
∴
∠E=∠C(
?
)
作图:即尺规作图(无刻度的直尺)
A
B
O
6如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.试说明∠A=∠D的理由。
∵BE=CF(已知)
即
BC=EF
在△ABC和△DEF中
AB=DE(已知)
AC=DF(已知)
BC=EF(已证)
∴△ABC≌△DEF(SSS)
∴∠A=∠D(全等三角形对应角相等)
F
A
B
E
C
D
∴
BE+EC=CF+EC
解:
?
挑战
自我
自主
合作
探究
互动
7.如图,小明在做数学作业时,遇到这样一个问题:
AB=CD,BC=DA,请说明∠A=∠C的道理。小明动手测
量了一下,发现∠A确实与∠C相等,但他
不能说明其中的道理,你能帮助他吗?
A
C
B
O
D
?
挑战
自我
已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
8:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
解:
①∵E、F分别是AB,CD的中点(
)
又∵AB=CD
∴AE=CF
在△ADE与△CBF中
AE=
=
∴△ADE≌△CBF
(
)
∴AE=
AB
CF=
CD(
)
1
2
1
2
9.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF
②∠A=∠C
线段中点的定义
CF
AD
DE
BF
SSS
△ADE≌△CBF
全等三角形对应角相等
已知
A
D
B
C
F
E
CB
②
∵
∴
∠A=∠C
(
)
=
1.
三边对应相等的两个三角形全等(边边边或SSS);
2.证明全等三角形书写格式:①准备条件;
②三角形全等书写的三步骤。
3、证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
小结归纳
1
