五年级上册数学单元测试-第六单元多边形面积检测卷 冀教版(含解析)
文档属性
| 名称 | 五年级上册数学单元测试-第六单元多边形面积检测卷 冀教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 10:12:34 | ||
图片预览


文档简介
冀教版五年级上册数学第六单元检测卷
一、填空题。(17分)
1.8.08cm?________dm??? ???????? ? ? ? ? ? ? ? ? ? ? ? ???????????? 4900m?=________dm?
________m?=25dm?=________cm?? ??????????????3.54m?=________m?________dm?
2.一个平行四边形的底为5dm,高为4dm,面积是________dm?。
3.一个直角三角形的三条边分别是3厘米、4厘米、5厘米,它的面积是________cm?。
4.一个平行四边形的面积是12平方米,与它等底等高的三角形的面积是________。
5.一个平行四边形和一个三角形的面积相等,底也相等,三角形的高是6厘米,则平行四边形的高是________。
6.一个平行四边形的面积是60cm?,如果它的高缩小到原来的 13 ,底不变,面积是________。
7.一个梯形的面积是42平方分米,高是12分米,上底是3分米,下底是________分米。
8.一个等腰直角三角形的一条直角边是6厘米,则它的面积是________平方厘米。
9.一个直角梯形的下底是8cm,如果把上底增加3cm,它就变成了一个正方形,这个梯形的面积是________cm?。
10.一个三角形的面积是32dm?,高是40cm,底边是________dm。
11.把一个长8厘米,宽4厘米的长方形框架拉成一个平行四边形后,它的面积减少了8平方厘米,若平行四边形的底是8厘米,则高是________厘米。
12.一个梯形,高是16厘米,面积是240平方厘米,如果把梯形的下底延长10厘米,上底和高都不变,新梯形的面积是________平方厘米。
二、判断题。(9分)
13.两个面积相等的三角形,它们的底和高一定相等。( ????)
14.周长相等的长方形和平行四边形,面积不一定相等。(? ???)
15.一个三角形的底和高都扩大到原来的2倍,则面积也扩大到原来的2倍。(?? )
16.把一个平行四边形框架拉成一个长方形,周长不变,面积变小。(?? )
17.平行四边形的面积是三角形面积的2倍。(???? )
18.等底等高的两个三角形面积一定相等,但形状不一定相同。(?? )
19.把一个平行四边形分成两个大小相同的梯形,这两个梯形的高一定相等。(?? )
20.两个三角形的面积相等,底和高也一定相等。(?? )
21.在一个平行四边形内画一个最大的三角形,三角形的面积是平行四边形面积的一半。(?? )
三、选择题。(10分)
22.两个平行四边形的面积相等,它们的底和高(?? )。
A.?一定相等????????????????????????????????B.?一定不相等????????????????????????????????C.?不一定相等
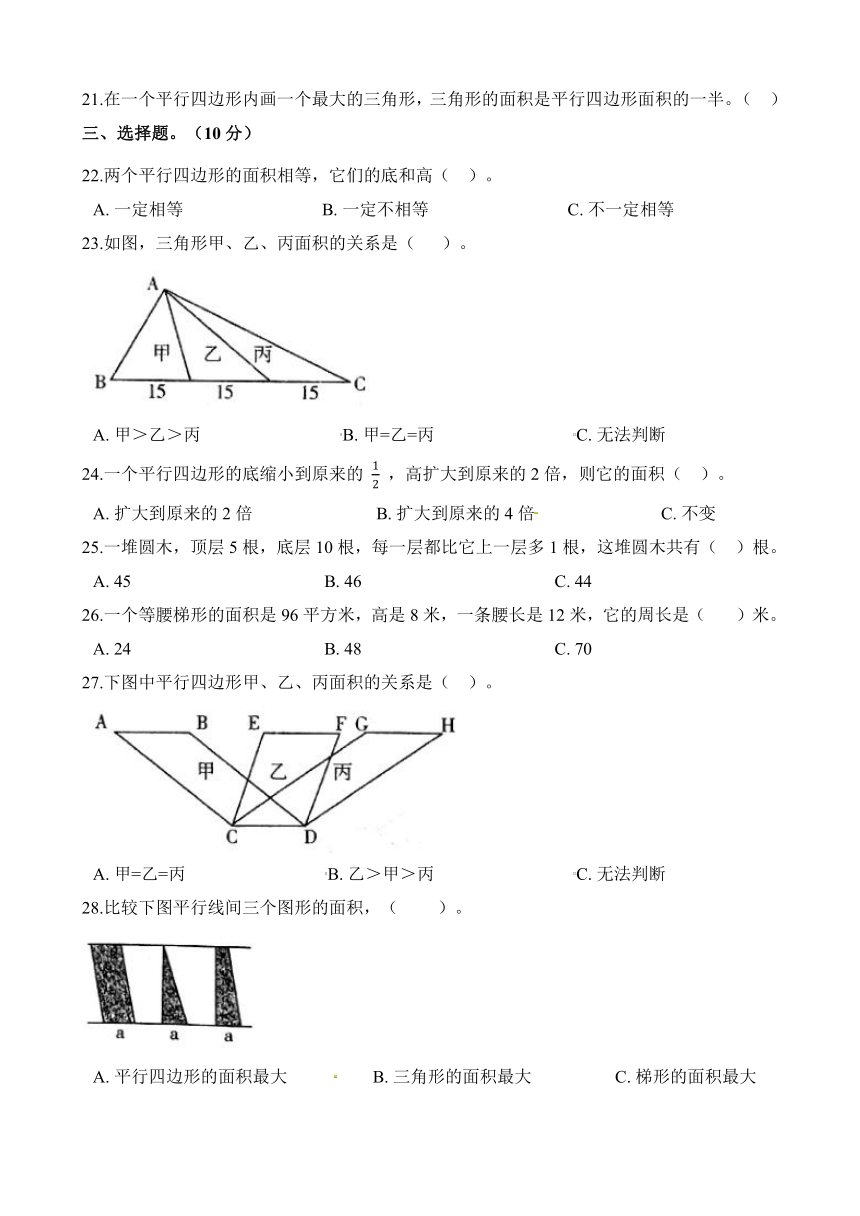
23.如图,三角形甲、乙、丙面积的关系是(? ???)。
A.?甲>乙>丙????????????????????????????????B.?甲=乙=丙????????????????????????????????C.?无法判断
24.一个平行四边形的底缩小到原来的 12 ,高扩大到原来的2倍,则它的面积(?? )。
A.?扩大到原来的2倍????????????????????????????B.?扩大到原来的4倍????????????????????????????C.?不变
25.一堆圆木,顶层5根,底层10根,每一层都比它上一层多1根,这堆圆木共有(?? )根。
A.?45????????????????????????????????????????????B.?46????????????????????????????????????????????C.?44
26.一个等腰梯形的面积是96平方米,高是8米,一条腰长是12米,它的周长是(????? )米。
A.?24????????????????????????????????????????????B.?48????????????????????????????????????????????C.?70
27.下图中平行四边形甲、乙、丙面积的关系是(?? )。
A.?甲=乙=丙????????????????????????????????B.?乙>甲>丙????????????????????????????????C.?无法判断
28.比较下图平行线间三个图形的面积,( ?? ? )。
A.?平行四边形的面积最大???????????????????B.?三角形的面积最大???????????????????C.?梯形的面积最大
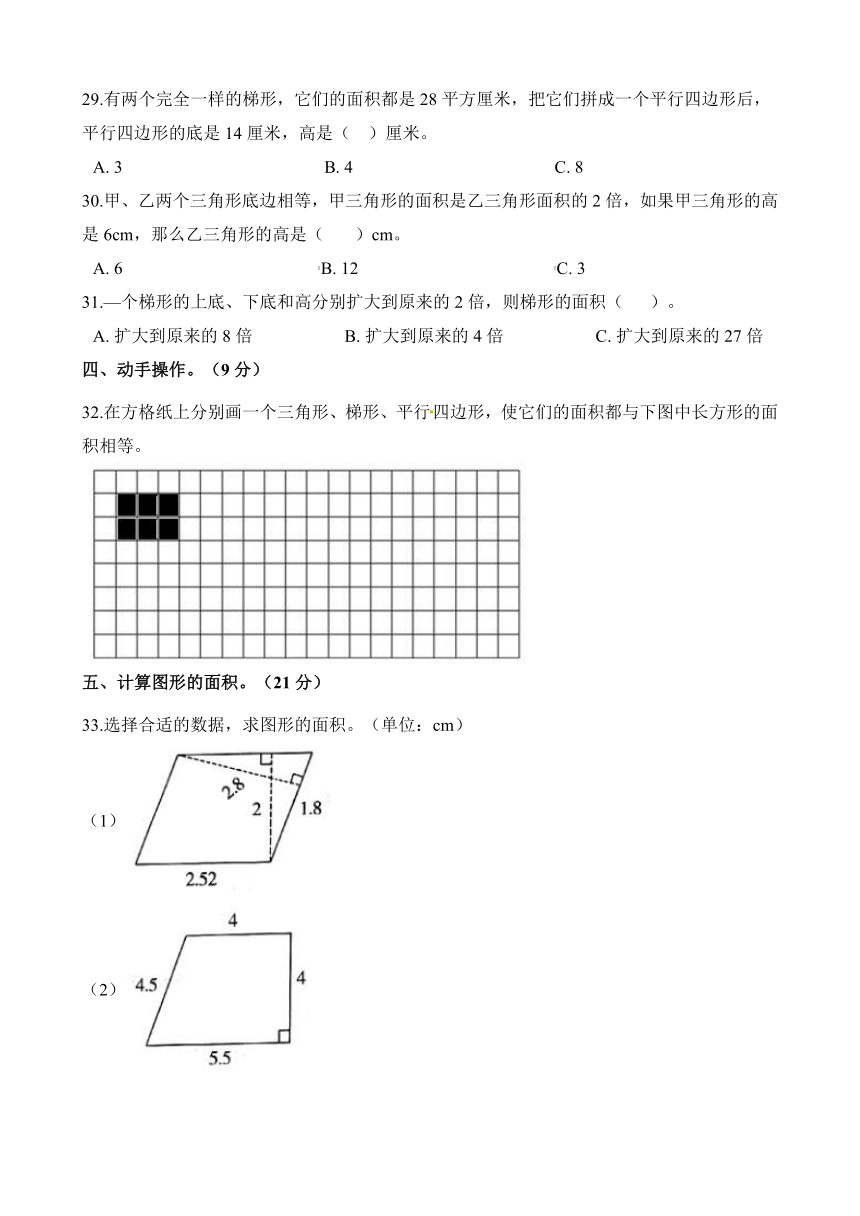
29.有两个完全一样的梯形,它们的面积都是28平方厘米,把它们拼成一个平行四边形后,平行四边形的底是14厘米,高是(?? )厘米。
A.?3??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?8
30.甲、乙两个三角形底边相等,甲三角形的面积是乙三角形面积的2倍,如果甲三角形的高是6cm,那么乙三角形的高是(? ?? )cm。
A.?6?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?3
31.—个梯形的上底、下底和高分别扩大到原来的2倍,则梯形的面积(???? )。
A.?扩大到原来的8倍?????????????????????B.?扩大到原来的4倍?????????????????????C.?扩大到原来的27倍
四、动手操作。(9分)
32.在方格纸上分别画一个三角形、梯形、平行四边形,使它们的面积都与下图中长方形的面积相等。
五、计算图形的面积。(21分)
33.选择合适的数据,求图形的面积。(单位:cm)
(1)
(2)
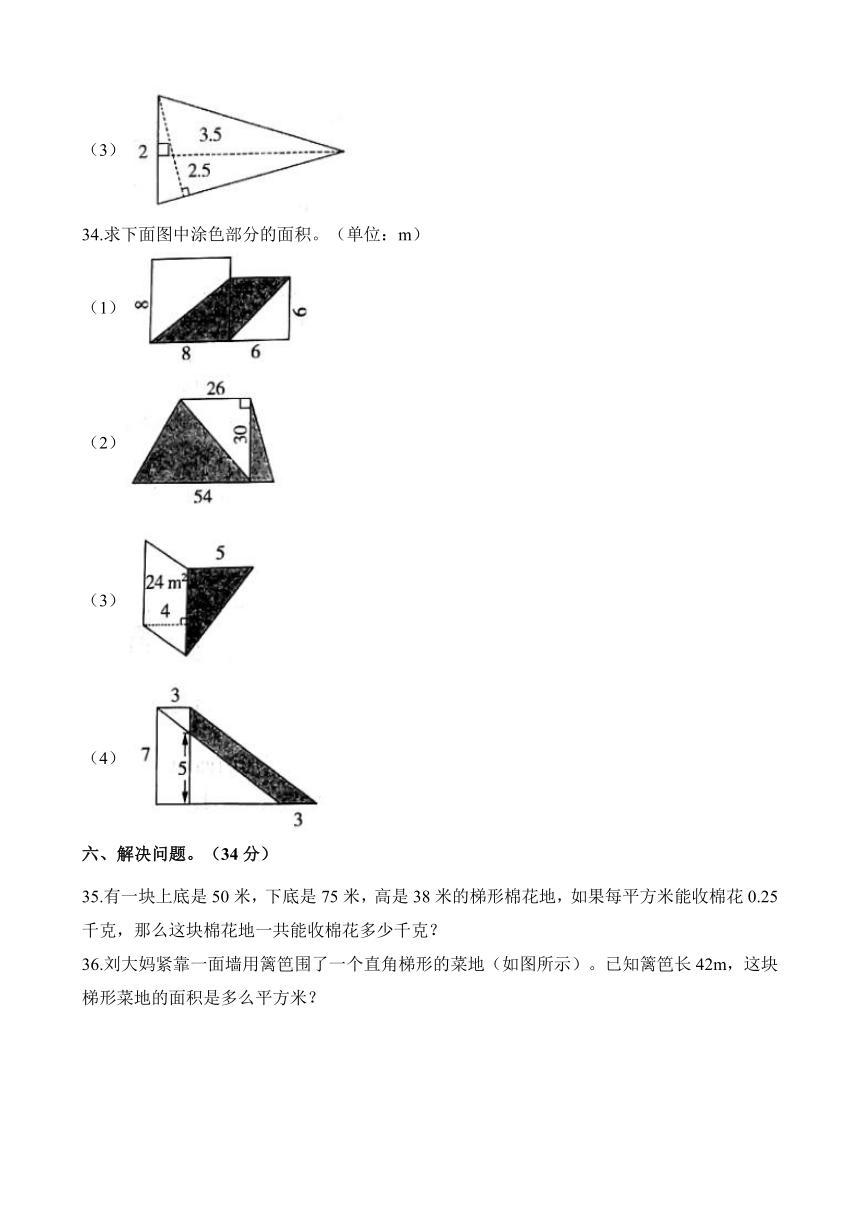
(3)
34.求下面图中涂色部分的面积。(单位:m)
(1)
(2)
(3)
(4)
六、解决问题。(34分)
35.有一块上底是50米,下底是75米,高是38米的梯形棉花地,如果每平方米能收棉花0.25千克,那么这块棉花地一共能收棉花多少千克?
36.刘大妈紧靠一面墙用篱笆围了一个直角梯形的菜地(如图所示)。已知篱笆长42m,这块梯形菜地的面积是多么平方米?
37.国光超市为了迎接“十周年店庆”,准备用长10m,宽2m的长方形红布做成直角边都是5dm的三角形小红旗,这块红布可以做几面这样的小红旗?
38.下面是一块长方形的麦田,中间有两条人行道。
(1)实际种植小麦的面积是多少平方米?
(2)如果每平方米麦田产小麦1.3千克,那么这块麦田共产小麦多少千克?
39.如图,梯形被分成了两个三角形,大三角形的面积是80平方米,底a是16米,小三角形的面积是60平方米,小三角形的底b是多少?
40.如下图所示,四边形ABCD是一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
答案解析部分
一、填空题。(17分)
1.【答案】 0.0808;490000;0.25;2500;3;54
【考点】平方厘米、平方分米、平方米之间的换算与比较
【解析】【解答】解:8.08÷100=0.0808dm2;4900×100=490000dm2;
25÷100=0.25m2、25×100=2500cm2;0.54×100=54dm2 , 所以3.54m2=3m254dm2。
故答案为:0.0808;490000;0.25;2500;3;54。
【分析】1m2=100dm2、1dm2=100cm2 , 高级单位转化为低级单位乘以进率,低级单位转化为高级单位除以进率。
2.【答案】 20
【考点】平行四边形的面积
【解析】【解答】解:面积=5×4=20(dm2)
故答案为:20。
【分析】平行四边形的面积=底×高,代入数值计算即可。
3.【答案】 6
【考点】三角形的面积
【解析】【解答】解:直角边分别是3厘米、4厘米,
所以面积=3×4÷2
=12÷2
=6(cm2)。
故答案为:6。
【分析】直角三角形的面积=两条直角边的乘积÷2,由于直角三角形的斜边均大于两条直角边,所以3厘米和4厘米是直角三角形的两条直角边,代入数值计算即可。
4.【答案】 6平方米
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:12÷2=6(平方米)
所以与平行四边形等底等高的三角形的面积是6平方米。
故答案为:6平方米。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,所以平行四边形与三角形等底等高时,三角形的面积=平行四边形的面积÷2,代入数值计算即可。
5.【答案】 3厘米
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:6÷2=3(厘米)
所以平行四边形的高是3厘米。
故答案为:3厘米。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,当平行四边形的面积、底分别与三角形的面积、底相等时,则平行四边形的高=三角形的高÷2,代入数值计算即可。
6.【答案】 20cm2
【考点】平行四边形的面积
【解析】【解答】解:60×13=20(cm2),
所以底不变,面积是20cm2。
故答案为:20cm2。
【分析】平行四边形的面积=底×高,底不变时,高缩小几倍(几分之几)则面积也缩小几倍(几分之几),代入数值计算即可。
7.【答案】 4
【考点】梯形的面积
【解析】【解答】解:42×2÷12-3
=84÷12-3
=7-3
=4(分米)
所以下底是4分米。
故答案为:4。
【分析】梯形的面积=(上底+下底)×高÷2,可得出下底=梯形的面积×2÷高-上底,代入数值计算即可。
8.【答案】 18
【考点】三角形的面积
【解析】【解答】解:6×6÷2
=36÷2
=18(平方厘米)
所以它的面积是18平方厘米。
故答案为:18。
【分析】等腰直角三角形的两条直角边相等,根据直角三角形的面积=两条直角边的乘积÷2计算即可得出答案。
9.【答案】 52
【考点】梯形的面积
【解析】【解答】解:梯形的面积=(8-3+8)×8÷2
=13×8÷2
=104÷2
=52(cm2)
故答案为:52。
【分析】根据将直角梯形的上底加上3厘米可得出一个正方形可得梯形的上底=下底-3厘米,梯形的高=下底,再根据梯形的面积=(上底+下底)×高÷2,代入数值计算即可。
10.【答案】 16
【考点】三角形的面积
【解析】【解答】解:40cm=4分米,
底边=32×2÷4
=64÷4
=16(分米)
故答案为:16。
【分析】先将单位统一,将厘米化成分米,再根据三角形的面积=底×高÷2得出三角形的底边=三角形的面积×2÷高,代入数值计算即可。
11.【答案】 3
【考点】平行四边形的面积,长方形的特征及性质,平行四边形的特征及性质
【解析】【解答】解:(8×4-8)÷8
=(32-8)÷8
=24÷8
=3(厘米)
所以平行四边形的高是3厘米。
故答案为:3。
【分析】长方形拉成平行四边形的过程中,底不变,高减小,长方形的面积=长×宽,平行四边形的面积=底×高,本题中平行四边形的高=(长方形的面积-长方形面积减少的平方厘米)÷平行四边形的底,代入数值计算即可。
12.【答案】 320
【考点】梯形的面积,三角形的面积
【解析】【解答】解:240+10×16÷2
=240+160÷2
=240+80
=320(平方厘米)
所以新梯形的面积是320平方厘米。
故答案为:320。
【分析】梯形的下底延长10厘米,上底和高不变,说明梯形的面积增加了一个底为10厘米、高为16厘米的三角形的面积,所以新梯形的面积=原来梯形的面积+一个底是10厘米、高是16厘米的三角形的面积(底×高÷2),代入数值计算即可。
二、判断题。(9分)
13.【答案】 错误
【考点】三角形的面积
【解析】【解答】解:两个面积相等的三角形,它们的底和高不一定相等,所以说法错误。
故答案为:错误。
【分析】采用举例法解答,例如面积是6平方厘米的三角形,三角形的底和高可能是6厘米、2厘米;也可能是4厘米、3厘米。
14.【答案】 正确
【考点】长方形的周长,平行四边形的面积,长方形的面积
【解析】【解答】解:周长相等的长方形和平行四边形,面积不一定相等,说法正确。
故答案为:正确。
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,周长相等的长方形和平行四边形,可将长方形拉成一个平行四边形,即这个过程中高减小,长方形的面积大于平行四边形的面积,本题据此解答。
15.【答案】 错误
【考点】三角形的面积
【解析】【解答】设原来三角的底和高分别是2厘米、1厘米,则
(2×2×1×2÷2)÷(2×1÷2)
=4÷1
=4
所以一个三角形的底和高都扩大到原来的2倍,则面积也扩大到原来的4倍。
故答案为:错误。
【分析】三角形的面积=底×高÷2,设原来三角的底和高分别是2厘米、1厘米,分别求出扩大后和扩大前三角形的面积,并相除即可得出答案。
16.【答案】 错误
【考点】平行四边形的面积,长方形的面积,平行四边形的特征及性质
【解析】【解答】解: 把一个平行四边形框架拉成一个长方形,周长不变,面积变大,所以说法错误。
故答案为:错误。
【分析】一个平行四边形框架拉成一个长方形的过程中,每条边的长度都不变,所以周长不变,但是平行四边形的高在变大,所以面积变大,本题据此解答。
17.【答案】错误
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:等底等高的平行四边形面积是三角形面积的2倍,原题说法错误.故答案为:错误
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的平行四边形面积是三角形面积的2倍.
18.【答案】 正确
【考点】三角形的面积
【解析】【解答】解: 等底等高的两个三角形面积一定相等,但形状不一定相同(如图),说法正确。
故答案为:正确。
【分析】三角形的面积=底×高÷2,只要三角形等底等高,那么三角形的面积一定相等。例如平行四边形ABCD中,连接AC、BD,则三角形ABC和三角形BCD的面积相等,但是形状不同。
19.【答案】 正确
【考点】平行四边形的特征及性质,梯形的特征及分类
【解析】【解答】解:把一个平行四边形分成两个大小相同的梯形,这两个梯形的高一定相等,说法正确。
故答案为:正确。
【分析】平行四边形分成的梯形必须是等底等高的梯形,否则拼起来就不是一个平行四边形,本题据此解答。
20.【答案】 错误
【考点】三角形的面积
【解析】【解答】 解:两个三角形的面积相等,底和高不一定相等,所以说法错误。
故答案为:错误。
【分析】三角形的面积=底×高÷2,例如面积为6平方厘米的三角形,它的底和高可能是6厘米、2厘米;也可能是4厘米、3厘米,本题据此解答。
21.【答案】 正确
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解: 在一个平行四边形内画一个最大的三角形,三角形的面积是平行四边形面积的一半,说法正确。
故答案为:正确。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,在平行四边形中画一个最大的三角形则三角形与平行四边形等底等高,根据面积公式即可得出答案。
三、选择题。(10分)
22.【答案】 C
【考点】平行四边形的面积
【解析】【解答】解:两个平行四边形的面积相等,它们的底和高不一定相等。
故答案为:C。
【分析】平行四边形的面积=底×高,例如面积是12平方厘米的平行四边形,平行四边形的底和高分别是6厘米、2厘米,也可以是4厘米、3厘米。
23.【答案】 B
【考点】三角形的面积
【解析】【解答】解:观察图形可得三角形等底同高,所以甲、乙、丙面积相等。
故答案为:B。
【分析】三角形的面积=底×高÷2,等底等高的三角形的面积相等,本题据此解答。
24.【答案】 C
【考点】平行四边形的面积
【解析】【解答】解:设平行四边形的底为2厘米,高为1厘米,则
原来平行四边形的面积=2×1=2(平方厘米)
变化后平行四边形的面积=2×12×1×2=2(平方厘米)
所以面积相等。
故答案为:C。
【分析】平行四边形的面积=底×高,设平行四边形的底为2厘米,高为1厘米,分别计算出原来平行四边形的面积以及变化后平行四边形的面积,比较即可得出答案。
25.【答案】 A
【考点】梯形的面积
【解析】【解答】解:(5+10)×6÷2
=15×6÷2
=90÷2
=45(根)
所以这堆圆木共有45根。
故答案为:A。
【分析】这堆圆木的上层5根,下层10根,层数是10-5+1,是一个等差数列5+6+7+8+9+10,也可以根据(上层的根数+下层的根数)×层数÷2计算。
26.【答案】 B
【考点】梯形的周长,梯形的面积
【解析】【解答】解:周长=96×2÷8+12×2
=192÷8+24
=24+24
=48(米)
故答案为:B。
【分析】梯形的面积=(上底+下底)×高÷2可得上底+下底=梯形的面积×2÷高;梯形的周长=上底+下底+腰长×2,代入数值计算即可。
27.【答案】 A
【考点】平行四边形的面积
【解析】【解答】解:观察图形可得平行四边形甲、乙、丙同底等高,所以面积相等。
故答案为:A。
【分析】平行四边形的面积=底×高,本题中甲、乙、丙的底边相同,高相等,即可得出答案。
28.【答案】 A
【考点】平行四边形的面积,梯形的面积,三角形的面积
【解析】【解答】解:观察图形可得平行四边形的面积最大。
故答案为:A。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,本题中平行四边形、三角形、梯形的高相等,平行四边形与三角形的底面相等,则平行四边形的面积大于三角形的面积;平行四边形的底与梯形的下底相同,只有当梯形的上底与下底相同时,两者面积相等,但题目上底小于下底,则平行四边形的面积大。
29.【答案】 B
【考点】平行四边形的面积,梯形的面积
【解析】【解答】解:28×2÷14
=56÷14
=4(厘米)
所以平行四边形的高是4厘米。
故答案为:B。
【分析】根据题意可得平行四边形的面积=2个梯形的面积之和,平行四边形的面积=底×高,则平行四边形的高=1个梯形的面积×2÷平行四边形的底,代入数值计算即可。
30.【答案】 C
【考点】三角形的面积
【解析】【解答】解:6÷2=3(cm)
所以乙三角形的高是3cm。
故答案为:C。
【分析】三角形的面积=底×高÷2,当两个三角形的底边相同时,三角形的面积与三角形的高成正比例,所以根据甲三角形的面积是乙三角形面积的2倍可得甲三角形的高是乙三角形高的2倍,根据甲三角形的高即可得出乙三角形的高。
31.【答案】 B
【考点】梯形的面积
【解析】【解答】解:设梯形的上底为1厘米,下底为2厘米,高为2厘米,则
[(1×2+2×2)×2×2÷2]÷[(1+2)×2÷2]
=[6×4÷2]÷[3×2÷2]
=12÷3
=4
所以梯形的面积扩大到原来的4倍。
故答案为:B。
【分析】梯形的面积=(上底+下底)×高÷2,设梯形的上底为1厘米,下底为2厘米,高为2厘米分别计算出扩大后和扩大前梯形的面积并相除即可得出答案。
四、动手操作。(9分)
32.【答案】
【考点】平行四边形的面积,梯形的面积,三角形的面积
【解析】【分析】三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,长方形的面积=长×宽,本题中长方形的面积是6,只需画出三角形,梯形、平行四边形的面积均是6即可。
五、计算图形的面积。(21分)
33.【答案】 (1)平行四边形的面积=2.52×2=5.04(cm2)或1.8×2.8=5.04(cm2)
(2)梯形的面积=(4+5.5)×4÷2
=9.5×4÷2
=19(cm2)
(3)3.5×2÷2=3.5(cm2)
【考点】平行四边形的面积,梯形的面积
【解析】【分析】(1)平行四边形的面积=底×高(高为底边上的高),代入数值计算即可;
(2)梯形的面积=(上底+下底)×高÷2,找出正确的高的值,计算即可;
(3)三角形的面积=底×高÷2,找出正确的高的值,计算即可。
34.【答案】 (1)阴影部分的面积=8×6÷2+6×6÷2
=24+18
=42(m2)
(2)阴影部分的面积=(26+54)×30÷2-26×30÷2
=80×30÷2-390
=1200-390
=810(m2)
(3)24÷4×5÷2
=6×5÷2
=15(m2)
(4)3×7-3×(7-5)÷2
=21-3×2÷2
=21-3
=18(m2)
【考点】平行四边形的面积,梯形的面积,组合图形面积的巧算,三角形的面积
【解析】【分析】(1)阴影部分的面积=底为8m,高为6m的三角形的面积+底为6m、高为6m的三角形的面积,再根据三角形的面积=底×高÷2,计算即可;
(2)阴影部分的面积=上底为26m、下底为54m、高为30m的梯形的面积-底为26m、高为30m的三角形的面积,梯形的面积=(上底+下底)×高÷2,计算即可;
(3)阴影部分的面积=以平行四边形的底边为高、以5m为底边的三角形的面积,根据平行四边形的面积=底×高即可得出平行四边形的底=平行四边形的面积÷高,计算即可;
(4)阴影部分的面积=底为3m、高为7m的平行四边形的面积-底为3m、高为(7-5)m的三角形的面积,计算即可。
六、解决问题。(34分)
35.【答案】 解:(50+75)×38÷2×0.25
=125×38÷2×0.75
=2375×0.75
=1781.25(千克)
答:这块棉花地一共能收棉花1781.25千克。
【考点】梯形的面积
【解析】【分析】这块棉花地一共能收棉花的千克数=棉花地的面积×每平方米能收棉花的千克数;棉花地的面积=(上底+下底)×高÷2,代入数值计算即可。
36.【答案】 解:(42-12)×12÷2
=30×12÷2
=360÷2
=180(平方米)
答:这块梯形菜地的面积是180平方米。
【考点】梯形的周长,梯形的面积
【解析】【分析】梯形的面积=(上底+下底)×高÷2,本题中梯形的上底+下底=篱笆的长度-梯形的高,梯形的高为12米,代入数值计算即可。
37.【答案】 解:10m=100dm,2m=20dm,
(10×20)÷(5×5÷2)
=200÷12.5
=16(面)
答:这块红布可以做16面这样的小旗。
【考点】三角形的面积,长方形的面积
【解析】【分析】先将单位统一,将m化成dm,再根据可以做小红旗的面数=长方形的面积(长×宽)÷三角形小红旗的面积(底×高÷2),代入数值计算即可。
38.【答案】 (1)解:实际种植小麦的面积=32×14-[(32-28)÷2×14×2]
=448-[4÷2×14×2]
=448-[2×14×2]
=448-56
=392(平方米)
答:实际种植小麦的面积是392平方米。
(2)解:392×1.3=509.6(千克)
答:这块麦田共产小麦509.6千克。
【考点】平行四边形的面积,组合图形面积的巧算,长方形的面积
【解析】【分析】(1)实际种植小麦的面积=长方形麦田的面积(长×宽)-两条人行道的面积(平行四边形的底是32-28的差再除以2,平行四边形的高为14m),计算即可;
(2)这块麦田共产小麦的千克数=实际种植小麦的面积× 每平方米麦田产小麦的千克数,计算即可。
39.【答案】 解:60×2÷(80×2÷16)
=120÷10
=12(米)
答:小三角形的底b是12米。
【考点】三角形的面积,梯形高的特点及画法
【解析】【分析】本题中大三角形和小三角形的高相等,三角形的面积=底×高÷2,先计算出大三角形的高,进而可计算出小三角形底b的值。
40.【答案】 解:将所有的小路靠边,可得出如图所示的图形:
小路的面积=20×2+14×2-2×2
=40+28-4
=64(平方米)
答:小路的面积是64平方米。
【考点】组合图形面积的巧算,长方形的面积,正方形的面积
【解析】【分析】将所有的小路都靠边,可得出小路的面积是一个长为20米、宽为2米的长方形的面积+一个长为14米、宽为2米的长方形的面积-重合部分的面积(边长为2米的正方形的面积),长方形的面积=长×宽,正方形的面积=边长×边长,代入数值计算即可。
一、填空题。(17分)
1.8.08cm?________dm??? ???????? ? ? ? ? ? ? ? ? ? ? ? ???????????? 4900m?=________dm?
________m?=25dm?=________cm?? ??????????????3.54m?=________m?________dm?
2.一个平行四边形的底为5dm,高为4dm,面积是________dm?。
3.一个直角三角形的三条边分别是3厘米、4厘米、5厘米,它的面积是________cm?。
4.一个平行四边形的面积是12平方米,与它等底等高的三角形的面积是________。
5.一个平行四边形和一个三角形的面积相等,底也相等,三角形的高是6厘米,则平行四边形的高是________。
6.一个平行四边形的面积是60cm?,如果它的高缩小到原来的 13 ,底不变,面积是________。
7.一个梯形的面积是42平方分米,高是12分米,上底是3分米,下底是________分米。
8.一个等腰直角三角形的一条直角边是6厘米,则它的面积是________平方厘米。
9.一个直角梯形的下底是8cm,如果把上底增加3cm,它就变成了一个正方形,这个梯形的面积是________cm?。
10.一个三角形的面积是32dm?,高是40cm,底边是________dm。
11.把一个长8厘米,宽4厘米的长方形框架拉成一个平行四边形后,它的面积减少了8平方厘米,若平行四边形的底是8厘米,则高是________厘米。
12.一个梯形,高是16厘米,面积是240平方厘米,如果把梯形的下底延长10厘米,上底和高都不变,新梯形的面积是________平方厘米。
二、判断题。(9分)
13.两个面积相等的三角形,它们的底和高一定相等。( ????)
14.周长相等的长方形和平行四边形,面积不一定相等。(? ???)
15.一个三角形的底和高都扩大到原来的2倍,则面积也扩大到原来的2倍。(?? )
16.把一个平行四边形框架拉成一个长方形,周长不变,面积变小。(?? )
17.平行四边形的面积是三角形面积的2倍。(???? )
18.等底等高的两个三角形面积一定相等,但形状不一定相同。(?? )
19.把一个平行四边形分成两个大小相同的梯形,这两个梯形的高一定相等。(?? )
20.两个三角形的面积相等,底和高也一定相等。(?? )
21.在一个平行四边形内画一个最大的三角形,三角形的面积是平行四边形面积的一半。(?? )
三、选择题。(10分)
22.两个平行四边形的面积相等,它们的底和高(?? )。
A.?一定相等????????????????????????????????B.?一定不相等????????????????????????????????C.?不一定相等
23.如图,三角形甲、乙、丙面积的关系是(? ???)。
A.?甲>乙>丙????????????????????????????????B.?甲=乙=丙????????????????????????????????C.?无法判断
24.一个平行四边形的底缩小到原来的 12 ,高扩大到原来的2倍,则它的面积(?? )。
A.?扩大到原来的2倍????????????????????????????B.?扩大到原来的4倍????????????????????????????C.?不变
25.一堆圆木,顶层5根,底层10根,每一层都比它上一层多1根,这堆圆木共有(?? )根。
A.?45????????????????????????????????????????????B.?46????????????????????????????????????????????C.?44
26.一个等腰梯形的面积是96平方米,高是8米,一条腰长是12米,它的周长是(????? )米。
A.?24????????????????????????????????????????????B.?48????????????????????????????????????????????C.?70
27.下图中平行四边形甲、乙、丙面积的关系是(?? )。
A.?甲=乙=丙????????????????????????????????B.?乙>甲>丙????????????????????????????????C.?无法判断
28.比较下图平行线间三个图形的面积,( ?? ? )。
A.?平行四边形的面积最大???????????????????B.?三角形的面积最大???????????????????C.?梯形的面积最大
29.有两个完全一样的梯形,它们的面积都是28平方厘米,把它们拼成一个平行四边形后,平行四边形的底是14厘米,高是(?? )厘米。
A.?3??????????????????????????????????????????????B.?4??????????????????????????????????????????????C.?8
30.甲、乙两个三角形底边相等,甲三角形的面积是乙三角形面积的2倍,如果甲三角形的高是6cm,那么乙三角形的高是(? ?? )cm。
A.?6?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?3
31.—个梯形的上底、下底和高分别扩大到原来的2倍,则梯形的面积(???? )。
A.?扩大到原来的8倍?????????????????????B.?扩大到原来的4倍?????????????????????C.?扩大到原来的27倍
四、动手操作。(9分)
32.在方格纸上分别画一个三角形、梯形、平行四边形,使它们的面积都与下图中长方形的面积相等。
五、计算图形的面积。(21分)
33.选择合适的数据,求图形的面积。(单位:cm)
(1)
(2)
(3)
34.求下面图中涂色部分的面积。(单位:m)
(1)
(2)
(3)
(4)
六、解决问题。(34分)
35.有一块上底是50米,下底是75米,高是38米的梯形棉花地,如果每平方米能收棉花0.25千克,那么这块棉花地一共能收棉花多少千克?
36.刘大妈紧靠一面墙用篱笆围了一个直角梯形的菜地(如图所示)。已知篱笆长42m,这块梯形菜地的面积是多么平方米?
37.国光超市为了迎接“十周年店庆”,准备用长10m,宽2m的长方形红布做成直角边都是5dm的三角形小红旗,这块红布可以做几面这样的小红旗?
38.下面是一块长方形的麦田,中间有两条人行道。
(1)实际种植小麦的面积是多少平方米?
(2)如果每平方米麦田产小麦1.3千克,那么这块麦田共产小麦多少千克?
39.如图,梯形被分成了两个三角形,大三角形的面积是80平方米,底a是16米,小三角形的面积是60平方米,小三角形的底b是多少?
40.如下图所示,四边形ABCD是一块长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
答案解析部分
一、填空题。(17分)
1.【答案】 0.0808;490000;0.25;2500;3;54
【考点】平方厘米、平方分米、平方米之间的换算与比较
【解析】【解答】解:8.08÷100=0.0808dm2;4900×100=490000dm2;
25÷100=0.25m2、25×100=2500cm2;0.54×100=54dm2 , 所以3.54m2=3m254dm2。
故答案为:0.0808;490000;0.25;2500;3;54。
【分析】1m2=100dm2、1dm2=100cm2 , 高级单位转化为低级单位乘以进率,低级单位转化为高级单位除以进率。
2.【答案】 20
【考点】平行四边形的面积
【解析】【解答】解:面积=5×4=20(dm2)
故答案为:20。
【分析】平行四边形的面积=底×高,代入数值计算即可。
3.【答案】 6
【考点】三角形的面积
【解析】【解答】解:直角边分别是3厘米、4厘米,
所以面积=3×4÷2
=12÷2
=6(cm2)。
故答案为:6。
【分析】直角三角形的面积=两条直角边的乘积÷2,由于直角三角形的斜边均大于两条直角边,所以3厘米和4厘米是直角三角形的两条直角边,代入数值计算即可。
4.【答案】 6平方米
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:12÷2=6(平方米)
所以与平行四边形等底等高的三角形的面积是6平方米。
故答案为:6平方米。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,所以平行四边形与三角形等底等高时,三角形的面积=平行四边形的面积÷2,代入数值计算即可。
5.【答案】 3厘米
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:6÷2=3(厘米)
所以平行四边形的高是3厘米。
故答案为:3厘米。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,当平行四边形的面积、底分别与三角形的面积、底相等时,则平行四边形的高=三角形的高÷2,代入数值计算即可。
6.【答案】 20cm2
【考点】平行四边形的面积
【解析】【解答】解:60×13=20(cm2),
所以底不变,面积是20cm2。
故答案为:20cm2。
【分析】平行四边形的面积=底×高,底不变时,高缩小几倍(几分之几)则面积也缩小几倍(几分之几),代入数值计算即可。
7.【答案】 4
【考点】梯形的面积
【解析】【解答】解:42×2÷12-3
=84÷12-3
=7-3
=4(分米)
所以下底是4分米。
故答案为:4。
【分析】梯形的面积=(上底+下底)×高÷2,可得出下底=梯形的面积×2÷高-上底,代入数值计算即可。
8.【答案】 18
【考点】三角形的面积
【解析】【解答】解:6×6÷2
=36÷2
=18(平方厘米)
所以它的面积是18平方厘米。
故答案为:18。
【分析】等腰直角三角形的两条直角边相等,根据直角三角形的面积=两条直角边的乘积÷2计算即可得出答案。
9.【答案】 52
【考点】梯形的面积
【解析】【解答】解:梯形的面积=(8-3+8)×8÷2
=13×8÷2
=104÷2
=52(cm2)
故答案为:52。
【分析】根据将直角梯形的上底加上3厘米可得出一个正方形可得梯形的上底=下底-3厘米,梯形的高=下底,再根据梯形的面积=(上底+下底)×高÷2,代入数值计算即可。
10.【答案】 16
【考点】三角形的面积
【解析】【解答】解:40cm=4分米,
底边=32×2÷4
=64÷4
=16(分米)
故答案为:16。
【分析】先将单位统一,将厘米化成分米,再根据三角形的面积=底×高÷2得出三角形的底边=三角形的面积×2÷高,代入数值计算即可。
11.【答案】 3
【考点】平行四边形的面积,长方形的特征及性质,平行四边形的特征及性质
【解析】【解答】解:(8×4-8)÷8
=(32-8)÷8
=24÷8
=3(厘米)
所以平行四边形的高是3厘米。
故答案为:3。
【分析】长方形拉成平行四边形的过程中,底不变,高减小,长方形的面积=长×宽,平行四边形的面积=底×高,本题中平行四边形的高=(长方形的面积-长方形面积减少的平方厘米)÷平行四边形的底,代入数值计算即可。
12.【答案】 320
【考点】梯形的面积,三角形的面积
【解析】【解答】解:240+10×16÷2
=240+160÷2
=240+80
=320(平方厘米)
所以新梯形的面积是320平方厘米。
故答案为:320。
【分析】梯形的下底延长10厘米,上底和高不变,说明梯形的面积增加了一个底为10厘米、高为16厘米的三角形的面积,所以新梯形的面积=原来梯形的面积+一个底是10厘米、高是16厘米的三角形的面积(底×高÷2),代入数值计算即可。
二、判断题。(9分)
13.【答案】 错误
【考点】三角形的面积
【解析】【解答】解:两个面积相等的三角形,它们的底和高不一定相等,所以说法错误。
故答案为:错误。
【分析】采用举例法解答,例如面积是6平方厘米的三角形,三角形的底和高可能是6厘米、2厘米;也可能是4厘米、3厘米。
14.【答案】 正确
【考点】长方形的周长,平行四边形的面积,长方形的面积
【解析】【解答】解:周长相等的长方形和平行四边形,面积不一定相等,说法正确。
故答案为:正确。
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,周长相等的长方形和平行四边形,可将长方形拉成一个平行四边形,即这个过程中高减小,长方形的面积大于平行四边形的面积,本题据此解答。
15.【答案】 错误
【考点】三角形的面积
【解析】【解答】设原来三角的底和高分别是2厘米、1厘米,则
(2×2×1×2÷2)÷(2×1÷2)
=4÷1
=4
所以一个三角形的底和高都扩大到原来的2倍,则面积也扩大到原来的4倍。
故答案为:错误。
【分析】三角形的面积=底×高÷2,设原来三角的底和高分别是2厘米、1厘米,分别求出扩大后和扩大前三角形的面积,并相除即可得出答案。
16.【答案】 错误
【考点】平行四边形的面积,长方形的面积,平行四边形的特征及性质
【解析】【解答】解: 把一个平行四边形框架拉成一个长方形,周长不变,面积变大,所以说法错误。
故答案为:错误。
【分析】一个平行四边形框架拉成一个长方形的过程中,每条边的长度都不变,所以周长不变,但是平行四边形的高在变大,所以面积变大,本题据此解答。
17.【答案】错误
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解:等底等高的平行四边形面积是三角形面积的2倍,原题说法错误.故答案为:错误
【分析】平行四边形面积=底×高,三角形面积=底×高÷2,等底等高的平行四边形面积是三角形面积的2倍.
18.【答案】 正确
【考点】三角形的面积
【解析】【解答】解: 等底等高的两个三角形面积一定相等,但形状不一定相同(如图),说法正确。
故答案为:正确。
【分析】三角形的面积=底×高÷2,只要三角形等底等高,那么三角形的面积一定相等。例如平行四边形ABCD中,连接AC、BD,则三角形ABC和三角形BCD的面积相等,但是形状不同。
19.【答案】 正确
【考点】平行四边形的特征及性质,梯形的特征及分类
【解析】【解答】解:把一个平行四边形分成两个大小相同的梯形,这两个梯形的高一定相等,说法正确。
故答案为:正确。
【分析】平行四边形分成的梯形必须是等底等高的梯形,否则拼起来就不是一个平行四边形,本题据此解答。
20.【答案】 错误
【考点】三角形的面积
【解析】【解答】 解:两个三角形的面积相等,底和高不一定相等,所以说法错误。
故答案为:错误。
【分析】三角形的面积=底×高÷2,例如面积为6平方厘米的三角形,它的底和高可能是6厘米、2厘米;也可能是4厘米、3厘米,本题据此解答。
21.【答案】 正确
【考点】平行四边形的面积,三角形的面积
【解析】【解答】解: 在一个平行四边形内画一个最大的三角形,三角形的面积是平行四边形面积的一半,说法正确。
故答案为:正确。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,在平行四边形中画一个最大的三角形则三角形与平行四边形等底等高,根据面积公式即可得出答案。
三、选择题。(10分)
22.【答案】 C
【考点】平行四边形的面积
【解析】【解答】解:两个平行四边形的面积相等,它们的底和高不一定相等。
故答案为:C。
【分析】平行四边形的面积=底×高,例如面积是12平方厘米的平行四边形,平行四边形的底和高分别是6厘米、2厘米,也可以是4厘米、3厘米。
23.【答案】 B
【考点】三角形的面积
【解析】【解答】解:观察图形可得三角形等底同高,所以甲、乙、丙面积相等。
故答案为:B。
【分析】三角形的面积=底×高÷2,等底等高的三角形的面积相等,本题据此解答。
24.【答案】 C
【考点】平行四边形的面积
【解析】【解答】解:设平行四边形的底为2厘米,高为1厘米,则
原来平行四边形的面积=2×1=2(平方厘米)
变化后平行四边形的面积=2×12×1×2=2(平方厘米)
所以面积相等。
故答案为:C。
【分析】平行四边形的面积=底×高,设平行四边形的底为2厘米,高为1厘米,分别计算出原来平行四边形的面积以及变化后平行四边形的面积,比较即可得出答案。
25.【答案】 A
【考点】梯形的面积
【解析】【解答】解:(5+10)×6÷2
=15×6÷2
=90÷2
=45(根)
所以这堆圆木共有45根。
故答案为:A。
【分析】这堆圆木的上层5根,下层10根,层数是10-5+1,是一个等差数列5+6+7+8+9+10,也可以根据(上层的根数+下层的根数)×层数÷2计算。
26.【答案】 B
【考点】梯形的周长,梯形的面积
【解析】【解答】解:周长=96×2÷8+12×2
=192÷8+24
=24+24
=48(米)
故答案为:B。
【分析】梯形的面积=(上底+下底)×高÷2可得上底+下底=梯形的面积×2÷高;梯形的周长=上底+下底+腰长×2,代入数值计算即可。
27.【答案】 A
【考点】平行四边形的面积
【解析】【解答】解:观察图形可得平行四边形甲、乙、丙同底等高,所以面积相等。
故答案为:A。
【分析】平行四边形的面积=底×高,本题中甲、乙、丙的底边相同,高相等,即可得出答案。
28.【答案】 A
【考点】平行四边形的面积,梯形的面积,三角形的面积
【解析】【解答】解:观察图形可得平行四边形的面积最大。
故答案为:A。
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,本题中平行四边形、三角形、梯形的高相等,平行四边形与三角形的底面相等,则平行四边形的面积大于三角形的面积;平行四边形的底与梯形的下底相同,只有当梯形的上底与下底相同时,两者面积相等,但题目上底小于下底,则平行四边形的面积大。
29.【答案】 B
【考点】平行四边形的面积,梯形的面积
【解析】【解答】解:28×2÷14
=56÷14
=4(厘米)
所以平行四边形的高是4厘米。
故答案为:B。
【分析】根据题意可得平行四边形的面积=2个梯形的面积之和,平行四边形的面积=底×高,则平行四边形的高=1个梯形的面积×2÷平行四边形的底,代入数值计算即可。
30.【答案】 C
【考点】三角形的面积
【解析】【解答】解:6÷2=3(cm)
所以乙三角形的高是3cm。
故答案为:C。
【分析】三角形的面积=底×高÷2,当两个三角形的底边相同时,三角形的面积与三角形的高成正比例,所以根据甲三角形的面积是乙三角形面积的2倍可得甲三角形的高是乙三角形高的2倍,根据甲三角形的高即可得出乙三角形的高。
31.【答案】 B
【考点】梯形的面积
【解析】【解答】解:设梯形的上底为1厘米,下底为2厘米,高为2厘米,则
[(1×2+2×2)×2×2÷2]÷[(1+2)×2÷2]
=[6×4÷2]÷[3×2÷2]
=12÷3
=4
所以梯形的面积扩大到原来的4倍。
故答案为:B。
【分析】梯形的面积=(上底+下底)×高÷2,设梯形的上底为1厘米,下底为2厘米,高为2厘米分别计算出扩大后和扩大前梯形的面积并相除即可得出答案。
四、动手操作。(9分)
32.【答案】
【考点】平行四边形的面积,梯形的面积,三角形的面积
【解析】【分析】三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,长方形的面积=长×宽,本题中长方形的面积是6,只需画出三角形,梯形、平行四边形的面积均是6即可。
五、计算图形的面积。(21分)
33.【答案】 (1)平行四边形的面积=2.52×2=5.04(cm2)或1.8×2.8=5.04(cm2)
(2)梯形的面积=(4+5.5)×4÷2
=9.5×4÷2
=19(cm2)
(3)3.5×2÷2=3.5(cm2)
【考点】平行四边形的面积,梯形的面积
【解析】【分析】(1)平行四边形的面积=底×高(高为底边上的高),代入数值计算即可;
(2)梯形的面积=(上底+下底)×高÷2,找出正确的高的值,计算即可;
(3)三角形的面积=底×高÷2,找出正确的高的值,计算即可。
34.【答案】 (1)阴影部分的面积=8×6÷2+6×6÷2
=24+18
=42(m2)
(2)阴影部分的面积=(26+54)×30÷2-26×30÷2
=80×30÷2-390
=1200-390
=810(m2)
(3)24÷4×5÷2
=6×5÷2
=15(m2)
(4)3×7-3×(7-5)÷2
=21-3×2÷2
=21-3
=18(m2)
【考点】平行四边形的面积,梯形的面积,组合图形面积的巧算,三角形的面积
【解析】【分析】(1)阴影部分的面积=底为8m,高为6m的三角形的面积+底为6m、高为6m的三角形的面积,再根据三角形的面积=底×高÷2,计算即可;
(2)阴影部分的面积=上底为26m、下底为54m、高为30m的梯形的面积-底为26m、高为30m的三角形的面积,梯形的面积=(上底+下底)×高÷2,计算即可;
(3)阴影部分的面积=以平行四边形的底边为高、以5m为底边的三角形的面积,根据平行四边形的面积=底×高即可得出平行四边形的底=平行四边形的面积÷高,计算即可;
(4)阴影部分的面积=底为3m、高为7m的平行四边形的面积-底为3m、高为(7-5)m的三角形的面积,计算即可。
六、解决问题。(34分)
35.【答案】 解:(50+75)×38÷2×0.25
=125×38÷2×0.75
=2375×0.75
=1781.25(千克)
答:这块棉花地一共能收棉花1781.25千克。
【考点】梯形的面积
【解析】【分析】这块棉花地一共能收棉花的千克数=棉花地的面积×每平方米能收棉花的千克数;棉花地的面积=(上底+下底)×高÷2,代入数值计算即可。
36.【答案】 解:(42-12)×12÷2
=30×12÷2
=360÷2
=180(平方米)
答:这块梯形菜地的面积是180平方米。
【考点】梯形的周长,梯形的面积
【解析】【分析】梯形的面积=(上底+下底)×高÷2,本题中梯形的上底+下底=篱笆的长度-梯形的高,梯形的高为12米,代入数值计算即可。
37.【答案】 解:10m=100dm,2m=20dm,
(10×20)÷(5×5÷2)
=200÷12.5
=16(面)
答:这块红布可以做16面这样的小旗。
【考点】三角形的面积,长方形的面积
【解析】【分析】先将单位统一,将m化成dm,再根据可以做小红旗的面数=长方形的面积(长×宽)÷三角形小红旗的面积(底×高÷2),代入数值计算即可。
38.【答案】 (1)解:实际种植小麦的面积=32×14-[(32-28)÷2×14×2]
=448-[4÷2×14×2]
=448-[2×14×2]
=448-56
=392(平方米)
答:实际种植小麦的面积是392平方米。
(2)解:392×1.3=509.6(千克)
答:这块麦田共产小麦509.6千克。
【考点】平行四边形的面积,组合图形面积的巧算,长方形的面积
【解析】【分析】(1)实际种植小麦的面积=长方形麦田的面积(长×宽)-两条人行道的面积(平行四边形的底是32-28的差再除以2,平行四边形的高为14m),计算即可;
(2)这块麦田共产小麦的千克数=实际种植小麦的面积× 每平方米麦田产小麦的千克数,计算即可。
39.【答案】 解:60×2÷(80×2÷16)
=120÷10
=12(米)
答:小三角形的底b是12米。
【考点】三角形的面积,梯形高的特点及画法
【解析】【分析】本题中大三角形和小三角形的高相等,三角形的面积=底×高÷2,先计算出大三角形的高,进而可计算出小三角形底b的值。
40.【答案】 解:将所有的小路靠边,可得出如图所示的图形:
小路的面积=20×2+14×2-2×2
=40+28-4
=64(平方米)
答:小路的面积是64平方米。
【考点】组合图形面积的巧算,长方形的面积,正方形的面积
【解析】【分析】将所有的小路都靠边,可得出小路的面积是一个长为20米、宽为2米的长方形的面积+一个长为14米、宽为2米的长方形的面积-重合部分的面积(边长为2米的正方形的面积),长方形的面积=长×宽,正方形的面积=边长×边长,代入数值计算即可。
