2020-2021学年新教材人教版必修第一册 4.3 牛顿第二定律 作业
文档属性
| 名称 | 2020-2021学年新教材人教版必修第一册 4.3 牛顿第二定律 作业 |  | |
| 格式 | doc | ||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-15 06:12:49 | ||
图片预览




文档简介
第3节 牛顿第二定律
必备知识基础练 进阶训练第一层
知识点一 牛顿第二定律
1.对静止在光滑水平面上的物体施加一水平拉力,当力刚开始作用的瞬间( )
A.物体立即获得速度
B.物体立即获得加速度
C.物体同时获得速度和加速度
D.由于物体未来得及运动,所以速度和加速度都为零
2.(多选)如图所示,当小车水平向右加速运动时,物块M相对静止于车厢后竖直壁上.当小车的加速度增大时( )
A.M所受的静摩擦力增大 B.M对车厢的作用力增大
C.M仍相对车厢静止 D.M受到的合外力为零
3.如图所示,位于水平地面上的质量为M的木块,在方向与水平面成α角、大小为F的拉力作用下,沿水平地面做匀加速直线运动,若木块与地面间的动摩擦因数为μ,则木块的加速度为( )
A. B.
C. D.
4.(多选)如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的较长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时( )
A.猫有向上的加速度
B.猫处于平衡状态,板对猫有沿斜面向上的摩擦力
C.板的加速度大小为gsin α,方向沿斜面向下
D.板的加速度大小为gsin α,方向沿斜面向下
知识点二 力的单位
5.一轻弹簧上端固定,下端挂一重物,平衡时弹簧伸长了4 cm,再将重物向下拉1 cm,然后放手,则在释放瞬间重物的加速度是(g取10 m/s2)( )
A.2.5 m/s2 B.7.5 m/s2
C.10 m/s2 D.12.5 m/s2
关键能力综合练 进阶训练第二层
一、单项选择题
1.由牛顿第二定律知,无论怎样小的力都可以使物体产生加速度,可是当我们用一个力推桌子没有推动时是因为( )
A.牛顿第二定律不适用于静止的物体
B.桌子的加速度很小,速度增量很小,眼睛不易觉察到
C.推力小于摩擦力,加速度是负值
D.推力、重力、地面的支持力与摩擦力的合力等于零,桌子的加速度为零,所以桌子仍静止
2.如图所示,放在光滑水平面上的一个物体,同时受到两个水平方向力的作用,其中水平向右的力F1=5 N,水平向左的力F2=10 N,当F2由10 N逐渐减小到零的过程中,物体的加速度大小变化情况是( )
A.逐渐减小 B.逐渐增大
C.先减小后增大 D.先增大后减小
3.力F作用于甲物体(质量为m1)时产生的加速度为a1,此力作用于乙物体(质量为m2)时产生的加速度为a2,若将甲、乙两个物体合在一起,仍受此力的作用.则产生的加速度是( )
A. B.
C. D.
4.(探究题)如图所示,天花板上用细绳吊起两个用轻弹簧相连的质量相同的小球,两小球均保持静止.已知重力加速度为g,当突然剪断细绳时,上面的小球A与下面的小球B的加速度为( )
A.aA=g,aB=g B.aA=g,aB=0
C.aA=2g,aB=0 D.aA=0,aB=g
5.如图所示,底板光滑的小车上用两个量程为0~20 N、完全相同的弹簧测力计甲和乙系住一个质量为1 kg的物块.在水平地面上,当小车做匀速直线运动时,两弹簧测力计的示数均为10 N,当小车做匀加速直线运动时,弹簧测力计甲的示数变为8 N.这时小车运动的加速度大小是( )
A.2 m/s2 B.4 m/s2
C.6 m/s2 D.8 m/s2
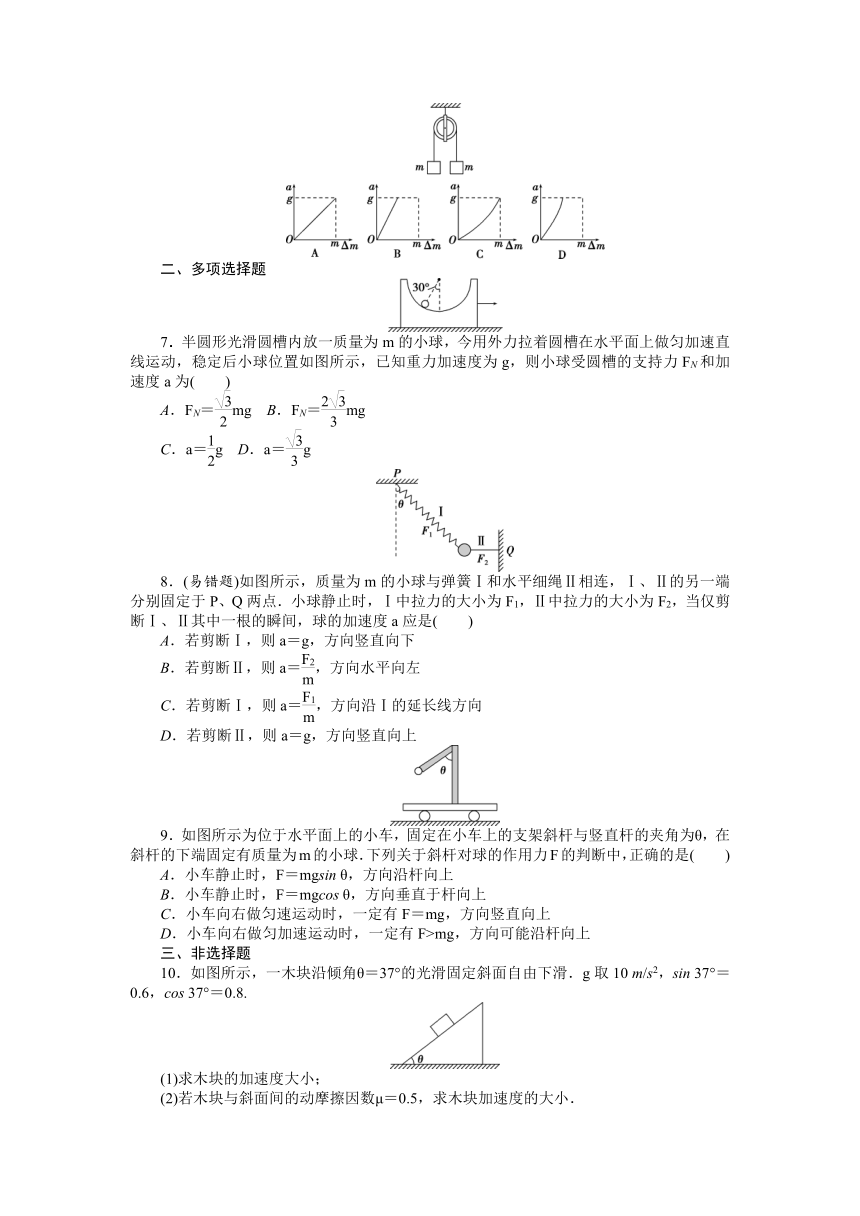
6.早在公元前4世纪末,我国的《墨经》中就有关于力和运动的一些见解,如“绳下直,权重相若则正矣.收,上者愈丧,下者愈得”,这句话所描述的情况与下述物理现象相似.如图,一根跨过定滑轮的轻绳两端各悬挂一重物,当两重物质量均为m时,系统处于平衡状态.若减小其中一个重物的质量,系统就无法保持平衡,上升的重物减小的质量Δm越多,另一个重物下降的加速度a就越大.已知重力加速度为g,则a与Δm的关系图像可能是( )
二、多项选择题
7.半圆形光滑圆槽内放一质量为m的小球,今用外力拉着圆槽在水平面上做匀加速直线运动,稳定后小球位置如图所示,已知重力加速度为g,则小球受圆槽的支持力FN和加速度a为( )
A.FN=mg B.FN=mg
C.a=g D.a=g
8.(易错题)如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.小球静止时,Ⅰ中拉力的大小为F1,Ⅱ中拉力的大小为F2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )
A.若剪断Ⅰ,则a=g,方向竖直向下
B.若剪断Ⅱ,则a=,方向水平向左
C.若剪断Ⅰ,则a=,方向沿Ⅰ的延长线方向
D.若剪断Ⅱ,则a=g,方向竖直向上
9.如图所示为位于水平面上的小车,固定在小车上的支架斜杆与竖直杆的夹角为θ,在斜杆的下端固定有质量为m的小球.下列关于斜杆对球的作用力F的判断中,正确的是( )
A.小车静止时,F=mgsin θ,方向沿杆向上
B.小车静止时,F=mgcos θ,方向垂直于杆向上
C.小车向右做匀速运动时,一定有F=mg,方向竖直向上
D.小车向右做匀加速运动时,一定有F>mg,方向可能沿杆向上
三、非选择题
10.如图所示,一木块沿倾角θ=37°的光滑固定斜面自由下滑.g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求木块的加速度大小;
(2)若木块与斜面间的动摩擦因数μ=0.5,求木块加速度的大小.
学科素养升级练 进阶训练第三层
1.(学术情境)来自北京工业大学的一群大学生,受“蜘蛛侠”的启发,研发出了独特的六爪攀壁蜘蛛机器人(如图甲).六爪攀壁蜘蛛机器人如同排球大小,“腹部”底盘较低,并且安装了驱动风扇.假设所攀爬的墙体为一张纸,当纸靠近运转的电风扇时,由于压力差的改变,纸会被紧紧吸附在电扇表面.正是运用了这个原理,当机器人腹部的驱动风扇开始运转,它便可以稳稳地吸附于墙体上.假设“蜘蛛侠”在竖直玻璃墙面上由A点沿直线匀加速“爬行”到B点.在此过程中,重力之外的其他力的合力用F表示,则对“蜘蛛侠”受力情况分析正确的是( )
2.(生活情境)“儿童蹦极”中,拴在腰间左右两侧的是弹性橡皮绳.质量为m的小丽如图所示静止悬挂时,两橡皮绳的拉力大小均恰为mg,若此时小丽左侧橡皮绳断裂,则小丽此时的( )
A.加速度为零
B.加速度a=g,沿断裂橡皮绳的方向斜向下
C.加速度a=g,沿未断裂橡皮绳的方向斜向上
D.加速度a=g,方向竖直向下
3.如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=2 kg的无人机,能提供向上的最大升力为32 N.现让无人机在地面上从静止开始竖直向上运动,25 s后悬停在空中,执行拍摄任务.前25 s内运动的v-t图像如图所示,在运动时所受阻力大小恒为无人机重力的0.2倍,g取10 m/s2.求:
(1)从静止开始竖直向上运动,25秒内运动的位移大小;
(2)加速和减速上升过程中提供的升力;
(3)25 s后悬停在空中,完成拍摄任务后,关闭升力一段时间,之后又重新启动提供向上最大升力.为保证安全着地,求无人机从开始下落到恢复升力的最长时间t(设无人机只做直线下落).
4.如图甲所示,停放在水平冰面上的冰车由质量为M,倾角为θ的斜面改装而成,在斜面上轻放一质量为m的物块,不计物块与斜面、冰车与冰面之间的摩擦.释放物块后,在物块沿斜面向下运动的同时,冰车也在水平面上运动,此时冰车受力的示意图如图乙所示,冰车在水平方向的合力作用下由静止变为运动,且在物块滑离斜面前沿冰面做加速运动.若冰面上的人在车后方用水平方向的力F推车,试分析冰车的运动情况有几种可能?并试分析特殊情况下,水平推力F和物块加速度a的大小分别是多少?
第3节 牛顿第二定律
必备知识基础练
1.解析:根据牛顿第二定律F=ma可知,加速度与合力是瞬时对应的关系,合力变化,加速度同时随之变化,当力刚开始作用的瞬间,物体所受的合力立即增大,则立即获得了加速度,而物体由于具有惯性,速度还没有改变,故B正确.
答案:B
2.
解析:小车向右做匀加速直线运动,物块M相对小车静止,加速度与车的加速度相同,以物块为研究对象,受力分析如图所示,对物块,由牛顿第二定律得N=Ma,a增大,表明N增大,由牛顿第三定律可知,M对车厢壁的压力N′=N增大,物块受到的最大静摩擦力增大,物块不可能沿壁下滑,M仍相对车厢静止,在竖直方向,M所受合外力为零,由平衡条件得f=Mg,M所受的静摩擦力不变;M受到的合外力不为零,竖直方向的合力不变,水平方向的合力增大,所以车厢与M的相互作用力增大,故A、D错误,B、C正确.
答案:BC
3.解析:木块受力如图所示,在竖直方向有F支=Mg-Fsin α,根据牛顿第三定律可知木块对地面的压力F压=F支=Mg-Fsin α;
在水平方向,由牛顿第二定律得Fcos α-μ(Mg-Fsin α)=Ma,
解得加速度a=,故选D.
答案:D
4.解析:猫处于平衡状态,隔离猫进行受力分析,猫受重力、板对它的支持力及板对猫沿斜面向上的摩擦力,A错误,B正确;木板沿斜面加速下滑时,猫保持相对斜面的位置不变,即相对斜面静止,加速度为零.将木板和猫作为整体,根据牛顿第二定律有F合=2ma(a为木板的加速度),整体受到的合力的大小为猫和木板的重力沿斜面方向的分力的大小,即F合=3mgsin α,解得a=gsin α,方向沿斜面向下,C错误,D正确.
答案:BD
5.解析:弹簧伸长量为4 cm时,重物处于平衡状态,故mg=kΔx1;再将重物向下拉1 cm,则弹簧的伸长量变为Δx2=5 cm,在重物被释放瞬间,由牛顿第二定律可得kΔx2-mg=ma.由以上两式解得a=2.5 m/s2,故A正确.
答案:A
关键能力综合练
1.解析:牛顿第二定律中的力应理解为物体所受的合力.用一个力推桌子没有推动,是由于桌子所受推力、重力、地面的支持力与摩擦力的合力等于零,桌子的加速度为零,所以桌子仍静止,故选项D正确,选项A、B、C错误.
答案:D
2.解析:一开始,物体所受合力为F=10 N-5 N=5 N,方向向左.当F2由10 N逐渐减小,F也逐渐减小,当F2减小到5 N时,F的值变为0,随着F2的继续减小,F方向变为向右,从0逐渐增大,当F2变为0的时候,F变为最大5 N,由牛顿第二定律知,物体的加速度大小是先减小后增大,故C正确.
答案:C
3.解析:力F作用于甲物体时,F=m1a1
力F作用于乙物体时,F=m2a2
力F作用于甲、乙组成的整体时,F=(m1+m2)a3
联立解得a3=,故选项C正确.
答案:C
4.
解析:分别以A、B为研究对象,分析剪断细绳前和剪断细绳时的受力.剪断细绳前A、B静止,A球受三个力:绳子的拉力FT、重力mg和弹簧弹力F,B球受两个力:重力mg和弹簧弹力F′,如图甲.
A球:FT-mg-F=0
B球:F′-mg=0,F=F′
解得FT=2mg,F=F′=mg.
剪断细绳瞬间,绳的拉力消失,而弹簧瞬间形状不可改变,弹力不变.如图乙,A球受重力mg、弹簧弹力F,B球受重力mg和弹簧弹力F′.
A球:mg+F=maA
B球:F′-mg=maB
解得aA=2g,aB=0.
答案:C
5.解析:当弹簧测力计甲的示数变为8 N时,弹簧测力计乙的示数变为12 N,这时物块所受的合力为4 N.由牛顿第二定律F=ma得物块的加速度a==4 m/s2,故选项B正确.
答案:B
6.解析:假设右边的重物质量减少Δm,则右边的重物向上做匀加速运动,左边的重物向下做匀加速运动,它们的加速度大小a相同,绳子的拉力大小F相等.
对右边重物,根据牛顿第二定律得F-(m-Δm)g=(m-Δm)a
对左边重物,根据牛顿第二定律得mg-F=ma
联立解得a=·g=·g,根据上式知,Δm和a并非是线性化关系,故A、B错误;当Δm=m时,可得a=g,故C正确,D错误.
答案:C
7.
解析:小球受力如图,由牛顿第二定律得F合=mg·tan 30°=ma
a=gtan 30°=g
则FN==mg
故B、D正确.
答案:BD
8.
解析:没有剪断Ⅰ、Ⅱ时小球受力情况如图所示.在剪断Ⅰ的瞬间,由于小球的速度为0,绳Ⅱ上的力突变为0,则小球只受重力作用,加速度为g,选项A正确,C错误;若剪断Ⅱ,由于弹簧的弹力不能突变,F1与重力的合力大小仍等于F2,所以此时加速度为a=,方向水平向左,选项B正确,D错误.
答案:AB
9.
解析:小车静止时,小球处于平衡状态,则杆对球的弹力F=mg,方向竖直向上,故A、B错误.小车向右匀速运动时,小球处于平衡状态,则杆对球的弹力F=mg,方向竖直向上,故C正确.小球向右做匀加速运动时,小球具有向右的加速度,合力向右,小球受力如图所示,根据几何知识可知,F>mg,方向由合力的大小决定,可能沿杆向上,故D正确.
答案:CD
10.
解析:(1)分析木块的受力情况如图甲所示,木块受重力mg、支持力FN两个力作用,合外力大小为mgsin θ,根据牛顿第二定律得mgsin θ=ma1,所以a1=gsin θ=10×0.6 m/s2=6 m/s2.
(2)若斜面粗糙,木块的受力情况如图乙所示,建立直角坐标系.
在x轴方向上(沿斜面方向)
mgsin θ-Ff=ma2
在y轴方向上(垂直斜面方向)
FN=mgcos θ
又因为Ff=μFN
联立解得a2=2 m/s2
答案:(1)6 m/s2 (2)2 m/s2
学科素养升级练
1.解析:“蜘蛛侠”在竖直玻璃墙面上由A点沿直线匀加速“爬行”到B点,加速度从A指向B,根据牛顿第二定律可知,在竖直平面内“蜘蛛侠”的合力方向应该是从A指向B,结合平行四边形定则知F与mg的合力沿A到B方向,故C正确,A、B、D错误.
答案:C
2.解析:当小丽处于静止状态时,拉力F=mg,两橡皮绳之间的夹角为120°,若小丽左侧橡皮绳断裂,则小丽此时所受合力沿断裂橡皮绳的方向斜向下,由牛顿第二定律F=ma知mg=ma,a=g,故选项B正确.
答案:B
3.解析:(1)由v-t图线与t轴所围面积表示位移可得,无人机从静止开始竖直向上运动,25秒内运动的位移大小为70 m.
(2)由v-t图线的斜率表示加速度知,加速过程加速度大小为a1=0.8 m/s2,设加速过程升力为F1
由牛顿第二定律得F1-mg-0.2 mg=ma1
解得F1=25.6 N
减速过程中加速度大小为a2=0.4 m/s2,设减速过程升力为F2
由牛顿第二定律得mg+0.2 mg-F2=ma2,
解得F2=23.2 N
(3)设失去升力下降阶段加速度大小为a3,由牛顿第二定律得mg-0.2 mg=ma3
解得a3=8 m/s2,方向向下
恢复最大升力后加速度大小为a4,由牛顿第二定律得Fmax-mg+0.2 mg=ma4,
解得a4=8 m/s2,方向向上
根据对称性可知,应在下落过程的中间位置恢复升力
由=a3t2,得t= s
答案:(1)70 m (2)25.6 N 23.2 N (3) s
4.解析:四种可能.情况一:物块在斜面上滑动的同时冰车在冰面上保持静止;情况二:物块和斜面保持相对静止且一起向右加速运动;情况三:物块在斜面上滑动的同时冰车在冰面上向左运动;情况四:物块在斜面上滑动的同时冰车在冰面上向右运动.其中情况一、二为特殊情况,情况三、四为一般情况.
对于情况一:冰车的受力情况如图1所示,物块的受力情况如图2所示.由于冰车保持静止,对冰车由平衡条件有:F1=FN sin θ,对物块由牛顿第二定律有:mg sin θ=ma1,又FN=mg cos θ,联立以上各式解得:a1=g sin θ,F1=mg cos θsin θ;对于情况二:物块受力情况如图3所示.对物块由牛顿第二定律有:mg tan θ=ma2,对物块和冰车整体由牛顿第二定律有:F2=(M+m)a2,联立以上各式解得:a2=g tan θ,F2=(M+m)g tan θ.
答案:四种可能.特殊情况下:F1=mg cos θsin θ,a1=g sin θ或F2=(M+m)gtan θ,a2=gtan θ.
必备知识基础练 进阶训练第一层
知识点一 牛顿第二定律
1.对静止在光滑水平面上的物体施加一水平拉力,当力刚开始作用的瞬间( )
A.物体立即获得速度
B.物体立即获得加速度
C.物体同时获得速度和加速度
D.由于物体未来得及运动,所以速度和加速度都为零
2.(多选)如图所示,当小车水平向右加速运动时,物块M相对静止于车厢后竖直壁上.当小车的加速度增大时( )
A.M所受的静摩擦力增大 B.M对车厢的作用力增大
C.M仍相对车厢静止 D.M受到的合外力为零
3.如图所示,位于水平地面上的质量为M的木块,在方向与水平面成α角、大小为F的拉力作用下,沿水平地面做匀加速直线运动,若木块与地面间的动摩擦因数为μ,则木块的加速度为( )
A. B.
C. D.
4.(多选)如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的较长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时( )
A.猫有向上的加速度
B.猫处于平衡状态,板对猫有沿斜面向上的摩擦力
C.板的加速度大小为gsin α,方向沿斜面向下
D.板的加速度大小为gsin α,方向沿斜面向下
知识点二 力的单位
5.一轻弹簧上端固定,下端挂一重物,平衡时弹簧伸长了4 cm,再将重物向下拉1 cm,然后放手,则在释放瞬间重物的加速度是(g取10 m/s2)( )
A.2.5 m/s2 B.7.5 m/s2
C.10 m/s2 D.12.5 m/s2
关键能力综合练 进阶训练第二层
一、单项选择题
1.由牛顿第二定律知,无论怎样小的力都可以使物体产生加速度,可是当我们用一个力推桌子没有推动时是因为( )
A.牛顿第二定律不适用于静止的物体
B.桌子的加速度很小,速度增量很小,眼睛不易觉察到
C.推力小于摩擦力,加速度是负值
D.推力、重力、地面的支持力与摩擦力的合力等于零,桌子的加速度为零,所以桌子仍静止
2.如图所示,放在光滑水平面上的一个物体,同时受到两个水平方向力的作用,其中水平向右的力F1=5 N,水平向左的力F2=10 N,当F2由10 N逐渐减小到零的过程中,物体的加速度大小变化情况是( )
A.逐渐减小 B.逐渐增大
C.先减小后增大 D.先增大后减小
3.力F作用于甲物体(质量为m1)时产生的加速度为a1,此力作用于乙物体(质量为m2)时产生的加速度为a2,若将甲、乙两个物体合在一起,仍受此力的作用.则产生的加速度是( )
A. B.
C. D.
4.(探究题)如图所示,天花板上用细绳吊起两个用轻弹簧相连的质量相同的小球,两小球均保持静止.已知重力加速度为g,当突然剪断细绳时,上面的小球A与下面的小球B的加速度为( )
A.aA=g,aB=g B.aA=g,aB=0
C.aA=2g,aB=0 D.aA=0,aB=g
5.如图所示,底板光滑的小车上用两个量程为0~20 N、完全相同的弹簧测力计甲和乙系住一个质量为1 kg的物块.在水平地面上,当小车做匀速直线运动时,两弹簧测力计的示数均为10 N,当小车做匀加速直线运动时,弹簧测力计甲的示数变为8 N.这时小车运动的加速度大小是( )
A.2 m/s2 B.4 m/s2
C.6 m/s2 D.8 m/s2
6.早在公元前4世纪末,我国的《墨经》中就有关于力和运动的一些见解,如“绳下直,权重相若则正矣.收,上者愈丧,下者愈得”,这句话所描述的情况与下述物理现象相似.如图,一根跨过定滑轮的轻绳两端各悬挂一重物,当两重物质量均为m时,系统处于平衡状态.若减小其中一个重物的质量,系统就无法保持平衡,上升的重物减小的质量Δm越多,另一个重物下降的加速度a就越大.已知重力加速度为g,则a与Δm的关系图像可能是( )
二、多项选择题
7.半圆形光滑圆槽内放一质量为m的小球,今用外力拉着圆槽在水平面上做匀加速直线运动,稳定后小球位置如图所示,已知重力加速度为g,则小球受圆槽的支持力FN和加速度a为( )
A.FN=mg B.FN=mg
C.a=g D.a=g
8.(易错题)如图所示,质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q两点.小球静止时,Ⅰ中拉力的大小为F1,Ⅱ中拉力的大小为F2,当仅剪断Ⅰ、Ⅱ其中一根的瞬间,球的加速度a应是( )
A.若剪断Ⅰ,则a=g,方向竖直向下
B.若剪断Ⅱ,则a=,方向水平向左
C.若剪断Ⅰ,则a=,方向沿Ⅰ的延长线方向
D.若剪断Ⅱ,则a=g,方向竖直向上
9.如图所示为位于水平面上的小车,固定在小车上的支架斜杆与竖直杆的夹角为θ,在斜杆的下端固定有质量为m的小球.下列关于斜杆对球的作用力F的判断中,正确的是( )
A.小车静止时,F=mgsin θ,方向沿杆向上
B.小车静止时,F=mgcos θ,方向垂直于杆向上
C.小车向右做匀速运动时,一定有F=mg,方向竖直向上
D.小车向右做匀加速运动时,一定有F>mg,方向可能沿杆向上
三、非选择题
10.如图所示,一木块沿倾角θ=37°的光滑固定斜面自由下滑.g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求木块的加速度大小;
(2)若木块与斜面间的动摩擦因数μ=0.5,求木块加速度的大小.
学科素养升级练 进阶训练第三层
1.(学术情境)来自北京工业大学的一群大学生,受“蜘蛛侠”的启发,研发出了独特的六爪攀壁蜘蛛机器人(如图甲).六爪攀壁蜘蛛机器人如同排球大小,“腹部”底盘较低,并且安装了驱动风扇.假设所攀爬的墙体为一张纸,当纸靠近运转的电风扇时,由于压力差的改变,纸会被紧紧吸附在电扇表面.正是运用了这个原理,当机器人腹部的驱动风扇开始运转,它便可以稳稳地吸附于墙体上.假设“蜘蛛侠”在竖直玻璃墙面上由A点沿直线匀加速“爬行”到B点.在此过程中,重力之外的其他力的合力用F表示,则对“蜘蛛侠”受力情况分析正确的是( )
2.(生活情境)“儿童蹦极”中,拴在腰间左右两侧的是弹性橡皮绳.质量为m的小丽如图所示静止悬挂时,两橡皮绳的拉力大小均恰为mg,若此时小丽左侧橡皮绳断裂,则小丽此时的( )
A.加速度为零
B.加速度a=g,沿断裂橡皮绳的方向斜向下
C.加速度a=g,沿未断裂橡皮绳的方向斜向上
D.加速度a=g,方向竖直向下
3.如图所示为四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.一架质量m=2 kg的无人机,能提供向上的最大升力为32 N.现让无人机在地面上从静止开始竖直向上运动,25 s后悬停在空中,执行拍摄任务.前25 s内运动的v-t图像如图所示,在运动时所受阻力大小恒为无人机重力的0.2倍,g取10 m/s2.求:
(1)从静止开始竖直向上运动,25秒内运动的位移大小;
(2)加速和减速上升过程中提供的升力;
(3)25 s后悬停在空中,完成拍摄任务后,关闭升力一段时间,之后又重新启动提供向上最大升力.为保证安全着地,求无人机从开始下落到恢复升力的最长时间t(设无人机只做直线下落).
4.如图甲所示,停放在水平冰面上的冰车由质量为M,倾角为θ的斜面改装而成,在斜面上轻放一质量为m的物块,不计物块与斜面、冰车与冰面之间的摩擦.释放物块后,在物块沿斜面向下运动的同时,冰车也在水平面上运动,此时冰车受力的示意图如图乙所示,冰车在水平方向的合力作用下由静止变为运动,且在物块滑离斜面前沿冰面做加速运动.若冰面上的人在车后方用水平方向的力F推车,试分析冰车的运动情况有几种可能?并试分析特殊情况下,水平推力F和物块加速度a的大小分别是多少?
第3节 牛顿第二定律
必备知识基础练
1.解析:根据牛顿第二定律F=ma可知,加速度与合力是瞬时对应的关系,合力变化,加速度同时随之变化,当力刚开始作用的瞬间,物体所受的合力立即增大,则立即获得了加速度,而物体由于具有惯性,速度还没有改变,故B正确.
答案:B
2.
解析:小车向右做匀加速直线运动,物块M相对小车静止,加速度与车的加速度相同,以物块为研究对象,受力分析如图所示,对物块,由牛顿第二定律得N=Ma,a增大,表明N增大,由牛顿第三定律可知,M对车厢壁的压力N′=N增大,物块受到的最大静摩擦力增大,物块不可能沿壁下滑,M仍相对车厢静止,在竖直方向,M所受合外力为零,由平衡条件得f=Mg,M所受的静摩擦力不变;M受到的合外力不为零,竖直方向的合力不变,水平方向的合力增大,所以车厢与M的相互作用力增大,故A、D错误,B、C正确.
答案:BC
3.解析:木块受力如图所示,在竖直方向有F支=Mg-Fsin α,根据牛顿第三定律可知木块对地面的压力F压=F支=Mg-Fsin α;
在水平方向,由牛顿第二定律得Fcos α-μ(Mg-Fsin α)=Ma,
解得加速度a=,故选D.
答案:D
4.解析:猫处于平衡状态,隔离猫进行受力分析,猫受重力、板对它的支持力及板对猫沿斜面向上的摩擦力,A错误,B正确;木板沿斜面加速下滑时,猫保持相对斜面的位置不变,即相对斜面静止,加速度为零.将木板和猫作为整体,根据牛顿第二定律有F合=2ma(a为木板的加速度),整体受到的合力的大小为猫和木板的重力沿斜面方向的分力的大小,即F合=3mgsin α,解得a=gsin α,方向沿斜面向下,C错误,D正确.
答案:BD
5.解析:弹簧伸长量为4 cm时,重物处于平衡状态,故mg=kΔx1;再将重物向下拉1 cm,则弹簧的伸长量变为Δx2=5 cm,在重物被释放瞬间,由牛顿第二定律可得kΔx2-mg=ma.由以上两式解得a=2.5 m/s2,故A正确.
答案:A
关键能力综合练
1.解析:牛顿第二定律中的力应理解为物体所受的合力.用一个力推桌子没有推动,是由于桌子所受推力、重力、地面的支持力与摩擦力的合力等于零,桌子的加速度为零,所以桌子仍静止,故选项D正确,选项A、B、C错误.
答案:D
2.解析:一开始,物体所受合力为F=10 N-5 N=5 N,方向向左.当F2由10 N逐渐减小,F也逐渐减小,当F2减小到5 N时,F的值变为0,随着F2的继续减小,F方向变为向右,从0逐渐增大,当F2变为0的时候,F变为最大5 N,由牛顿第二定律知,物体的加速度大小是先减小后增大,故C正确.
答案:C
3.解析:力F作用于甲物体时,F=m1a1
力F作用于乙物体时,F=m2a2
力F作用于甲、乙组成的整体时,F=(m1+m2)a3
联立解得a3=,故选项C正确.
答案:C
4.
解析:分别以A、B为研究对象,分析剪断细绳前和剪断细绳时的受力.剪断细绳前A、B静止,A球受三个力:绳子的拉力FT、重力mg和弹簧弹力F,B球受两个力:重力mg和弹簧弹力F′,如图甲.
A球:FT-mg-F=0
B球:F′-mg=0,F=F′
解得FT=2mg,F=F′=mg.
剪断细绳瞬间,绳的拉力消失,而弹簧瞬间形状不可改变,弹力不变.如图乙,A球受重力mg、弹簧弹力F,B球受重力mg和弹簧弹力F′.
A球:mg+F=maA
B球:F′-mg=maB
解得aA=2g,aB=0.
答案:C
5.解析:当弹簧测力计甲的示数变为8 N时,弹簧测力计乙的示数变为12 N,这时物块所受的合力为4 N.由牛顿第二定律F=ma得物块的加速度a==4 m/s2,故选项B正确.
答案:B
6.解析:假设右边的重物质量减少Δm,则右边的重物向上做匀加速运动,左边的重物向下做匀加速运动,它们的加速度大小a相同,绳子的拉力大小F相等.
对右边重物,根据牛顿第二定律得F-(m-Δm)g=(m-Δm)a
对左边重物,根据牛顿第二定律得mg-F=ma
联立解得a=·g=·g,根据上式知,Δm和a并非是线性化关系,故A、B错误;当Δm=m时,可得a=g,故C正确,D错误.
答案:C
7.
解析:小球受力如图,由牛顿第二定律得F合=mg·tan 30°=ma
a=gtan 30°=g
则FN==mg
故B、D正确.
答案:BD
8.
解析:没有剪断Ⅰ、Ⅱ时小球受力情况如图所示.在剪断Ⅰ的瞬间,由于小球的速度为0,绳Ⅱ上的力突变为0,则小球只受重力作用,加速度为g,选项A正确,C错误;若剪断Ⅱ,由于弹簧的弹力不能突变,F1与重力的合力大小仍等于F2,所以此时加速度为a=,方向水平向左,选项B正确,D错误.
答案:AB
9.
解析:小车静止时,小球处于平衡状态,则杆对球的弹力F=mg,方向竖直向上,故A、B错误.小车向右匀速运动时,小球处于平衡状态,则杆对球的弹力F=mg,方向竖直向上,故C正确.小球向右做匀加速运动时,小球具有向右的加速度,合力向右,小球受力如图所示,根据几何知识可知,F>mg,方向由合力的大小决定,可能沿杆向上,故D正确.
答案:CD
10.
解析:(1)分析木块的受力情况如图甲所示,木块受重力mg、支持力FN两个力作用,合外力大小为mgsin θ,根据牛顿第二定律得mgsin θ=ma1,所以a1=gsin θ=10×0.6 m/s2=6 m/s2.
(2)若斜面粗糙,木块的受力情况如图乙所示,建立直角坐标系.
在x轴方向上(沿斜面方向)
mgsin θ-Ff=ma2
在y轴方向上(垂直斜面方向)
FN=mgcos θ
又因为Ff=μFN
联立解得a2=2 m/s2
答案:(1)6 m/s2 (2)2 m/s2
学科素养升级练
1.解析:“蜘蛛侠”在竖直玻璃墙面上由A点沿直线匀加速“爬行”到B点,加速度从A指向B,根据牛顿第二定律可知,在竖直平面内“蜘蛛侠”的合力方向应该是从A指向B,结合平行四边形定则知F与mg的合力沿A到B方向,故C正确,A、B、D错误.
答案:C
2.解析:当小丽处于静止状态时,拉力F=mg,两橡皮绳之间的夹角为120°,若小丽左侧橡皮绳断裂,则小丽此时所受合力沿断裂橡皮绳的方向斜向下,由牛顿第二定律F=ma知mg=ma,a=g,故选项B正确.
答案:B
3.解析:(1)由v-t图线与t轴所围面积表示位移可得,无人机从静止开始竖直向上运动,25秒内运动的位移大小为70 m.
(2)由v-t图线的斜率表示加速度知,加速过程加速度大小为a1=0.8 m/s2,设加速过程升力为F1
由牛顿第二定律得F1-mg-0.2 mg=ma1
解得F1=25.6 N
减速过程中加速度大小为a2=0.4 m/s2,设减速过程升力为F2
由牛顿第二定律得mg+0.2 mg-F2=ma2,
解得F2=23.2 N
(3)设失去升力下降阶段加速度大小为a3,由牛顿第二定律得mg-0.2 mg=ma3
解得a3=8 m/s2,方向向下
恢复最大升力后加速度大小为a4,由牛顿第二定律得Fmax-mg+0.2 mg=ma4,
解得a4=8 m/s2,方向向上
根据对称性可知,应在下落过程的中间位置恢复升力
由=a3t2,得t= s
答案:(1)70 m (2)25.6 N 23.2 N (3) s
4.解析:四种可能.情况一:物块在斜面上滑动的同时冰车在冰面上保持静止;情况二:物块和斜面保持相对静止且一起向右加速运动;情况三:物块在斜面上滑动的同时冰车在冰面上向左运动;情况四:物块在斜面上滑动的同时冰车在冰面上向右运动.其中情况一、二为特殊情况,情况三、四为一般情况.
对于情况一:冰车的受力情况如图1所示,物块的受力情况如图2所示.由于冰车保持静止,对冰车由平衡条件有:F1=FN sin θ,对物块由牛顿第二定律有:mg sin θ=ma1,又FN=mg cos θ,联立以上各式解得:a1=g sin θ,F1=mg cos θsin θ;对于情况二:物块受力情况如图3所示.对物块由牛顿第二定律有:mg tan θ=ma2,对物块和冰车整体由牛顿第二定律有:F2=(M+m)a2,联立以上各式解得:a2=g tan θ,F2=(M+m)g tan θ.
答案:四种可能.特殊情况下:F1=mg cos θsin θ,a1=g sin θ或F2=(M+m)gtan θ,a2=gtan θ.
