2011-2012学年八年级数学(人教版上)同步练习第十二章第二节作轴对称图形
文档属性
| 名称 | 2011-2012学年八年级数学(人教版上)同步练习第十二章第二节作轴对称图形 |  | |
| 格式 | zip | ||
| 文件大小 | 80.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-01 07:31:56 | ||
图片预览



文档简介
2011-2012学年八年级数学(人教版上)同步练习第十二章
第二节 作轴对称图形
一、 教学内容:
1. 基本概念:轴对称、轴对称图形,线段的垂直平分线。
2. 轴对称的性质。
3. 线段的垂直平分线的性质及判定
4. 尺规作图:轴对称图形的作法;作线段的垂直平分线
5. 关于坐标轴对称的点的坐标特点。
二、 知识要点:
1. 基本概念
(1)轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。 这时,我们也说这个图形关于这条直线(成轴)对称。
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
(3)轴对称和轴对称图形的区别和联系:
区别:①轴对称图形说的是一个具有特殊形状的图形;轴对称说的是两个图形的一种特殊位置关系。 ②轴对称是对两个图形说的,而轴对称图形是对一个图形说的。
联系:①都沿某条直线对折,图形重合。 ②如把两个成轴对称的图形看成一个整体,那么它就是一个轴对称图形;反过来,把轴对称图形的两部分分别看作两个图形,那么这两个图形成轴对称。
(4)线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
2. 轴对称的性质:
(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
(2)关于某条直线成轴对称的两个图形是全等图形。
轴对称图形的性质:(轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。)
3. 线段的垂直平分线的性质及判定
(1)线段垂直平分线上的点与这条线段两个端点的距离相等。
如图①,若PC是线段AB的垂直平分线(AC=BC,PC⊥AB),则PA=PB
(2)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
如图②,若PA=PB,则点P在线段AB的垂直平分线上。
4. 尺规作图
(1)如何作轴对称图形
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形;对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形。 所以作轴对称图形的关键是作点关于直线的对称点
(2)作线段的垂直平分线
① 分别以点A、B为圆心,以大于AB的长为半径作弧,两弧交于C、D两点,② 作直线CD。
CD就是线段AB的垂直平分线。
5. 关于坐标轴对称的点的坐标特点
点(x,y)关于x轴对称的点的坐标为(_____,_____);
点(x,y)关于y轴对称的点的坐标为(_____,_____)。
三、 重点难点:
1. 重点:①轴对称图形的性质;②线段垂直平分线的性质及判定;③关于坐标轴对称的点的坐标特点。
2. 难点:轴对称图形以及关于坐标轴对称的点的坐标特点。
【考点分析】
中考对本节内容考查的热点有轴对称图形的概念和性质,以及用轴对称、平移等知识设计图案。 试题的难度较小,以基础题为主,题型以填空题、选择题为主,也有简单的作图题。
【典型例题】
例1. 如图是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,有几种移法?(至少画四种,相同类型的算一种),怎样移动才能使所构成的图形具有尽可能多的对称轴?
分析:每个等边三角形都是轴对称图形,都有三条对称轴。 要使两个等边三角形组合的图形仍是轴对称图形,则它们至少有一条对称轴重合,要使组合后的图形的对称轴尽可能多,则要让这两个等边三角形的三条对称轴都重合。
解:不是。 有以下几种移动方法(如图所示),其中,第3个图的对称轴最多。
评析:看似没有规律的题目,其实往往蕴含着规律,我们要善于发现其中的内在规律,这样解题才不盲目。
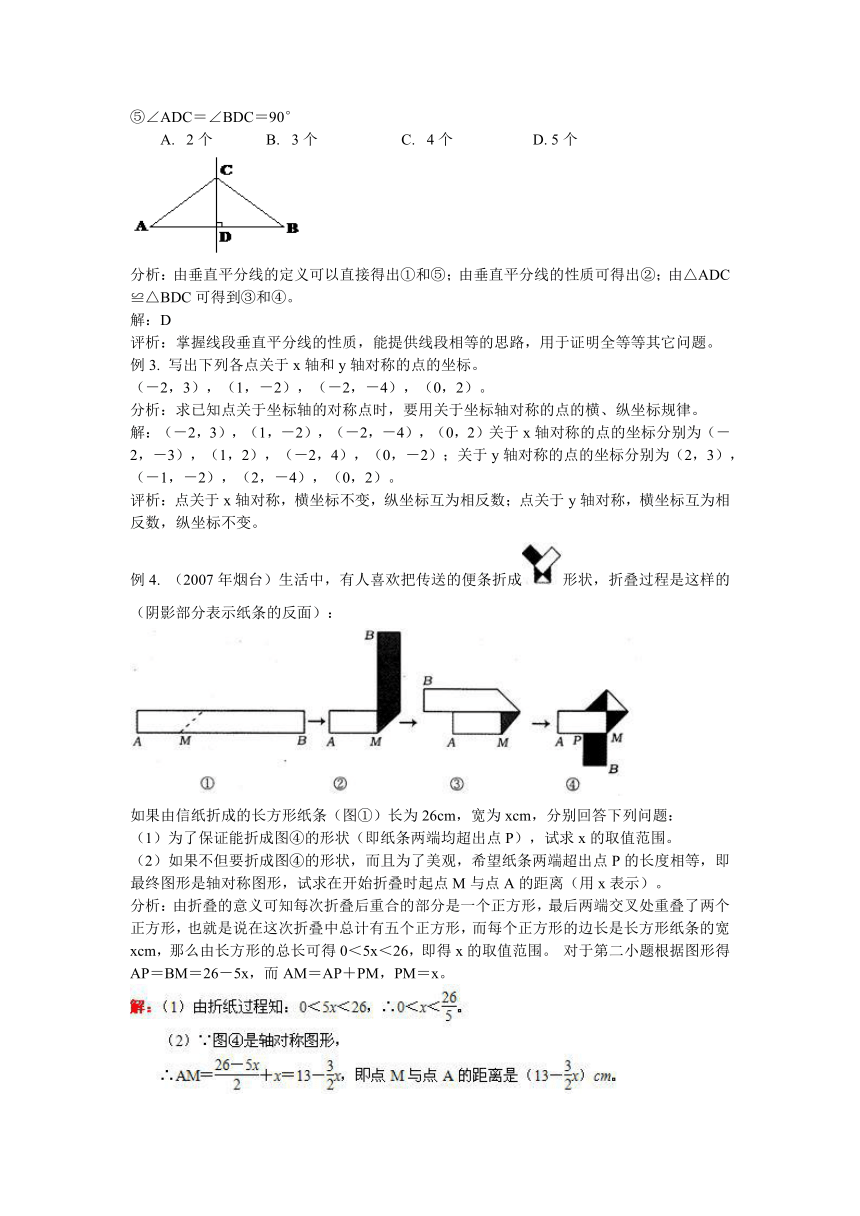
例2. 如图所示,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论中正确的有( )
①AD=BD; ②AC=BC; ③∠A=∠B; ④∠ACD=∠BCD;
⑤∠ADC=∠BDC=90°
A. 2个 B. 3个 C. 4个 D. 5个
分析:由垂直平分线的定义可以直接得出①和⑤;由垂直平分线的性质可得出②;由△ADC≌△BDC可得到③和④。
解:D
评析:掌握线段垂直平分线的性质,能提供线段相等的思路,用于证明全等等其它问题。
例3. 写出下列各点关于x轴和y轴对称的点的坐标。
(-2,3),(1,-2),(-2,-4),(0,2)。
分析:求已知点关于坐标轴的对称点时,要用关于坐标轴对称的点的横、纵坐标规律。
解:(-2,3),(1,-2),(-2,-4),(0,2)关于x轴对称的点的坐标分别为(-2,-3),(1,2),(-2,4),(0,-2);关于y轴对称的点的坐标分别为(2,3),(-1,-2),(2,-4),(0,2)。
评析:点关于x轴对称,横坐标不变,纵坐标互为相反数;点关于y轴对称,横坐标互为相反数,纵坐标不变。
例4. (2007年烟台)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围。
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示)。
分析:由折叠的意义可知每次折叠后重合的部分是一个正方形,最后两端交叉处重叠了两个正方形,也就是说在这次折叠中总计有五个正方形,而每个正方形的边长是长方形纸条的宽xcm,那么由长方形的总长可得0<5x<26,即得x的取值范围。 对于第二小题根据图形得AP=BM=26-5x,而AM=AP+PM,PM=x。
评析:图形的折叠问题是要弄清折叠后有哪些条件可用,并利用好折叠后图形的轴对称性与三角形全等等一些重要性质,本题中的折纸关键是要注意到所折角度应为45°,由①到④时长方形的长至少不少于宽的5倍。
例5. 如图所示,已知线段AB,画出线段AB关于直线l的对称图形。
分析:如果图形是由直线、射线或线段组成时,只要画出图形中的特殊点(如线段的端点、角的顶点等)的对称点,然后连结对称点,就可以画出对称图形。
解:(1)画出点A关于直线l的对称点A';
(2)画出点B关于直线l的对称点B':
(3)连结A'B',则线段A'B'即为所求。
评析:画已知图形关于某直线的对称图形:①对称轴是对应点连线的垂直平分线,②若对应线段或延长线相交,则交点一定在对称轴上。
例6. 要在河边修建一个水泵站,分别向张村、李庄送水(如图)。 修在河边什么地方,可使所用水管最短?
分析:在河岸l上找一点C,使AC+BC最短,利用轴对称把A点或B点变换到l的另一侧,而不改变路径的总长度,从而利用“两点之间,线段最短”使问题得到解决。
解:设张村为点A,李庄为点B,张村和李庄这一侧的河岸为直线l。
(1)作点B关于直线l的对称点,
(2)连结,交直线l于点C,
点C就是所求的水泵站的位置。 (如图所示)
评析:此类最小值问题解决的方法是:作出其中某一点关于直线的对称点,连接对称点与另一点的连线的交点,即是所求作的点。 依据是利用垂直平分线性质转移线段,利用两点之间线段最短得最短距离。
【方法总结】
本节从生活中的图形入手,学习图形的对称及其基本性质,欣赏、体验对称在现实生活中的广泛应用。 在此基础上,利用对称探索几何图形的性质,培养空间理解能力。 在解决实际问题时,要看透其中所包含的几何问题,把我们所掌握的轴对称和线段垂直平分线的知识转化为数学问题。
【模拟试题】(答题时间:40分钟)
一、 选择题
1. 下列说法错误的是 ( )
A. 关于某直线对称的两个图形一定能完全重合
B. 全等的两个三角形一定关于某直线对称
C. 轴对称图形的对称轴至少有一条
D. 线段是轴对称图形
2. 轴对称图形的对称轴是 ( )
A. 直线 B. 线段 C. 射线 D. 以上都有可能
3. 下面各组点关于y轴对称的是 ( )
A. (0,10)与(0,-10) B. (-3,-2)与(3,-2)
C. (-3,-2)与(3,2) D. (-3,-2)与(-3,2)
*4. 下列图形中,不是轴对称图形的是 ( )
A. 一条线段 B. 两条相交直线
C. 有公共端点的两条相等的线段 D. 有公共端点的两条不相等的线段
5. (2007年河南)如图,ΔABC与ΔA'B'C'关于直线l对称,则∠B的度数为 ( )
A. 30° B. 50° C. 90° D. 100°
6. (2008年江苏苏州)下列图形中,是轴对称图形的是 ( )
*7. (2008年武汉)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是 ( )
A. 150° B. 300° C. 210° D. 330°
**8. (2008年全国数学竞赛浙江预赛)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。 小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……,如此继续,得到一系列点P1,P2,P3,…,。 若与P重合,则n的最小值是 ( )
A. 5 B. 6 C. 7 D. 8
二、 填空题
9. (2006年宜昌)从汽车的后视镜中看见某车车牌的后5位号码是,该车牌的后5位号码实际是__________。
10. 如图所示,是用笔尖扎重叠的纸得到成轴对称的图案,请根据图形写出:
(1)两组对应点__________和__________;
(2)两组对应线段__________和__________;
(3)两组对应角__________和__________。
11. 点A(-5,-6)与点B(5,-6)关于__________对称。
*12.(2007年四川内江)已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=__________,n=__________。
三、 解答题
13. 画出下列各图形的所有对称轴。
14. 如图所示,作出△ABC关于直线l的对称三角形A'B'C'。
**15. (1)回答问题:①到线段两端点的距离相等的点在__________上;②到角的两边距离相等的点在__________上。
(2)根据(1)中的结论作图。
如图所示,求作一点P,使PC=PD,且使点P到∠AOB的两边的距离相等。
**16. 如图所示,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长。
四、 应用与探究题
17. 观察下图中的图形,虚线是不是它们的对称轴?你是如何验证的?
**18. 如图,草原上两个居民点A、B在河流l的同侧,一辆汽车从A出发到B,途中需到河边加水,汽车在哪一点加水,可使行驶的路程最短?
【试题答案】
一、 选择题
1. B 2. A 3. B 4。 D 5。 D 6。 D 7。 B 8。 B
二、 填空题
9. BA629
10. 答案不唯一,(1)A与D,B与E(2)AB与DE,AC与DF(3)∠A与∠D,∠B与∠E
11. y轴 12. 3,-4
三、 解答题
13. 如图所示:
14. 如图所示:
15. (1)①这条线段的垂直平分线;②这个角的平分线。 (2)①连结CD,②作线段CD的垂直平分线a,③作∠AOB的平分线OM,OM交a于点P。 点P就是所求作的点。
16. 解:∵DE垂直平分线段AB,∴DA=DB,AE=BE。 ∵AE=5cm,∴BE=5cm,∴AB=AE+BE=10cm。 ∵△ABC的周长=CA+CD+DB+AB,△ACD的周长=CA+CD+AD=CA+CD+DB=17cm,∴△ABC的周长=17+10=27cm。
四、 应用与探究题
17. 将这些图形分别沿图中的虚线对折,如果折叠后两边能够完全重合,那么这个图形就是轴对称图形,这条虚线就是它的对称轴;如果折叠后两边不能够完全重合,那么这条虚线就不是它的对称轴(不一定不是轴对称图形,如图(2)不是轴对称图形,图(3)是轴对称图形)。 用上述方法验证得:图(1)和(3)中的虚线是它们各自的对称轴,图(2)和(4)中的虚线不是它们各自的对称轴。
18. 如图所示,①作点B关于直线l的对称点,②连结,交直线l于点C. 点C就是所求的点。
第二节 作轴对称图形
一、 教学内容:
1. 基本概念:轴对称、轴对称图形,线段的垂直平分线。
2. 轴对称的性质。
3. 线段的垂直平分线的性质及判定
4. 尺规作图:轴对称图形的作法;作线段的垂直平分线
5. 关于坐标轴对称的点的坐标特点。
二、 知识要点:
1. 基本概念
(1)轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。 这时,我们也说这个图形关于这条直线(成轴)对称。
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
(3)轴对称和轴对称图形的区别和联系:
区别:①轴对称图形说的是一个具有特殊形状的图形;轴对称说的是两个图形的一种特殊位置关系。 ②轴对称是对两个图形说的,而轴对称图形是对一个图形说的。
联系:①都沿某条直线对折,图形重合。 ②如把两个成轴对称的图形看成一个整体,那么它就是一个轴对称图形;反过来,把轴对称图形的两部分分别看作两个图形,那么这两个图形成轴对称。
(4)线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
2. 轴对称的性质:
(1)如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
(2)关于某条直线成轴对称的两个图形是全等图形。
轴对称图形的性质:(轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。)
3. 线段的垂直平分线的性质及判定
(1)线段垂直平分线上的点与这条线段两个端点的距离相等。
如图①,若PC是线段AB的垂直平分线(AC=BC,PC⊥AB),则PA=PB
(2)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
如图②,若PA=PB,则点P在线段AB的垂直平分线上。
4. 尺规作图
(1)如何作轴对称图形
几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形;对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形。 所以作轴对称图形的关键是作点关于直线的对称点
(2)作线段的垂直平分线
① 分别以点A、B为圆心,以大于AB的长为半径作弧,两弧交于C、D两点,② 作直线CD。
CD就是线段AB的垂直平分线。
5. 关于坐标轴对称的点的坐标特点
点(x,y)关于x轴对称的点的坐标为(_____,_____);
点(x,y)关于y轴对称的点的坐标为(_____,_____)。
三、 重点难点:
1. 重点:①轴对称图形的性质;②线段垂直平分线的性质及判定;③关于坐标轴对称的点的坐标特点。
2. 难点:轴对称图形以及关于坐标轴对称的点的坐标特点。
【考点分析】
中考对本节内容考查的热点有轴对称图形的概念和性质,以及用轴对称、平移等知识设计图案。 试题的难度较小,以基础题为主,题型以填空题、选择题为主,也有简单的作图题。
【典型例题】
例1. 如图是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,有几种移法?(至少画四种,相同类型的算一种),怎样移动才能使所构成的图形具有尽可能多的对称轴?
分析:每个等边三角形都是轴对称图形,都有三条对称轴。 要使两个等边三角形组合的图形仍是轴对称图形,则它们至少有一条对称轴重合,要使组合后的图形的对称轴尽可能多,则要让这两个等边三角形的三条对称轴都重合。
解:不是。 有以下几种移动方法(如图所示),其中,第3个图的对称轴最多。
评析:看似没有规律的题目,其实往往蕴含着规律,我们要善于发现其中的内在规律,这样解题才不盲目。
例2. 如图所示,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论中正确的有( )
①AD=BD; ②AC=BC; ③∠A=∠B; ④∠ACD=∠BCD;
⑤∠ADC=∠BDC=90°
A. 2个 B. 3个 C. 4个 D. 5个
分析:由垂直平分线的定义可以直接得出①和⑤;由垂直平分线的性质可得出②;由△ADC≌△BDC可得到③和④。
解:D
评析:掌握线段垂直平分线的性质,能提供线段相等的思路,用于证明全等等其它问题。
例3. 写出下列各点关于x轴和y轴对称的点的坐标。
(-2,3),(1,-2),(-2,-4),(0,2)。
分析:求已知点关于坐标轴的对称点时,要用关于坐标轴对称的点的横、纵坐标规律。
解:(-2,3),(1,-2),(-2,-4),(0,2)关于x轴对称的点的坐标分别为(-2,-3),(1,2),(-2,4),(0,-2);关于y轴对称的点的坐标分别为(2,3),(-1,-2),(2,-4),(0,2)。
评析:点关于x轴对称,横坐标不变,纵坐标互为相反数;点关于y轴对称,横坐标互为相反数,纵坐标不变。
例4. (2007年烟台)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为26cm,宽为xcm,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围。
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示)。
分析:由折叠的意义可知每次折叠后重合的部分是一个正方形,最后两端交叉处重叠了两个正方形,也就是说在这次折叠中总计有五个正方形,而每个正方形的边长是长方形纸条的宽xcm,那么由长方形的总长可得0<5x<26,即得x的取值范围。 对于第二小题根据图形得AP=BM=26-5x,而AM=AP+PM,PM=x。
评析:图形的折叠问题是要弄清折叠后有哪些条件可用,并利用好折叠后图形的轴对称性与三角形全等等一些重要性质,本题中的折纸关键是要注意到所折角度应为45°,由①到④时长方形的长至少不少于宽的5倍。
例5. 如图所示,已知线段AB,画出线段AB关于直线l的对称图形。
分析:如果图形是由直线、射线或线段组成时,只要画出图形中的特殊点(如线段的端点、角的顶点等)的对称点,然后连结对称点,就可以画出对称图形。
解:(1)画出点A关于直线l的对称点A';
(2)画出点B关于直线l的对称点B':
(3)连结A'B',则线段A'B'即为所求。
评析:画已知图形关于某直线的对称图形:①对称轴是对应点连线的垂直平分线,②若对应线段或延长线相交,则交点一定在对称轴上。
例6. 要在河边修建一个水泵站,分别向张村、李庄送水(如图)。 修在河边什么地方,可使所用水管最短?
分析:在河岸l上找一点C,使AC+BC最短,利用轴对称把A点或B点变换到l的另一侧,而不改变路径的总长度,从而利用“两点之间,线段最短”使问题得到解决。
解:设张村为点A,李庄为点B,张村和李庄这一侧的河岸为直线l。
(1)作点B关于直线l的对称点,
(2)连结,交直线l于点C,
点C就是所求的水泵站的位置。 (如图所示)
评析:此类最小值问题解决的方法是:作出其中某一点关于直线的对称点,连接对称点与另一点的连线的交点,即是所求作的点。 依据是利用垂直平分线性质转移线段,利用两点之间线段最短得最短距离。
【方法总结】
本节从生活中的图形入手,学习图形的对称及其基本性质,欣赏、体验对称在现实生活中的广泛应用。 在此基础上,利用对称探索几何图形的性质,培养空间理解能力。 在解决实际问题时,要看透其中所包含的几何问题,把我们所掌握的轴对称和线段垂直平分线的知识转化为数学问题。
【模拟试题】(答题时间:40分钟)
一、 选择题
1. 下列说法错误的是 ( )
A. 关于某直线对称的两个图形一定能完全重合
B. 全等的两个三角形一定关于某直线对称
C. 轴对称图形的对称轴至少有一条
D. 线段是轴对称图形
2. 轴对称图形的对称轴是 ( )
A. 直线 B. 线段 C. 射线 D. 以上都有可能
3. 下面各组点关于y轴对称的是 ( )
A. (0,10)与(0,-10) B. (-3,-2)与(3,-2)
C. (-3,-2)与(3,2) D. (-3,-2)与(-3,2)
*4. 下列图形中,不是轴对称图形的是 ( )
A. 一条线段 B. 两条相交直线
C. 有公共端点的两条相等的线段 D. 有公共端点的两条不相等的线段
5. (2007年河南)如图,ΔABC与ΔA'B'C'关于直线l对称,则∠B的度数为 ( )
A. 30° B. 50° C. 90° D. 100°
6. (2008年江苏苏州)下列图形中,是轴对称图形的是 ( )
*7. (2008年武汉)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是 ( )
A. 150° B. 300° C. 210° D. 330°
**8. (2008年全国数学竞赛浙江预赛)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。 小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……,如此继续,得到一系列点P1,P2,P3,…,。 若与P重合,则n的最小值是 ( )
A. 5 B. 6 C. 7 D. 8
二、 填空题
9. (2006年宜昌)从汽车的后视镜中看见某车车牌的后5位号码是,该车牌的后5位号码实际是__________。
10. 如图所示,是用笔尖扎重叠的纸得到成轴对称的图案,请根据图形写出:
(1)两组对应点__________和__________;
(2)两组对应线段__________和__________;
(3)两组对应角__________和__________。
11. 点A(-5,-6)与点B(5,-6)关于__________对称。
*12.(2007年四川内江)已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=__________,n=__________。
三、 解答题
13. 画出下列各图形的所有对称轴。
14. 如图所示,作出△ABC关于直线l的对称三角形A'B'C'。
**15. (1)回答问题:①到线段两端点的距离相等的点在__________上;②到角的两边距离相等的点在__________上。
(2)根据(1)中的结论作图。
如图所示,求作一点P,使PC=PD,且使点P到∠AOB的两边的距离相等。
**16. 如图所示,△ABC中,DE垂直平分线段AB,AE=5cm,△ACD的周长为17cm,求△ABC的周长。
四、 应用与探究题
17. 观察下图中的图形,虚线是不是它们的对称轴?你是如何验证的?
**18. 如图,草原上两个居民点A、B在河流l的同侧,一辆汽车从A出发到B,途中需到河边加水,汽车在哪一点加水,可使行驶的路程最短?
【试题答案】
一、 选择题
1. B 2. A 3. B 4。 D 5。 D 6。 D 7。 B 8。 B
二、 填空题
9. BA629
10. 答案不唯一,(1)A与D,B与E(2)AB与DE,AC与DF(3)∠A与∠D,∠B与∠E
11. y轴 12. 3,-4
三、 解答题
13. 如图所示:
14. 如图所示:
15. (1)①这条线段的垂直平分线;②这个角的平分线。 (2)①连结CD,②作线段CD的垂直平分线a,③作∠AOB的平分线OM,OM交a于点P。 点P就是所求作的点。
16. 解:∵DE垂直平分线段AB,∴DA=DB,AE=BE。 ∵AE=5cm,∴BE=5cm,∴AB=AE+BE=10cm。 ∵△ABC的周长=CA+CD+DB+AB,△ACD的周长=CA+CD+AD=CA+CD+DB=17cm,∴△ABC的周长=17+10=27cm。
四、 应用与探究题
17. 将这些图形分别沿图中的虚线对折,如果折叠后两边能够完全重合,那么这个图形就是轴对称图形,这条虚线就是它的对称轴;如果折叠后两边不能够完全重合,那么这条虚线就不是它的对称轴(不一定不是轴对称图形,如图(2)不是轴对称图形,图(3)是轴对称图形)。 用上述方法验证得:图(1)和(3)中的虚线是它们各自的对称轴,图(2)和(4)中的虚线不是它们各自的对称轴。
18. 如图所示,①作点B关于直线l的对称点,②连结,交直线l于点C. 点C就是所求的点。
