2011-2012学年八年级数学(人教版上)同步练习第十二章第三节等腰三角形
文档属性
| 名称 | 2011-2012学年八年级数学(人教版上)同步练习第十二章第三节等腰三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 65.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-01 00:00:00 | ||
图片预览

文档简介
2011-2012学年八年级数学(人教版上)同步练习第十二章
第三节 等腰三角形
一. 教学内容:
等腰三角形及其性质
二. 教学重点:
等腰三角形的性质和判定
三. 教学难点:
利用等腰三角形的性质定理和判定定理证明和计算
【典型例题】
[例1] 如图,在△ABC中,D是AB边上一点,AD=DC,∠B=,∠ACD=,求:∠BCD的度数
答案:
解析:因为AD=DC,所以∠A=∠ACD,又因为∠ACD=,所以∠A=,因为∠B=,利用三角形内角和定理,得到∠ACB=,所以∠BCD=∠ACB-∠ACD=
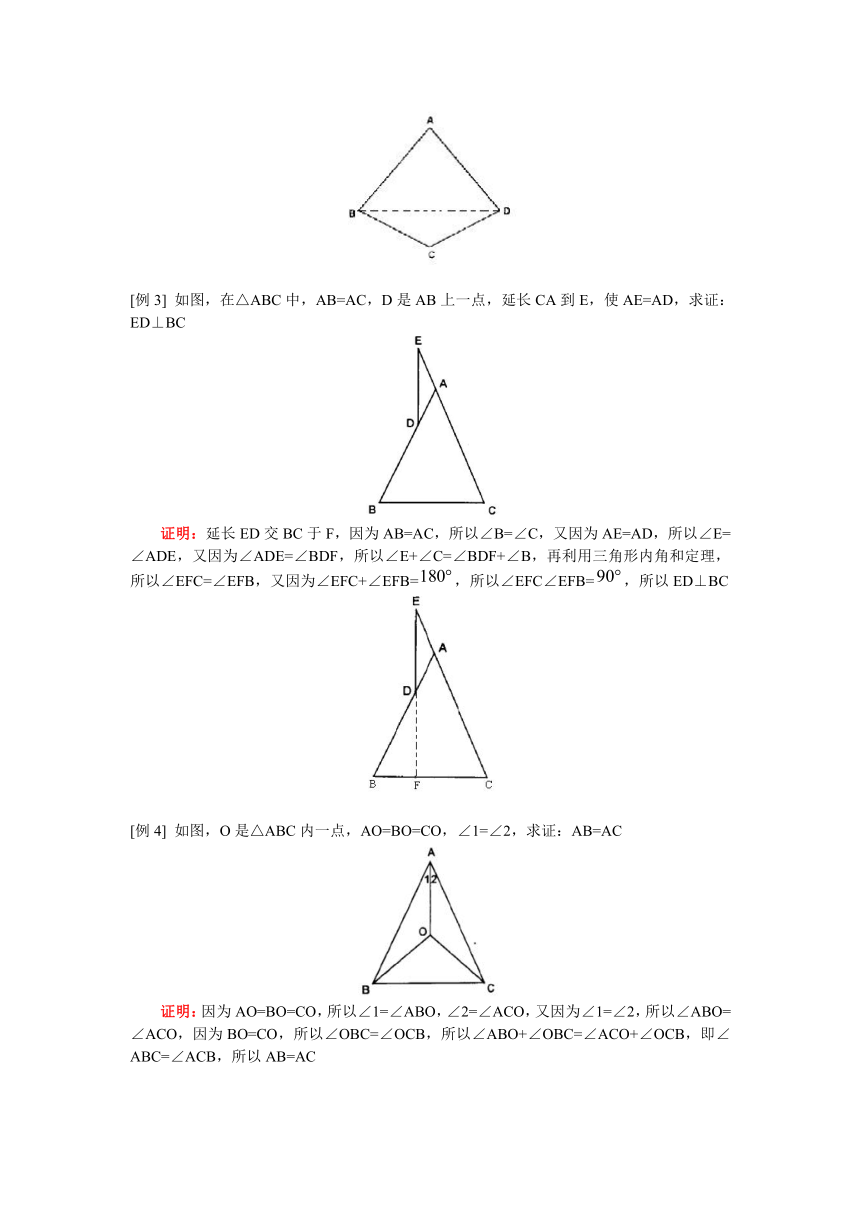
[例2] 如图,四边形ABCD中,AB=AD,BC=DC,求证:∠ABC=∠ADC
答案:
解析:连结BD,因为AB=AD,所以△ABD是等腰三角形,所以∠ABD=∠ADB,又因为BC=DC,所以△BCD是等腰三角形,所以∠CBD=∠CDB,所以∠ABD+∠CBD=∠ADB+∠CDB,即∠ABC=∠ADC
[例3] 如图,在△ABC中,AB=AC,D是AB上一点,延长CA到E,使AE=AD,求证:ED⊥BC
证明:延长ED交BC于F,因为AB=AC,所以∠B=∠C,又因为AE=AD,所以∠E=∠ADE,又因为∠ADE=∠BDF,所以∠E+∠C=∠BDF+∠B,再利用三角形内角和定理,所以∠EFC=∠EFB,又因为∠EFC+∠EFB=,所以∠EFC∠EFB=,所以ED⊥BC
[例4] 如图,O是△ABC内一点,AO=BO=CO,∠1=∠2,求证:AB=AC
证明:因为AO=BO=CO,所以∠1=∠ABO,∠2=∠ACO,又因为∠1=∠2,所以∠ABO=∠ACO,因为BO=CO,所以∠OBC=∠OCB,所以∠ABO+∠OBC=∠ACO+∠OCB,即∠ABC=∠ACB,所以AB=AC
[例5] 如图,在△ABC中,AB=AC,AD⊥BC于D,且△ABC的周长为,△ABD的周长为,求:AD的长
答案:
解析:因为△ABC的周长为,所以AB+AC+BC=,又因为△ABD的周长为,所以AB+BD+AD=,又根据AB=AC,所以,再利用等腰三角形三线合一,所以得到,所以,这样就可以解出
[例6] 如图,∠ABC、∠ACB的平分线相交于点F,过F作DE∥BC交AB于D,交AC于E,求证:BD+EC=DE
证明:因为∠ABC、∠ACB的平分线相交于点F,所以∠DBF=∠FBC,且∠ECF=∠FCB,又因为DE∥BC,所以∠DFB=∠FBC,∠EFC=∠FCB,所以∠DBF=∠DFB,∠EFC=∠ECF,所以DF=DB,EF=EC,所以BD+EC=DF+EF,即BD+EC=DE
[例7] 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,求证:∠DBC=∠A
证明:作AE⊥BC于E,因为BD⊥AC,AE⊥BC,所以∠BDC=∠AEC=,根据三角形内角和定理,所以∠EAC+∠C=,∠DBC+∠C=,根据同角的余角相等,所以∠EAC=∠DBC,又因为AB=AC,根据等腰三角形三线合一,所以AE是∠BAC的角平分线,所以∠EAC=∠BAC,即∠DBC=∠A
[例8] 如图,AD是△ABC的角平分线,且AC=AB+BD,求证:∠B=2∠C
解析:作辅助线,延AB至E使AE=AC,因为AC=AB+BD,所以AE=AB+BD,又因为AE=AB=BE,所以BD=BE,所以∠E=∠BDE,因为AD是△ABC的角平分线,所以∠EAD=∠CAD,且AE=AC,AD=AD,所以△AED≌△ACD,所以∠C=∠E,根据外角定理,所以∠ABD=∠E+∠BDE,所以∠ABD=2∠E,所以得到∠ABE=2∠C,即∠B=2∠C
【模拟试题】
一. 选择题:
1. 等腰三角形的一个角是94°,则腰与底边上的高的夹角为( )
A. 43° B. 53° C. 47° D. 90°
2. 等腰三角形周长为13cm,其中一边长为3cm,则该等腰三角形底边长( )
A. 7cm B. 3cm C. 7cm或3cm D. 5cm
3. 等腰三角形的两个内角的比是1:2,则这个等腰三角形是( )
A. 锐角三角形 B. 直角三角形
C. 锐角三角形或直角三角形 D. 以上结论都不对
4. 已知等腰三角形的一个外角等于70°,则底角的度数为( )
A. 110° B. 55° C. 35° D. 不能确定
5. 等腰三角形一腰上的高与底边所成角为36°,这个等腰三角形的顶角为( )
A. 36° B. 72° C. 36°或72° D. 54°
二. 填空题:
1. 如果等腰三角形一个角是45°,那么另外两个角的度数为
2. 等腰三角形一个外角等于110°,则底角的度数是
3. 等腰三角形 互相重合
4. 等腰三角形底边长为10,则其腰长x的范围是
5. 等腰三角形的底边长为5,一腰上中线把这个三角形周长分为两部分,它们的差为3,则腰长为
三. 解答题:
1. 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,求证:AF⊥CD
2. 如图,CE、CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D,求证:DE=DF
【试题答案】
一.
1. C 2. B 3. C 4. C 5. B
二.
1. 45°和90°或67.5°和67.5°
2. 70°或55°
3. 顶角角平分线和底边中线和底边高线
4. 大于5
5. 8
三.
1. 连结AC和AD,证明△ABC≌△AED,得到AC=AD,再利用等腰三角形三线合一
2. 分别证明DE=DC,DF=DC,所以DE=DF
第三节 等腰三角形
一. 教学内容:
等腰三角形及其性质
二. 教学重点:
等腰三角形的性质和判定
三. 教学难点:
利用等腰三角形的性质定理和判定定理证明和计算
【典型例题】
[例1] 如图,在△ABC中,D是AB边上一点,AD=DC,∠B=,∠ACD=,求:∠BCD的度数
答案:
解析:因为AD=DC,所以∠A=∠ACD,又因为∠ACD=,所以∠A=,因为∠B=,利用三角形内角和定理,得到∠ACB=,所以∠BCD=∠ACB-∠ACD=
[例2] 如图,四边形ABCD中,AB=AD,BC=DC,求证:∠ABC=∠ADC
答案:
解析:连结BD,因为AB=AD,所以△ABD是等腰三角形,所以∠ABD=∠ADB,又因为BC=DC,所以△BCD是等腰三角形,所以∠CBD=∠CDB,所以∠ABD+∠CBD=∠ADB+∠CDB,即∠ABC=∠ADC
[例3] 如图,在△ABC中,AB=AC,D是AB上一点,延长CA到E,使AE=AD,求证:ED⊥BC
证明:延长ED交BC于F,因为AB=AC,所以∠B=∠C,又因为AE=AD,所以∠E=∠ADE,又因为∠ADE=∠BDF,所以∠E+∠C=∠BDF+∠B,再利用三角形内角和定理,所以∠EFC=∠EFB,又因为∠EFC+∠EFB=,所以∠EFC∠EFB=,所以ED⊥BC
[例4] 如图,O是△ABC内一点,AO=BO=CO,∠1=∠2,求证:AB=AC
证明:因为AO=BO=CO,所以∠1=∠ABO,∠2=∠ACO,又因为∠1=∠2,所以∠ABO=∠ACO,因为BO=CO,所以∠OBC=∠OCB,所以∠ABO+∠OBC=∠ACO+∠OCB,即∠ABC=∠ACB,所以AB=AC
[例5] 如图,在△ABC中,AB=AC,AD⊥BC于D,且△ABC的周长为,△ABD的周长为,求:AD的长
答案:
解析:因为△ABC的周长为,所以AB+AC+BC=,又因为△ABD的周长为,所以AB+BD+AD=,又根据AB=AC,所以,再利用等腰三角形三线合一,所以得到,所以,这样就可以解出
[例6] 如图,∠ABC、∠ACB的平分线相交于点F,过F作DE∥BC交AB于D,交AC于E,求证:BD+EC=DE
证明:因为∠ABC、∠ACB的平分线相交于点F,所以∠DBF=∠FBC,且∠ECF=∠FCB,又因为DE∥BC,所以∠DFB=∠FBC,∠EFC=∠FCB,所以∠DBF=∠DFB,∠EFC=∠ECF,所以DF=DB,EF=EC,所以BD+EC=DF+EF,即BD+EC=DE
[例7] 如图,在△ABC中,AB=AC,BD⊥AC,垂足为D,求证:∠DBC=∠A
证明:作AE⊥BC于E,因为BD⊥AC,AE⊥BC,所以∠BDC=∠AEC=,根据三角形内角和定理,所以∠EAC+∠C=,∠DBC+∠C=,根据同角的余角相等,所以∠EAC=∠DBC,又因为AB=AC,根据等腰三角形三线合一,所以AE是∠BAC的角平分线,所以∠EAC=∠BAC,即∠DBC=∠A
[例8] 如图,AD是△ABC的角平分线,且AC=AB+BD,求证:∠B=2∠C
解析:作辅助线,延AB至E使AE=AC,因为AC=AB+BD,所以AE=AB+BD,又因为AE=AB=BE,所以BD=BE,所以∠E=∠BDE,因为AD是△ABC的角平分线,所以∠EAD=∠CAD,且AE=AC,AD=AD,所以△AED≌△ACD,所以∠C=∠E,根据外角定理,所以∠ABD=∠E+∠BDE,所以∠ABD=2∠E,所以得到∠ABE=2∠C,即∠B=2∠C
【模拟试题】
一. 选择题:
1. 等腰三角形的一个角是94°,则腰与底边上的高的夹角为( )
A. 43° B. 53° C. 47° D. 90°
2. 等腰三角形周长为13cm,其中一边长为3cm,则该等腰三角形底边长( )
A. 7cm B. 3cm C. 7cm或3cm D. 5cm
3. 等腰三角形的两个内角的比是1:2,则这个等腰三角形是( )
A. 锐角三角形 B. 直角三角形
C. 锐角三角形或直角三角形 D. 以上结论都不对
4. 已知等腰三角形的一个外角等于70°,则底角的度数为( )
A. 110° B. 55° C. 35° D. 不能确定
5. 等腰三角形一腰上的高与底边所成角为36°,这个等腰三角形的顶角为( )
A. 36° B. 72° C. 36°或72° D. 54°
二. 填空题:
1. 如果等腰三角形一个角是45°,那么另外两个角的度数为
2. 等腰三角形一个外角等于110°,则底角的度数是
3. 等腰三角形 互相重合
4. 等腰三角形底边长为10,则其腰长x的范围是
5. 等腰三角形的底边长为5,一腰上中线把这个三角形周长分为两部分,它们的差为3,则腰长为
三. 解答题:
1. 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,求证:AF⊥CD
2. 如图,CE、CF分别平分∠ACB和∠ACB的外角,EF∥BC交AC于D,求证:DE=DF
【试题答案】
一.
1. C 2. B 3. C 4. C 5. B
二.
1. 45°和90°或67.5°和67.5°
2. 70°或55°
3. 顶角角平分线和底边中线和底边高线
4. 大于5
5. 8
三.
1. 连结AC和AD,证明△ABC≌△AED,得到AC=AD,再利用等腰三角形三线合一
2. 分别证明DE=DC,DF=DC,所以DE=DF
