六年级上册数学课件-3.8 比的基本性质和化简比苏教版 (共23张PPT)
文档属性
| 名称 | 六年级上册数学课件-3.8 比的基本性质和化简比苏教版 (共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 09:54:11 | ||
图片预览







文档简介
1、比值的定义
2、比、除法、分数三者关系
3、我们学过哪些基本性质?
13
18
13
18
13÷18 = =( )∶( )
( )
( )
( )
( )
( )
一、复习准备
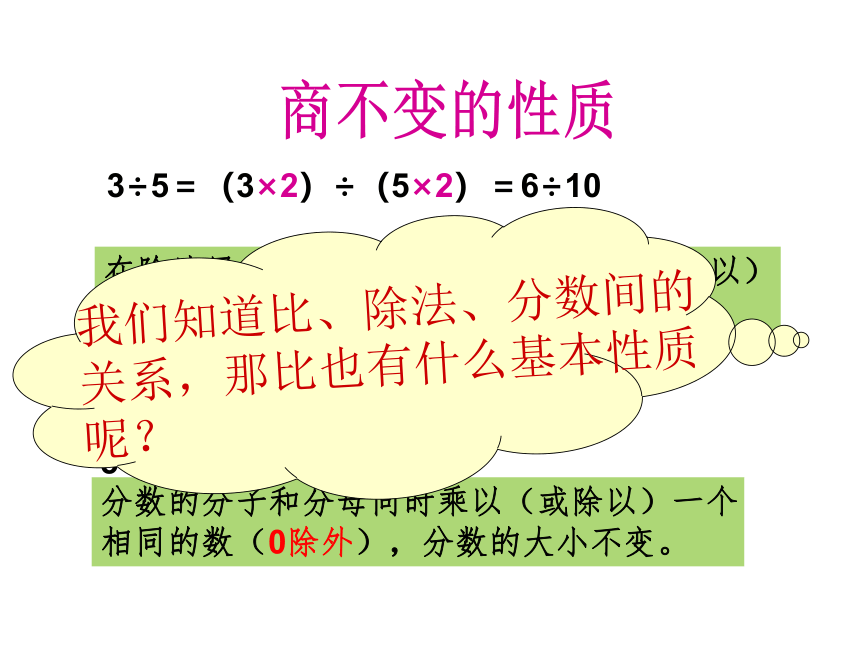
3÷5=(3×2)÷(5×2)=6÷10
5
3
3×2
5×2
10
6
=
=
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
我们知道比、除法、分数间的关系,那比也有什么基本性质呢?
求出下面每个比的比值,
并把比值相等的比填入等式。
5:6 20:24 50:60 60:50
( ):( )=( ):( )
=( ):( )
60
50
24
20
5
6
二、探究新知
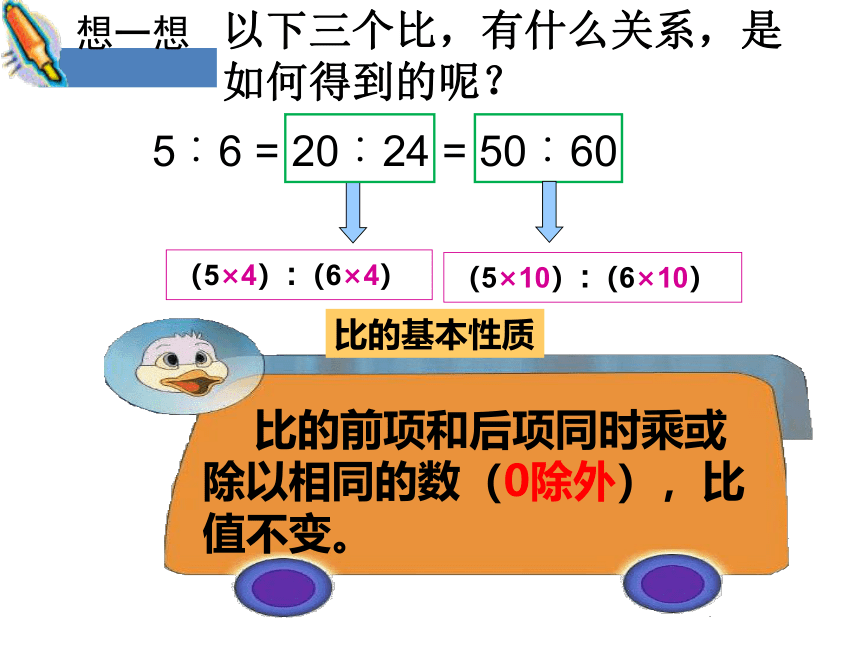
(5×4):(6×4)
5︰6 = 20︰24 = 50︰60
(5×10):(6×10)
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
想一想
以下三个比,有什么关系,是如何得到的呢?
如何把16:20化成4:5
9:12化成3:4
练一练
9︰12
=
3︰4
前项、后项同时除以3
3
4
前、后项必须是整数,而且互质。
应用比的基本性质,可以把复杂比化成 。
最简单的整数比
=(12÷6)∶(18÷6)
= 2∶3
为什么要同时除以6?
12∶18
整数比化简——比的前后项都除以前后项的最大公因数→最简比。
(1)化最简单的整数比。
练一练
77∶63
(拓展1)化最简单的整数比。
=
( )
︰
6
1
9
2
×
18
( )
×
18
=
3︰4
为什么同时乘以18
(2)化成最简单的整数比。
:
6
1
9
2
:
6
1
9
2
分数比化简——比的前后项都乘前后项分母的最小公倍数→整数比→最简比。
为什么同时乘以18
(拓展2)化最简单的整数比。
:
3
2
5
4
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3︰8
(3)化成最简单的整数比。
0.75︰2
小数比化简——比的前后项都扩大相同的倍数→整数比→最简比。
为什么同时乘以100
(拓展3)化最简单的整数比。
0.36︰1.2
归纳化简比的方法:
(1) 整数比
(2) 分数比
(3) 小数比
——比的前后项都除以它们的最大公因数→最简比。
——比的前后项都扩大相同的倍数→整数比→最简比。
——比的前后项都乘它们分母的最小公倍数→整数比→最简比。
不管哪种方法,最后的结果应该是一个 ,而不是一个数。
最简的整数比
1、 在括号里填上适当的数。
8∶5 = 32∶( )
0.5
0.3
=
15∶25 = 3 ∶( )
( )
3
20
5
5
三、巩固新知
2、选择正确的答案。
(1) 9︰6的比值是( )
(A)3 ︰ 2 (B) 1— (C) 2 ︰ 3
(2) ——的最简比是( )
(A)300 ︰ 1 (B)300 (C) 1︰ 300
(3) 0.25 ︰1.25的最简比是( )
(A)25 ︰ 125 (B)1︰ 5 (C) 5︰ 1
1
2
9
0.03
B
A
B
(1)1.2:1.5化简比( )
步骤 1.2:1.5
=(1.2÷0.3):(1.5÷0.3)
=4:5
(2)12:4化简比:12:4=3( )
×
√
12:4=(12÷4):(4÷4)=3:1
3、判断
21∶35 ∶ 1.25∶2
5
6
4
9
4、把下面各比化成最简单的整数比。
∶0.25
5. 把下面各比化成最简单的整数比。
2
5
化简的方法不唯一哦!
102
68
你听说过“黄金比”吗?
四、拓展延伸
书本58页“你知道吗”
黄金比的比值约等于 0.618。从古希腊以来,一直有人认为把黄金比应用于造型艺术,可以使作品给人以最美的感觉。因此,黄金比在日常生活中有着广泛的应用。
宽和长的比值接近0.618的长方形,被认为是最美的。
一幅画的主体部分约占画面的0.618,令人赏心悦目。
五、课堂小结
2、比、除法、分数三者关系
3、我们学过哪些基本性质?
13
18
13
18
13÷18 = =( )∶( )
( )
( )
( )
( )
( )
一、复习准备
3÷5=(3×2)÷(5×2)=6÷10
5
3
3×2
5×2
10
6
=
=
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
我们知道比、除法、分数间的关系,那比也有什么基本性质呢?
求出下面每个比的比值,
并把比值相等的比填入等式。
5:6 20:24 50:60 60:50
( ):( )=( ):( )
=( ):( )
60
50
24
20
5
6
二、探究新知
(5×4):(6×4)
5︰6 = 20︰24 = 50︰60
(5×10):(6×10)
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
比的基本性质
想一想
以下三个比,有什么关系,是如何得到的呢?
如何把16:20化成4:5
9:12化成3:4
练一练
9︰12
=
3︰4
前项、后项同时除以3
3
4
前、后项必须是整数,而且互质。
应用比的基本性质,可以把复杂比化成 。
最简单的整数比
=(12÷6)∶(18÷6)
= 2∶3
为什么要同时除以6?
12∶18
整数比化简——比的前后项都除以前后项的最大公因数→最简比。
(1)化最简单的整数比。
练一练
77∶63
(拓展1)化最简单的整数比。
=
( )
︰
6
1
9
2
×
18
( )
×
18
=
3︰4
为什么同时乘以18
(2)化成最简单的整数比。
:
6
1
9
2
:
6
1
9
2
分数比化简——比的前后项都乘前后项分母的最小公倍数→整数比→最简比。
为什么同时乘以18
(拓展2)化最简单的整数比。
:
3
2
5
4
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3︰8
(3)化成最简单的整数比。
0.75︰2
小数比化简——比的前后项都扩大相同的倍数→整数比→最简比。
为什么同时乘以100
(拓展3)化最简单的整数比。
0.36︰1.2
归纳化简比的方法:
(1) 整数比
(2) 分数比
(3) 小数比
——比的前后项都除以它们的最大公因数→最简比。
——比的前后项都扩大相同的倍数→整数比→最简比。
——比的前后项都乘它们分母的最小公倍数→整数比→最简比。
不管哪种方法,最后的结果应该是一个 ,而不是一个数。
最简的整数比
1、 在括号里填上适当的数。
8∶5 = 32∶( )
0.5
0.3
=
15∶25 = 3 ∶( )
( )
3
20
5
5
三、巩固新知
2、选择正确的答案。
(1) 9︰6的比值是( )
(A)3 ︰ 2 (B) 1— (C) 2 ︰ 3
(2) ——的最简比是( )
(A)300 ︰ 1 (B)300 (C) 1︰ 300
(3) 0.25 ︰1.25的最简比是( )
(A)25 ︰ 125 (B)1︰ 5 (C) 5︰ 1
1
2
9
0.03
B
A
B
(1)1.2:1.5化简比( )
步骤 1.2:1.5
=(1.2÷0.3):(1.5÷0.3)
=4:5
(2)12:4化简比:12:4=3( )
×
√
12:4=(12÷4):(4÷4)=3:1
3、判断
21∶35 ∶ 1.25∶2
5
6
4
9
4、把下面各比化成最简单的整数比。
∶0.25
5. 把下面各比化成最简单的整数比。
2
5
化简的方法不唯一哦!
102
68
你听说过“黄金比”吗?
四、拓展延伸
书本58页“你知道吗”
黄金比的比值约等于 0.618。从古希腊以来,一直有人认为把黄金比应用于造型艺术,可以使作品给人以最美的感觉。因此,黄金比在日常生活中有着广泛的应用。
宽和长的比值接近0.618的长方形,被认为是最美的。
一幅画的主体部分约占画面的0.618,令人赏心悦目。
五、课堂小结
