相似三角形的性质(第一课时)
图片预览

文档简介
课 题 相似三角形的性质(第一课时)
教学目标 1.理解相似三角形中对应线段(对应高、对应中线、对应角平分线)的比都等于相似比的性质;2.能用相似三角形中对应线段的比都等于相似比的性质解决简单的问题;3.经历相似三角形中对应线段的比都等于相似比的性质的探究过程,培养科学全面的分析问题的习惯和简洁准确的语言表达能力.
教材分析 内容分析 教材在安排学习了相似三角形的判定的基础上,进一步研究相似三角形的性质,共三课时,此为第一课时。此课时是本节的重点,也是本章的重点内容之一。是证明线段成比例以及利用相似三角形计算线段长的重要工具,也是研究相似多边形的基础。
教学重点 相似三角形的对应线段之比等于它们的相似比的性质
教学难点 运用相似三角形的对应线段之比等于他们的相似比的性质解决简单的问题
教学方法 自主探索和启发诱导相结合
教学过程
教学环节 教师活动 学生活动 设计意图
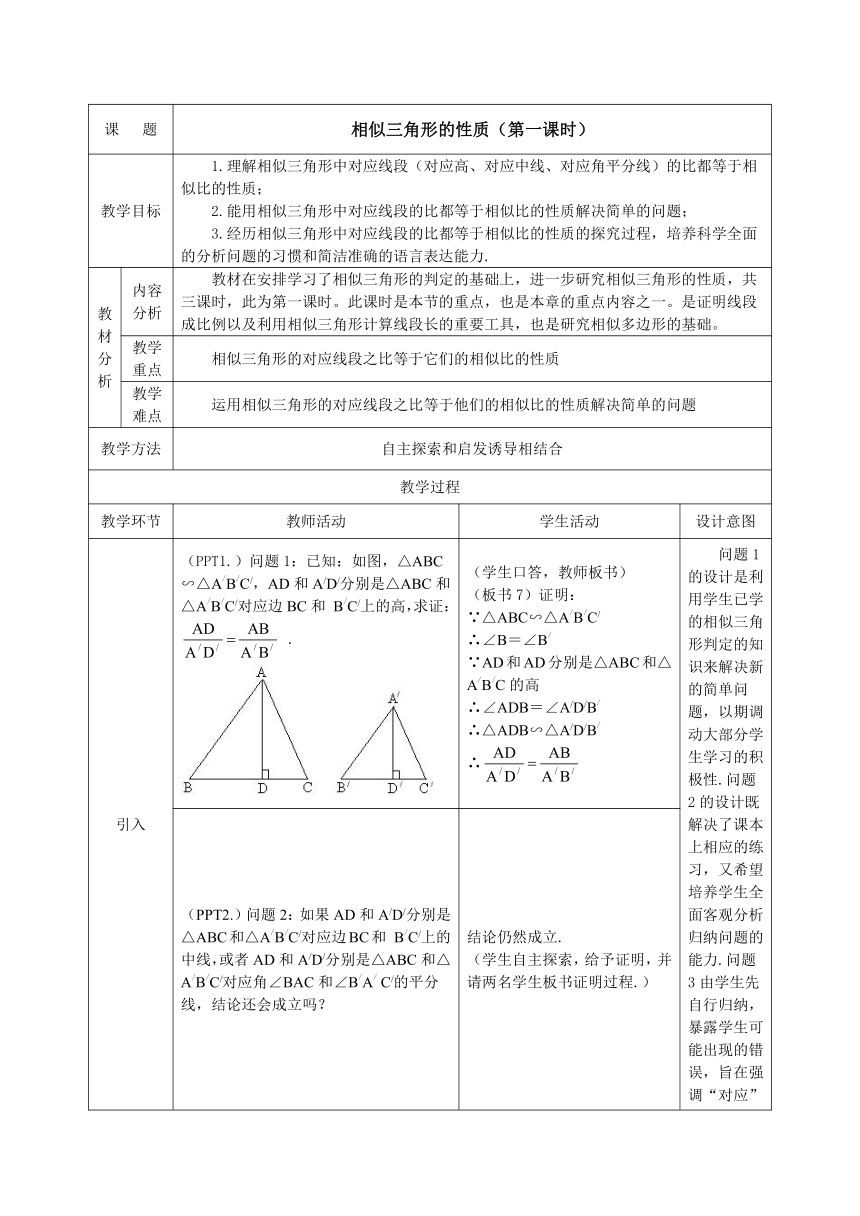
引入 (PPT1.)问题1:已知:如图,△ABC∽△A/B/C/,AD和A/D/分别是△ABC和△A/B/C/对应边BC和 B/C/上的高,求证: . (学生口答,教师板书)(板书7)证明:∵△ABC∽△A/B/C/∴∠B=∠B/∵AD和AD分别是△ABC和△A/B/C的高∴∠ADB=∠A/D/B/∴△ADB∽△A/D/B/∴ 问题1的设计是利用学生已学的相似三角形判定的知识来解决新的简单问题,以期调动大部分学生学习的积极性.问题2的设计既解决了课本上相应的练习,又希望培养学生全面客观分析归纳问题的能力.问题3由学生先自行归纳,暴露学生可能出现的错误,旨在强调“对应”之关系.
(PPT2.)问题2:如果AD和A/D/分别是△ABC和△A/B/C/对应边BC和 B/C/上的中线,或者AD和A/D/分别是△ABC和△A/B/C/对应角∠BAC和∠B/A/ C/的平分线,结论还会成立吗? 结论仍然成立.(学生自主探索,给予证明,并请两名学生板书证明过程.)
问题3:你能用文字语言概述上述问题吗?(先由学生自行归纳) 生A:相似三角形的高之比等于边之比.生B:相似三角形的高之比等于对应边之比.生C:相似三角形的对应高之比等于对应边之比.…… ……
教学环节 教师活动 学生活动 设计意图
新课讲解 提炼概括性质 提问:三位同学谁的说法最准确? 生C. 师生共同用简练的语言概括性质,体现数学性质的简洁美,同时也让学生的认识得到统一.
提问:相似三角形的对应边之比也叫什么? 相似比.
归纳并板书课题(板书1)、性质定理1(板书2):相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比.
性质符号语言及性质外延 (PPT3.)提问:如果△ABC∽△A/B/C/,设相似比等于k,AD、AE、AF分别是△ABC的高、中线、角平分线,A/D/、A/E/、A/F/分别是△A/B/C/的高、中线、角平分线,你能用符号表示相似三角形的性质吗? (板书3)k;k;k. 让学生对“相似三角形的对应线段之比等于它们的相似比的性质”获得深层次的认识.
(PPT4.)判断:如图,△ABC∽△A/B/C/, AD、BE、CF分别是△ABC的高、中线、角平分线,A/D/、B/E/、C/F/分别是△A/B/C/的高、中线、角平分线,下列判断结论是否正确?①,②,③.从中你能得到什么结论? ①、②正确,③错误.(板书4)对应线段的比都相等.
例题讲解 (板书5)例:如图,梯形ABCD中,AD∥BC,∠BAD=90°, AC和BD相交于O,AD=11,BC=21,AB=16,求:点O到AD和点O到BC的距离.思路分析:①结合图形,欲求的点O到AD和点O到BC的距离的另一层涵义是什么?它们与AB有何关系?②图中△AOD和△COB有何关系? ①点O到AD和点O到BC的距离的另一层涵义是分别是△AOD和△COB的高,之和等于AB的长;②△AOD∽△COB;③相似三角形的对应高之比等于对应边之比.(板书6)解:设△AOD和△COB中AD与BC边上的高分别是h1、h2,则h1+h2=AB=16.∵AD∥BC∴∠OAD=∠OCB, 设计一道较简单的例题,考虑大部分学生的学习能力,目的是让班级绝大部分学生都易于接受,同时也能为学生课外独立完成习题第7题做一
教学环节 教师活动 学生活动 设计意图
新课讲解 例题讲解 ③解决这一问题需要用到什么知识?(板书例题及解题过程) ∠ODA=∠OBC∴△AOD∽△COB∴解得:h1=5.5,h2=10.5.答:点O分别到AD、BC的距离分别是5.5,10.5. 点铺垫.
课堂练习 (PPT5.)(课本第80页练习1)已知:△ABC∽△A/B/C/,BC=3.6cm,B/C/=6cm,AE是ABC的一条中线,AE=2.4cm.求△A/B/C/中对应中线A/E/的长.变式1:若AE是△ABC的一条角平分线,AE=3cm,求△A/B/C/中对应角平分线的长.变式2:若AE是△ABC的一条高线,AE=2cm,求△A/B/C/中对应高线的长. (学生板演)练习1:由相似三角形的性质得: 即解得:A/E/=4cm.变式1:对应角平分线的长为5cm.变式2:△A/B/C/中对应高线的长为cm. 运用简单的练习,一方面是为巩固性质,两一方面培养学生严谨规范的解题习惯.通过变式训练进一步熟悉性质.
课堂小结 1.引导学生回顾本节课的主要内容,强调学生理解和运用相似三角形的对应线段之比等于它们的相似比的性质时必须注意“对应”这一基本条件.2.强调学生在学习过程中探究问题时应客观全面地分析问题,注意举一反三、触类旁通. 帮助学生再次领会本节课的重点内容以及分析归纳问题的方法.
课时作业 习题23.3第81页第2、3、7题.
教学设计说明 以往的教学经验表明,学生在理解相似三角形中对应线段(对应高、对应中线、对应角平分线)的比都等于相似比的性质时,往往对“对应”这一条件理解的比较模糊,运用时把握的不够准确.如何让学生理解的更清晰些、把握的更准确些,本节课设计就做了这样的尝试,先让学生自行证明性质,再让学生用文字自行归纳性质,从错误中再认识,反复讨论,甚至激烈争辩,给学生足够的时间让学生发现问题、解决问题,并最终形成共识.本节课的教学设计本着几何教学“小步走”的原则和简单实用的思想,希望班级绝大部分学生能够从课堂45分钟获得最大的收益,教学设计针对的教学对象是普通的初中学生。故设计过程中改变了教参中建议的运用类比的思想方法——即和全等三角形中一些类似的性质类比引出课题,但因为作为普通的九年级学生而言,他们很难回忆出像“全等三角形对应边的高相等”等之类的性质,这里采用了“开门见山”的研究方式,利用学生刚学习的相似三角形的判定的相关知识来探究本节课的话题,我认为应更符合大多数普通学生的认知习惯.
附:板书设计
(板书1)课题:………(板书2)性质定理:……………………………………………………(板书3)数学符号语言:…………………………………………(板书4)说明: ………………………………………… (板书5)例题:……… ………………………………………………………………………………………………………… (板书6)解:……………………………………………………………………………………………………………… (板书7)证明:…… ………………………… ……………………… ……………………… ………………………
学生板演区:
教学目标 1.理解相似三角形中对应线段(对应高、对应中线、对应角平分线)的比都等于相似比的性质;2.能用相似三角形中对应线段的比都等于相似比的性质解决简单的问题;3.经历相似三角形中对应线段的比都等于相似比的性质的探究过程,培养科学全面的分析问题的习惯和简洁准确的语言表达能力.
教材分析 内容分析 教材在安排学习了相似三角形的判定的基础上,进一步研究相似三角形的性质,共三课时,此为第一课时。此课时是本节的重点,也是本章的重点内容之一。是证明线段成比例以及利用相似三角形计算线段长的重要工具,也是研究相似多边形的基础。
教学重点 相似三角形的对应线段之比等于它们的相似比的性质
教学难点 运用相似三角形的对应线段之比等于他们的相似比的性质解决简单的问题
教学方法 自主探索和启发诱导相结合
教学过程
教学环节 教师活动 学生活动 设计意图
引入 (PPT1.)问题1:已知:如图,△ABC∽△A/B/C/,AD和A/D/分别是△ABC和△A/B/C/对应边BC和 B/C/上的高,求证: . (学生口答,教师板书)(板书7)证明:∵△ABC∽△A/B/C/∴∠B=∠B/∵AD和AD分别是△ABC和△A/B/C的高∴∠ADB=∠A/D/B/∴△ADB∽△A/D/B/∴ 问题1的设计是利用学生已学的相似三角形判定的知识来解决新的简单问题,以期调动大部分学生学习的积极性.问题2的设计既解决了课本上相应的练习,又希望培养学生全面客观分析归纳问题的能力.问题3由学生先自行归纳,暴露学生可能出现的错误,旨在强调“对应”之关系.
(PPT2.)问题2:如果AD和A/D/分别是△ABC和△A/B/C/对应边BC和 B/C/上的中线,或者AD和A/D/分别是△ABC和△A/B/C/对应角∠BAC和∠B/A/ C/的平分线,结论还会成立吗? 结论仍然成立.(学生自主探索,给予证明,并请两名学生板书证明过程.)
问题3:你能用文字语言概述上述问题吗?(先由学生自行归纳) 生A:相似三角形的高之比等于边之比.生B:相似三角形的高之比等于对应边之比.生C:相似三角形的对应高之比等于对应边之比.…… ……
教学环节 教师活动 学生活动 设计意图
新课讲解 提炼概括性质 提问:三位同学谁的说法最准确? 生C. 师生共同用简练的语言概括性质,体现数学性质的简洁美,同时也让学生的认识得到统一.
提问:相似三角形的对应边之比也叫什么? 相似比.
归纳并板书课题(板书1)、性质定理1(板书2):相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比.
性质符号语言及性质外延 (PPT3.)提问:如果△ABC∽△A/B/C/,设相似比等于k,AD、AE、AF分别是△ABC的高、中线、角平分线,A/D/、A/E/、A/F/分别是△A/B/C/的高、中线、角平分线,你能用符号表示相似三角形的性质吗? (板书3)k;k;k. 让学生对“相似三角形的对应线段之比等于它们的相似比的性质”获得深层次的认识.
(PPT4.)判断:如图,△ABC∽△A/B/C/, AD、BE、CF分别是△ABC的高、中线、角平分线,A/D/、B/E/、C/F/分别是△A/B/C/的高、中线、角平分线,下列判断结论是否正确?①,②,③.从中你能得到什么结论? ①、②正确,③错误.(板书4)对应线段的比都相等.
例题讲解 (板书5)例:如图,梯形ABCD中,AD∥BC,∠BAD=90°, AC和BD相交于O,AD=11,BC=21,AB=16,求:点O到AD和点O到BC的距离.思路分析:①结合图形,欲求的点O到AD和点O到BC的距离的另一层涵义是什么?它们与AB有何关系?②图中△AOD和△COB有何关系? ①点O到AD和点O到BC的距离的另一层涵义是分别是△AOD和△COB的高,之和等于AB的长;②△AOD∽△COB;③相似三角形的对应高之比等于对应边之比.(板书6)解:设△AOD和△COB中AD与BC边上的高分别是h1、h2,则h1+h2=AB=16.∵AD∥BC∴∠OAD=∠OCB, 设计一道较简单的例题,考虑大部分学生的学习能力,目的是让班级绝大部分学生都易于接受,同时也能为学生课外独立完成习题第7题做一
教学环节 教师活动 学生活动 设计意图
新课讲解 例题讲解 ③解决这一问题需要用到什么知识?(板书例题及解题过程) ∠ODA=∠OBC∴△AOD∽△COB∴解得:h1=5.5,h2=10.5.答:点O分别到AD、BC的距离分别是5.5,10.5. 点铺垫.
课堂练习 (PPT5.)(课本第80页练习1)已知:△ABC∽△A/B/C/,BC=3.6cm,B/C/=6cm,AE是ABC的一条中线,AE=2.4cm.求△A/B/C/中对应中线A/E/的长.变式1:若AE是△ABC的一条角平分线,AE=3cm,求△A/B/C/中对应角平分线的长.变式2:若AE是△ABC的一条高线,AE=2cm,求△A/B/C/中对应高线的长. (学生板演)练习1:由相似三角形的性质得: 即解得:A/E/=4cm.变式1:对应角平分线的长为5cm.变式2:△A/B/C/中对应高线的长为cm. 运用简单的练习,一方面是为巩固性质,两一方面培养学生严谨规范的解题习惯.通过变式训练进一步熟悉性质.
课堂小结 1.引导学生回顾本节课的主要内容,强调学生理解和运用相似三角形的对应线段之比等于它们的相似比的性质时必须注意“对应”这一基本条件.2.强调学生在学习过程中探究问题时应客观全面地分析问题,注意举一反三、触类旁通. 帮助学生再次领会本节课的重点内容以及分析归纳问题的方法.
课时作业 习题23.3第81页第2、3、7题.
教学设计说明 以往的教学经验表明,学生在理解相似三角形中对应线段(对应高、对应中线、对应角平分线)的比都等于相似比的性质时,往往对“对应”这一条件理解的比较模糊,运用时把握的不够准确.如何让学生理解的更清晰些、把握的更准确些,本节课设计就做了这样的尝试,先让学生自行证明性质,再让学生用文字自行归纳性质,从错误中再认识,反复讨论,甚至激烈争辩,给学生足够的时间让学生发现问题、解决问题,并最终形成共识.本节课的教学设计本着几何教学“小步走”的原则和简单实用的思想,希望班级绝大部分学生能够从课堂45分钟获得最大的收益,教学设计针对的教学对象是普通的初中学生。故设计过程中改变了教参中建议的运用类比的思想方法——即和全等三角形中一些类似的性质类比引出课题,但因为作为普通的九年级学生而言,他们很难回忆出像“全等三角形对应边的高相等”等之类的性质,这里采用了“开门见山”的研究方式,利用学生刚学习的相似三角形的判定的相关知识来探究本节课的话题,我认为应更符合大多数普通学生的认知习惯.
附:板书设计
(板书1)课题:………(板书2)性质定理:……………………………………………………(板书3)数学符号语言:…………………………………………(板书4)说明: ………………………………………… (板书5)例题:……… ………………………………………………………………………………………………………… (板书6)解:……………………………………………………………………………………………………………… (板书7)证明:…… ………………………… ……………………… ……………………… ………………………
学生板演区:
