25.4圆周角 (第一课时)
图片预览

文档简介
课 题 25.4圆周角 (第一课时)
教学目标 (1)通过本节的学习,理解圆周角的概念,掌握圆周角的性质;(2)准确运用圆周角性质进行简单的计算和证明;(3)由圆周角与圆心角的关系的探索,渗透化归和分类讨论的思想.
教材分析 内容分析 圆周角是圆中又一个基本概念,学习了圆心角与圆周角以后,我们就可以据此研究与圆有关的其他各种角,如顶点在圆外、两边与圆相交的角以及顶点在圆内的角等. 教材通过归纳、类比,总结出在同圆或等圆中圆周角与圆心角之间关系定理,本节课是进一步学习圆周角定理的两个推论的基础;同时也是圆中有关角的计算和圆中有关问题的证明提供必备知识。
教学重点 圆周角的定义和圆周角的性质定理.
教学难点 圆周角定理的证明.
教学方法 启发式和探究式教学法.
教学过程
教学环节 教师活动 学生活动 设计意图
引入 通过对圆中有关知识的学习,我们知道了什么叫圆心角.如图,(1)∠BOC是什么角?这个角有何特点?(2)延长BO交⊙O于A点,连接AC,∠BAC这个角有何特征?(与圆心角概念类比,得到圆周角定义) 问学生回答;( ... )问学生讨论并概括.( ... ) 复习旧知,提出问题,启发学生对圆周角有个初步了解。这种类比教学能让学生更深刻了解圆心角和圆周角的区别,从而加深学生对圆周角概念的了解和掌握.
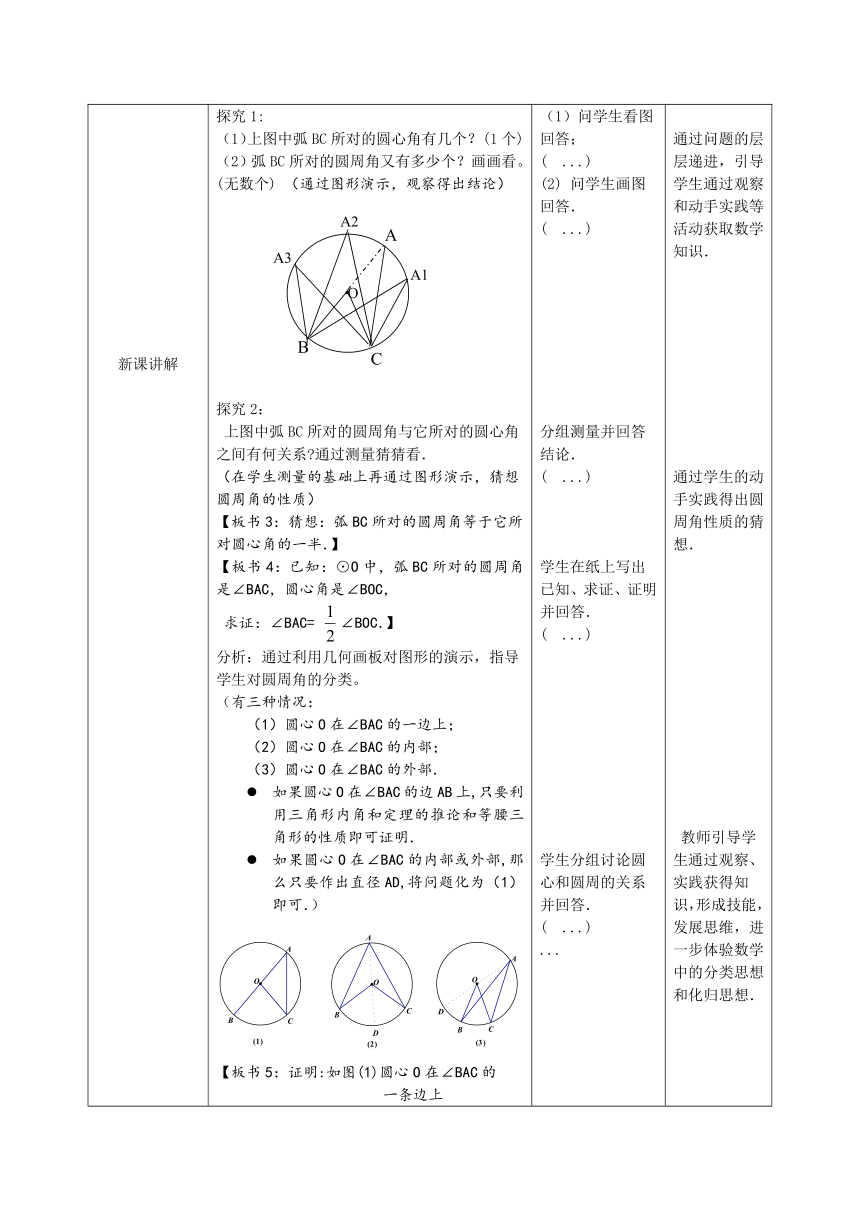
新课讲解新课讲解 【板书1:24.5 圆周角】【板书2:圆周角:顶点在圆上,两边都和圆相交的角.特征:(1)顶点在圆周上;(2)角的两边都和圆相交.】我们今天来学习圆周角和圆周角的性质.探究1:(1)上图中弧BC所对的圆心角有几个?(1个)(2)弧BC所对的圆周角又有多少个?画画看。(无数个) (通过图形演示,观察得出结论)探究2:上图中弧BC所对的圆周角与它所对的圆心角之间有何关系 通过测量猜猜看.(在学生测量的基础上再通过图形演示,猜想圆周角的性质)【板书3:猜想:弧BC所对的圆周角等于它所对圆心角的一半.】 【板书4:已知:⊙O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC, 求证:∠BAC= ∠BOC.】 分析:通过利用几何画板对图形的演示,指导学生对圆周角的分类。(有三种情况:圆心O在∠BAC的一边上; 圆心O在∠BAC的内部;圆心O在∠BAC的外部. 如果圆心O在∠BAC的边AB上,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.如果圆心O在∠BAC的内部或外部,那么只要作出直径AD,将问题化为(1)即可.)【板书5:证明:如图(1)圆心O在∠BAC的一条边上 ∵ OA=OC ∴∠C=∠BAC又∵∠BOC=∠BAC+∠C ∴∠BAC=∠BOC. 如图(2) 圆心O在∠BAC的内部;如图(3) 圆心O在∠BAC的外部.】( 详细证明过程由学生上黑板书写.)【板书6::一条弧所对的圆周角等于它所对圆心角的一半.】(小结:以上证明包含了分类讨论与转化的数学思想,为什么要分类?是因为一段弧所对的圆周角有无限多个,不可能对每个圆周角与圆心角的关系一一证明,此时必须对无限个圆周角进行分类,化无限为有限.) (1)问学生看图回答;( ...)(2) 问学生画图回答.( ...)分组测量并回答结论.( ...)学生在纸上写出已知、求证、证明并回答.( ...)学生分组讨论圆心和圆周的关系并回答.( ...)...学生在纸上书写另外两种情况的证明过程. 总结圆周角的特征,培养学生概括力。为圆周角定义的得出做好准备.通过问题的层层递进,引导学生通过观察和动手实践等活动获取数学知识.通过学生的动手实践得出圆周角性质的猜想.教师引导学生通过观察、实践获得知识,形成技能,发展思维,进一步体验数学中的分类思想和化归思想.锻炼学生的书面表达能力.
例题讲解 【板书7:例1 如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC 】分析: ∠AOB和∠ACB都对着弧AB, ∠BOC和∠BAC都对着弧BC,因此,根据圆周角定理可得出它们之间的关系.【板书8证明:∵∠ACB= ∠AOB ∠BAC= ∠BOC 又∵∠AOB=2∠BOC ∴∠ACB=2∠BAC 】 学生分组讨论并口述证明过程.( ...) 通过例题的讲解,让学生对所学知识巩固和加深.
课堂练习 基础知识训练1.若圆周角等于400,那么它所对的圆心角是 ;若圆心角是1000,则它所对的弧所对的圆周角是 .2.半圆所对的圆周角是 ,直径所对的圆周角是 .3.下列说法正确的是( )A顶点在圆上的角是圆周角 B等弦所对的圆周角相等C等弧所对的圆周角相等 D 90度的角所对的弦是直径4.圆的一条弦等于它的半径,那么这条弦所对的圆周角的度数是( )A 300 B 600 C 1500 D 300或1500 能力提升训练5.已知:如图所示,∠ADC=∠CDB=600,求证:△ABC是等边三角形.( 详细证明过程由学生上黑板书写.) 学生独立思考并回答1、2、3、4。( ...)问题(5)学生分组讨论并书写证明过程. 课堂练习让学生对所学知识进一步加深巩固;同时检测学生对所学知识掌握成度.
课堂小结 1、本节课我们学习了哪些知识?2、本节课的学习中渗透了哪些数学思想?(本节课所学知识:1、圆周角的定义和特征;2、圆周角的性质定理和应用;本节课渗透数学思想:类比,化归,分类等思想.) 培养学生概括能力.
课时作业 教科书29页1、2、3;教科书31页1、2.
板书设计 板书1:24.5 圆周角板书2: 板书4: 板书7: 板书5: 板书8:板书3: 板书6:
教学设计说 明 在学生的最近发展区内进行教学. 如圆周角的概念是在学生已掌握的圆心角基础上进行教学,通过类比圆心角的定义自然引出圆周角的定义.2、重视学习方式的多样化.在探讨、交流、分析中获得数学概念和结论.重视数学知识的形成过程,让学生在自然、合理的过程中领悟知识,感受学习快乐.发现一条弧对着无数个圆周角,不可能逐一证明,怎么办呢?能否把问题分成几种情况?(学生讨论)4、习题设计不仅要注重变式也要多设陷阱.
备 注 本课例讲解的是圆周角教学的第1课时,教材中涉及的例题和推论部分安排在第2课时.
A
C
B
·O
A
C
B
·O
A1
A2
A3
教学目标 (1)通过本节的学习,理解圆周角的概念,掌握圆周角的性质;(2)准确运用圆周角性质进行简单的计算和证明;(3)由圆周角与圆心角的关系的探索,渗透化归和分类讨论的思想.
教材分析 内容分析 圆周角是圆中又一个基本概念,学习了圆心角与圆周角以后,我们就可以据此研究与圆有关的其他各种角,如顶点在圆外、两边与圆相交的角以及顶点在圆内的角等. 教材通过归纳、类比,总结出在同圆或等圆中圆周角与圆心角之间关系定理,本节课是进一步学习圆周角定理的两个推论的基础;同时也是圆中有关角的计算和圆中有关问题的证明提供必备知识。
教学重点 圆周角的定义和圆周角的性质定理.
教学难点 圆周角定理的证明.
教学方法 启发式和探究式教学法.
教学过程
教学环节 教师活动 学生活动 设计意图
引入 通过对圆中有关知识的学习,我们知道了什么叫圆心角.如图,(1)∠BOC是什么角?这个角有何特点?(2)延长BO交⊙O于A点,连接AC,∠BAC这个角有何特征?(与圆心角概念类比,得到圆周角定义) 问学生回答;( ... )问学生讨论并概括.( ... ) 复习旧知,提出问题,启发学生对圆周角有个初步了解。这种类比教学能让学生更深刻了解圆心角和圆周角的区别,从而加深学生对圆周角概念的了解和掌握.
新课讲解新课讲解 【板书1:24.5 圆周角】【板书2:圆周角:顶点在圆上,两边都和圆相交的角.特征:(1)顶点在圆周上;(2)角的两边都和圆相交.】我们今天来学习圆周角和圆周角的性质.探究1:(1)上图中弧BC所对的圆心角有几个?(1个)(2)弧BC所对的圆周角又有多少个?画画看。(无数个) (通过图形演示,观察得出结论)探究2:上图中弧BC所对的圆周角与它所对的圆心角之间有何关系 通过测量猜猜看.(在学生测量的基础上再通过图形演示,猜想圆周角的性质)【板书3:猜想:弧BC所对的圆周角等于它所对圆心角的一半.】 【板书4:已知:⊙O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC, 求证:∠BAC= ∠BOC.】 分析:通过利用几何画板对图形的演示,指导学生对圆周角的分类。(有三种情况:圆心O在∠BAC的一边上; 圆心O在∠BAC的内部;圆心O在∠BAC的外部. 如果圆心O在∠BAC的边AB上,只要利用三角形内角和定理的推论和等腰三角形的性质即可证明.如果圆心O在∠BAC的内部或外部,那么只要作出直径AD,将问题化为(1)即可.)【板书5:证明:如图(1)圆心O在∠BAC的一条边上 ∵ OA=OC ∴∠C=∠BAC又∵∠BOC=∠BAC+∠C ∴∠BAC=∠BOC. 如图(2) 圆心O在∠BAC的内部;如图(3) 圆心O在∠BAC的外部.】( 详细证明过程由学生上黑板书写.)【板书6::一条弧所对的圆周角等于它所对圆心角的一半.】(小结:以上证明包含了分类讨论与转化的数学思想,为什么要分类?是因为一段弧所对的圆周角有无限多个,不可能对每个圆周角与圆心角的关系一一证明,此时必须对无限个圆周角进行分类,化无限为有限.) (1)问学生看图回答;( ...)(2) 问学生画图回答.( ...)分组测量并回答结论.( ...)学生在纸上写出已知、求证、证明并回答.( ...)学生分组讨论圆心和圆周的关系并回答.( ...)...学生在纸上书写另外两种情况的证明过程. 总结圆周角的特征,培养学生概括力。为圆周角定义的得出做好准备.通过问题的层层递进,引导学生通过观察和动手实践等活动获取数学知识.通过学生的动手实践得出圆周角性质的猜想.教师引导学生通过观察、实践获得知识,形成技能,发展思维,进一步体验数学中的分类思想和化归思想.锻炼学生的书面表达能力.
例题讲解 【板书7:例1 如图,OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC 】分析: ∠AOB和∠ACB都对着弧AB, ∠BOC和∠BAC都对着弧BC,因此,根据圆周角定理可得出它们之间的关系.【板书8证明:∵∠ACB= ∠AOB ∠BAC= ∠BOC 又∵∠AOB=2∠BOC ∴∠ACB=2∠BAC 】 学生分组讨论并口述证明过程.( ...) 通过例题的讲解,让学生对所学知识巩固和加深.
课堂练习 基础知识训练1.若圆周角等于400,那么它所对的圆心角是 ;若圆心角是1000,则它所对的弧所对的圆周角是 .2.半圆所对的圆周角是 ,直径所对的圆周角是 .3.下列说法正确的是( )A顶点在圆上的角是圆周角 B等弦所对的圆周角相等C等弧所对的圆周角相等 D 90度的角所对的弦是直径4.圆的一条弦等于它的半径,那么这条弦所对的圆周角的度数是( )A 300 B 600 C 1500 D 300或1500 能力提升训练5.已知:如图所示,∠ADC=∠CDB=600,求证:△ABC是等边三角形.( 详细证明过程由学生上黑板书写.) 学生独立思考并回答1、2、3、4。( ...)问题(5)学生分组讨论并书写证明过程. 课堂练习让学生对所学知识进一步加深巩固;同时检测学生对所学知识掌握成度.
课堂小结 1、本节课我们学习了哪些知识?2、本节课的学习中渗透了哪些数学思想?(本节课所学知识:1、圆周角的定义和特征;2、圆周角的性质定理和应用;本节课渗透数学思想:类比,化归,分类等思想.) 培养学生概括能力.
课时作业 教科书29页1、2、3;教科书31页1、2.
板书设计 板书1:24.5 圆周角板书2: 板书4: 板书7: 板书5: 板书8:板书3: 板书6:
教学设计说 明 在学生的最近发展区内进行教学. 如圆周角的概念是在学生已掌握的圆心角基础上进行教学,通过类比圆心角的定义自然引出圆周角的定义.2、重视学习方式的多样化.在探讨、交流、分析中获得数学概念和结论.重视数学知识的形成过程,让学生在自然、合理的过程中领悟知识,感受学习快乐.发现一条弧对着无数个圆周角,不可能逐一证明,怎么办呢?能否把问题分成几种情况?(学生讨论)4、习题设计不仅要注重变式也要多设陷阱.
备 注 本课例讲解的是圆周角教学的第1课时,教材中涉及的例题和推论部分安排在第2课时.
A
C
B
·O
A
C
B
·O
A1
A2
A3
