3.1体验计算机解决问题的过程 课件(39张幻灯片)
文档属性
| 名称 | 3.1体验计算机解决问题的过程 课件(39张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2020-09-15 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
信息技术基础(必修)
是大家信息素养提升的基础,是学习各选修模块的前提
人工智能初步
算法与程序设计
多媒体技术应用
网络技术应用
数据管理技术
《算法与程序设计》
对你的学习生活有什么帮助?
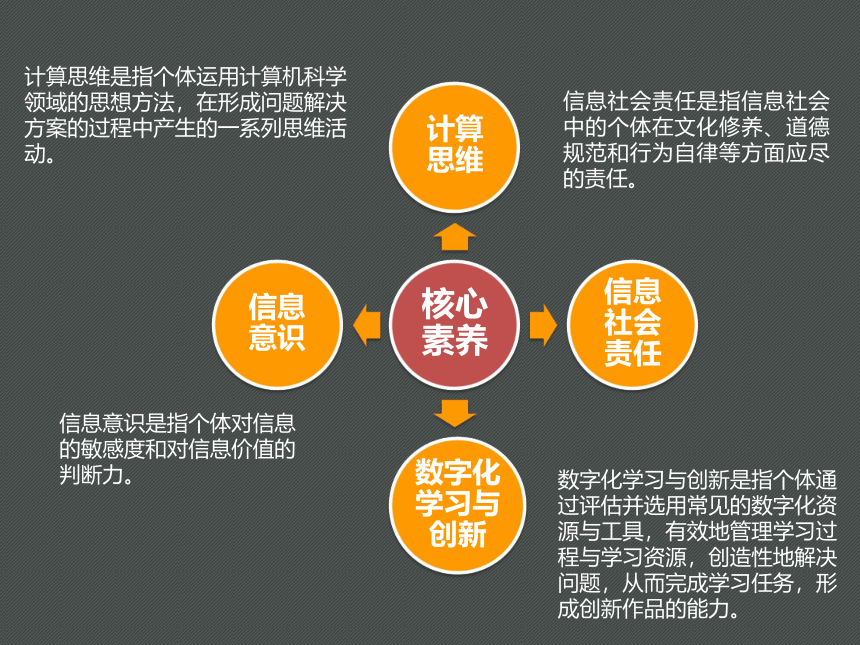
核心素养
计算思维
信息社会责任
数字化学习与创新
信息意识
数字化学习与创新是指个体通过评估并选用常见的数字化资源与工具,有效地管理学习过程与学习资源,创造性地解决问题,从而完成学习任务,形成创新作品的能力。
信息社会责任是指信息社会中的个体在文化修养、道德规范和行为自律等方面应尽的责任。
计算思维是指个体运用计算机科学领域的思想方法,在形成问题解决方案的过程中产生的一系列思维活动。
信息意识是指个体对信息的敏感度和对信息价值的判断力。
编程的重要性已成为越来越多的国际意识的主题,从“极客”的狭隘领域扩展到包括K-12教育领域在内的更广阔的世界。
《算法与程序设计》
包括哪些学习内容?
信息技术必修一第三章
《算法基础》
??
利用计算机和算法高效分析处理数据以解决问题非常重要。
自疫情爆发以来,丁香网第一时间对疫情数据进行分析并做出了信息反馈,成
为大家推荐信任的信息来源,包括了全世界各地的疫情数据统计,疫情地图,
辟谣信息等,科技推动信息透明。
2月1日,浙江省疾控中心上线自动化的全基因组检测分析平台,利用阿里达摩
院研发的AI算法,可将原来数小时的疑似病例基因分析缩短至半小时,大幅缩
短确诊时间,并能精准检测出病毒的变异情况。
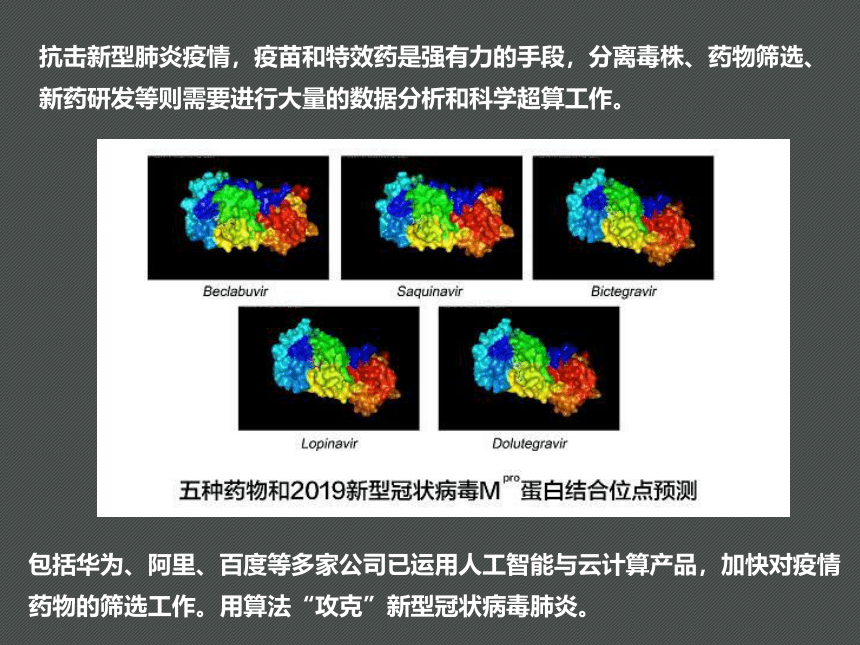
抗击新型肺炎疫情,疫苗和特效药是强有力的手段,分离毒株、药物筛选、
新药研发等则需要进行大量的数据分析和科学超算工作。
包括华为、阿里、百度等多家公司已运用人工智能与云计算产品,加快对疫情
药物的筛选工作。用算法“攻克”新型冠状病毒肺炎。
这堂课,让我们见证了坚强硬核的中国力量!
这堂课,向我们传递了恢宏美好的人性光辉!
这堂课,给我们展示了先进强大的知识力量!
一场疫情,让信息和知识的价值更加显性,让信息更加及时、透明并缓解焦虑;
让技术和大数据等的能力在社会公共事件中更好的发挥作用。
信息技术必修一第四章
《程序设计基础》
??
程学设计语言Python的基础知识
运用顺序结构描述问题求解过程
运用选择结构描述问题求解过程
运用循环结构描述问题求解过程
希望能够成为大家的好老师、好朋友、好伙伴……
课堂上认真思考,敢于提问,积极参与互动!
信息技术必修一第三章
《算法基础》
??
排名第一的中山纪念中学,在近5年来的NOI赛事中屡创佳绩,是全国唯一获一等奖总人次超过200的中学,共229人次获一等奖,其中获得金牌11枚、银牌12枚、铜牌4枚。
2016年计算机编程国际大赛纪中团体总分力压众多世界著名高校,在《THE》发布的“全球学习编程最好的学校排名榜”中,跻身世界第二,是前五名中唯一一所中学;
高嘉煊同学荣获第31届国际信息学奥赛金牌,成为继陈启峰、杨家齐后的广东省第6个国际奖牌获得者;
林凯风、古鸣浩同学分别在18年及19年国际初中生信息学竞赛赛场上夺金。
项目规划与探究
项目主题
项目实施与成果
源于印度的一个古老传说益智类游戏。给定三个柱子,第1个柱子按大小顺序放了若干个圆盘,要求把第一根柱子上的圆盘移到第3个柱子。
移动规则:
(1)每次只能把某个柱子上最上面的盘子移到另一个柱子;
(2)不能出现大盘压小盘的情况。
古代某国王给某被冤枉的大臣64个圆盘,如大臣回答出最少移动次数,国王则对他免于追责。你能帮助这个大臣吗?
汉诺塔游戏
第一节
《体验计算机解决问题的过程》
??
根据需要解决的问题以及给出的条件,采用人工方式解决问题,两人或三人为一小组,运行《汉诺塔1.exe》文件体验游戏,以1、2、3、4个盘子玩游戏,记录下最少移动步数,寻找规律,总结方法。
项目规划与探究
项目主题
项目实施与成果
n=1时,只需要1次移动:
项目规划与探究
项目主题
项目实施与成果
项目规划与探究
项目主题
项目实施与成果
n=2时,需要3次移动:
项目规划与探究
项目主题
项目实施与成果
以此类推,用f(n)表示n个盘子的最少移动次数,可以得到结果如下:
提出问题:
(1)能不能找到f(n)的规律?
(2)如果找到规律的话,怎么利用发现的规律实现《汉诺塔1.exe》“游戏解密”菜单中的“最小步数”功能?
n
1
2
3
4
f(n)
1
3
7
15
项目规划与探究
项目主题
项目实施与成果
项目规划与探究
项目主题
项目实施与成果
方法1:找规律(由小及大、由简入难、由特殊到一般)
如果有足够耐心,可以发现f(5)=31,f(6)=63等等,N再大一些就困难很多。
通过观察,不难发现以下两个规律:
①f(n)=2
f(n-1)+1
②f(n)=2^n-1
n
1
2
3
4
f(n)
1
3
7
15
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
最优策略(找到n个盘子最少移动次数)的核心:要想把n号盘子从1号柱移到3号柱,必须先把上面的n-1个盘子先移到2号柱。
最优策略分三步:
第①步:把n号盘子上面的n-1个盘子从1号柱移到2号柱;
第②步:直接把n号盘子从1号柱移到3号柱;
第③步:把2号柱上的n-1个盘子移到3号柱。
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
增加定义:用g(n,a,b,c)表示把a柱上的n个盘子从a柱经过b柱移到c柱的最少移动步数
则据上有:
g(n,1,2,3)=g(n-1,1,3,2)+1+g(n-1,2,1,3)
探究发现:移动次数跟起始柱、中间柱、目标柱的位置没有关系,只跟盘子数有关系
所以有:g(n,1,2,3)=f(n),
g(n-1,1,3,2)=g(n-1,2,1,3)=f(n-1)
因此f(n)=2
f(n-1)+1成立,验证了规律②。
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
在规律②f(n)=2
f(n-1)+1得到验证的前提下,继续深入研究
上式两边都加1得:f(n)+1=2
(f(n-1)+1)
令g(n)=f(n)+1,则有
g(n)=2
g(n-1)=2^2
g(n-2)=...=2^(n-1)
g(1)
g(1)=f(1)+1=2
g(n)=2^n
f(n)=2^n-1
规律①也获得验证。
项目规划与探究
项目主题
项目实施与成果
我们可以借助计算机,通过编写计算机程序解决问题。编写计算机程序解决问题要经过分析问题、设计算法、编写程序、调试运行程序等若干步骤。
分析问题
设计算法
编写程序
调试运行
检测结果
对于任何一个实际问题,首先要分析该问题的需求情况及已知条件,来判断解决问题的可能性和目标要求,然后对需要解决的问题给出一个精确的描述。在分析问题的过程中,可以采用建立数学模型的方式使问题变得更明确。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
第1步分析问题后得到数学模型,找出解决这个数学模型的方法和步骤,称为设计算法。
前面分析问题得出的两个规律对应的算法描述如下:
规律①f(n)=2^n-1的算法描述:
(1)输入盘子数n;
(2)答案sum=2^n-1;
(3)输出sum,算法结束。
规律②f(n)=2
f(n-1)+1的算法描述:
(1)输入盘子数n;
(2)设置初值f(1)=1;
(3)对于每一个i=2,3,...,n,计算f(i)=2
f(i-1)+1
(4)输出f(n),算法结束。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
根据第2步设计算法后的算法描述,选择一种程序设计语言来编写程序,以实现算法。程序设计语言(如Basic、Pascal、C++、Java、Python等)是人们编程时与计算机沟通的桥梁。一般来说,只要算法确定,语言的选择就没有特别的限定,通常根据问题的特性和编程人员的熟悉程度来选定。
规律①f(n)=2^n-1的算法描述:
(1)输入盘子数n;
(2)答案sum=2^n-1;
(3)输出sum,算法结束。
规律①f(n)=2^n-1的程序代码:
n=int(input())
sum=2
n-1
Print(“最少需要”,sum
,“次”)
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
程序编好以后,通过键盘输入计算机,然后运行程序,看看程序能否按预想的执行。计算机只懂得程序设计语言中所规定的语法规则,如果编写程序时与规则不一致,哪怕是一个标点符号出错,也会令程序出错而中断运行。此时,可以根据计算机提示的出错信息修改程序,重新调试运行。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
程序能够顺利运行以后,还需要对程序功能进行分析和检查,因为如果程序中有逻辑错误,计算机是检查不出来的。
项目规划与探究
项目主题
项目实施与成果
(1)体验运用计算机程序解决问题经历的问题描述、数据抽象和结构分析、模型建立、算法设计、程序编写、程序调试和测试验证等过程;
(2)总结归纳运用计算机解决问题的方法和步骤。
(3)运行《汉诺塔2.exe》文件体验游戏,实现“游戏解密”菜单中的“游戏破解”功能?
信息技术基础(必修)
是大家信息素养提升的基础,是学习各选修模块的前提
人工智能初步
算法与程序设计
多媒体技术应用
网络技术应用
数据管理技术
《算法与程序设计》
对你的学习生活有什么帮助?
核心素养
计算思维
信息社会责任
数字化学习与创新
信息意识
数字化学习与创新是指个体通过评估并选用常见的数字化资源与工具,有效地管理学习过程与学习资源,创造性地解决问题,从而完成学习任务,形成创新作品的能力。
信息社会责任是指信息社会中的个体在文化修养、道德规范和行为自律等方面应尽的责任。
计算思维是指个体运用计算机科学领域的思想方法,在形成问题解决方案的过程中产生的一系列思维活动。
信息意识是指个体对信息的敏感度和对信息价值的判断力。
编程的重要性已成为越来越多的国际意识的主题,从“极客”的狭隘领域扩展到包括K-12教育领域在内的更广阔的世界。
《算法与程序设计》
包括哪些学习内容?
信息技术必修一第三章
《算法基础》
??
利用计算机和算法高效分析处理数据以解决问题非常重要。
自疫情爆发以来,丁香网第一时间对疫情数据进行分析并做出了信息反馈,成
为大家推荐信任的信息来源,包括了全世界各地的疫情数据统计,疫情地图,
辟谣信息等,科技推动信息透明。
2月1日,浙江省疾控中心上线自动化的全基因组检测分析平台,利用阿里达摩
院研发的AI算法,可将原来数小时的疑似病例基因分析缩短至半小时,大幅缩
短确诊时间,并能精准检测出病毒的变异情况。
抗击新型肺炎疫情,疫苗和特效药是强有力的手段,分离毒株、药物筛选、
新药研发等则需要进行大量的数据分析和科学超算工作。
包括华为、阿里、百度等多家公司已运用人工智能与云计算产品,加快对疫情
药物的筛选工作。用算法“攻克”新型冠状病毒肺炎。
这堂课,让我们见证了坚强硬核的中国力量!
这堂课,向我们传递了恢宏美好的人性光辉!
这堂课,给我们展示了先进强大的知识力量!
一场疫情,让信息和知识的价值更加显性,让信息更加及时、透明并缓解焦虑;
让技术和大数据等的能力在社会公共事件中更好的发挥作用。
信息技术必修一第四章
《程序设计基础》
??
程学设计语言Python的基础知识
运用顺序结构描述问题求解过程
运用选择结构描述问题求解过程
运用循环结构描述问题求解过程
希望能够成为大家的好老师、好朋友、好伙伴……
课堂上认真思考,敢于提问,积极参与互动!
信息技术必修一第三章
《算法基础》
??
排名第一的中山纪念中学,在近5年来的NOI赛事中屡创佳绩,是全国唯一获一等奖总人次超过200的中学,共229人次获一等奖,其中获得金牌11枚、银牌12枚、铜牌4枚。
2016年计算机编程国际大赛纪中团体总分力压众多世界著名高校,在《THE》发布的“全球学习编程最好的学校排名榜”中,跻身世界第二,是前五名中唯一一所中学;
高嘉煊同学荣获第31届国际信息学奥赛金牌,成为继陈启峰、杨家齐后的广东省第6个国际奖牌获得者;
林凯风、古鸣浩同学分别在18年及19年国际初中生信息学竞赛赛场上夺金。
项目规划与探究
项目主题
项目实施与成果
源于印度的一个古老传说益智类游戏。给定三个柱子,第1个柱子按大小顺序放了若干个圆盘,要求把第一根柱子上的圆盘移到第3个柱子。
移动规则:
(1)每次只能把某个柱子上最上面的盘子移到另一个柱子;
(2)不能出现大盘压小盘的情况。
古代某国王给某被冤枉的大臣64个圆盘,如大臣回答出最少移动次数,国王则对他免于追责。你能帮助这个大臣吗?
汉诺塔游戏
第一节
《体验计算机解决问题的过程》
??
根据需要解决的问题以及给出的条件,采用人工方式解决问题,两人或三人为一小组,运行《汉诺塔1.exe》文件体验游戏,以1、2、3、4个盘子玩游戏,记录下最少移动步数,寻找规律,总结方法。
项目规划与探究
项目主题
项目实施与成果
n=1时,只需要1次移动:
项目规划与探究
项目主题
项目实施与成果
项目规划与探究
项目主题
项目实施与成果
n=2时,需要3次移动:
项目规划与探究
项目主题
项目实施与成果
以此类推,用f(n)表示n个盘子的最少移动次数,可以得到结果如下:
提出问题:
(1)能不能找到f(n)的规律?
(2)如果找到规律的话,怎么利用发现的规律实现《汉诺塔1.exe》“游戏解密”菜单中的“最小步数”功能?
n
1
2
3
4
f(n)
1
3
7
15
项目规划与探究
项目主题
项目实施与成果
项目规划与探究
项目主题
项目实施与成果
方法1:找规律(由小及大、由简入难、由特殊到一般)
如果有足够耐心,可以发现f(5)=31,f(6)=63等等,N再大一些就困难很多。
通过观察,不难发现以下两个规律:
①f(n)=2
f(n-1)+1
②f(n)=2^n-1
n
1
2
3
4
f(n)
1
3
7
15
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
最优策略(找到n个盘子最少移动次数)的核心:要想把n号盘子从1号柱移到3号柱,必须先把上面的n-1个盘子先移到2号柱。
最优策略分三步:
第①步:把n号盘子上面的n-1个盘子从1号柱移到2号柱;
第②步:直接把n号盘子从1号柱移到3号柱;
第③步:把2号柱上的n-1个盘子移到3号柱。
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
增加定义:用g(n,a,b,c)表示把a柱上的n个盘子从a柱经过b柱移到c柱的最少移动步数
则据上有:
g(n,1,2,3)=g(n-1,1,3,2)+1+g(n-1,2,1,3)
探究发现:移动次数跟起始柱、中间柱、目标柱的位置没有关系,只跟盘子数有关系
所以有:g(n,1,2,3)=f(n),
g(n-1,1,3,2)=g(n-1,2,1,3)=f(n-1)
因此f(n)=2
f(n-1)+1成立,验证了规律②。
项目规划与探究
项目主题
项目实施与成果
方法2:严谨推理
在规律②f(n)=2
f(n-1)+1得到验证的前提下,继续深入研究
上式两边都加1得:f(n)+1=2
(f(n-1)+1)
令g(n)=f(n)+1,则有
g(n)=2
g(n-1)=2^2
g(n-2)=...=2^(n-1)
g(1)
g(1)=f(1)+1=2
g(n)=2^n
f(n)=2^n-1
规律①也获得验证。
项目规划与探究
项目主题
项目实施与成果
我们可以借助计算机,通过编写计算机程序解决问题。编写计算机程序解决问题要经过分析问题、设计算法、编写程序、调试运行程序等若干步骤。
分析问题
设计算法
编写程序
调试运行
检测结果
对于任何一个实际问题,首先要分析该问题的需求情况及已知条件,来判断解决问题的可能性和目标要求,然后对需要解决的问题给出一个精确的描述。在分析问题的过程中,可以采用建立数学模型的方式使问题变得更明确。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
第1步分析问题后得到数学模型,找出解决这个数学模型的方法和步骤,称为设计算法。
前面分析问题得出的两个规律对应的算法描述如下:
规律①f(n)=2^n-1的算法描述:
(1)输入盘子数n;
(2)答案sum=2^n-1;
(3)输出sum,算法结束。
规律②f(n)=2
f(n-1)+1的算法描述:
(1)输入盘子数n;
(2)设置初值f(1)=1;
(3)对于每一个i=2,3,...,n,计算f(i)=2
f(i-1)+1
(4)输出f(n),算法结束。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
根据第2步设计算法后的算法描述,选择一种程序设计语言来编写程序,以实现算法。程序设计语言(如Basic、Pascal、C++、Java、Python等)是人们编程时与计算机沟通的桥梁。一般来说,只要算法确定,语言的选择就没有特别的限定,通常根据问题的特性和编程人员的熟悉程度来选定。
规律①f(n)=2^n-1的算法描述:
(1)输入盘子数n;
(2)答案sum=2^n-1;
(3)输出sum,算法结束。
规律①f(n)=2^n-1的程序代码:
n=int(input())
sum=2
n-1
Print(“最少需要”,sum
,“次”)
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
程序编好以后,通过键盘输入计算机,然后运行程序,看看程序能否按预想的执行。计算机只懂得程序设计语言中所规定的语法规则,如果编写程序时与规则不一致,哪怕是一个标点符号出错,也会令程序出错而中断运行。此时,可以根据计算机提示的出错信息修改程序,重新调试运行。
项目规划与探究
项目主题
项目实施与成果
分析问题
设计算法
编写程序
调试运行
检测结果
程序能够顺利运行以后,还需要对程序功能进行分析和检查,因为如果程序中有逻辑错误,计算机是检查不出来的。
项目规划与探究
项目主题
项目实施与成果
(1)体验运用计算机程序解决问题经历的问题描述、数据抽象和结构分析、模型建立、算法设计、程序编写、程序调试和测试验证等过程;
(2)总结归纳运用计算机解决问题的方法和步骤。
(3)运行《汉诺塔2.exe》文件体验游戏,实现“游戏解密”菜单中的“游戏破解”功能?
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
