人教版数学九年级上册22.3 第3课时 二次函数与拱桥类问题 课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册22.3 第3课时 二次函数与拱桥类问题 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 14:04:05 | ||
图片预览






文档简介
(共18张PPT)
第二十二章 二次函数
22.3 第3课时 二次函数与拱桥类问题
随堂演练
课堂小结
知识回顾
例题讲解
知识回顾
情景导入
22.3 第3课时 二次函数与拱桥类问题
知识回顾
情景导入
我校九年级学生姚小鸣同学怀着激动的心情前往广州观看亚运会开幕式表演.现在先让我们和姚小鸣一起逛逛美丽的广州吧!
22.3 第3课时 二次函数与拱桥类问题
22.3 第3课时 二次函数与拱桥类问题
探究 如图是一座抛物线形拱桥,当拱桥顶离水面 2 m时,水面宽 4 m。水面下降 1 m, 水面宽度为多少?水面宽度增加多少 ?
知识回顾
例题讲解
22.3 第3课时 二次函数与拱桥类问题
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
22.3 第3课时 二次函数与拱桥类问题
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
当水面下降1 m时,水面的纵坐标为-3.请你根据上面的
函数解析式求出这时的水面宽度.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
水面下降1 m,水面宽度增加________m.
22.3 第3课时 二次函数与拱桥类问题
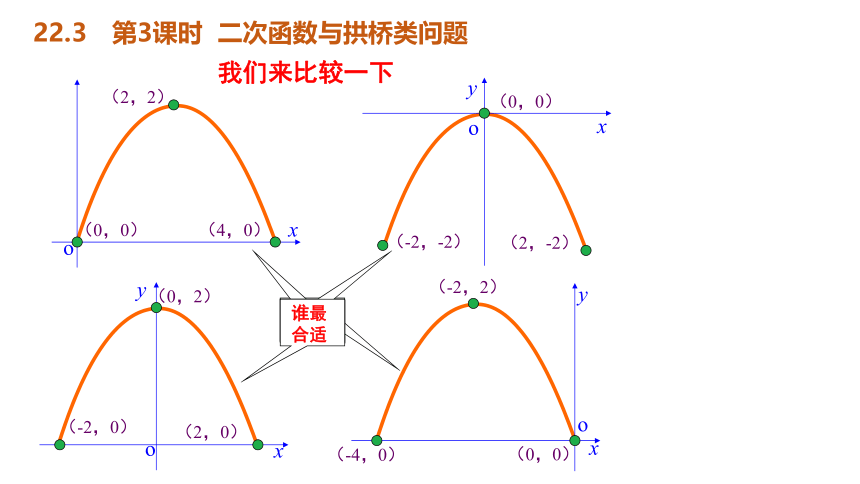
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最
合适
y
y
y
o
o
o
o
x
x
x
x
22.3 第3课时 二次函数与拱桥类问题
解决抛物线型建筑问题“三步骤”:
1.建:根据题意,建立恰当的坐标系,设抛物线解析式;
2.转:准确转化线段的长与点的坐标之间的关系,得到
抛物线上点的坐标,
3.求:代入解析式,求出二次函数解析式;
3.用:应用所求解析式及性质解决问题.
22.3 第3课时 二次函数与拱桥类问题
随堂演练
河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如
图所示的平面直角坐标系,其函数的关系 式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
22.3 第3课时 二次函数与拱桥类问题
2.如图是一个横断面为抛物线形状的拱桥,当水面宽4 m时,拱顶(拱桥洞的最高点)离水面2 m,当水面上升1 m时,水面的宽为( )
A
22.3 第3课时 二次函数与拱桥类问题
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
22.3 第3课时 二次函数与拱桥类问题
4.如图,有一座抛物线形拱桥,桥下面在正常水位AB时宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)建立适当的直角坐标系,求抛物线的函数解析式;
(2)若洪水到来时水位以0.2 m/h的速度上升,从正常水位开始,再过几小时就能到达桥面?
22.3 第3课时 二次函数与拱桥类问题
解:(1)(答案不唯一)建立如图所示的直角坐标系,则点D的横坐标为5,点B的横坐标为10,EF=3 m.
设 OE=h m,则OF=(h-3)m,
则点B(10,-h),D(5,3-h).
设抛物线的函数解析式为y=ax2,
∴抛物线的函数解析式为
(2)∵OE=4 m,∴4÷0.2=20(h).
答:从正常水位开始,再过20 h就能到达桥面.
22.3 第3课时 二次函数与拱桥类问题
5.如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=-5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15 m时,飞行的时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?
22.3 第3课时 二次函数与拱桥类问题
解:(1)当y=15时,有-5x2+20x=15,
解得x1=1,x2=3,
即飞行的时间是1 s或3 s.
(2)令y=0,得-5x2+20x=0,
解得x1=0,x2=4,
所以小球从飞出到落地所用时间是4-0=4(s).
故在飞行过程中,小球在飞行时间为2 s时达到最大高度20 m.
22.3 第3课时 二次函数与拱桥类问题
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用 表示.
x
y
-1
-3
-1
-3
1
3
1
3
O
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
思维拓展
22.3 第3课时 二次函数与拱桥类问题
课堂小结
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
谢 谢 观 看!
第二十二章 二次函数
22.3 第3课时 二次函数与拱桥类问题
随堂演练
课堂小结
知识回顾
例题讲解
知识回顾
情景导入
22.3 第3课时 二次函数与拱桥类问题
知识回顾
情景导入
我校九年级学生姚小鸣同学怀着激动的心情前往广州观看亚运会开幕式表演.现在先让我们和姚小鸣一起逛逛美丽的广州吧!
22.3 第3课时 二次函数与拱桥类问题
22.3 第3课时 二次函数与拱桥类问题
探究 如图是一座抛物线形拱桥,当拱桥顶离水面 2 m时,水面宽 4 m。水面下降 1 m, 水面宽度为多少?水面宽度增加多少 ?
知识回顾
例题讲解
22.3 第3课时 二次函数与拱桥类问题
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
22.3 第3课时 二次函数与拱桥类问题
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-
这条抛物线表示的二次函数为y=- x2.
当水面下降1 m时,水面的纵坐标为-3.请你根据上面的
函数解析式求出这时的水面宽度.
当y=-3时,- x2=-3,解得x1= ,x2=- (舍去).
所以当水面下降1 m时,水面宽度为 m.
水面下降1 m,水面宽度增加________m.
22.3 第3课时 二次函数与拱桥类问题
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最
合适
y
y
y
o
o
o
o
x
x
x
x
22.3 第3课时 二次函数与拱桥类问题
解决抛物线型建筑问题“三步骤”:
1.建:根据题意,建立恰当的坐标系,设抛物线解析式;
2.转:准确转化线段的长与点的坐标之间的关系,得到
抛物线上点的坐标,
3.求:代入解析式,求出二次函数解析式;
3.用:应用所求解析式及性质解决问题.
22.3 第3课时 二次函数与拱桥类问题
随堂演练
河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如
图所示的平面直角坐标系,其函数的关系 式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB 为( )
A.-20 m B.10 m
C.20 m D.-10 m
C
22.3 第3课时 二次函数与拱桥类问题
2.如图是一个横断面为抛物线形状的拱桥,当水面宽4 m时,拱顶(拱桥洞的最高点)离水面2 m,当水面上升1 m时,水面的宽为( )
A
22.3 第3课时 二次函数与拱桥类问题
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
4
22.3 第3课时 二次函数与拱桥类问题
4.如图,有一座抛物线形拱桥,桥下面在正常水位AB时宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)建立适当的直角坐标系,求抛物线的函数解析式;
(2)若洪水到来时水位以0.2 m/h的速度上升,从正常水位开始,再过几小时就能到达桥面?
22.3 第3课时 二次函数与拱桥类问题
解:(1)(答案不唯一)建立如图所示的直角坐标系,则点D的横坐标为5,点B的横坐标为10,EF=3 m.
设 OE=h m,则OF=(h-3)m,
则点B(10,-h),D(5,3-h).
设抛物线的函数解析式为y=ax2,
∴抛物线的函数解析式为
(2)∵OE=4 m,∴4÷0.2=20(h).
答:从正常水位开始,再过20 h就能到达桥面.
22.3 第3课时 二次函数与拱桥类问题
5.如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=-5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15 m时,飞行的时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?
22.3 第3课时 二次函数与拱桥类问题
解:(1)当y=15时,有-5x2+20x=15,
解得x1=1,x2=3,
即飞行的时间是1 s或3 s.
(2)令y=0,得-5x2+20x=0,
解得x1=0,x2=4,
所以小球从飞出到落地所用时间是4-0=4(s).
故在飞行过程中,小球在飞行时间为2 s时达到最大高度20 m.
22.3 第3课时 二次函数与拱桥类问题
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用 表示.
x
y
-1
-3
-1
-3
1
3
1
3
O
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗?
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
思维拓展
22.3 第3课时 二次函数与拱桥类问题
课堂小结
拱桥问题
运动中的抛物线问题
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
转化的关键
谢 谢 观 看!
同课章节目录
