人教版数学九年级上册:22.3 实际问题与二次函数 教案( 第1课时 表格式)
文档属性
| 名称 | 人教版数学九年级上册:22.3 实际问题与二次函数 教案( 第1课时 表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 17:53:32 | ||
图片预览


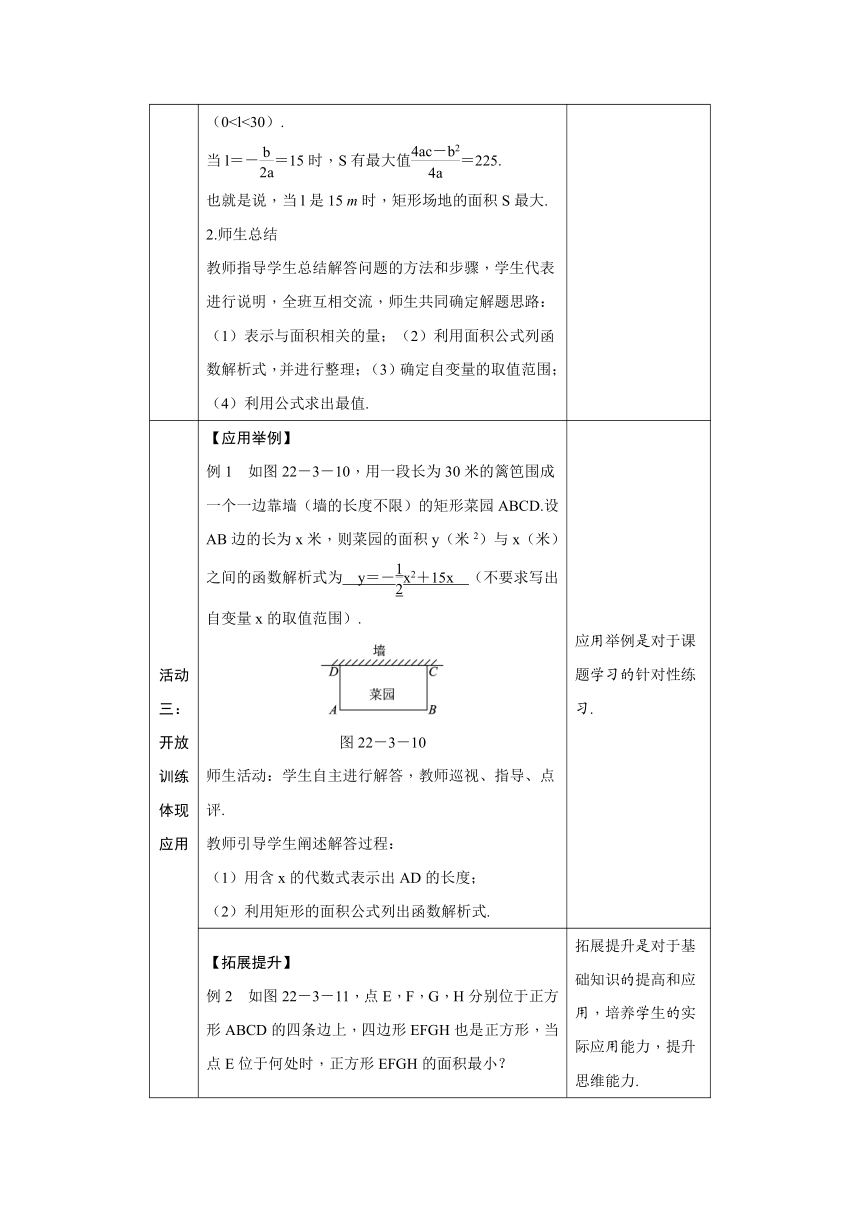

文档简介
22.3 实际问题与二次函数
第1课时 二次函数与图形面积问题
课题
第1课时 二次函数与图形面积问题
授课人
教
学
目
标
知识技能
1.通过图形的面积关系列出函数解析式;
2.用二次函数的知识分析解决有关面积的实际问题.
数学思考
对实际问题的探究,体会数学知识的现实意义,进一步认识利用二次函数的有关知识解决实际问题.
问题解决
通过实际问题与二次函数的关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)的方法.
情感态度
体会数学是解决实际问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用.
教学重点
用二次函数的知识分析解决有关面积的实际问题.
教学难点
通过图形的面积关系列出函数解析式.
授课类型
新授课
课时
教具
多媒体
教学活动
教学步骤
师生活动
设计意图
回顾
1.请写出下列抛物线的开口方向、对称轴和顶点坐标:
(1)y=6x2+12x;(2)y=-4x2+8x-10.
2.以上两个函数,哪个函数有最大值,哪个函数有最小值?并说出两个函数的最大值或最小值分别是多少.
师生活动:学生自主进行解答,教师做好指导和点评.
提示:求解二次函数的最值一般有两种方法:
一是把一般式化为顶点式;二是利用顶点坐标公式求解.
(1)y=6(x+1)2-6,所以抛物线开口向上,对称轴为直线x=-1,顶点坐标为(-1,-6),当x=-1时,y有最小值-6.
(2)y=-4(x-1)2-6,所以抛物线开口向下,对称轴为直线x=1,顶点坐标为(1,-6),当x=1时,y有最大值-6.
通过回顾二次函数的最值问题,为讲解新课做铺垫,两种求解方法为学生深刻理解知识提供理论支持.
活动
一:
创设
情境
导入
新课
【课堂引入】
问题:用总长为60 m的篱笆围成矩形场地,矩形场地的面积S随一边长l的变化而变化,当l是多少米时,矩形场地的面积S最大?
师生活动:
1.教师引导学生分析与矩形面积相关的量;
2.教师设问,如何用含l的代数式表示与其相邻的边的长度;
3.学生自主列函数解析式,并进行整理,讨论问题解答的正确性;
4.针对问题要求进行求解,并回答问题.
教师关注:
1.学生能否根据矩形的面积公式列函数解析式;
2.学生能否根据以前所学知识准确求出函数的最大值.
通过典型的实际问题,激发学生解答的欲望,让学生在合作中学习,共同解答问题,培养学生的探究能力和合作意识.
活动
二:
实践
探究
交流
新知
1.探究新知
活动一:针对[课堂引入]的问题进行探究,教师总结解题过程.
师生活动:
(1)确定解题的步骤:先表示矩形的长和宽,再利用面积公式列解析式,最后求最值.
(2)解答过程:矩形场地的一边长为l m,则另一边长为(30-l)m,
所以矩形场地的面积S=l(30-l)=-l2+30l(0当l=-=15时,S有最大值=225.
也就是说,当l是15 m时,矩形场地的面积S最大.
2.师生总结
教师指导学生总结解答问题的方法和步骤,学生代表进行说明,全班互相交流,师生共同确定解题思路:
(1)表示与面积相关的量;(2)利用面积公式列函数解析式,并进行整理;(3)确定自变量的取值范围;(4)利用公式求出最值.
通过典型问题的设计和解答,让学生体会函数模型在解决实际问题中的作用.
活动
三:
开放
训练
体现
应用
【应用举例】
如图22-3-10,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD.设AB边的长为x米,则菜园的面积y(米2)与x(米)之间的函数解析式为 y=-x2+15x (不要求写出自变量x的取值范围).
图22-3-10
师生活动:学生自主进行解答,教师巡视、指导、点评.
教师引导学生阐述解答过程:
(1)用含x的代数式表示出AD的长度;
(2)利用矩形的面积公式列出函数解析式.
应用举例是对于课题学习的针对性练习.
【拓展提升】
如图22-3-11,点E,F,G,H分别位于正方形ABCD的四条边上,四边形EFGH也是正方形,当点E位于何处时,正方形EFGH的面积最小?
图22-3-11
师生活动:学生小组内讨论、交流,教师参与小组合作,并引导学生理清解题思路.
教师做好总结和展示:
设AE=x,AB=1,正方形EFGH的面积为y.
根据题意,得y=1-2x(1-x).
整理,得y=2x2-2x+1,
所以当x=0.5时,正方形EFGH的面积最小,最小值为0.5,
即当点E在AB的中点处时,正方形EFGH的面积最小.
拓展提升是对于基础知识的提高和应用,培养学生的实际应用能力,提升思维能力.
活动
四:
课堂
总结
反思
【达标测评】
1.给你一根长为8 m的铁丝,用它围成一个矩形方框,当这个矩形的长为 2 m 时,矩形的面积最大.
2.某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40 m的栅栏围成.若设花园的宽为x m,花园的面积为y m2.
(1)求y与x之间的函数解析式,并写出自变量的取值范围;
(2)根据(1)中求得的函数解析式,描述其图象的变化趋势,并结合题意判断,当x取何值时,花园的面积最大,最大面积是多少?
3.如图22-3-12所示,要建一个矩形养鸡场,养鸡场的一边靠墙,计划用50 m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设养鸡场的长为x m.
(1)要使养鸡场的面积最大,养鸡场的长应为多少米?
(2)如果中间有n道篱笆隔墙,要使养鸡场的面积最大,养鸡场的长应为多少米?
图22-3-12
比较(1)(2)的结果,你能得到什么结论?
学生进行当堂检测,完成后,教师进行批阅、点评、讲解.
针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结:
你在本节课中有哪些收获?有哪些进步?还有哪些困惑?请谈一谈.
教师强调:利用面积公式列函数解析式是解答问题的主要方法.
2.布置作业:
教材第52页习题22.3第4,6题.
小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在创设情境和探究新知环节中,利用实际问题激发学生的求知欲,渗透转化思想,把知识回归生活,又从生活中走出来,使学生乐学、好学;通过层层设疑、由易到难,符合学生的认知水平和认知规律,引导学生不断思考、积极探索.
②[讲授效果反思]
教师提醒学生注意:(1)一般地,面积问题中常把面积作为函数,边长作为自变量;(2)确定自变量的取值范围是解答此类问题的注意点;(3)求最值问题可选用公式法或将函数解析式由一般式化为顶点式.
③[师生互动反思]
从课堂发言和检测来看,学生能够积极发言、小组讨论富有实效,能够把知识进行化归,建立函数模型.
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
典案二 导学设计
学习目标:
1.能够分析和表示实际问题中变量之间的关系,并运用二次函数的知识求出实际中面积的最大(小)值,提高解决问题的能力.
2.经历利用二次函数解决实际问题的过程,感受数学的应用价值,增进对数学的理解和学好数学的信心.
学习过程:
(一)情境创设
木工师傅需要一块面积足够大的矩形木料,但是手边只有一块三角形的木料,怎么样才能锯出一块面积最大的矩形木料呢?小明和小玲给出了自己的建议。谁的建议更合理?请你通过本节课的学习给出答案。
35306026035
(小明) (小玲)
(二)自主探究
38836605715在我市开展的创卫活动中,某居民小区要在一块一边靠墙(墙长为15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示)。怎样围才能使矩形花园面积最大?。
(1)若设花园的BC边长为x(m),AB怎么表示?
AB= m
(2)设花园的面积为y(m2)求y与x之间的函数关系式,并写出自变量x?的取值范围。
(3)当x取何值时,花园的面积最大 ?最大面积为多少?
(三)合作交流
1.自主探究问题
2.回顾本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
388366043180(四)运用规律,巩固新知
完成情境创设的问题。
(五)当堂检测
1.如图,等腰梯形ABCD的周长为4cm,下底角为60?,当梯形的腰长为多少时,梯形的面积最大?最大面积是多少?
303085584455
2.如图,点E、F分别是边长为4的正方形ABCD的边BC,CD上的点,CE=1,CF=false,HM⊥AG,HN⊥AD,设HM=x,矩形AMHN的面积为y
(1)求y与x之间的函数关系式
(2)当x为何值时,矩形AMHN的面积最大?最大面积是多少?
360426084455
3.能力提升:如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由点B沿折线BCD向点D移动,EM⊥AB,EN⊥AD,设BM=x,矩形AMEN的面积为y,那么当x是多少的时候,y值最大,是几?
(六)课外自评
必做:1.某建筑物的窗户如图,它的上半部是半圆,下半部是矩形,窗框材料总长是15m,当x等于多少时,窗户透过的光线最多?此时,面积是多少?
3246120-113665
2.在边长为2m的正方形铁板内,沿着一条边恰好截取两块相邻的正方形板料,要使截取的板料面积最小,应该怎样截取?
第1课时 二次函数与图形面积问题
课题
第1课时 二次函数与图形面积问题
授课人
教
学
目
标
知识技能
1.通过图形的面积关系列出函数解析式;
2.用二次函数的知识分析解决有关面积的实际问题.
数学思考
对实际问题的探究,体会数学知识的现实意义,进一步认识利用二次函数的有关知识解决实际问题.
问题解决
通过实际问题与二次函数的关系的探究,让学生掌握利用顶点坐标解决最大值(或最小值)的方法.
情感态度
体会数学是解决实际问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用.
教学重点
用二次函数的知识分析解决有关面积的实际问题.
教学难点
通过图形的面积关系列出函数解析式.
授课类型
新授课
课时
教具
多媒体
教学活动
教学步骤
师生活动
设计意图
回顾
1.请写出下列抛物线的开口方向、对称轴和顶点坐标:
(1)y=6x2+12x;(2)y=-4x2+8x-10.
2.以上两个函数,哪个函数有最大值,哪个函数有最小值?并说出两个函数的最大值或最小值分别是多少.
师生活动:学生自主进行解答,教师做好指导和点评.
提示:求解二次函数的最值一般有两种方法:
一是把一般式化为顶点式;二是利用顶点坐标公式求解.
(1)y=6(x+1)2-6,所以抛物线开口向上,对称轴为直线x=-1,顶点坐标为(-1,-6),当x=-1时,y有最小值-6.
(2)y=-4(x-1)2-6,所以抛物线开口向下,对称轴为直线x=1,顶点坐标为(1,-6),当x=1时,y有最大值-6.
通过回顾二次函数的最值问题,为讲解新课做铺垫,两种求解方法为学生深刻理解知识提供理论支持.
活动
一:
创设
情境
导入
新课
【课堂引入】
问题:用总长为60 m的篱笆围成矩形场地,矩形场地的面积S随一边长l的变化而变化,当l是多少米时,矩形场地的面积S最大?
师生活动:
1.教师引导学生分析与矩形面积相关的量;
2.教师设问,如何用含l的代数式表示与其相邻的边的长度;
3.学生自主列函数解析式,并进行整理,讨论问题解答的正确性;
4.针对问题要求进行求解,并回答问题.
教师关注:
1.学生能否根据矩形的面积公式列函数解析式;
2.学生能否根据以前所学知识准确求出函数的最大值.
通过典型的实际问题,激发学生解答的欲望,让学生在合作中学习,共同解答问题,培养学生的探究能力和合作意识.
活动
二:
实践
探究
交流
新知
1.探究新知
活动一:针对[课堂引入]的问题进行探究,教师总结解题过程.
师生活动:
(1)确定解题的步骤:先表示矩形的长和宽,再利用面积公式列解析式,最后求最值.
(2)解答过程:矩形场地的一边长为l m,则另一边长为(30-l)m,
所以矩形场地的面积S=l(30-l)=-l2+30l(0
也就是说,当l是15 m时,矩形场地的面积S最大.
2.师生总结
教师指导学生总结解答问题的方法和步骤,学生代表进行说明,全班互相交流,师生共同确定解题思路:
(1)表示与面积相关的量;(2)利用面积公式列函数解析式,并进行整理;(3)确定自变量的取值范围;(4)利用公式求出最值.
通过典型问题的设计和解答,让学生体会函数模型在解决实际问题中的作用.
活动
三:
开放
训练
体现
应用
【应用举例】
如图22-3-10,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD.设AB边的长为x米,则菜园的面积y(米2)与x(米)之间的函数解析式为 y=-x2+15x (不要求写出自变量x的取值范围).
图22-3-10
师生活动:学生自主进行解答,教师巡视、指导、点评.
教师引导学生阐述解答过程:
(1)用含x的代数式表示出AD的长度;
(2)利用矩形的面积公式列出函数解析式.
应用举例是对于课题学习的针对性练习.
【拓展提升】
如图22-3-11,点E,F,G,H分别位于正方形ABCD的四条边上,四边形EFGH也是正方形,当点E位于何处时,正方形EFGH的面积最小?
图22-3-11
师生活动:学生小组内讨论、交流,教师参与小组合作,并引导学生理清解题思路.
教师做好总结和展示:
设AE=x,AB=1,正方形EFGH的面积为y.
根据题意,得y=1-2x(1-x).
整理,得y=2x2-2x+1,
所以当x=0.5时,正方形EFGH的面积最小,最小值为0.5,
即当点E在AB的中点处时,正方形EFGH的面积最小.
拓展提升是对于基础知识的提高和应用,培养学生的实际应用能力,提升思维能力.
活动
四:
课堂
总结
反思
【达标测评】
1.给你一根长为8 m的铁丝,用它围成一个矩形方框,当这个矩形的长为 2 m 时,矩形的面积最大.
2.某居民小区要在一块一边靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40 m的栅栏围成.若设花园的宽为x m,花园的面积为y m2.
(1)求y与x之间的函数解析式,并写出自变量的取值范围;
(2)根据(1)中求得的函数解析式,描述其图象的变化趋势,并结合题意判断,当x取何值时,花园的面积最大,最大面积是多少?
3.如图22-3-12所示,要建一个矩形养鸡场,养鸡场的一边靠墙,计划用50 m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设养鸡场的长为x m.
(1)要使养鸡场的面积最大,养鸡场的长应为多少米?
(2)如果中间有n道篱笆隔墙,要使养鸡场的面积最大,养鸡场的长应为多少米?
图22-3-12
比较(1)(2)的结果,你能得到什么结论?
学生进行当堂检测,完成后,教师进行批阅、点评、讲解.
针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结:
你在本节课中有哪些收获?有哪些进步?还有哪些困惑?请谈一谈.
教师强调:利用面积公式列函数解析式是解答问题的主要方法.
2.布置作业:
教材第52页习题22.3第4,6题.
小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在创设情境和探究新知环节中,利用实际问题激发学生的求知欲,渗透转化思想,把知识回归生活,又从生活中走出来,使学生乐学、好学;通过层层设疑、由易到难,符合学生的认知水平和认知规律,引导学生不断思考、积极探索.
②[讲授效果反思]
教师提醒学生注意:(1)一般地,面积问题中常把面积作为函数,边长作为自变量;(2)确定自变量的取值范围是解答此类问题的注意点;(3)求最值问题可选用公式法或将函数解析式由一般式化为顶点式.
③[师生互动反思]
从课堂发言和检测来看,学生能够积极发言、小组讨论富有实效,能够把知识进行化归,建立函数模型.
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
典案二 导学设计
学习目标:
1.能够分析和表示实际问题中变量之间的关系,并运用二次函数的知识求出实际中面积的最大(小)值,提高解决问题的能力.
2.经历利用二次函数解决实际问题的过程,感受数学的应用价值,增进对数学的理解和学好数学的信心.
学习过程:
(一)情境创设
木工师傅需要一块面积足够大的矩形木料,但是手边只有一块三角形的木料,怎么样才能锯出一块面积最大的矩形木料呢?小明和小玲给出了自己的建议。谁的建议更合理?请你通过本节课的学习给出答案。
35306026035
(小明) (小玲)
(二)自主探究
38836605715在我市开展的创卫活动中,某居民小区要在一块一边靠墙(墙长为15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示)。怎样围才能使矩形花园面积最大?。
(1)若设花园的BC边长为x(m),AB怎么表示?
AB= m
(2)设花园的面积为y(m2)求y与x之间的函数关系式,并写出自变量x?的取值范围。
(3)当x取何值时,花园的面积最大 ?最大面积为多少?
(三)合作交流
1.自主探究问题
2.回顾本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
388366043180(四)运用规律,巩固新知
完成情境创设的问题。
(五)当堂检测
1.如图,等腰梯形ABCD的周长为4cm,下底角为60?,当梯形的腰长为多少时,梯形的面积最大?最大面积是多少?
303085584455
2.如图,点E、F分别是边长为4的正方形ABCD的边BC,CD上的点,CE=1,CF=false,HM⊥AG,HN⊥AD,设HM=x,矩形AMHN的面积为y
(1)求y与x之间的函数关系式
(2)当x为何值时,矩形AMHN的面积最大?最大面积是多少?
360426084455
3.能力提升:如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由点B沿折线BCD向点D移动,EM⊥AB,EN⊥AD,设BM=x,矩形AMEN的面积为y,那么当x是多少的时候,y值最大,是几?
(六)课外自评
必做:1.某建筑物的窗户如图,它的上半部是半圆,下半部是矩形,窗框材料总长是15m,当x等于多少时,窗户透过的光线最多?此时,面积是多少?
3246120-113665
2.在边长为2m的正方形铁板内,沿着一条边恰好截取两块相邻的正方形板料,要使截取的板料面积最小,应该怎样截取?
同课章节目录
