人教版数学九年级上册:22.3 实际问题与二次函数 教案( 第3课时 表格式)
文档属性
| 名称 | 人教版数学九年级上册:22.3 实际问题与二次函数 教案( 第3课时 表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 460.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 17:54:58 | ||
图片预览


文档简介
22.3 实际问题与二次函数
第3课时 二次函数与拱桥类问题
课题
第3课时 二次函数与拱桥类问题
授课人
教
学
目
标
知识技能
1.能根据具体的问题情境建立数学模型,应用二次函数的知识求解,并根据具体问题的实际意义检验结果的合理性;
2.学会从多个角度思考问题,逐步提高解决问题的能力.
数学思考
1.通过对实际问题的研究,体会建模的数学思想;
2.经历将实际问题抽象为数学问题的过程,体会转化和数形结合的思想.
问题解决
通过问题的设计、解答,使学生学会从不同角度寻求解决问题的方法,获得解决问题的经验.
情感态度
1.通过小组合作交流,提高合作意识,培养创新精神;
2.通过用二次函数的知识解决实际问题,体会数学与现实生活的紧密联系,提高学习数学的兴趣,增强应用数学的意识.
教学重点
探究应用二次函数的知识解决实际问题的方法.
教学难点
如何从实际问题中抽象出数学问题,建立数学模型.
授课类型
新授课
课时
教具
多媒体
教学活动
教学步骤
师生活动
设计意图
回顾
1.二次函数解析式常见的形式有哪几种?并说明其特征.
2.对二次函数y=ax2+bx+c的图象进行平移时:
向上平移k(k>0)个单位长度得到的图象对应的函数解析式是什么?
向下平移k(k>0)个单位长度得到的图象对应的函数解析式是什么?
向左平移h(h>0)个单位长度得到的图象对应的函数解析式是什么?
向右平移h(h>0)个单位长度得到的图象对应的函数解析式是什么?
师生活动:教师引导学生回忆知识,学生进行解答,教师做好点评.
在已有知识的基础上提出新的问题,能为学生营造一个主动思考、探索的氛围,激发学生的学习兴趣.
活动
一:
创设
情境
导入
新课
【课堂引入】
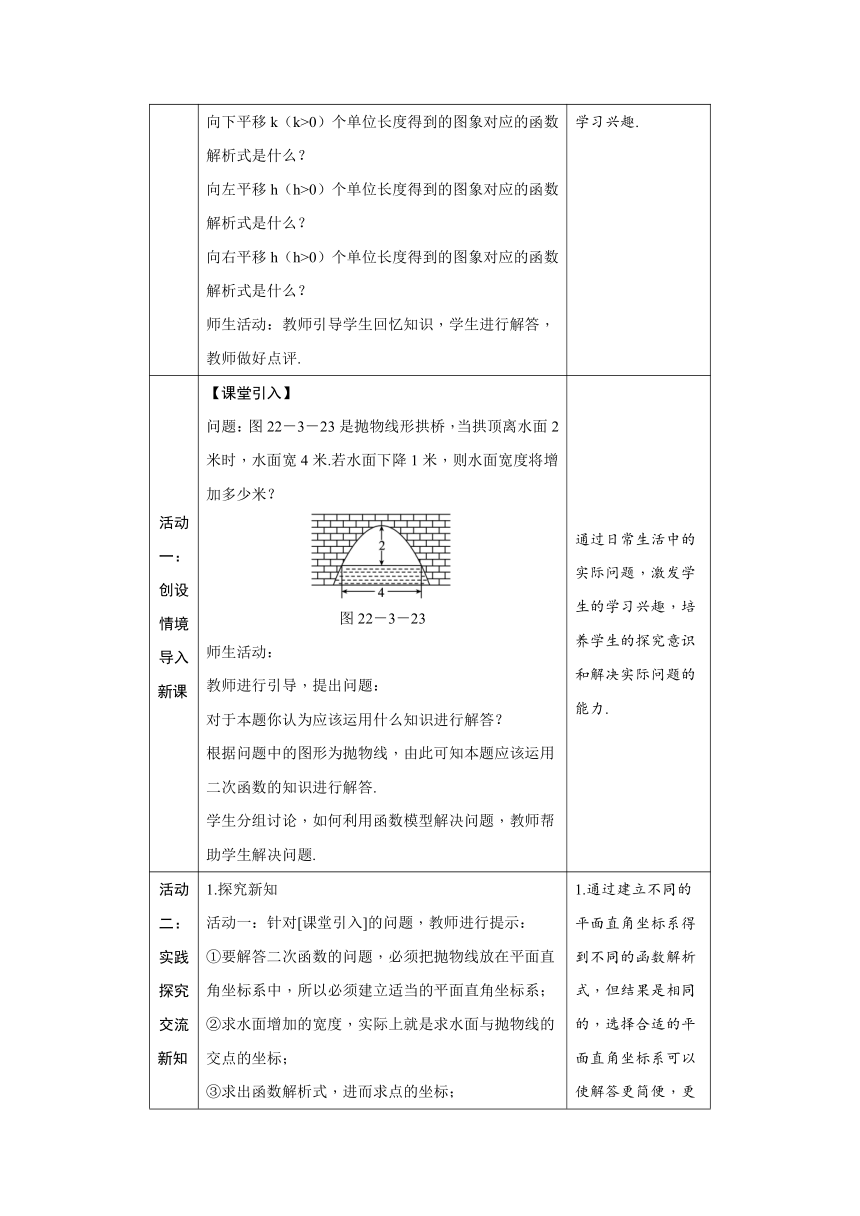
问题:图22-3-23是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米?
图22-3-23
师生活动:
教师进行引导,提出问题:
对于本题你认为应该运用什么知识进行解答?
根据问题中的图形为抛物线,由此可知本题应该运用二次函数的知识进行解答.
学生分组讨论,如何利用函数模型解决问题,教师帮助学生解决问题.
通过日常生活中的实际问题,激发学生的学习兴趣,培养学生的探究意识和解决实际问题的能力.
活动
二:
实践
探究
交流
新知
1.探究新知
活动一:针对[课堂引入]的问题,教师进行提示:
①要解答二次函数的问题,必须把抛物线放在平面直角坐标系中,所以必须建立适当的平面直角坐标系;
②求水面增加的宽度,实际上就是求水面与抛物线的交点的坐标;
③求出函数解析式,进而求点的坐标;
④求函数解析式应该用待定系数法.
师生活动:学生先独立进行解答,然后小组内交流讨论,教师适时点拨,指导学生写出解题过程.
解:以抛物线的顶点为原点,对称轴为y轴,建立平面直角坐标系,如图22-3-24.根据图象的特殊性,设抛物线的函数解析式为y=ax2,由抛物线经过点A(-2,-2),可得a=-,所以抛物线的函数解析式为y=-x2.把y=-3代入函数解析式,得x=±,所以CD-AB=(2 -4)米,
则水面宽度将增加(2 -4)米.
图22-3-24
活动二:教师指导学生建立不同的平面直角坐标系进行解答.
学生独立完成解题过程,小组内交流比较:建立的平面直角坐标系是否相同,计算结果是否一致.
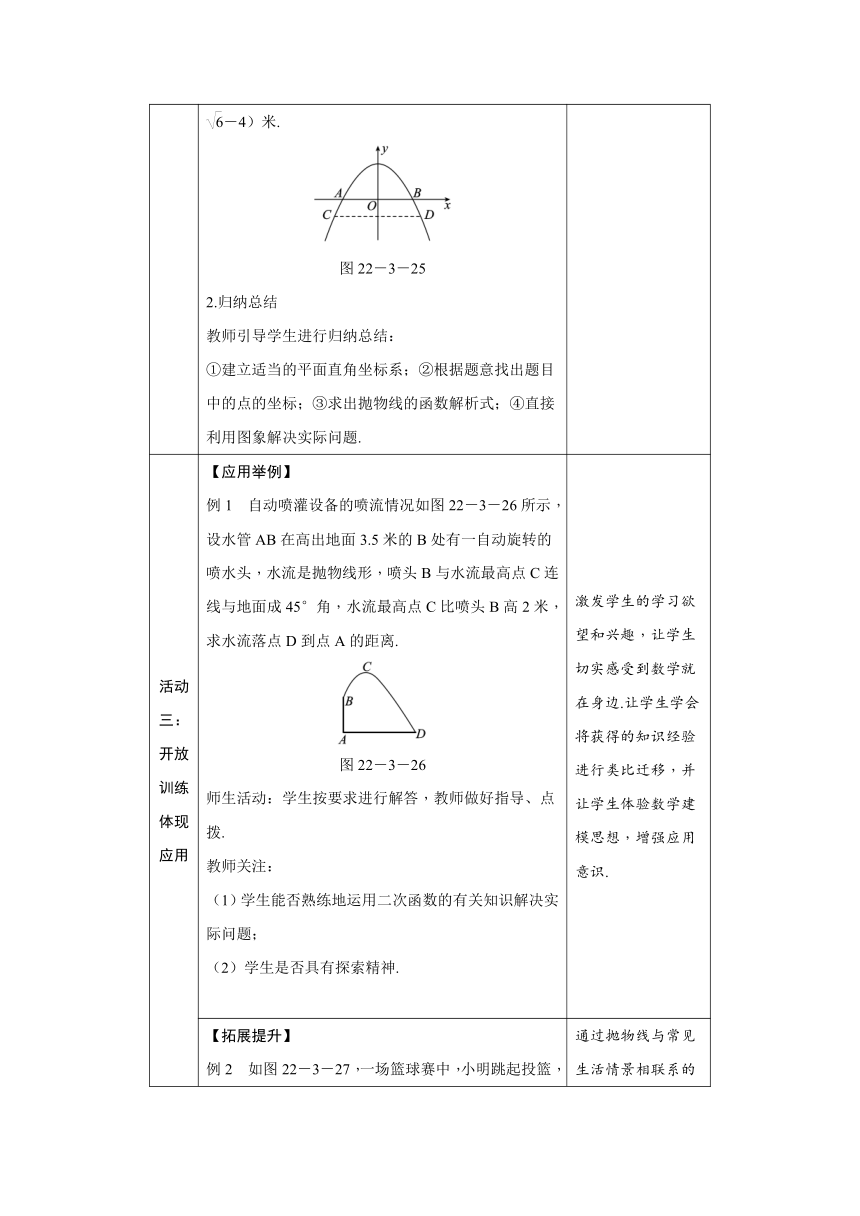
如解法:如图22-3-25,设AB所在直线为x轴,经过AB的中点O且与AB垂直的直线为y轴,则通过画图可知O为原点,抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB的长为AB长的一半,即为2米,抛物线的顶点坐标为(0,2),通过以上条件可设解析式为顶点式y=ax2+2.将点A的坐标(-2,0)代入解析式,得a=-,所以抛物线的函数解析式为y=-x2+2.把y=-1代入上式,得x=±,
所以CD-AB=米,则水面宽度将增加(2 -4)米.
图22-3-25
2.归纳总结
教师引导学生进行归纳总结:
①建立适当的平面直角坐标系;②根据题意找出题目中的点的坐标;③求出抛物线的函数解析式;④直接利用图象解决实际问题.
1.通过建立不同的平面直角坐标系得到不同的函数解析式,但结果是相同的,选择合适的平面直角坐标系可以使解答更简便,更明确易懂.
2.通过总结抛物线形实际问题的解题步骤,使学生明确问题的解答方法,思路清晰,明确解题方向.
活动
三:
开放
训练
体现
应用
【应用举例】
自动喷灌设备的喷流情况如图22-3-26所示,设水管AB在高出地面3.5米的B处有一自动旋转的喷水头,水流是抛物线形,喷头B与水流最高点C连线与地面成45°角,水流最高点C比喷头B高2米,求水流落点D到点A的距离.
图22-3-26
师生活动:学生按要求进行解答,教师做好指导、点拨.
教师关注:
(1)学生能否熟练地运用二次函数的有关知识解决实际问题;
(2)学生是否具有探索精神.
激发学生的学习欲望和兴趣,让学生切实感受到数学就在身边.让学生学会将获得的知识经验进行类比迁移,并让学生体验数学建模思想,增强应用意识.
【拓展提升】
如图22-3-27,一场篮球赛中,小明跳起投篮,已知球出手时离地面米,与篮筐中心的水平距离为7米,当球出手后水平距离为4米时达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3.05米.问此球能否投中篮筐?
图22-3-27
师生活动:学生独立解答,再合作交流,然后展示成果.教师巡视,观察学生解决问题的过程与方法,并给予学习有困难的学生及时的引导和帮助.
通过抛物线与常见生活情景相联系的题目的展示,拓宽学生视野,提高学生灵活运用知识的能力.
活动
四:
课堂
总结
反思
【达标测评】
1.如图22-3-28所示的是一学生推铅球时铅球行进高度y(m)与水平距离x(m)之间的函数图象,观察图象,则铅球推出的水平距离是 10 m.
图22-3-28 图22-3-29
2.小明以二次函数y=2x2-4x+8的图象为灵感为“北京房山国际葡萄酒大赛”设计了一款杯子,如图22-3-29为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( B )
A.14 B.11
C.6 D.3
3.某工厂的大门是一个抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高处各有一盏壁灯,
两盏壁灯之间的水平距离为6 m,如图22-3-30所示,则厂门的高约为 6.9 m (水泥建筑物厚度不计,精确到0.1 m).
图22-3-30
4.城市花园广场喷泉的喷嘴安装在平地上,有一喷嘴喷出的水流呈抛物线形,喷出水流的高度y(m)与喷出水流距喷嘴的水平距离x(m)之间满足函数解析式y=-x2+2x.
(1)求喷嘴喷出的水流的最大高度是多少;
(2)求喷嘴喷出的水流的最远距离是多少.
学生进行当堂检测,完成后,教师进行批阅、点评、讲解.
针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结:
(1)你在本节课中有哪些收获?有哪些进步?
(2)学习本节课后,还存在哪些困惑?
2.布置作业:
教材第52页习题22.3第3题.
小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在探究新知环节中,充分利用多媒体手段提高课堂效率,激发学生的学习兴趣,调动学生的学习积极性,有效解决了教学的重难点;在课堂训练环节中,教师给予学生充分的自由时间,让学生能够体会建立平面直角坐标系的作用,明确解答问题的步骤,树立建模思想.
②[讲授效果反思]
教师强调重点:(1)明确解决抛物线形问题的步骤;(2)设抛物线的函数解析式时,要根据函数图象选择恰当的形式.
③[师生互动反思]
在开放、多样的教学活动中,培养学生主动合作的意识及对数学的兴趣和爱好.
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
典案二 导学设计
学案一
学习目标:
1、体会二次函数是一类最优化问题的数学模型,了解数学的应用价值。
2、掌握实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值、最小值。
学习重点:应用二次函数最值解决实际问题中的最大利润。
学习难点:能够正确地应用二次函数最值解决实际问题中的最大利润.特别是把握好自变量的取值范围对最值的影响。
学习过程:
一、预备练习:
1. 如图,小明的父亲在相距2米的两棵树间拴了一根绳
子,给他做了一个简易的秋千,拴绳子的地方距地面高都
是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距
较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的
最低点距地面的距离为 米.
2. 一名男生推铅球,铅球行进高度false(单位:m)与水
平距离false(单位:m)之间的关系是false.
则他将铅球推出的距离是 m
二、新课导学:
1、如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?
2、某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10false米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3.6米,问此次跳水会不会失误?
第3课时 二次函数与拱桥类问题
课题
第3课时 二次函数与拱桥类问题
授课人
教
学
目
标
知识技能
1.能根据具体的问题情境建立数学模型,应用二次函数的知识求解,并根据具体问题的实际意义检验结果的合理性;
2.学会从多个角度思考问题,逐步提高解决问题的能力.
数学思考
1.通过对实际问题的研究,体会建模的数学思想;
2.经历将实际问题抽象为数学问题的过程,体会转化和数形结合的思想.
问题解决
通过问题的设计、解答,使学生学会从不同角度寻求解决问题的方法,获得解决问题的经验.
情感态度
1.通过小组合作交流,提高合作意识,培养创新精神;
2.通过用二次函数的知识解决实际问题,体会数学与现实生活的紧密联系,提高学习数学的兴趣,增强应用数学的意识.
教学重点
探究应用二次函数的知识解决实际问题的方法.
教学难点
如何从实际问题中抽象出数学问题,建立数学模型.
授课类型
新授课
课时
教具
多媒体
教学活动
教学步骤
师生活动
设计意图
回顾
1.二次函数解析式常见的形式有哪几种?并说明其特征.
2.对二次函数y=ax2+bx+c的图象进行平移时:
向上平移k(k>0)个单位长度得到的图象对应的函数解析式是什么?
向下平移k(k>0)个单位长度得到的图象对应的函数解析式是什么?
向左平移h(h>0)个单位长度得到的图象对应的函数解析式是什么?
向右平移h(h>0)个单位长度得到的图象对应的函数解析式是什么?
师生活动:教师引导学生回忆知识,学生进行解答,教师做好点评.
在已有知识的基础上提出新的问题,能为学生营造一个主动思考、探索的氛围,激发学生的学习兴趣.
活动
一:
创设
情境
导入
新课
【课堂引入】
问题:图22-3-23是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米?
图22-3-23
师生活动:
教师进行引导,提出问题:
对于本题你认为应该运用什么知识进行解答?
根据问题中的图形为抛物线,由此可知本题应该运用二次函数的知识进行解答.
学生分组讨论,如何利用函数模型解决问题,教师帮助学生解决问题.
通过日常生活中的实际问题,激发学生的学习兴趣,培养学生的探究意识和解决实际问题的能力.
活动
二:
实践
探究
交流
新知
1.探究新知
活动一:针对[课堂引入]的问题,教师进行提示:
①要解答二次函数的问题,必须把抛物线放在平面直角坐标系中,所以必须建立适当的平面直角坐标系;
②求水面增加的宽度,实际上就是求水面与抛物线的交点的坐标;
③求出函数解析式,进而求点的坐标;
④求函数解析式应该用待定系数法.
师生活动:学生先独立进行解答,然后小组内交流讨论,教师适时点拨,指导学生写出解题过程.
解:以抛物线的顶点为原点,对称轴为y轴,建立平面直角坐标系,如图22-3-24.根据图象的特殊性,设抛物线的函数解析式为y=ax2,由抛物线经过点A(-2,-2),可得a=-,所以抛物线的函数解析式为y=-x2.把y=-3代入函数解析式,得x=±,所以CD-AB=(2 -4)米,
则水面宽度将增加(2 -4)米.
图22-3-24
活动二:教师指导学生建立不同的平面直角坐标系进行解答.
学生独立完成解题过程,小组内交流比较:建立的平面直角坐标系是否相同,计算结果是否一致.
如解法:如图22-3-25,设AB所在直线为x轴,经过AB的中点O且与AB垂直的直线为y轴,则通过画图可知O为原点,抛物线以y轴为对称轴,且经过A,B两点,可求出OA和OB的长为AB长的一半,即为2米,抛物线的顶点坐标为(0,2),通过以上条件可设解析式为顶点式y=ax2+2.将点A的坐标(-2,0)代入解析式,得a=-,所以抛物线的函数解析式为y=-x2+2.把y=-1代入上式,得x=±,
所以CD-AB=米,则水面宽度将增加(2 -4)米.
图22-3-25
2.归纳总结
教师引导学生进行归纳总结:
①建立适当的平面直角坐标系;②根据题意找出题目中的点的坐标;③求出抛物线的函数解析式;④直接利用图象解决实际问题.
1.通过建立不同的平面直角坐标系得到不同的函数解析式,但结果是相同的,选择合适的平面直角坐标系可以使解答更简便,更明确易懂.
2.通过总结抛物线形实际问题的解题步骤,使学生明确问题的解答方法,思路清晰,明确解题方向.
活动
三:
开放
训练
体现
应用
【应用举例】
自动喷灌设备的喷流情况如图22-3-26所示,设水管AB在高出地面3.5米的B处有一自动旋转的喷水头,水流是抛物线形,喷头B与水流最高点C连线与地面成45°角,水流最高点C比喷头B高2米,求水流落点D到点A的距离.
图22-3-26
师生活动:学生按要求进行解答,教师做好指导、点拨.
教师关注:
(1)学生能否熟练地运用二次函数的有关知识解决实际问题;
(2)学生是否具有探索精神.
激发学生的学习欲望和兴趣,让学生切实感受到数学就在身边.让学生学会将获得的知识经验进行类比迁移,并让学生体验数学建模思想,增强应用意识.
【拓展提升】
如图22-3-27,一场篮球赛中,小明跳起投篮,已知球出手时离地面米,与篮筐中心的水平距离为7米,当球出手后水平距离为4米时达到最大高度4米.设篮球运动的轨迹为抛物线,篮筐中心距离地面3.05米.问此球能否投中篮筐?
图22-3-27
师生活动:学生独立解答,再合作交流,然后展示成果.教师巡视,观察学生解决问题的过程与方法,并给予学习有困难的学生及时的引导和帮助.
通过抛物线与常见生活情景相联系的题目的展示,拓宽学生视野,提高学生灵活运用知识的能力.
活动
四:
课堂
总结
反思
【达标测评】
1.如图22-3-28所示的是一学生推铅球时铅球行进高度y(m)与水平距离x(m)之间的函数图象,观察图象,则铅球推出的水平距离是 10 m.
图22-3-28 图22-3-29
2.小明以二次函数y=2x2-4x+8的图象为灵感为“北京房山国际葡萄酒大赛”设计了一款杯子,如图22-3-29为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( B )
A.14 B.11
C.6 D.3
3.某工厂的大门是一个抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高处各有一盏壁灯,
两盏壁灯之间的水平距离为6 m,如图22-3-30所示,则厂门的高约为 6.9 m (水泥建筑物厚度不计,精确到0.1 m).
图22-3-30
4.城市花园广场喷泉的喷嘴安装在平地上,有一喷嘴喷出的水流呈抛物线形,喷出水流的高度y(m)与喷出水流距喷嘴的水平距离x(m)之间满足函数解析式y=-x2+2x.
(1)求喷嘴喷出的水流的最大高度是多少;
(2)求喷嘴喷出的水流的最远距离是多少.
学生进行当堂检测,完成后,教师进行批阅、点评、讲解.
针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结:
(1)你在本节课中有哪些收获?有哪些进步?
(2)学习本节课后,还存在哪些困惑?
2.布置作业:
教材第52页习题22.3第3题.
小结环节的设置能够让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在探究新知环节中,充分利用多媒体手段提高课堂效率,激发学生的学习兴趣,调动学生的学习积极性,有效解决了教学的重难点;在课堂训练环节中,教师给予学生充分的自由时间,让学生能够体会建立平面直角坐标系的作用,明确解答问题的步骤,树立建模思想.
②[讲授效果反思]
教师强调重点:(1)明确解决抛物线形问题的步骤;(2)设抛物线的函数解析式时,要根据函数图象选择恰当的形式.
③[师生互动反思]
在开放、多样的教学活动中,培养学生主动合作的意识及对数学的兴趣和爱好.
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
典案二 导学设计
学案一
学习目标:
1、体会二次函数是一类最优化问题的数学模型,了解数学的应用价值。
2、掌握实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值、最小值。
学习重点:应用二次函数最值解决实际问题中的最大利润。
学习难点:能够正确地应用二次函数最值解决实际问题中的最大利润.特别是把握好自变量的取值范围对最值的影响。
学习过程:
一、预备练习:
1. 如图,小明的父亲在相距2米的两棵树间拴了一根绳
子,给他做了一个简易的秋千,拴绳子的地方距地面高都
是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距
较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的
最低点距地面的距离为 米.
2. 一名男生推铅球,铅球行进高度false(单位:m)与水
平距离false(单位:m)之间的关系是false.
则他将铅球推出的距离是 m
二、新课导学:
1、如图所示,桃河公园要建造圆形喷水池.在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m.由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.
(1)如果不计其它因素,那么水池的半径至少要多少m,才能使喷出的水流不致落到池外?
(2)若水流喷出的抛物线形状与(1)相同,水池的半径为3.5m,要使水流不落到池外,此时水流的最大高度应达到多少m(精确到0.1m)?
2、某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10false米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3.6米,问此次跳水会不会失误?
同课章节目录
