11.3 多边形及其内角和练习卷 (Word版含答案)
文档属性
| 名称 | 11.3 多边形及其内角和练习卷 (Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 08:58:58 | ||
图片预览




文档简介
11.3
多边形及其内角和练习卷普通用卷
总分:100分
班级:
姓名:
一
单选题
(共12题
,总分值36分
)
1.
已知一个多边形的内角和是540°,则这个多边形是 ( )
(3
分)
A.
四边形
B.
五边形
C.
六边形
D.
七边形
2.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为 ( )(3
分)
A.
120°
B.
110°
C.
100°
D.
40°
3.
正多边形的一个内角为135°,则该正多边形的边数为(
)
(3
分)
A.
9
B.
8
C.
7
D.
4
4.
如果n边形每一个内角等于与它相邻外角的2倍,则n的值是(
)
(3
分)
A.
4
B.
5
C.
6
D.
7
5.
如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为(
)(3
分)
A.
30°
B.
36°
C.
38°
D.
45°
6.
一个正多边形内角和等于540°,则这个正多边形的每一个外角等于(
)
(3
分)A.
72°
B.
60°
C.
108°
D.
90°.
7.
—个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为(
)
(3
分)
A.
5
B.
5或6
C.
5或7
D.
5或6或7
8.
若一个多边形的边数加1,则它的内角和( )
(3
分)
A.
不变
B.
增加180°
C.
减少180°
D.
无法确定
9.
下列多边形中,不能够单独铺满地面的是(
)
(3
分)
A.
正三角形
B.
正方形
C.
正五边形
D.
正六边形
10.
如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于(
)(3
分)
A.
90°
B.
180°
C.
210°
D.
270°
11.
如图所示,△ABC中,∠A、∠B、∠C的外角分别记为α,β,γ,若α∶β∶γ=3∶4∶5,则∠A∶∠B∶∠C=(
)(3
分)
A.
3∶2∶1
B.
1∶2∶3
C.
3∶4∶5
D.
5∶4∶3
12.
如图,∠1=27.5°,∠2=95°,∠3=38.5°,则∠4的大小是(
)(3
分)
A.
17°
B.
18°
C.
19°
D.
20°
二
填空题
(共6题
,总分值18分
)
13.
若一个正多边形的一个外角为40?,则这个正多边形是___________边形.
(3
分)
14.
从n边形的一个顶点可引出5条对角线,则这是____边形,
它共_____条对角线.
(3
分)
15.
如图,∠1是五边形ABCDE的一个外角,若∠1=65°,
则∠A+∠B+∠C+∠D=_______°.(3
分)
16.
每个内角都相等的多边形,若它的一个外角等于一个内角的
,则这个多边形的边数是________________________.
(3
分)
17.
如图,小亮从A点出发,沿直线前进10米后向左转30°,
再沿直线前进10米,又向左转30°……照这样下去,
他第一次回到出发点时,一共走了____________米.(3
分)
18.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,
∠E=80°,则∠F=________________________度。(3
分)
三
解答题(简答题)
(共7题
,总分值46分
)
19.
如图,请你根据图中信息求出x的值.(6
分)
20.
一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
(6
分)
21.
一个多边形,除一个内角外,其余各内角之和等于1000°,求这个内角及多边形的边数。
(6
分)
22.
多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.
(6
分)
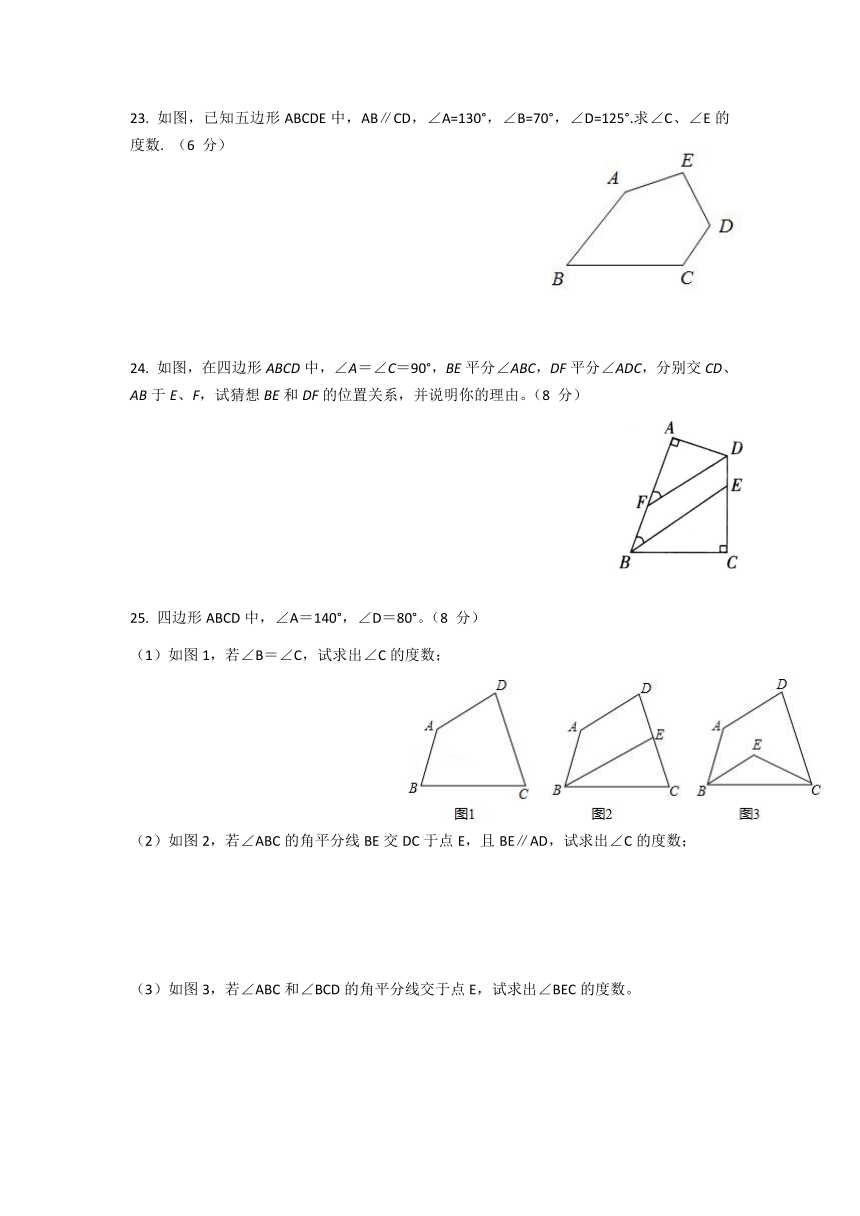
23.
如图,已知五边形ABCDE中,AB∥CD,∠A=130°,∠B=70°,∠D=125°.求∠C、∠E的度数.
(6
分)
24.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,分别交CD、AB于E、F,试猜想BE和DF的位置关系,并说明你的理由。(8
分)
25.
四边形ABCD中,∠A=140°,∠D=80°。(8
分)
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数。
一
单选题
(共12题
,总分值36分
)
1.
答案:B
解析过程:
2.
答案:C
解析过程:
3.
答案:B
解析过程:思路分析:
考点解剖:本题考查了外角和的大小与多边形的边数无关,由外角和求正多边形的边数,难度适中.
解题思路:一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数,根据任何多边形的外角和都是360度,利用360度除以外角的度数就可以求出多边形外角的个数,即多边形的边数.
解答过程:
解:∵正多边形的一个内角为135°,
∴外角是180-135=45°,
∵360÷45=8,则这个多边形是八边形,故选B.
规律总结:正多边形的所有内角都相等,所有外角都相等,外角和为360°,此类问题常用两种方法表示多边形的内角和,或者根据多边形外角和是360°这一定值来解决.
4.
答案:C
解析过程:设出外角的度数,表示出内角的度数,根据一个内角与它相邻的外角互补列出方程,解方程得到答案.
解:设外角为x,则相邻的内角为2x,
由题意得,2x+x=180°,
解得,x=60°,
360÷60°=6,
故选C.
5.
答案:B
解析过程:∵ABCDE是正五边形,
∴∠BAE=(5﹣2)×180°÷5=108°,
∵l∥BE,
∴∠1=(180°-108°)÷2=36°,
故选:B.
6.
答案:A
解析过程:解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:
=72°.
故选A.
此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n﹣2)?180°,外角和等于360°.
7.
答案:D
解析过程:设内角和为720°的多边形的边数是n,则
,解得
.则原多边形的边数为5或6或7.
8.
答案:B
解析过程:
9.
答案:C
解析过程:思路分析:
考点解剖:几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
解题思路:由镶嵌的条件知,在一个顶点处各个内角和为360°.
解答过程:
解:正三角形每个内角60°,6×60°=360°;正方形每个内角90°,4×90°=360°;正六边形每个内角120°,3×120°=360°;所以这3种多边形能够单独铺满地面,而正五边形每个内角108°,几个正五边形不能铺成360°,就不能够单独铺满地面.(用一种正多边形镶嵌,只有正三角形,正方形,正六边形三种正多边形能镶嵌成一个平面图案).
∴不能铺满地面的是正五边形
故选C.
规律总结:用形状、大小完全相同或不同的一种或几种的平面图形进行拼接,彼此间不留空隙,不重叠地铺成一片,就叫做图形的镶嵌,也叫做图形的密铺.
10.
答案:B
解析过程:∵AB∥CD,∴∠B+∠C=180°,∴∠B、∠C两角的外角和是180°,∵五边形外角和是360°,∴∠1+∠2+∠3=360°-180°=180°,故选B。
11.
答案:A
解析过程:三角形的外角和是360°,设α、β、γ分别为3x°、4x°、5x°,则3x+4x+5x=360,解得x=30,所以α=90°、β=120°、γ=150°,∠A=90°,∠B=60°,∠C=30°,所以∠A∶∠B∶∠C=3∶2∶1。
12.
答案:C
解析过程:思路分析:
认真观察图形找到四个角之间的关系,根据已知求出∠4的大小.
解答过程:
因为∠1+∠4=180°-(∠2+∠3),
所以∠4=180°-(∠1+∠2+∠3)=180°-(27.5°+95°+38.5°)=19°.
拓展提升:
综合应用三角形的内角和定理及三角形外角的性质解题.
二
填空题
(共6题
,总分值18分
)
13.
答案:9
解析过程:思路分析:
考点解剖:本题考查了外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握,比较简单.
解题思路:根据任何多边形的外角和都是360度,利用多边形每一个外角都是相等的,即可求多边形的边数.
解答过程:
解:360÷40=9,即这个多边形的边数是9,
故答案为9.
规律总结:根据外角和与外角的度数的来确定正多边形的边数
14.
答案:8,20
解析过程:
15.
答案:425
解析过程:根据补角的定义得到∠AED=115°,根据五边形的内角和即可得到结论.
解:∵∠1=65°,
∴∠AED=115°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=425°,
16.
答案:5
解析过程: 设一个外角为x,则一个内角为
,故
,解得x=72°,又由任意多边形的外角和等于360°,得这个多边形的边数
.
17.
答案:120
解析过程:小亮从出发到第一次回到出发地点所走的路线可构成一个多边形,因为每个外角都为30°,所以该多边形的边数为
,所以他第一次回到出发地点时,一共走了
(米).
18.
答案:134
解析过程:解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°∵AB⊥BC,∴∠B=90°,又∵∠C=124°,∴∠BAD+∠ADC=360°-124°-90°=146°,∵CD∥AF,∴∠CDA=∠DAF,在四边形ADEF中,∵∠ADE+∠DAF=360°-∠C-∠B=360°-(124°+90°)=146°,∠DAF+∠EDA+∠F+∠E=360°,∴∠F+∠E=214°,又∵∠E=80°,∴∠F=134°,故答案为134。
三
解答题(简答题)
(共7题
,总分值46分
)
19.
答案:由题意可得:90+(2x+25)+(3x-15)十2x+x=(5-2)×180.解得x=55.
解析过程:
20.
答案:10
解析过程:设这个多边形有n条边.
由题意得:(n-2)×180°=360°×4,
解得n=10.
所以这个多边形的边数是10
21.
答案:80°、8
解析过程:分析:n边形的内角和是(n-2)?180°,因而内角和一定是180度的倍数,而多边形的内角一定大于0,并且小于180度,因而内角和除去一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1,则用内角和除去一个内角的值除以180所得值,加上2,比这个数大的最小的整数就是多边形的边数.
解:设(x-2)?180=1000,
解得x=7
,因而多边形的边数是8.
则内角和是(8-2)180=1080度,因而这个内角是1080-1000=80度.
22.
答案:
.
解析过程:此题的难点是题目中出现了一个似乎难确定的外角度数,因为内角和有公式
可用,矛盾就集中在如何将这个外角确定出来,然后利用方程(或不等式)进行求解.
解法1:设这个多边形的边数为n,这个外角的度数为x°,则
,依题意有:
,
所以
,
.
因为n为正整数,所以
必为180°的整数倍.
又
,所以
,
.
解法2:由
,
得
,
即
.
又
,
所以
,即
.
而n为正整数,所以
.
点拨:解法1是用方程来解的.解法2是利用不等式确,数范围,然后再通过边数为整数来确定的.
23.
答案:∵AB∥CD,∠B=70°,
∴∠C=180°-∠B=110°.
∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴在五边形ABCDE中,∠E=
540°-130°-70°-110°-125°=105°.
故∠C的度数是110°,∠E的度数是105°.
解析过程:
24.
答案:见解析
解析过程:BE∥DF。
∵∠ABC+∠ADC=360°-∠A-∠C=180°。
又BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠ADF=
∠ABC+
∠ADC
=
×180°=90°。
由∠A=90°可得∠AFD+∠ADF=90°,
从而∠ABE=∠AFD。∴BE∥DF。
25.
答案:见解析
解析过程:(1)因为∠A+∠B+∠C+∠D=360°,∠B=∠C,
所以∠B=∠C=
。
(2)∵BE∥AD,
∴∠BEC=∠D=80°,
∠ABE=180°-∠A=180°-140°=40°。
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°,
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°。
或解:∵BE∥AD,
∴∠ABE=180°-∠A=180°-140°=40°,
又∵BE平分∠ABC,
∴∠ABC=2∠ABE=80°,
∴∠C=360°-∠ABC-∠A-∠D=60°。
(3)∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°。
∵∠EBC=
∠ABC,∠BCE=
∠BCD,
∴∠E=180-∠EBC-∠BCE=180°-
(∠ABC+∠BCD)=180°-
×140°=110°
多边形及其内角和练习卷普通用卷
总分:100分
班级:
姓名:
一
单选题
(共12题
,总分值36分
)
1.
已知一个多边形的内角和是540°,则这个多边形是 ( )
(3
分)
A.
四边形
B.
五边形
C.
六边形
D.
七边形
2.
如图,在四边形ABCD中,若∠A+∠B+∠C=260°,则∠D的度数为 ( )(3
分)
A.
120°
B.
110°
C.
100°
D.
40°
3.
正多边形的一个内角为135°,则该正多边形的边数为(
)
(3
分)
A.
9
B.
8
C.
7
D.
4
4.
如果n边形每一个内角等于与它相邻外角的2倍,则n的值是(
)
(3
分)
A.
4
B.
5
C.
6
D.
7
5.
如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为(
)(3
分)
A.
30°
B.
36°
C.
38°
D.
45°
6.
一个正多边形内角和等于540°,则这个正多边形的每一个外角等于(
)
(3
分)A.
72°
B.
60°
C.
108°
D.
90°.
7.
—个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为(
)
(3
分)
A.
5
B.
5或6
C.
5或7
D.
5或6或7
8.
若一个多边形的边数加1,则它的内角和( )
(3
分)
A.
不变
B.
增加180°
C.
减少180°
D.
无法确定
9.
下列多边形中,不能够单独铺满地面的是(
)
(3
分)
A.
正三角形
B.
正方形
C.
正五边形
D.
正六边形
10.
如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于(
)(3
分)
A.
90°
B.
180°
C.
210°
D.
270°
11.
如图所示,△ABC中,∠A、∠B、∠C的外角分别记为α,β,γ,若α∶β∶γ=3∶4∶5,则∠A∶∠B∶∠C=(
)(3
分)
A.
3∶2∶1
B.
1∶2∶3
C.
3∶4∶5
D.
5∶4∶3
12.
如图,∠1=27.5°,∠2=95°,∠3=38.5°,则∠4的大小是(
)(3
分)
A.
17°
B.
18°
C.
19°
D.
20°
二
填空题
(共6题
,总分值18分
)
13.
若一个正多边形的一个外角为40?,则这个正多边形是___________边形.
(3
分)
14.
从n边形的一个顶点可引出5条对角线,则这是____边形,
它共_____条对角线.
(3
分)
15.
如图,∠1是五边形ABCDE的一个外角,若∠1=65°,
则∠A+∠B+∠C+∠D=_______°.(3
分)
16.
每个内角都相等的多边形,若它的一个外角等于一个内角的
,则这个多边形的边数是________________________.
(3
分)
17.
如图,小亮从A点出发,沿直线前进10米后向左转30°,
再沿直线前进10米,又向左转30°……照这样下去,
他第一次回到出发点时,一共走了____________米.(3
分)
18.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,
∠E=80°,则∠F=________________________度。(3
分)
三
解答题(简答题)
(共7题
,总分值46分
)
19.
如图,请你根据图中信息求出x的值.(6
分)
20.
一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
(6
分)
21.
一个多边形,除一个内角外,其余各内角之和等于1000°,求这个内角及多边形的边数。
(6
分)
22.
多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.
(6
分)
23.
如图,已知五边形ABCDE中,AB∥CD,∠A=130°,∠B=70°,∠D=125°.求∠C、∠E的度数.
(6
分)
24.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,分别交CD、AB于E、F,试猜想BE和DF的位置关系,并说明你的理由。(8
分)
25.
四边形ABCD中,∠A=140°,∠D=80°。(8
分)
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数。
一
单选题
(共12题
,总分值36分
)
1.
答案:B
解析过程:
2.
答案:C
解析过程:
3.
答案:B
解析过程:思路分析:
考点解剖:本题考查了外角和的大小与多边形的边数无关,由外角和求正多边形的边数,难度适中.
解题思路:一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数,根据任何多边形的外角和都是360度,利用360度除以外角的度数就可以求出多边形外角的个数,即多边形的边数.
解答过程:
解:∵正多边形的一个内角为135°,
∴外角是180-135=45°,
∵360÷45=8,则这个多边形是八边形,故选B.
规律总结:正多边形的所有内角都相等,所有外角都相等,外角和为360°,此类问题常用两种方法表示多边形的内角和,或者根据多边形外角和是360°这一定值来解决.
4.
答案:C
解析过程:设出外角的度数,表示出内角的度数,根据一个内角与它相邻的外角互补列出方程,解方程得到答案.
解:设外角为x,则相邻的内角为2x,
由题意得,2x+x=180°,
解得,x=60°,
360÷60°=6,
故选C.
5.
答案:B
解析过程:∵ABCDE是正五边形,
∴∠BAE=(5﹣2)×180°÷5=108°,
∵l∥BE,
∴∠1=(180°-108°)÷2=36°,
故选:B.
6.
答案:A
解析过程:解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:
=72°.
故选A.
此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n﹣2)?180°,外角和等于360°.
7.
答案:D
解析过程:设内角和为720°的多边形的边数是n,则
,解得
.则原多边形的边数为5或6或7.
8.
答案:B
解析过程:
9.
答案:C
解析过程:思路分析:
考点解剖:几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
解题思路:由镶嵌的条件知,在一个顶点处各个内角和为360°.
解答过程:
解:正三角形每个内角60°,6×60°=360°;正方形每个内角90°,4×90°=360°;正六边形每个内角120°,3×120°=360°;所以这3种多边形能够单独铺满地面,而正五边形每个内角108°,几个正五边形不能铺成360°,就不能够单独铺满地面.(用一种正多边形镶嵌,只有正三角形,正方形,正六边形三种正多边形能镶嵌成一个平面图案).
∴不能铺满地面的是正五边形
故选C.
规律总结:用形状、大小完全相同或不同的一种或几种的平面图形进行拼接,彼此间不留空隙,不重叠地铺成一片,就叫做图形的镶嵌,也叫做图形的密铺.
10.
答案:B
解析过程:∵AB∥CD,∴∠B+∠C=180°,∴∠B、∠C两角的外角和是180°,∵五边形外角和是360°,∴∠1+∠2+∠3=360°-180°=180°,故选B。
11.
答案:A
解析过程:三角形的外角和是360°,设α、β、γ分别为3x°、4x°、5x°,则3x+4x+5x=360,解得x=30,所以α=90°、β=120°、γ=150°,∠A=90°,∠B=60°,∠C=30°,所以∠A∶∠B∶∠C=3∶2∶1。
12.
答案:C
解析过程:思路分析:
认真观察图形找到四个角之间的关系,根据已知求出∠4的大小.
解答过程:
因为∠1+∠4=180°-(∠2+∠3),
所以∠4=180°-(∠1+∠2+∠3)=180°-(27.5°+95°+38.5°)=19°.
拓展提升:
综合应用三角形的内角和定理及三角形外角的性质解题.
二
填空题
(共6题
,总分值18分
)
13.
答案:9
解析过程:思路分析:
考点解剖:本题考查了外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握,比较简单.
解题思路:根据任何多边形的外角和都是360度,利用多边形每一个外角都是相等的,即可求多边形的边数.
解答过程:
解:360÷40=9,即这个多边形的边数是9,
故答案为9.
规律总结:根据外角和与外角的度数的来确定正多边形的边数
14.
答案:8,20
解析过程:
15.
答案:425
解析过程:根据补角的定义得到∠AED=115°,根据五边形的内角和即可得到结论.
解:∵∠1=65°,
∴∠AED=115°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=425°,
16.
答案:5
解析过程: 设一个外角为x,则一个内角为
,故
,解得x=72°,又由任意多边形的外角和等于360°,得这个多边形的边数
.
17.
答案:120
解析过程:小亮从出发到第一次回到出发地点所走的路线可构成一个多边形,因为每个外角都为30°,所以该多边形的边数为
,所以他第一次回到出发地点时,一共走了
(米).
18.
答案:134
解析过程:解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°∵AB⊥BC,∴∠B=90°,又∵∠C=124°,∴∠BAD+∠ADC=360°-124°-90°=146°,∵CD∥AF,∴∠CDA=∠DAF,在四边形ADEF中,∵∠ADE+∠DAF=360°-∠C-∠B=360°-(124°+90°)=146°,∠DAF+∠EDA+∠F+∠E=360°,∴∠F+∠E=214°,又∵∠E=80°,∴∠F=134°,故答案为134。
三
解答题(简答题)
(共7题
,总分值46分
)
19.
答案:由题意可得:90+(2x+25)+(3x-15)十2x+x=(5-2)×180.解得x=55.
解析过程:
20.
答案:10
解析过程:设这个多边形有n条边.
由题意得:(n-2)×180°=360°×4,
解得n=10.
所以这个多边形的边数是10
21.
答案:80°、8
解析过程:分析:n边形的内角和是(n-2)?180°,因而内角和一定是180度的倍数,而多边形的内角一定大于0,并且小于180度,因而内角和除去一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1,则用内角和除去一个内角的值除以180所得值,加上2,比这个数大的最小的整数就是多边形的边数.
解:设(x-2)?180=1000,
解得x=7
,因而多边形的边数是8.
则内角和是(8-2)180=1080度,因而这个内角是1080-1000=80度.
22.
答案:
.
解析过程:此题的难点是题目中出现了一个似乎难确定的外角度数,因为内角和有公式
可用,矛盾就集中在如何将这个外角确定出来,然后利用方程(或不等式)进行求解.
解法1:设这个多边形的边数为n,这个外角的度数为x°,则
,依题意有:
,
所以
,
.
因为n为正整数,所以
必为180°的整数倍.
又
,所以
,
.
解法2:由
,
得
,
即
.
又
,
所以
,即
.
而n为正整数,所以
.
点拨:解法1是用方程来解的.解法2是利用不等式确,数范围,然后再通过边数为整数来确定的.
23.
答案:∵AB∥CD,∠B=70°,
∴∠C=180°-∠B=110°.
∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴在五边形ABCDE中,∠E=
540°-130°-70°-110°-125°=105°.
故∠C的度数是110°,∠E的度数是105°.
解析过程:
24.
答案:见解析
解析过程:BE∥DF。
∵∠ABC+∠ADC=360°-∠A-∠C=180°。
又BE平分∠ABC,DF平分∠ADC,
∴∠ABE+∠ADF=
∠ABC+
∠ADC
=
×180°=90°。
由∠A=90°可得∠AFD+∠ADF=90°,
从而∠ABE=∠AFD。∴BE∥DF。
25.
答案:见解析
解析过程:(1)因为∠A+∠B+∠C+∠D=360°,∠B=∠C,
所以∠B=∠C=
。
(2)∵BE∥AD,
∴∠BEC=∠D=80°,
∠ABE=180°-∠A=180°-140°=40°。
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°,
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°。
或解:∵BE∥AD,
∴∠ABE=180°-∠A=180°-140°=40°,
又∵BE平分∠ABC,
∴∠ABC=2∠ABE=80°,
∴∠C=360°-∠ABC-∠A-∠D=60°。
(3)∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D=360°-140°-80°=140°。
∵∠EBC=
∠ABC,∠BCE=
∠BCD,
∴∠E=180-∠EBC-∠BCE=180°-
(∠ABC+∠BCD)=180°-
×140°=110°
