人教版八年级上册数学:14.2.1平方差公式 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册数学:14.2.1平方差公式 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
平方差公式
§14.2.1
计算下列多项式的积:
(x+1)(x-1)
=
(m+2)(m-2)
=
(2x+1)(2x-1)
=
x2
-
1
m2
-
4
4x2
-
1
问题:(1)你能得到结果吗?比一比,谁最快,你从中有什么发现?请将结果作以汇报。
(2)你能写出几个与习题同类型式子吗?得到什么样的结果呢?与你的发现规律一致吗?
(a+b)(a-b)
=
猜想:
a2-b2
相信你一定可以得到它的结果。你能验证吗?
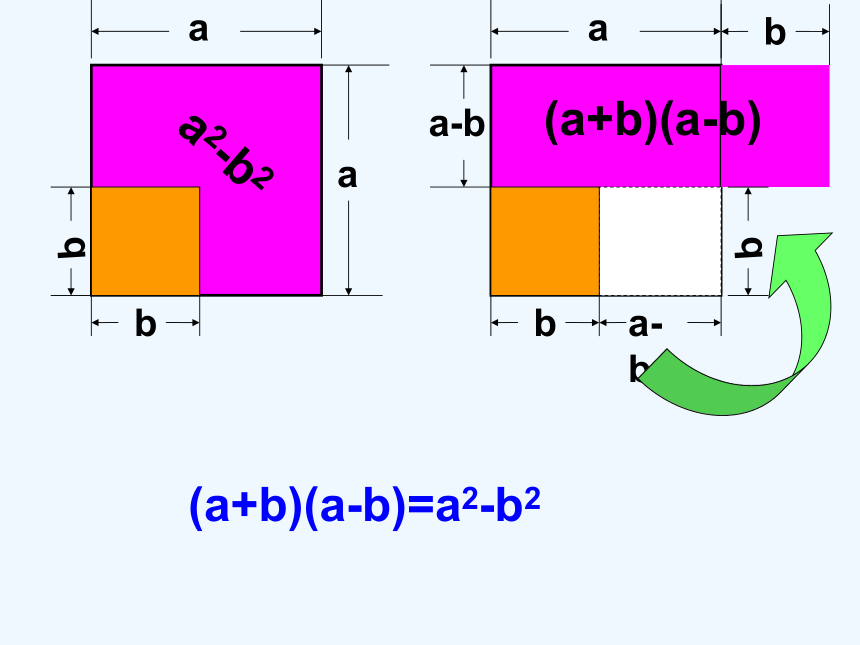
活动二、数形验证 把握公式
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
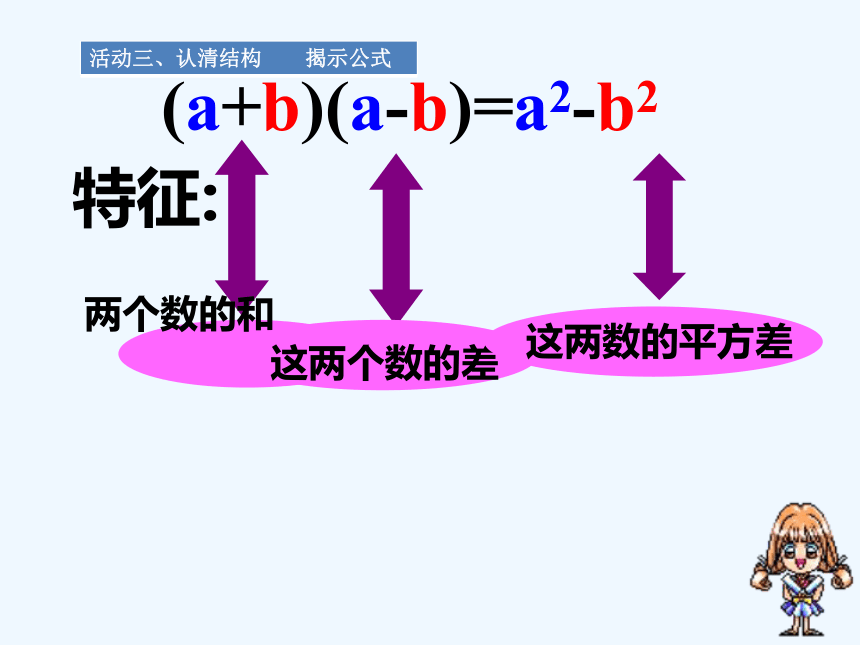
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
活动三、认清结构 揭示公式
(a+b)(a-b)=a2-b2
两个数的和
与这两个数的差的积,
等于这两个数的平方差。
平方差公式
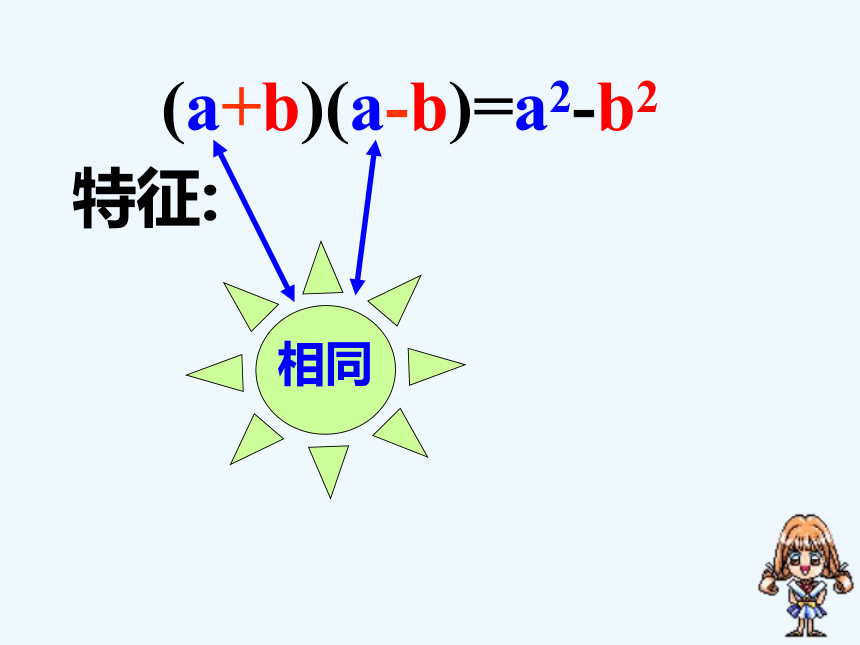
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
选择
下列各式中,能用平方差公式运算的有
(1)(x-2y)(2y+x)
(2)(-3x+2y)(-3x-2y)
(3)(2a-3b)(3a+2b)
(4)(a+b+c)(b+a-c)
例1
运用平方差公式计算:
⑴
(3x+2)(3x-2)
;
⑵
(b+2a)(2a-b);
(3)
(-x+2y)(-x-2y).
活动四、示例应用 巩固公式
ㄨ
判断
下面各式的计算对不对?
如果不对,应当怎样改正?
(1)
(x+2)(x-2)
=
x2
-
2
(2)
(-3a-2)(3a-2)
=
9a2
-
4
X2
-
4
ㄨ
4
-
9a2
小试牛刀
例2
计算:
⑴
102
×98;
⑵
(y+2)(y-2)-(y-1)(y+5);
⑴
102
×98
动
脑筋!
谁是a?
谁是b?
102
=
(100+2)
98
(100-2)
=
1002-22
=
10000-4
=
9996
谈谈你的学习心得
(a+b)(a-b)=a2-b2
两个数的和
与这两个数的差的积,
等于这两个数的平方差。
小结:
作业:课本P108
第1,2题,
平方差公式
§14.2.1
计算下列多项式的积:
(x+1)(x-1)
=
(m+2)(m-2)
=
(2x+1)(2x-1)
=
x2
-
1
m2
-
4
4x2
-
1
问题:(1)你能得到结果吗?比一比,谁最快,你从中有什么发现?请将结果作以汇报。
(2)你能写出几个与习题同类型式子吗?得到什么样的结果呢?与你的发现规律一致吗?
(a+b)(a-b)
=
猜想:
a2-b2
相信你一定可以得到它的结果。你能验证吗?
活动二、数形验证 把握公式
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
活动三、认清结构 揭示公式
(a+b)(a-b)=a2-b2
两个数的和
与这两个数的差的积,
等于这两个数的平方差。
平方差公式
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
选择
下列各式中,能用平方差公式运算的有
(1)(x-2y)(2y+x)
(2)(-3x+2y)(-3x-2y)
(3)(2a-3b)(3a+2b)
(4)(a+b+c)(b+a-c)
例1
运用平方差公式计算:
⑴
(3x+2)(3x-2)
;
⑵
(b+2a)(2a-b);
(3)
(-x+2y)(-x-2y).
活动四、示例应用 巩固公式
ㄨ
判断
下面各式的计算对不对?
如果不对,应当怎样改正?
(1)
(x+2)(x-2)
=
x2
-
2
(2)
(-3a-2)(3a-2)
=
9a2
-
4
X2
-
4
ㄨ
4
-
9a2
小试牛刀
例2
计算:
⑴
102
×98;
⑵
(y+2)(y-2)-(y-1)(y+5);
⑴
102
×98
动
脑筋!
谁是a?
谁是b?
102
=
(100+2)
98
(100-2)
=
1002-22
=
10000-4
=
9996
谈谈你的学习心得
(a+b)(a-b)=a2-b2
两个数的和
与这两个数的差的积,
等于这两个数的平方差。
小结:
作业:课本P108
第1,2题,
