第二章 有理数及其运算 章末复习 课件(共44张PPT)
文档属性
| 名称 | 第二章 有理数及其运算 章末复习 课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 20:49:22 | ||
图片预览











文档简介
(共44张PPT)
北师大版·七年级上册
章末复习
学习目标
【知识与技能】
掌握本章主要知识,会求一个数的相反数和绝对值、倒数,会比较有理数的大小,能灵活运用计算法则和运算律进行有理数的运算.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想、分类讨论思想、转化思想,加深对本章知识的理解
【情感态度】
在运用本章知识解决具体问题过程中,进一步体会数学与生活的密切联系,增强数学应用意识,激发学生学习兴趣.
【教学重点】
回顾本章知识点,构建知识体系.
【教学难点】
利用有理数的相关知识解决实际问题.
一、有理数的基本概念
1.负数
2.有理数
3.数轴
4.相反数
5.倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法
1.负数
在正数前面加“-”的数;
0
既不是正数,也不是负数.
整数和分数统称有理数.
2.有理数
(
)数
(
)数
(
)
(
)
(
)
(
)
(
)
有理数
正整数
零
负整数
正分数
负分数
整
分
下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:
练习
负数集合
整数集合
3.数轴
规定了原点、正方向和单位长度的直线.
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
(1)在数轴上表示的两个数,右边的数总比左边的数大;
(2)正数都大于0,负数都小于0;正数大于一切负数;
(3)所有有理数都可以用数轴上的点表示.
4.相反数
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数.
-4
-3
-2
-1
0
1
2
3
4
(1)数a的相反数是-a(a是任意一个有理数);
(2)0的相反数是0;
(3)若a、b互为相反数,则
a+b
=
0.
5.倒数
如果两个有理数的乘积为1,那么称其中的一个数是另一个数的倒数.
(1)a
的倒数是
(a
≠
0);
(3)若
a
与
b
互为倒数,则
ab
=
1.
(2)0没有倒数
;
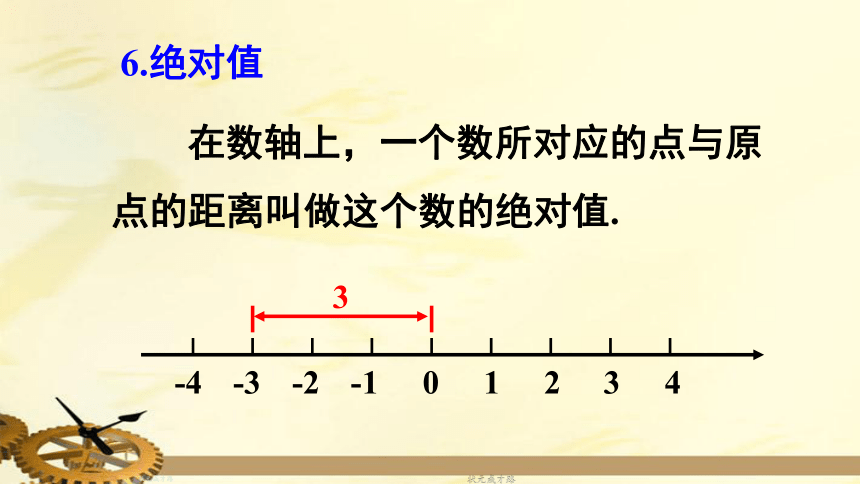
6.绝对值
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.
-4
-3
-2
-1
0
1
2
3
4
3
若
a>0,则︱a︱=
____;
若
a<0,则︱a︱=
____;
若
a
=
0,则︱a︱=
____.
a
(1)
-a
0
(2)对任何有理数
a,总有︱a︱≥0.
7.有理数的大小比较
(1)利用数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数.
(2)利用绝对值比较
两个负数比较大小,绝对值大的反而小.
若
a<0,b<0,且︱a︱>︱b︱,则a
<
b.
一般地,一个大于
10
的数可以表示成
a×10n
的形式,其中
1
≤
a
<
10,n
是正整数,这种记数方法叫做科学记数法.
8.科学记数法
55
000
000
=
5.5×107
巩固练习
1.下表记录了某星期内股市的涨跌情况,请完成下表:
-50
+60
-30
+2
2.用数轴上的点表示下列各有理数,并求其相反数和绝对值:
-
0.5,
-
3.5,7,
-
4.5,
-
4.
-4
-3
-2
-1
0
1
2
3
4
-5
5
6
7
-
0.5
-
3.5
-
4.5
-
4
7
-
0.5,
-
3.5,7,
-
4.5,
-
4.
-
0.5的相反数是0.5,绝对值是0.5;
-
3.5的相反数是3.5,绝对值是3.5;
7的相反数是-7,绝对值是7;
-
4.5的相反数是4.5,绝对值是4.5;
-
4的相反数是4,绝对值是4;
3.下列说法是否正确?请将错误的改正过来.
(1)所有的有理数都能用数轴上的点表示;
(2)符号不同的两个数互为相反数;
√
×
符号不同且绝对值相等的两个数互为相反数.
(3)有理数分为正数和负数;
(4)两数相加,和一定大于任何一个加数;
(5)两数相减,差一定小于被减数.
×
有理数分为正有理数、负有理数和零.
×
两数相加,和不一定大于任何一个加数.
×
两数相减,差不一定小于被减数.
4.写出符合下列条件的数:
(1)最小的正整数;
(2)最大的负整数;
(3)大于
-
3
且小于
2
的所有整数;
1
-1
-2,-1,0,1
(4)绝对值最小的有理数;
(5)绝对值大于
2
且小于
5
的所有负整数;
(6)在数轴上,与表示
-
1
的点的距离为
2
的所有数.
0
-3和-4
-3和1
天体名称
围绕太阳公转的轨道半长径/km
科学记数法
水星
58
000
000
金星
110
000
000
地球
150
000
000
火星
230
000
000
5.请用科学记数法表示下表中的数据:
5.8×107
1.1×108
1.5×108
2.3×108
二、有理数的运算
1.有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
若a>0,b>0,则
a
+
b
=
|a|
+
|b|
若a<0,b<0,则
a
+
b
=
-(
|a|
+
|b|
)
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
若a>0,b<0,|a|
>
|b|,则a
+
b
=
|a|
+
|b|.
若a>0,b<0,|a|
<
|b|,则a
+
b
=
-(|b|
-
|a|).
(3)一个数同0相加,仍得这个数.
a
是任一个有理数,则
a
+
0
=
a
2.有理数减法法则
减去一个数,等于加上这个数的相反数.
a
-
b
=
a
+
(
-
b
)
3.有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,积仍为0.
若a>0,b>0,则
ab
=
+|a|×|b|.
若a<0,b<0,则
ab
=
+|a|×|b|.
若a>0,b<0,则
ab
=
-|a|×|b|.
若a<0,b>0,则
ab
=
-|a|×|b|.
同号
异号
4.有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0.
除以一个数等于乘上这个数的倒数.
a÷b
=
a×
(b
≠
0)
5.有理数的乘方
求
n
个相同因数
a
的积的运算叫做乘方.
a×a
×…
×a
×a
n个a
=
an
正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数.
混合运算
先算乘方,再算乘除,最后算加减,如果有括号,先算括号里面的.
有理数的运算律
加法交换律
a
+
b
=
b
+
a
加法结合律
(a
+
b
)
+
c
=
a
+
(
b
+
c
)
乘法交换律
乘法结合律
ab
=
ba
(ab)c=a(bc)
乘法对加法的分配律
a(
b
+
c
)
=
ab
+
ac
随堂练习
1.计算:
解:
解:
解:
2.某商店去年四个季度盈亏情况如下(盈余为正):+128.5
万元、
-
140
万元、
-
95.5
万元、
+280
万元.这个商店去年总的盈亏情况如何?
128.5
+
(-140)
+
(-95.5)
+
280
=
173(万元)
答:盈余173万元.
3.小明记录了本小组同学的身高(单位:cm):
158,163,154,160,165,162
,157,160.
请你计算这个小组同学的平均身高.
158,163,154,160,165,162
,157,160.
解:以
160
cm
为标准身高,则小组同学的身高与标准身高的差分别是
-2
3
-6
0
5
2
-3
0
(-2+3-6+0+5+2-3+0)÷8+160
=
159.875(cm)
答:这组同学的平均身高是159.875
cm.
课堂小结
通过这节课的学习活动,你有什么收获?
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
北师大版·七年级上册
章末复习
学习目标
【知识与技能】
掌握本章主要知识,会求一个数的相反数和绝对值、倒数,会比较有理数的大小,能灵活运用计算法则和运算律进行有理数的运算.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想、分类讨论思想、转化思想,加深对本章知识的理解
【情感态度】
在运用本章知识解决具体问题过程中,进一步体会数学与生活的密切联系,增强数学应用意识,激发学生学习兴趣.
【教学重点】
回顾本章知识点,构建知识体系.
【教学难点】
利用有理数的相关知识解决实际问题.
一、有理数的基本概念
1.负数
2.有理数
3.数轴
4.相反数
5.倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法
1.负数
在正数前面加“-”的数;
0
既不是正数,也不是负数.
整数和分数统称有理数.
2.有理数
(
)数
(
)数
(
)
(
)
(
)
(
)
(
)
有理数
正整数
零
负整数
正分数
负分数
整
分
下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:
练习
负数集合
整数集合
3.数轴
规定了原点、正方向和单位长度的直线.
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
(1)在数轴上表示的两个数,右边的数总比左边的数大;
(2)正数都大于0,负数都小于0;正数大于一切负数;
(3)所有有理数都可以用数轴上的点表示.
4.相反数
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数.
-4
-3
-2
-1
0
1
2
3
4
(1)数a的相反数是-a(a是任意一个有理数);
(2)0的相反数是0;
(3)若a、b互为相反数,则
a+b
=
0.
5.倒数
如果两个有理数的乘积为1,那么称其中的一个数是另一个数的倒数.
(1)a
的倒数是
(a
≠
0);
(3)若
a
与
b
互为倒数,则
ab
=
1.
(2)0没有倒数
;
6.绝对值
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.
-4
-3
-2
-1
0
1
2
3
4
3
若
a>0,则︱a︱=
____;
若
a<0,则︱a︱=
____;
若
a
=
0,则︱a︱=
____.
a
(1)
-a
0
(2)对任何有理数
a,总有︱a︱≥0.
7.有理数的大小比较
(1)利用数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数.
(2)利用绝对值比较
两个负数比较大小,绝对值大的反而小.
若
a<0,b<0,且︱a︱>︱b︱,则a
<
b.
一般地,一个大于
10
的数可以表示成
a×10n
的形式,其中
1
≤
a
<
10,n
是正整数,这种记数方法叫做科学记数法.
8.科学记数法
55
000
000
=
5.5×107
巩固练习
1.下表记录了某星期内股市的涨跌情况,请完成下表:
-50
+60
-30
+2
2.用数轴上的点表示下列各有理数,并求其相反数和绝对值:
-
0.5,
-
3.5,7,
-
4.5,
-
4.
-4
-3
-2
-1
0
1
2
3
4
-5
5
6
7
-
0.5
-
3.5
-
4.5
-
4
7
-
0.5,
-
3.5,7,
-
4.5,
-
4.
-
0.5的相反数是0.5,绝对值是0.5;
-
3.5的相反数是3.5,绝对值是3.5;
7的相反数是-7,绝对值是7;
-
4.5的相反数是4.5,绝对值是4.5;
-
4的相反数是4,绝对值是4;
3.下列说法是否正确?请将错误的改正过来.
(1)所有的有理数都能用数轴上的点表示;
(2)符号不同的两个数互为相反数;
√
×
符号不同且绝对值相等的两个数互为相反数.
(3)有理数分为正数和负数;
(4)两数相加,和一定大于任何一个加数;
(5)两数相减,差一定小于被减数.
×
有理数分为正有理数、负有理数和零.
×
两数相加,和不一定大于任何一个加数.
×
两数相减,差不一定小于被减数.
4.写出符合下列条件的数:
(1)最小的正整数;
(2)最大的负整数;
(3)大于
-
3
且小于
2
的所有整数;
1
-1
-2,-1,0,1
(4)绝对值最小的有理数;
(5)绝对值大于
2
且小于
5
的所有负整数;
(6)在数轴上,与表示
-
1
的点的距离为
2
的所有数.
0
-3和-4
-3和1
天体名称
围绕太阳公转的轨道半长径/km
科学记数法
水星
58
000
000
金星
110
000
000
地球
150
000
000
火星
230
000
000
5.请用科学记数法表示下表中的数据:
5.8×107
1.1×108
1.5×108
2.3×108
二、有理数的运算
1.有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
若a>0,b>0,则
a
+
b
=
|a|
+
|b|
若a<0,b<0,则
a
+
b
=
-(
|a|
+
|b|
)
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
若a>0,b<0,|a|
>
|b|,则a
+
b
=
|a|
+
|b|.
若a>0,b<0,|a|
<
|b|,则a
+
b
=
-(|b|
-
|a|).
(3)一个数同0相加,仍得这个数.
a
是任一个有理数,则
a
+
0
=
a
2.有理数减法法则
减去一个数,等于加上这个数的相反数.
a
-
b
=
a
+
(
-
b
)
3.有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,积仍为0.
若a>0,b>0,则
ab
=
+|a|×|b|.
若a<0,b<0,则
ab
=
+|a|×|b|.
若a>0,b<0,则
ab
=
-|a|×|b|.
若a<0,b>0,则
ab
=
-|a|×|b|.
同号
异号
4.有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0.
除以一个数等于乘上这个数的倒数.
a÷b
=
a×
(b
≠
0)
5.有理数的乘方
求
n
个相同因数
a
的积的运算叫做乘方.
a×a
×…
×a
×a
n个a
=
an
正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数.
混合运算
先算乘方,再算乘除,最后算加减,如果有括号,先算括号里面的.
有理数的运算律
加法交换律
a
+
b
=
b
+
a
加法结合律
(a
+
b
)
+
c
=
a
+
(
b
+
c
)
乘法交换律
乘法结合律
ab
=
ba
(ab)c=a(bc)
乘法对加法的分配律
a(
b
+
c
)
=
ab
+
ac
随堂练习
1.计算:
解:
解:
解:
2.某商店去年四个季度盈亏情况如下(盈余为正):+128.5
万元、
-
140
万元、
-
95.5
万元、
+280
万元.这个商店去年总的盈亏情况如何?
128.5
+
(-140)
+
(-95.5)
+
280
=
173(万元)
答:盈余173万元.
3.小明记录了本小组同学的身高(单位:cm):
158,163,154,160,165,162
,157,160.
请你计算这个小组同学的平均身高.
158,163,154,160,165,162
,157,160.
解:以
160
cm
为标准身高,则小组同学的身高与标准身高的差分别是
-2
3
-6
0
5
2
-3
0
(-2+3-6+0+5+2-3+0)÷8+160
=
159.875(cm)
答:这组同学的平均身高是159.875
cm.
课堂小结
通过这节课的学习活动,你有什么收获?
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
