人教版数学九年级下册26.1.2 反比例函数的图象和性质的认识 课件( 第1课时 共24张PPT)
文档属性
| 名称 | 人教版数学九年级下册26.1.2 反比例函数的图象和性质的认识 课件( 第1课时 共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 597.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 00:00:00 | ||
图片预览





文档简介
北京和上海相距1318公里,“复兴号”高铁以v km/h的速度行驶,可在 小时后到达
1. 我们学习一次函数和二次函数时,研究了函数的哪些内容?是如何进行研究的?
我们研究了函数的解析式、图象、性质,根据解析式,通过列表、描点、连线画出函数图象,从图象的形状、位置、增减性等多个方面分析归纳函数的性质.
2.画函数图象的一般方法和步骤是怎样的?
列表、描点、连线
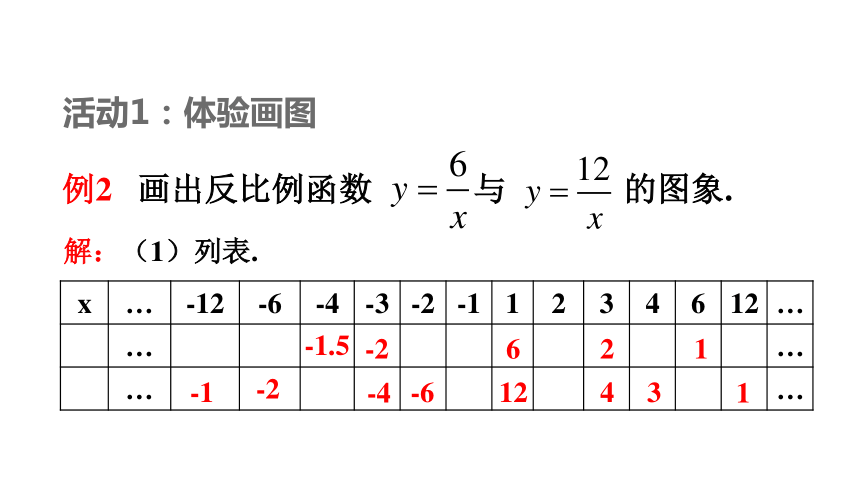
例2 画出反比例函数 与 的图象.
活动1:体验画图
解:(1)列表.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
…
…
…
…
…
-1.5
-2
6
2
1
-1
-2
-4
-6
12
4
3
1
图1
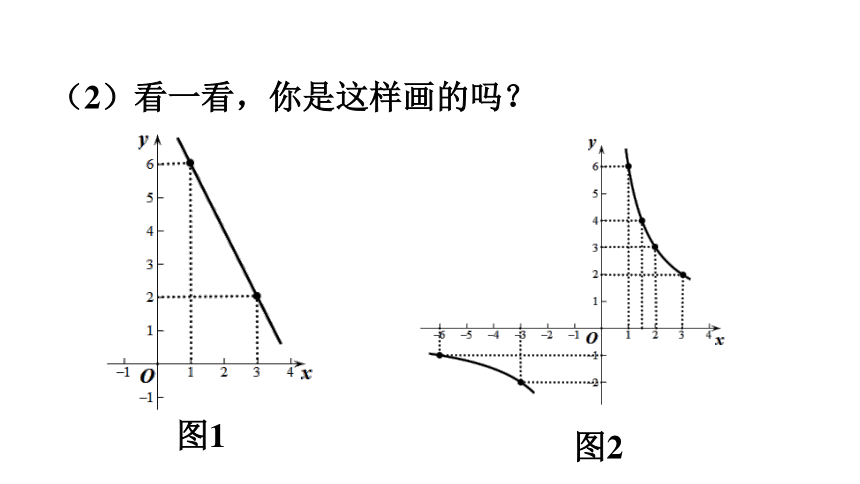
(2)看一看,你是这样画的吗?
图2
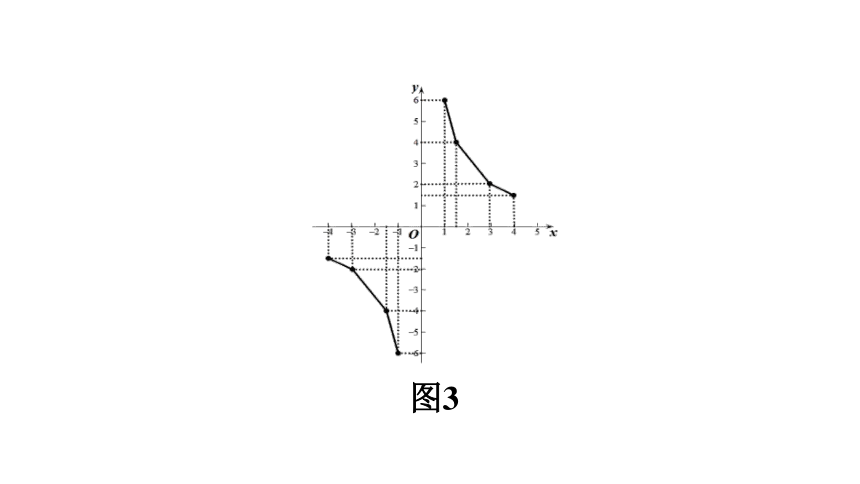
图3
①“列表”时,选取的值太少,或只取正值,不易观察出函数图象的特点,如图1;或者选取的值不关于“O”对称,如图2;
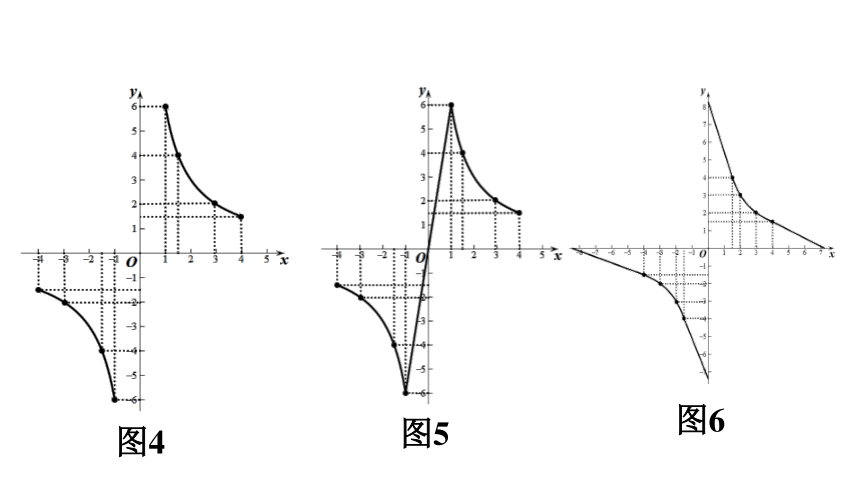
图4
图5
图6
③“连线”时,忽略自变量的取值范围是 的一切实数,如图4、图5、图6;
图7
④“连线”时,不明确图象的变化趋势,如图7.
(3)想一想:画反比例函数的图象需要注意哪些问题?
1)“列表”时,取值要有正值、负值,取值不能太少,并且需要注意取值的对称性和自变量的取值范围是 的一切实数.
2) “连线”时,注意用平滑的曲线将所描的点从左到右依次连接起来,但不与 y 轴相交.
(4)反比例函数 与 的图象.
图9
图8
(5)观察图8、图9,思考下列问题:
①每个函数图象的形状、位置、变化趋势、增减性有什么特点?
图9
图8
都是位于第一、三象限的双曲线,在每一个象限内, y 随 x 的增大而减小.
②对于反比例函数 ,①中的结论还成立吗?
只要 k 取大于 0 的数时①中的结论都成立.
③你能用函数的解析式说明②中的结论吗?
结论1:一般地,当 时,反比例函数 的图象是双曲线,双曲线的两支分别位于第一、第三象限,在每一个象限内, 随 的增大而减小.
活动2:类比探究
回顾以上研究过程,你能用类似的方法研究函数
的图象和性质吗?
结论2:一般地,当 时,反比例函数 的图象是双曲线,双曲线的两支分别位于第二、第四象限,在每一个象限内,
随 的增大而增大.
活动3:归纳性质
你能归纳出反比例函数 的性质吗?
一般地,反比例函数 的图象是双曲线,它具有以下性质:
当 时,双曲线的两支分别位于第一、第三象限,在
每一个象限内, 随 的增大而减小;
当 时,双曲线的两支分别位于第二、第四象限,在
每一个象限内, 随 的增大而增大.
D
B
C
A
C
1.(1)下列图象中是反比例图象的是( ).
(2)如图所示的图象对应的函数解析式为( ).
A.
B.
C.
D.
C
2.填空:
(1)反比例函数 的图象在第________象限.
一、三
(2)反比例函数 的图象如图所示,则k___0;在图象的每一支上,y随x的增大而______.
增大
<
3. 请每位同学构造一个你喜欢的反比例函数,同桌画出该函数图象示意图,并指出图象的形状、位置、变化趋势、增减性等.
谢 谢 观 看!
1. 我们学习一次函数和二次函数时,研究了函数的哪些内容?是如何进行研究的?
我们研究了函数的解析式、图象、性质,根据解析式,通过列表、描点、连线画出函数图象,从图象的形状、位置、增减性等多个方面分析归纳函数的性质.
2.画函数图象的一般方法和步骤是怎样的?
列表、描点、连线
例2 画出反比例函数 与 的图象.
活动1:体验画图
解:(1)列表.
{5940675A-B579-460E-94D1-54222C63F5DA}x
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
…
…
…
…
…
-1.5
-2
6
2
1
-1
-2
-4
-6
12
4
3
1
图1
(2)看一看,你是这样画的吗?
图2
图3
①“列表”时,选取的值太少,或只取正值,不易观察出函数图象的特点,如图1;或者选取的值不关于“O”对称,如图2;
图4
图5
图6
③“连线”时,忽略自变量的取值范围是 的一切实数,如图4、图5、图6;
图7
④“连线”时,不明确图象的变化趋势,如图7.
(3)想一想:画反比例函数的图象需要注意哪些问题?
1)“列表”时,取值要有正值、负值,取值不能太少,并且需要注意取值的对称性和自变量的取值范围是 的一切实数.
2) “连线”时,注意用平滑的曲线将所描的点从左到右依次连接起来,但不与 y 轴相交.
(4)反比例函数 与 的图象.
图9
图8
(5)观察图8、图9,思考下列问题:
①每个函数图象的形状、位置、变化趋势、增减性有什么特点?
图9
图8
都是位于第一、三象限的双曲线,在每一个象限内, y 随 x 的增大而减小.
②对于反比例函数 ,①中的结论还成立吗?
只要 k 取大于 0 的数时①中的结论都成立.
③你能用函数的解析式说明②中的结论吗?
结论1:一般地,当 时,反比例函数 的图象是双曲线,双曲线的两支分别位于第一、第三象限,在每一个象限内, 随 的增大而减小.
活动2:类比探究
回顾以上研究过程,你能用类似的方法研究函数
的图象和性质吗?
结论2:一般地,当 时,反比例函数 的图象是双曲线,双曲线的两支分别位于第二、第四象限,在每一个象限内,
随 的增大而增大.
活动3:归纳性质
你能归纳出反比例函数 的性质吗?
一般地,反比例函数 的图象是双曲线,它具有以下性质:
当 时,双曲线的两支分别位于第一、第三象限,在
每一个象限内, 随 的增大而减小;
当 时,双曲线的两支分别位于第二、第四象限,在
每一个象限内, 随 的增大而增大.
D
B
C
A
C
1.(1)下列图象中是反比例图象的是( ).
(2)如图所示的图象对应的函数解析式为( ).
A.
B.
C.
D.
C
2.填空:
(1)反比例函数 的图象在第________象限.
一、三
(2)反比例函数 的图象如图所示,则k___0;在图象的每一支上,y随x的增大而______.
增大
<
3. 请每位同学构造一个你喜欢的反比例函数,同桌画出该函数图象示意图,并指出图象的形状、位置、变化趋势、增减性等.
谢 谢 观 看!
