北师大版数学八年级上册 1.1 验证勾股定理及其简单计算教案(第2课时)
文档属性
| 名称 | 北师大版数学八年级上册 1.1 验证勾股定理及其简单计算教案(第2课时) |  | |
| 格式 | docx | ||
| 文件大小 | 213.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 10:17:40 | ||
图片预览




文档简介
第2课时 验证勾股定理及其简单计算
课题
第2课时 验证勾股定理及其简单计算
授课人
教
学
目
标
知识技能
掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.
数学思考
在上节课对具体的直角三角形探索发现了勾股定理的基础上,经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
问题解决
通过应用勾股定理解决实际问题,培养应用数学的意识.
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题.
教学难点
通过拼图验证勾股定理,并体会其中数形结合的思想.
授课类型
新授课
课时
教具
多媒体课件、四个全等的直角三角形图片
教学活动
教学步骤
师生活动
设计意图
回顾
1.什么是勾股定理?
2.通过怎样的方式得到勾股定理?
学生回忆并回答,为本节课的学习提供迁移或类比方法.
活动
一:
创设
情境
导入
新课
【课堂引入】
伽菲尔德是美国的第二十任总统,同时他也是一名卓越的数学家,1876年4月1日,他在《新英格兰教育日志》上发表了对勾股定理的证明,他的方法直观、简捷、易懂,人们为了纪念他就把这一证法称为“总统”证法.
问题:伽菲尔德是利用图1-1-21验证勾股定理的,你能利用它验证勾股定理吗?
图1-1-21
上节课仅仅是通过测量和数格子的方法,对具体的直角三角形进行了探索,发现了勾股定理,对一般的直角三角形仍需进行验证.巧妙引用“总统”证法引出如何验证勾股定理,引领学生不断探索,不断深入.
活动
二:
实践
探究
交流
新知
【探究1】 拼图验证勾股定理
图1-1-22是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形,对勾股定理进行验证.
图1-1-22
图1-1-23
图1-1-24
问题1:图1-1-23中正方形ABCD的边长是 ,正方形ABCD的面积可表示为 .?
问题2:图1-1-23中正方形ABCD由四个全等的直角三角形和一个小正方形组成,因此正方形ABCD的面积还可以表示为 .?
问题3:观察两种表示方法,它们表示的是同一个图形的面积,所以结果应 .?
问题4:现在,你能验证勾股定理吗?
问题5:利用图1-1-24如何验证勾股定理?
【探究2】 拓宽视野,深入了解勾股定理的证法
用图验证勾股定理的方法,据记载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的.事实上,勾股定理的证明方法十分丰富,几千年来,人们已经发现了400多种,其中有一类方法尤为独特,单靠移动几个图形就能直观地证出勾股定理,被誉为“无字的证明”,我们来欣赏几种!(课件出示)
问题:你能利用前美国总统伽菲尔德所拼的图形(如图1-1-25)验证勾股定理吗?
图1-1-25
【探究3】 探究只有直角三角形才满足a2+b2=c2
我们已经验证了直角三角形三边满足的关系,那么锐角三角形和钝角三角形的三边也满足这个关系吗?观察图1-1-26,判断图中三角形的三边长是否满足a2+b2=c2.
图1-1-26
问题1:利用数格子的方法计算图中正方形的面积分别是多少.
问题2:比较正方形的面积,锐角三角形的三边长满足的关系是什么?钝角三角形的三边长满足的关系是什么?
【总结归纳】 验证勾股定理的思路方法:
1.以直角三角形的三边为探究目标;
2.通过利用直角三角形的三边构造相应的全等图形(可以通过翻折、拼凑、割补等方式);
3.将“零散”的图形整体化,利用“部分图形”的面积之和等于“整体图形”的面积来验证勾股定理.
1.让学生体会数形结合的思想,通过探究图形的构成,亲身验证勾股定理的正确性,学生的动手、动脑能力得到了加强.图1-1-23、图1-1-24都能够证明勾股定理,并且这两个图形的证明方法类似,因此师生共同来完成一个即可,剩下的一个由学生独立证明,目的是学以致用,以实践操作强化对知识的理解.
2.介绍中外古代人们对勾股定理证明的研究,特别是勾股定理的“无字证明”,从另一个角度让学生感受勾股定理的证明思路,体会拼图方法的多样性,激发学生的学习兴趣.让学生验证“总统”证法的正确性,希望学生能关注知识、方法之间的内在联系,通过学生自身的实践活动加深对勾股定理的理解.
3.学生通过数格子的方法可以得出“如果一个三角形不是直角三角形,那么它的三边a,b,c不满足a2+b2=c2”这个结论,这样可以使学生加深对勾股定理的认识,也为下一节学习直角三角形的判别打下基础.
活动
三:
开放
训练
体现
应用
【应用举例】
例 (教材例题)我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗?
变式训练
1.一个寻宝探险小队,从点A出发探寻宝藏,他们向东行走4千米到达点C,然后又向正北行走2.5千米到达点D,接着他们又向正东继续行走2千米到达点E,最后他们又向正北前进了5.5千米到达点B才找到了宝藏,你能准确地求出宝藏藏匿点B距离出发点A多少千米吗?
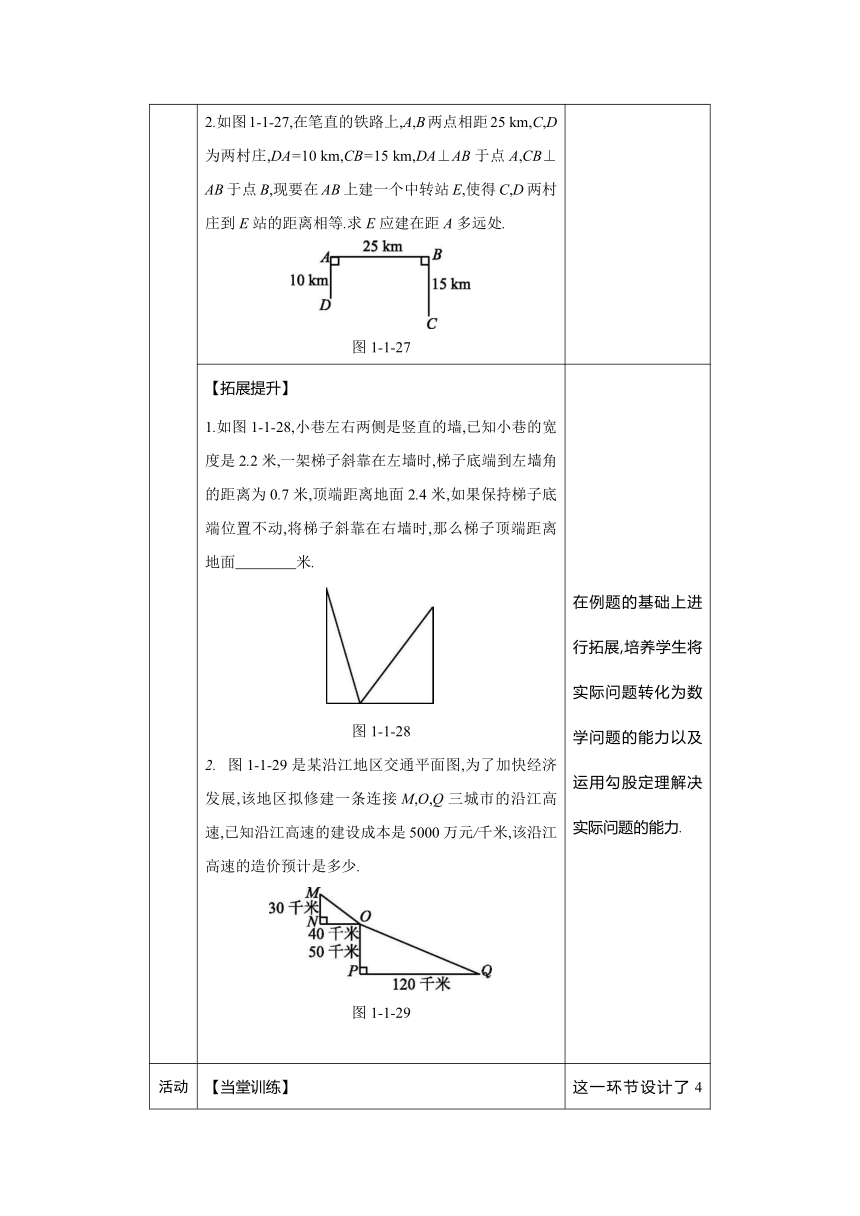
2.如图1-1-27,在笔直的铁路上,A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个中转站E,使得C,D两村庄到E站的距离相等.求E应建在距A多远处.
图1-1-27
为了巩固所学的勾股定理知识,教师可逐步引导学生初步运用勾股定理解决实际问题,强化应用的意识,在应用中体会勾股定理的价值.
【拓展提升】
1.如图1-1-28,小巷左右两侧是竖直的墙,已知小巷的宽度是2.2米,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,那么梯子顶端距离地面 米.?
图1-1-28
图1-1-29是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是5000万元/千米,该沿江高速的造价预计是多少.
图1-1-29
在例题的基础上进行拓展,培养学生将实际问题转化为数学问题的能力以及运用勾股定理解决实际问题的能力.
活动
四:
课堂
总结
反思
【当堂训练】
1.放学以后,小红和小颖从学校分别,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A.600米 B.800米
C.1000米 D.不能确定
2.如图1-1-30,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形DCEF的面积.
图1-1-30
3.如图1-1-31,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动 米.?
图1-1-31
4.如图1-1-32,受台风“山竹”的影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
图1-1-32
这一环节设计了4道题,设计时注意了题目的难易梯度,由浅入深,第1,2题学生容易解决,第3,4题虽然计算难度不大,但考查学生的实际应用能力,有一定难度.在例题的基础上进行拓展,训练学生将实际问题转化为数学问题,再运用勾股定理解决问题的能力.
【课堂总结】
学生活动:谈谈本节课的收获与体会.
教学说明:学生先独立完成小结,在学生回答的过程中,老师引导学生将本节课的知识系统化.
作业:课本P6习题1.2中的T1、T3.
【板书设计】
第2课时 验证勾股定理及其简单计算
一、拼图验证勾股定理 二、例 三、练习
1.(a+b)2=12ab×4+c2,即a2+b2=c2.
2.c2=12ab×4+(b-a)2,即a2+b2=c2.
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
巧妙引用“总统”证法引出如何验证勾股定理,激起学生的好奇心,点燃学生的求知欲,以景激情,以情促思,引领学生不断探索,不断深入.
②[讲授效果反思]
勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,我设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法1,最后由学生独立探究得到方法2,这样使学生较容易地突破了本节课的难点.
③[师生互动反思]
④[习题反思]
好题题号 ?
错题题号 ?
反思,更进一步提升.
典案二 导学设计
一、学习目标
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
3、进一步体会数形结合的思想以及数学知识之间内在联系。
二、学习方法
自主探究与合作交流相结合
三、学习重难点:
能熟练应用拼图法(用面积)证明勾股定理.
四、学习过程
模块一 预习反馈
1、查阅资料,网络搜索有关勾股定理的知识。
2、画四个全等的直角三角形,并把它剪下来,用这四个直角三角形拼一拼、摆一摆,选择自己最喜欢的拼图方法,验证勾股定理。
3、你还知道其它验证勾股定理的方法吗?
归纳梳理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么?
4、在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=________;
(2)b=8,c=17,则S△ABC=________。
(提示先构好图)
5524504406904、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
模块二 合作探究
1、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米?
36576001981202、如下图所示,某人在B处通过平面镜看见在B正上方5米处的A物体,已知物体A到平面镜的距离为6米,问B点到物体A的像A′的距离是多少?
3、在平静的湖面上,有一棵水草,它高出水面3分米,一阵风吹来;水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6分米,问这里的水深是多少?
35433002971804、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
模块三 形成提升
1、如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于多少?
A
B
C
P
P′
false2.如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
3、如图,在△ABC中,D是BC上一点,且满足AC=AD,A
B
C
D
请你说明AB2=AC2+BC·BD.
模块四 小结评价
这一节课我们一起学习了哪些知识和思想方法?
知识:
方法:
本节易错点:
课外作业:
A层:
填空题
1.假如有一个三角形是直角三角形,那么三边、、之间应满足 ,其中 边是直角所对的边;如果一个三角形的三边、、满足,那么这个三角形是 三角形,其中边是 边,边所对的角是
2、已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=6,c=10,则b=_______;
④若c=25,b=15,则a=________
3、直角三角形的周长是24cm,斜边上的中线长为5cm,则此三角形的面积是 。
4、在直角三角形中,如果两直角边之和为17,两直角边之平方差为119,则斜边的长为
.
5.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
6.如图1,已知中,,,,以直角边为直径作半圆,则这个半圆的面积是 .
图1
A
C
B
7.如图2,一个高、宽的大门,需要在对角线的顶点间加固一个木条,求木条的长.
图2
B层:
1.如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
3m
4m
20m
A
小汽车
小汽车
B
C
观测点
2.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为m,这辆小汽车超速了吗?
3.如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
365760071120
29654502152654、如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交于AC于M,若CM=5,求CE2 +CF2的值。
课题
第2课时 验证勾股定理及其简单计算
授课人
教
学
目
标
知识技能
掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.
数学思考
在上节课对具体的直角三角形探索发现了勾股定理的基础上,经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
问题解决
通过应用勾股定理解决实际问题,培养应用数学的意识.
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题.
教学难点
通过拼图验证勾股定理,并体会其中数形结合的思想.
授课类型
新授课
课时
教具
多媒体课件、四个全等的直角三角形图片
教学活动
教学步骤
师生活动
设计意图
回顾
1.什么是勾股定理?
2.通过怎样的方式得到勾股定理?
学生回忆并回答,为本节课的学习提供迁移或类比方法.
活动
一:
创设
情境
导入
新课
【课堂引入】
伽菲尔德是美国的第二十任总统,同时他也是一名卓越的数学家,1876年4月1日,他在《新英格兰教育日志》上发表了对勾股定理的证明,他的方法直观、简捷、易懂,人们为了纪念他就把这一证法称为“总统”证法.
问题:伽菲尔德是利用图1-1-21验证勾股定理的,你能利用它验证勾股定理吗?
图1-1-21
上节课仅仅是通过测量和数格子的方法,对具体的直角三角形进行了探索,发现了勾股定理,对一般的直角三角形仍需进行验证.巧妙引用“总统”证法引出如何验证勾股定理,引领学生不断探索,不断深入.
活动
二:
实践
探究
交流
新知
【探究1】 拼图验证勾股定理
图1-1-22是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形,对勾股定理进行验证.
图1-1-22
图1-1-23
图1-1-24
问题1:图1-1-23中正方形ABCD的边长是 ,正方形ABCD的面积可表示为 .?
问题2:图1-1-23中正方形ABCD由四个全等的直角三角形和一个小正方形组成,因此正方形ABCD的面积还可以表示为 .?
问题3:观察两种表示方法,它们表示的是同一个图形的面积,所以结果应 .?
问题4:现在,你能验证勾股定理吗?
问题5:利用图1-1-24如何验证勾股定理?
【探究2】 拓宽视野,深入了解勾股定理的证法
用图验证勾股定理的方法,据记载最早是三国时期数学家赵爽在为《周髀算经》作注时给出的.事实上,勾股定理的证明方法十分丰富,几千年来,人们已经发现了400多种,其中有一类方法尤为独特,单靠移动几个图形就能直观地证出勾股定理,被誉为“无字的证明”,我们来欣赏几种!(课件出示)
问题:你能利用前美国总统伽菲尔德所拼的图形(如图1-1-25)验证勾股定理吗?
图1-1-25
【探究3】 探究只有直角三角形才满足a2+b2=c2
我们已经验证了直角三角形三边满足的关系,那么锐角三角形和钝角三角形的三边也满足这个关系吗?观察图1-1-26,判断图中三角形的三边长是否满足a2+b2=c2.
图1-1-26
问题1:利用数格子的方法计算图中正方形的面积分别是多少.
问题2:比较正方形的面积,锐角三角形的三边长满足的关系是什么?钝角三角形的三边长满足的关系是什么?
【总结归纳】 验证勾股定理的思路方法:
1.以直角三角形的三边为探究目标;
2.通过利用直角三角形的三边构造相应的全等图形(可以通过翻折、拼凑、割补等方式);
3.将“零散”的图形整体化,利用“部分图形”的面积之和等于“整体图形”的面积来验证勾股定理.
1.让学生体会数形结合的思想,通过探究图形的构成,亲身验证勾股定理的正确性,学生的动手、动脑能力得到了加强.图1-1-23、图1-1-24都能够证明勾股定理,并且这两个图形的证明方法类似,因此师生共同来完成一个即可,剩下的一个由学生独立证明,目的是学以致用,以实践操作强化对知识的理解.
2.介绍中外古代人们对勾股定理证明的研究,特别是勾股定理的“无字证明”,从另一个角度让学生感受勾股定理的证明思路,体会拼图方法的多样性,激发学生的学习兴趣.让学生验证“总统”证法的正确性,希望学生能关注知识、方法之间的内在联系,通过学生自身的实践活动加深对勾股定理的理解.
3.学生通过数格子的方法可以得出“如果一个三角形不是直角三角形,那么它的三边a,b,c不满足a2+b2=c2”这个结论,这样可以使学生加深对勾股定理的认识,也为下一节学习直角三角形的判别打下基础.
活动
三:
开放
训练
体现
应用
【应用举例】
例 (教材例题)我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗?
变式训练
1.一个寻宝探险小队,从点A出发探寻宝藏,他们向东行走4千米到达点C,然后又向正北行走2.5千米到达点D,接着他们又向正东继续行走2千米到达点E,最后他们又向正北前进了5.5千米到达点B才找到了宝藏,你能准确地求出宝藏藏匿点B距离出发点A多少千米吗?
2.如图1-1-27,在笔直的铁路上,A,B两点相距25 km,C,D为两村庄,DA=10 km,CB=15 km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个中转站E,使得C,D两村庄到E站的距离相等.求E应建在距A多远处.
图1-1-27
为了巩固所学的勾股定理知识,教师可逐步引导学生初步运用勾股定理解决实际问题,强化应用的意识,在应用中体会勾股定理的价值.
【拓展提升】
1.如图1-1-28,小巷左右两侧是竖直的墙,已知小巷的宽度是2.2米,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,那么梯子顶端距离地面 米.?
图1-1-28
图1-1-29是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是5000万元/千米,该沿江高速的造价预计是多少.
图1-1-29
在例题的基础上进行拓展,培养学生将实际问题转化为数学问题的能力以及运用勾股定理解决实际问题的能力.
活动
四:
课堂
总结
反思
【当堂训练】
1.放学以后,小红和小颖从学校分别,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A.600米 B.800米
C.1000米 D.不能确定
2.如图1-1-30,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形DCEF的面积.
图1-1-30
3.如图1-1-31,一架云梯长10米,斜靠在一面墙上,梯子顶端离地面6米,要使梯子顶端离地面8米,则梯子的底部在水平面方向要向左滑动 米.?
图1-1-31
4.如图1-1-32,受台风“山竹”的影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
图1-1-32
这一环节设计了4道题,设计时注意了题目的难易梯度,由浅入深,第1,2题学生容易解决,第3,4题虽然计算难度不大,但考查学生的实际应用能力,有一定难度.在例题的基础上进行拓展,训练学生将实际问题转化为数学问题,再运用勾股定理解决问题的能力.
【课堂总结】
学生活动:谈谈本节课的收获与体会.
教学说明:学生先独立完成小结,在学生回答的过程中,老师引导学生将本节课的知识系统化.
作业:课本P6习题1.2中的T1、T3.
【板书设计】
第2课时 验证勾股定理及其简单计算
一、拼图验证勾股定理 二、例 三、练习
1.(a+b)2=12ab×4+c2,即a2+b2=c2.
2.c2=12ab×4+(b-a)2,即a2+b2=c2.
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
巧妙引用“总统”证法引出如何验证勾股定理,激起学生的好奇心,点燃学生的求知欲,以景激情,以情促思,引领学生不断探索,不断深入.
②[讲授效果反思]
勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,我设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法1,最后由学生独立探究得到方法2,这样使学生较容易地突破了本节课的难点.
③[师生互动反思]
④[习题反思]
好题题号 ?
错题题号 ?
反思,更进一步提升.
典案二 导学设计
一、学习目标
1、了解多种拼图方法,验证勾股定理,感受解决同一个问题方法的多样性。
2、通过实例进一步了解勾股定理,应用勾股定理进行简单的计算和证明。,
3、进一步体会数形结合的思想以及数学知识之间内在联系。
二、学习方法
自主探究与合作交流相结合
三、学习重难点:
能熟练应用拼图法(用面积)证明勾股定理.
四、学习过程
模块一 预习反馈
1、查阅资料,网络搜索有关勾股定理的知识。
2、画四个全等的直角三角形,并把它剪下来,用这四个直角三角形拼一拼、摆一摆,选择自己最喜欢的拼图方法,验证勾股定理。
3、你还知道其它验证勾股定理的方法吗?
归纳梳理:
① 用语言表达勾股定理
② 用式子表达勾股定理
③ 运用勾股定理时该注意些什么?
4、在Rt△ABC中,∠C=90°
(1)若a=5,b=12,则c=________;
(2)b=8,c=17,则S△ABC=________。
(提示先构好图)
5524504406904、下列各图中所示的线段的长度或正方形的面积为多少。(注:下列各图中的三角形均为直角三角形)
模块二 合作探究
1、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000 米处,过了 20 秒,飞机距离这个男孩头顶5000米,飞机每时飞行多少千米?
36576001981202、如下图所示,某人在B处通过平面镜看见在B正上方5米处的A物体,已知物体A到平面镜的距离为6米,问B点到物体A的像A′的距离是多少?
3、在平静的湖面上,有一棵水草,它高出水面3分米,一阵风吹来;水草被吹到一边,草尖齐至水面,已知水草移动的水平距离为6分米,问这里的水深是多少?
35433002971804、如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
提示:
① AD 与BD有何关系?
② 设CD=x,则AD=
③ 在△ACD中根据勾股定理可列出
构造方程来解。
模块三 形成提升
1、如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于多少?
A
B
C
P
P′
false2.如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
3、如图,在△ABC中,D是BC上一点,且满足AC=AD,A
B
C
D
请你说明AB2=AC2+BC·BD.
模块四 小结评价
这一节课我们一起学习了哪些知识和思想方法?
知识:
方法:
本节易错点:
课外作业:
A层:
填空题
1.假如有一个三角形是直角三角形,那么三边、、之间应满足 ,其中 边是直角所对的边;如果一个三角形的三边、、满足,那么这个三角形是 三角形,其中边是 边,边所对的角是
2、已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=6,c=10,则b=_______;
④若c=25,b=15,则a=________
3、直角三角形的周长是24cm,斜边上的中线长为5cm,则此三角形的面积是 。
4、在直角三角形中,如果两直角边之和为17,两直角边之平方差为119,则斜边的长为
.
5.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。
6.如图1,已知中,,,,以直角边为直径作半圆,则这个半圆的面积是 .
图1
A
C
B
7.如图2,一个高、宽的大门,需要在对角线的顶点间加固一个木条,求木条的长.
图2
B层:
1.如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
3m
4m
20m
A
小汽车
小汽车
B
C
观测点
2.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过km/h.如图,,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为m,这辆小汽车超速了吗?
3.如图,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
365760071120
29654502152654、如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交于AC于M,若CM=5,求CE2 +CF2的值。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
