北师大版数学七年级上册第一章 丰富的图形世界 单元测试题(word版,含答案)
文档属性
| 名称 | 北师大版数学七年级上册第一章 丰富的图形世界 单元测试题(word版,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-15 00:00:00 | ||
图片预览


文档简介
北师大版七年级数学上册第一章丰富的图形世界单元测试题
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
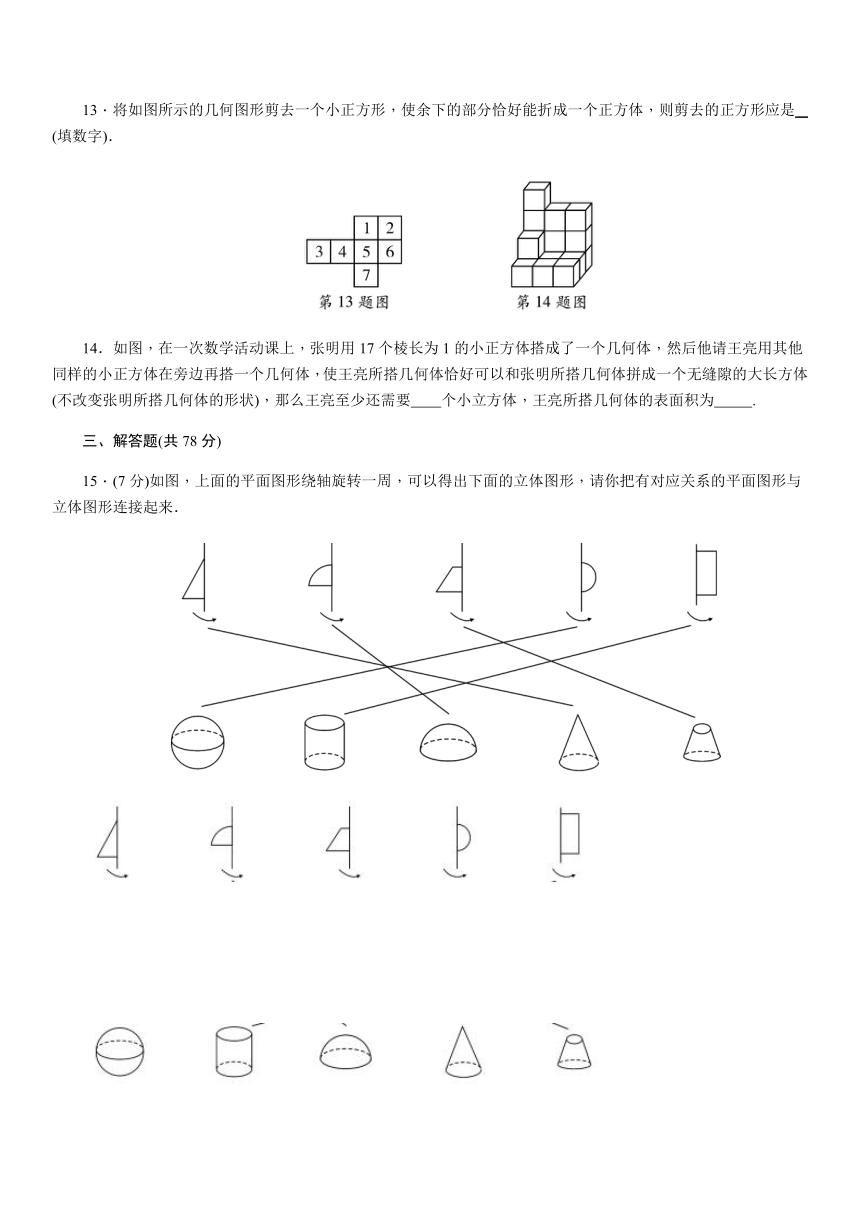
1.如图所示,物体的形状是(
)
A.棱柱
B.圆柱
C.圆锥
D.球
第1题图
第2题图
第6题图
2.如图所示物体从正面看得到的形状图是(
)
3.下列四个图形中是正方体的平面展开图的是(
)
4.将如图所示的直角三角形ABC绕直角边AB旋转一周,所得几何体从左面看为(
)
5.圆柱和圆锥的共同点是(
)
A.都有顶点
B.底面是平面,侧面是曲面
C.面数相同
D.都没有顶点
6.如图是由六个棱长为1的立方块组成的一个几何体,从上面看得到的图形的面积是(
)
A.6
B.5
C.4
D.3
7.如图是一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是(
)
8.如图,有一个正方体纸巾盒,它的平面展开图是(
)
9.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形,则该圆柱的底面圆半径是(
)
A.
B.
C.或
D.或
10.图①是一个小正方体的表面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是(
)
A.梦
B.水
C.城
D.美
第10题图
第12题图
二、填空题(每小题3分,共12分)
11.用一个平面去截几何体,若截面是三角形,则这个几何体可能是
(只填一个即可).
12.一个几何体的从三个不同的方向看得到的形状图如图所示,则该几何体是
.
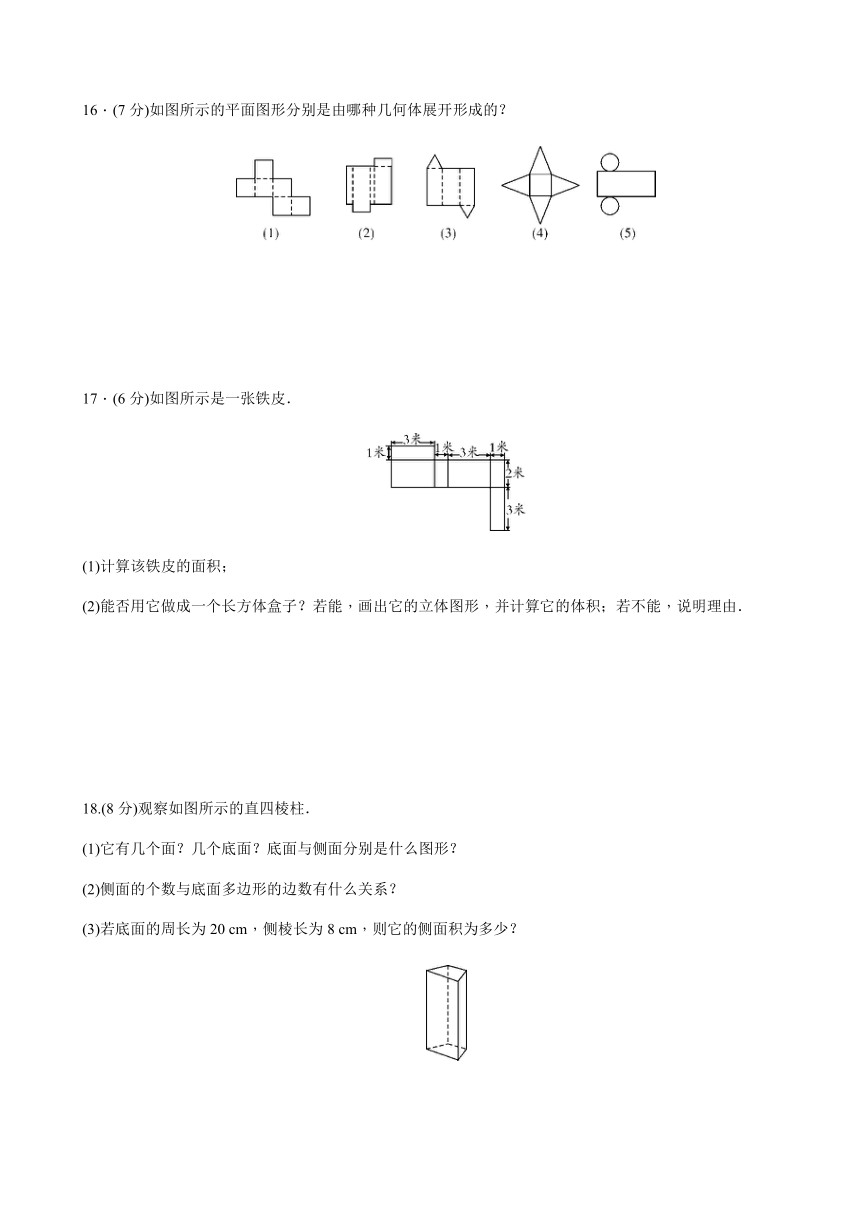
13.将如图所示的几何图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则剪去的正方形应是
(填数字).
14.如图,在一次数学活动课上,张明用17个棱长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
个小立方体,王亮所搭几何体的表面积为
.
三、解答题(共78分)
15.(7分)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
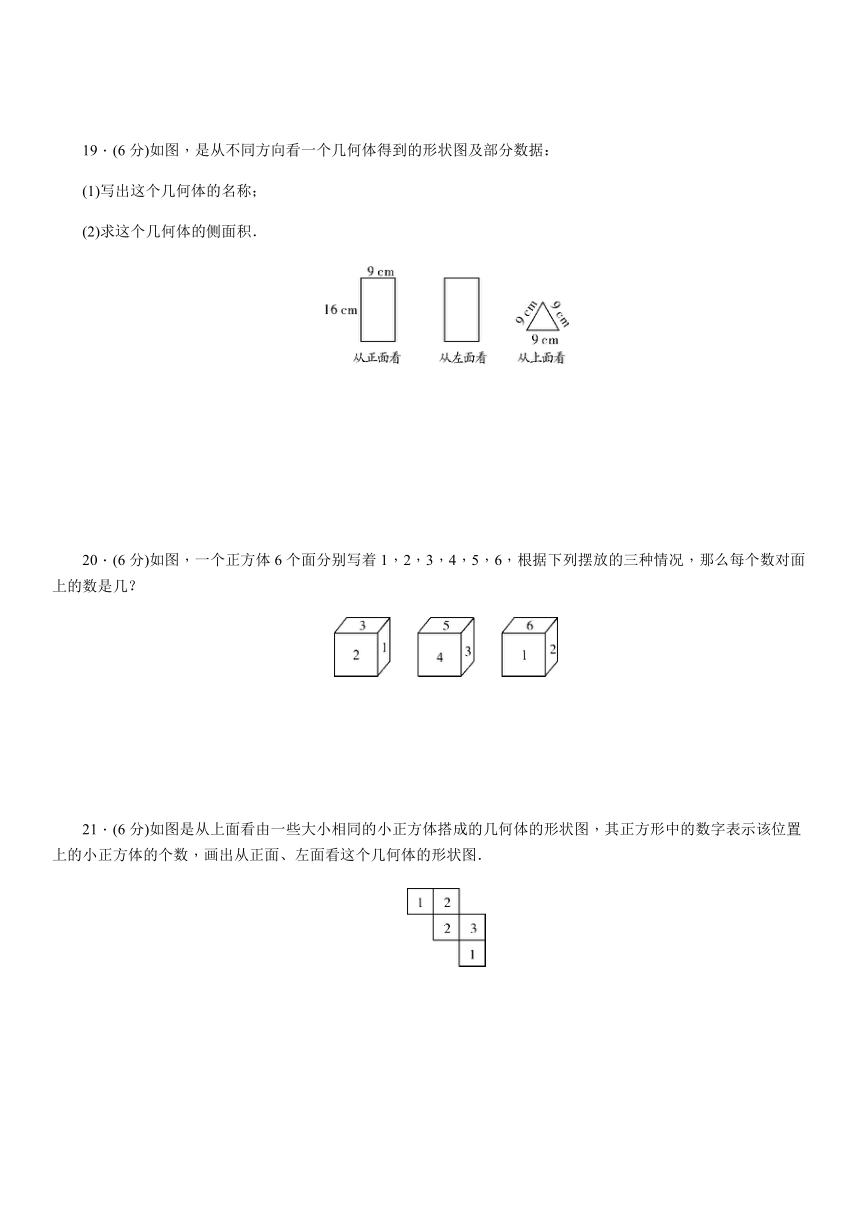
16.(7分)如图所示的平面图形分别是由哪种几何体展开形成的?
17.(6分)如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)能否用它做成一个长方体盒子?若能,画出它的立体图形,并计算它的体积;若不能,说明理由.
18.(8分)观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
19.(6分)如图,是从不同方向看一个几何体得到的形状图及部分数据:
(1)写出这个几何体的名称;
(2)求这个几何体的侧面积.
20.(6分)如图,一个正方体6个面分别写着1,2,3,4,5,6,根据下列摆放的三种情况,那么每个数对面上的数是几?
21.(6分)如图是从上面看由一些大小相同的小正方体搭成的几何体的形状图,其正方形中的数字表示该位置上的小正方体的个数,画出从正面、左面看这个几何体的形状图.
22.(8分)已知有一个长为5
cm,宽为3
cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?
23.(8分)一个几何体是由一些大小相同的小正方体摆成的,从正面与左面看到的图形如图所示,则组成这个几何体的小正方体最少有多少个?最多有多少个?
24.(8分)丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.观察:下面这些几何体都是简单几何体,请你仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体
a
b
c
d
e
棱数(E)
6
9
15
面数(F)
4
5
5
6
____
顶点数(V)
4
5
8
发现:(1)简单几何体中,V+F-E=____.
(2)简单几何体中,每条棱都是
个面的公共边;
(3)在正方体中,每个顶点处有
条棱,每条棱都有
个顶点,所以有2×E=3×V.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有
条棱,
个顶点,每个顶点处有
条棱.
(8分)如图,左图为一个棱长为4的正方体,右图为左图的表面展开图(字在外表面上),请根据要求回答问题:
(1)面“成”的对面是面
;
(2)如果面“丽”在右面,面“美”在后面,面
会在上面;
(3)左图中,M,N为所在棱的中点,试在右图中画出点M,N的位置;右图中三角形AMN的面积为
.
参考答案
一、选择题(每小题3分,共30分)
1.如图所示,物体的形状是( A )
A.棱柱
B.圆柱
C.圆锥
D.球
第1题图
第2题图
第6题图
2.(
3.下列四个图形中是正方体的平面展开图的是( B )
4.将如图所示的直角三角形ABC绕直角边AB旋转一周,所得几何体从左面看为( C )
5.圆柱和圆锥的共同点是( B )
A.都有顶点
B.底面是平面,侧面是曲面
C.面数相同
D.都没有顶点
6.如图是由六个棱长为1的立方块组成的一个几何体,从上面看得到的图形的面积是( B )
A.6
B.5
C.4
D.3
7.如图是一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( B )
8.如图,有一个正方体纸巾盒,它的平面展开图是( B )
9.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形,则该圆柱的底面圆半径是( C )
A.
B.
C.或
D.或
10.图①是一个小正方体的表面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( A )
A.梦
B.水
C.城
D.美
第10题图
第12题图
二、填空题(每小题3分,共12分)
11.用一个平面去截几何体,若截面是三角形,则这个几何体可能是
正方体
(只填一个即可).
12.一个几何体的从三个不同的方向看得到的形状图如图所示,则该几何体是
三棱柱.
13.将如图所示的几何图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则剪去的正方形应是
1或2
(填数字).
14.如图,在一次数学活动课上,张明用17个棱长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
19
个小立方体,王亮所搭几何体的表面积为
48
.
三、解答题(共78分)
15.(7分)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
16.(7分)如图所示的平面图形分别是由哪种几何体展开形成的?
解:(1)正方体;(2)四棱柱;(3)三棱柱;(4)四棱锥;(5)圆柱.
17.(6分)如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)能否用它做成一个长方体盒子?若能,画出它的立体图形,并计算它的体积;若不能,说明理由.
解:(1)(1+2)×3+(1+3+1)×2+3×1=22
m2;
(2)能, 体积为3×2×1=6
m3.
18.(8分)观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;
(2)侧面的个数与底面多边形的边数相等,都为4;
(3)它的侧面积为20×
8=160
cm2.
19.(6分)如图,是从不同方向看一个几何体得到的形状图及部分数据:
(1)写出这个几何体的名称;
(2)求这个几何体的侧面积.
解:(1)三棱柱;(2)这个几何体的侧面积为3×16×9=432
cm2.
20.(6分)如图,一个正方体6个面分别写着1,2,3,4,5,6,根据下列摆放的三种情况,那么每个数对面上的数是几?
解:根据正方体的特征知,相邻的面一定不是对面,所以面“1”与面“4”相对,面“2”与面“5”相对,面“3”与面“6”相对.1对4,2对5,3对6.
21.(6分)如图是从上面看由一些大小相同的小正方体搭成的几何体的形状图,其正方形中的数字表示该位置上的小正方体的个数,画出从正面、左面看这个几何体的形状图.
解:
22.(8分)已知有一个长为5
cm,宽为3
cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?
解:①以长为5
cm的边所在直线为轴,旋转一周时,所得图形的表面积为2×32×π+5×2×3π=48π
cm2;②以长为3
cm的边所在直线为轴,旋转一周时,所得图形的表面积为2×52×π+3×2×5π=80π
cm2.故所得几何体的表面积为48π
cm2或80π
cm2.
23.(8分)一个几何体是由一些大小相同的小正方体摆成的,从正面与左面看到的图形如图所示,则组成这个几何体的小正方体最少有多少个?最多有多少个?
解:综合从正面和左面看到的图形,这个几何体的底层最少有2+1=3个小正方体,最多有2+2=4个小正方体;第二层有2个小正方体,因此组成这个几何体最少有3+2=5个小正方体,最多有4+2=6个小正方体.
24.(8分)丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.观察:下面这些几何体都是简单几何体,请你仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体
a
b
c
d
e
棱数(E)
6
8
9
12
15
面数(F)
4
5
5
6
__7__
顶点数(V)
4
5
6
8
10
发现:(1)简单几何体中,V+F-E=__2__.
(2)简单几何体中,每条棱都是
2
个面的公共边;
(3)在正方体中,每个顶点处有
3
条棱,每条棱都有
2
个顶点,所以有2×E=3×V.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有
30
条棱,
20
个顶点,每个顶点处有
3
条棱.
25.(8分)如图,左图为一个棱长为4的正方体,右图为左图的表面展开图(字在外表面上),请根据要求回答问题:
(1)面“成”的对面是面
“爱”
;
(2)如果面“丽”在右面,面“美”在后面,面
“成”
会在上面;
(3)左图中,M,N为所在棱的中点,试在右图中画出点M,N的位置;右图中三角形AMN的面积为
18或10
.
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图所示,物体的形状是(
)
A.棱柱
B.圆柱
C.圆锥
D.球
第1题图
第2题图
第6题图
2.如图所示物体从正面看得到的形状图是(
)
3.下列四个图形中是正方体的平面展开图的是(
)
4.将如图所示的直角三角形ABC绕直角边AB旋转一周,所得几何体从左面看为(
)
5.圆柱和圆锥的共同点是(
)
A.都有顶点
B.底面是平面,侧面是曲面
C.面数相同
D.都没有顶点
6.如图是由六个棱长为1的立方块组成的一个几何体,从上面看得到的图形的面积是(
)
A.6
B.5
C.4
D.3
7.如图是一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是(
)
8.如图,有一个正方体纸巾盒,它的平面展开图是(
)
9.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形,则该圆柱的底面圆半径是(
)
A.
B.
C.或
D.或
10.图①是一个小正方体的表面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是(
)
A.梦
B.水
C.城
D.美
第10题图
第12题图
二、填空题(每小题3分,共12分)
11.用一个平面去截几何体,若截面是三角形,则这个几何体可能是
(只填一个即可).
12.一个几何体的从三个不同的方向看得到的形状图如图所示,则该几何体是
.
13.将如图所示的几何图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则剪去的正方形应是
(填数字).
14.如图,在一次数学活动课上,张明用17个棱长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
个小立方体,王亮所搭几何体的表面积为
.
三、解答题(共78分)
15.(7分)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
16.(7分)如图所示的平面图形分别是由哪种几何体展开形成的?
17.(6分)如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)能否用它做成一个长方体盒子?若能,画出它的立体图形,并计算它的体积;若不能,说明理由.
18.(8分)观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
19.(6分)如图,是从不同方向看一个几何体得到的形状图及部分数据:
(1)写出这个几何体的名称;
(2)求这个几何体的侧面积.
20.(6分)如图,一个正方体6个面分别写着1,2,3,4,5,6,根据下列摆放的三种情况,那么每个数对面上的数是几?
21.(6分)如图是从上面看由一些大小相同的小正方体搭成的几何体的形状图,其正方形中的数字表示该位置上的小正方体的个数,画出从正面、左面看这个几何体的形状图.
22.(8分)已知有一个长为5
cm,宽为3
cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?
23.(8分)一个几何体是由一些大小相同的小正方体摆成的,从正面与左面看到的图形如图所示,则组成这个几何体的小正方体最少有多少个?最多有多少个?
24.(8分)丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.观察:下面这些几何体都是简单几何体,请你仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体
a
b
c
d
e
棱数(E)
6
9
15
面数(F)
4
5
5
6
____
顶点数(V)
4
5
8
发现:(1)简单几何体中,V+F-E=____.
(2)简单几何体中,每条棱都是
个面的公共边;
(3)在正方体中,每个顶点处有
条棱,每条棱都有
个顶点,所以有2×E=3×V.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有
条棱,
个顶点,每个顶点处有
条棱.
(8分)如图,左图为一个棱长为4的正方体,右图为左图的表面展开图(字在外表面上),请根据要求回答问题:
(1)面“成”的对面是面
;
(2)如果面“丽”在右面,面“美”在后面,面
会在上面;
(3)左图中,M,N为所在棱的中点,试在右图中画出点M,N的位置;右图中三角形AMN的面积为
.
参考答案
一、选择题(每小题3分,共30分)
1.如图所示,物体的形状是( A )
A.棱柱
B.圆柱
C.圆锥
D.球
第1题图
第2题图
第6题图
2.(
3.下列四个图形中是正方体的平面展开图的是( B )
4.将如图所示的直角三角形ABC绕直角边AB旋转一周,所得几何体从左面看为( C )
5.圆柱和圆锥的共同点是( B )
A.都有顶点
B.底面是平面,侧面是曲面
C.面数相同
D.都没有顶点
6.如图是由六个棱长为1的立方块组成的一个几何体,从上面看得到的图形的面积是( B )
A.6
B.5
C.4
D.3
7.如图是一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是( B )
8.如图,有一个正方体纸巾盒,它的平面展开图是( B )
9.一个圆柱的侧面展开图是两邻边长分别为6和8的矩形,则该圆柱的底面圆半径是( C )
A.
B.
C.或
D.或
10.图①是一个小正方体的表面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( A )
A.梦
B.水
C.城
D.美
第10题图
第12题图
二、填空题(每小题3分,共12分)
11.用一个平面去截几何体,若截面是三角形,则这个几何体可能是
正方体
(只填一个即可).
12.一个几何体的从三个不同的方向看得到的形状图如图所示,则该几何体是
三棱柱.
13.将如图所示的几何图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则剪去的正方形应是
1或2
(填数字).
14.如图,在一次数学活动课上,张明用17个棱长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
19
个小立方体,王亮所搭几何体的表面积为
48
.
三、解答题(共78分)
15.(7分)如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
16.(7分)如图所示的平面图形分别是由哪种几何体展开形成的?
解:(1)正方体;(2)四棱柱;(3)三棱柱;(4)四棱锥;(5)圆柱.
17.(6分)如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)能否用它做成一个长方体盒子?若能,画出它的立体图形,并计算它的体积;若不能,说明理由.
解:(1)(1+2)×3+(1+3+1)×2+3×1=22
m2;
(2)能, 体积为3×2×1=6
m3.
18.(8分)观察如图所示的直四棱柱.
(1)它有几个面?几个底面?底面与侧面分别是什么图形?
(2)侧面的个数与底面多边形的边数有什么关系?
(3)若底面的周长为20
cm,侧棱长为8
cm,则它的侧面积为多少?
解:(1)它有6个面,2个底面,底面是梯形,侧面是长方形;
(2)侧面的个数与底面多边形的边数相等,都为4;
(3)它的侧面积为20×
8=160
cm2.
19.(6分)如图,是从不同方向看一个几何体得到的形状图及部分数据:
(1)写出这个几何体的名称;
(2)求这个几何体的侧面积.
解:(1)三棱柱;(2)这个几何体的侧面积为3×16×9=432
cm2.
20.(6分)如图,一个正方体6个面分别写着1,2,3,4,5,6,根据下列摆放的三种情况,那么每个数对面上的数是几?
解:根据正方体的特征知,相邻的面一定不是对面,所以面“1”与面“4”相对,面“2”与面“5”相对,面“3”与面“6”相对.1对4,2对5,3对6.
21.(6分)如图是从上面看由一些大小相同的小正方体搭成的几何体的形状图,其正方形中的数字表示该位置上的小正方体的个数,画出从正面、左面看这个几何体的形状图.
解:
22.(8分)已知有一个长为5
cm,宽为3
cm的长方形,若以这个长方形的一边所在的直线为轴,将它旋转一周,你能求出所得的几何体的表面积吗?
解:①以长为5
cm的边所在直线为轴,旋转一周时,所得图形的表面积为2×32×π+5×2×3π=48π
cm2;②以长为3
cm的边所在直线为轴,旋转一周时,所得图形的表面积为2×52×π+3×2×5π=80π
cm2.故所得几何体的表面积为48π
cm2或80π
cm2.
23.(8分)一个几何体是由一些大小相同的小正方体摆成的,从正面与左面看到的图形如图所示,则组成这个几何体的小正方体最少有多少个?最多有多少个?
解:综合从正面和左面看到的图形,这个几何体的底层最少有2+1=3个小正方体,最多有2+2=4个小正方体;第二层有2个小正方体,因此组成这个几何体最少有3+2=5个小正方体,最多有4+2=6个小正方体.
24.(8分)丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.观察:下面这些几何体都是简单几何体,请你仔细观察.
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体
a
b
c
d
e
棱数(E)
6
8
9
12
15
面数(F)
4
5
5
6
__7__
顶点数(V)
4
5
6
8
10
发现:(1)简单几何体中,V+F-E=__2__.
(2)简单几何体中,每条棱都是
2
个面的公共边;
(3)在正方体中,每个顶点处有
3
条棱,每条棱都有
2
个顶点,所以有2×E=3×V.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有
30
条棱,
20
个顶点,每个顶点处有
3
条棱.
25.(8分)如图,左图为一个棱长为4的正方体,右图为左图的表面展开图(字在外表面上),请根据要求回答问题:
(1)面“成”的对面是面
“爱”
;
(2)如果面“丽”在右面,面“美”在后面,面
“成”
会在上面;
(3)左图中,M,N为所在棱的中点,试在右图中画出点M,N的位置;右图中三角形AMN的面积为
18或10
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
