沪科版数学九年级上册第24章 圆 证明圆的切线的常用方法课件(31张ppt)
文档属性
| 名称 | 沪科版数学九年级上册第24章 圆 证明圆的切线的常用方法课件(31张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览







文档简介
HK版九年级下
阶段核心方法
证明圆的切线的常用方法
第24章 圆
4
提示:点击 进入习题
答案显示
1
2
3
5
见习题
见习题
见习题
6
见习题
见习题
见习题
7
见习题
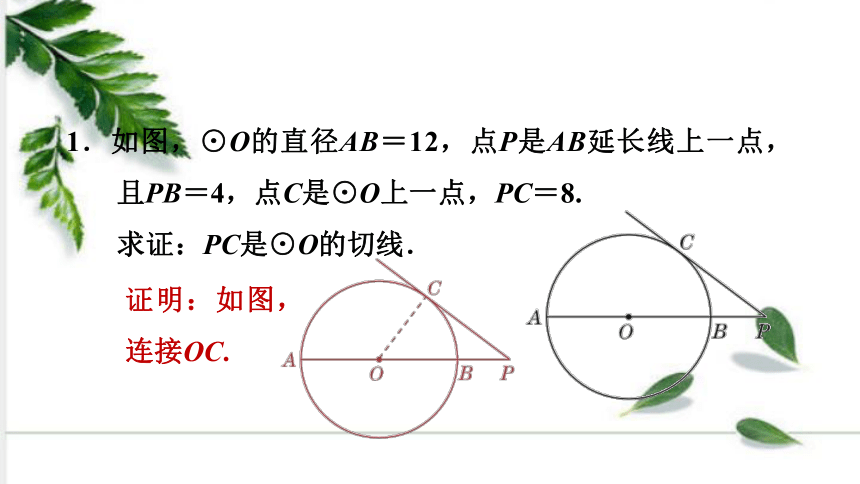
1.如图,⊙O的直径AB=12,点P是AB延长线上一点,且PB=4,点C是⊙O上一点,PC=8.
求证:PC是⊙O的切线.
证明:如图,连接OC.
∵⊙O的直径AB=12,∴OB=OC=6.
∵PB=4,∴PO=10.
在△POC中,PC2+CO2=82+62=100,PO2=102=100,
∴PC2+OC2=PO2.
∴∠OCP=90°,即OC⊥PC.
又∵OC是半径,∴PC是⊙O的切线.
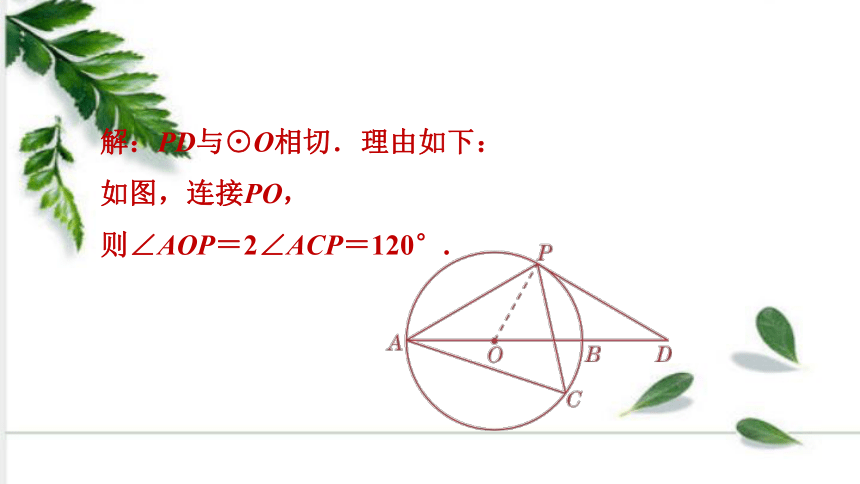
2.如图,以AB为直径的⊙O经过点P,C,且∠ACP=60°,D是AB延长线上一点,PA=PD.试判断PD与⊙O的位置关系,并说明理由.
解:PD与⊙O相切.理由如下:
如图,连接PO,
则∠AOP=2∠ACP=120°.
∵OA=OP,∴∠OAP=∠OPA=30°.
∵PA=PD,∴∠OAP=∠D=30°.
∴∠OPD=180°-∠OAP-∠OPA-∠D=90°,
即OP⊥PD.
又∵OP是半径,∴PD与⊙O相切.
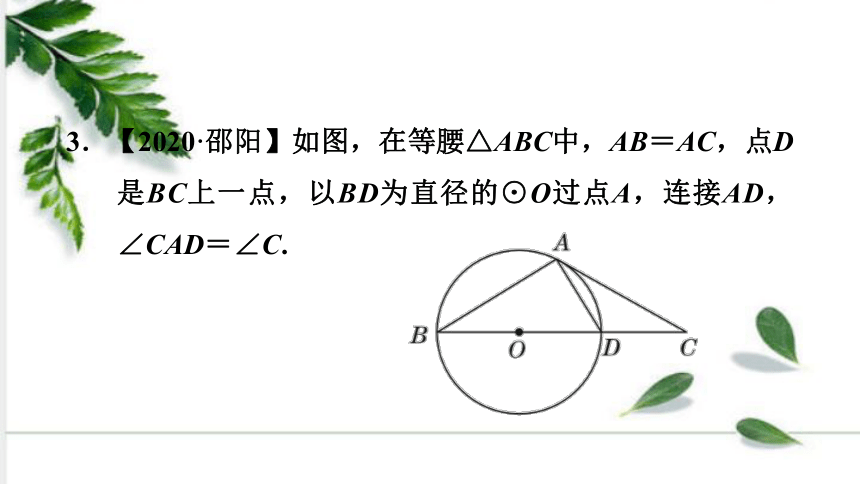
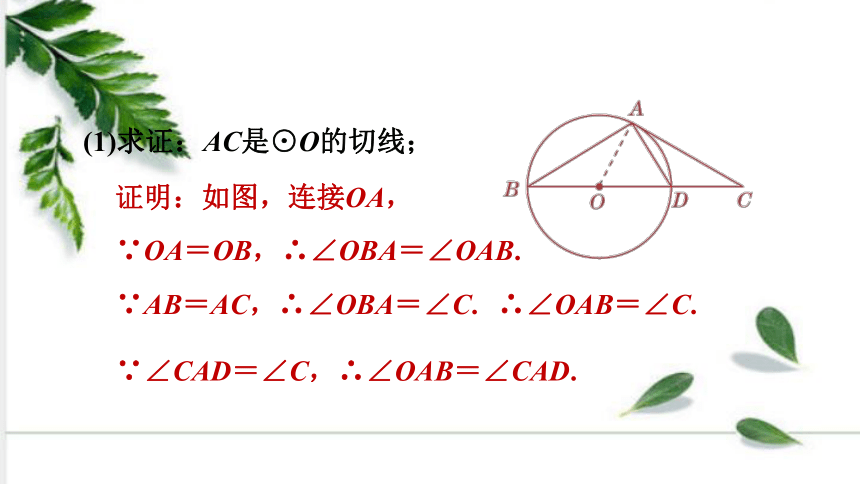
3.【2020·邵阳】如图,在等腰△ABC中,AB=AC,点D是BC上一点,以BD为直径的⊙O过点A,连接AD,∠CAD=∠C.
(1)求证:AC是⊙O的切线;
证明:如图,连接OA,
∵OA=OB,∴∠OBA=∠OAB.
∵AB=AC,∴∠OBA=∠C. ∴∠OAB=∠C.
∵∠CAD=∠C,∴∠OAB=∠CAD.
∵BD是直径,∴∠BAD=90°.
∵∠OAC=∠BAD-∠OAB+∠CAD=90°,
∴AC是⊙O的切线.
(2)若AC=4,求⊙O的半径.
解:由(1)可知AC是⊙O的切线,∴∠OAC=90°.
∵AB=AC,∴∠B=∠C.
∵∠AOD=2∠B,
∴∠AOC+∠C=2∠B+∠C=3∠C=90°.
∴∠B=∠C=30°.
4.【2020·衡阳】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点A和点D的圆,圆心O在线段AB上,⊙O交AB于点E,交AC于点F.
(1)判断BC与⊙O的位置关系,并说明理由;
解:BC与⊙O相切.理由如下:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠ODA=∠CAD.∴OD∥AC.
∵∠C=90°,∴∠ODC=90°.∴OD⊥BC.
又∵OD为半径,∴BC与⊙O相切.
(2)若AD=8,AE=10,求BD的长.
解:如图,连接DE.
∵AE是⊙O的直径,AE=10,
∴∠ADE=90°,OA=OE=OD=5.
∵∠C=90°,∴∠ADE=∠C.
5.已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP.
(1)求证:PC是⊙O的切线.
证明:如图,连接OC,
∵PB是⊙O的切线,∴∠OBP=90°.
∵OA=OC,∴∠OAC=∠OCA.
∵AC∥OP,∴∠OAC=∠POB,∠POC=∠OCA.
∴∠POB=∠POC.
∵OC=OB,OP=OP,∴△POC≌△POB(SAS).
∴∠OBP=∠OCP=90°,即OC⊥PC.
又∵OC是半径,∴PC是⊙O的切线.
(2)若∠A=60°,AB=4,求PC的长.
解:∵AB=4,∴OB=2.
6.如图,在梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B.
求证:CD与⊙O相切.
证明:如图,过点O作OH⊥CD于点H.
∵AE⊥BC,∴∠AEB=90°.
∵AD∥BC,∴∠DAO=∠AEB=90°,即OA⊥DA.
∵DO平分∠ADC,OH⊥DC,OA⊥DA,∴OH=OA.
又∵OH⊥DC,∴DC是⊙O的切线,
即CD与⊙O相切.
7.【中考·江西】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO的延长线于点D,
且∠AOD=∠BAD.
(1)求证:AB为⊙O的切线.
证明:如图,作OE⊥AB于点E.
∵⊙O与BC相切于点C,∴AC⊥BC.
谢谢!
阶段核心方法
证明圆的切线的常用方法
第24章 圆
4
提示:点击 进入习题
答案显示
1
2
3
5
见习题
见习题
见习题
6
见习题
见习题
见习题
7
见习题
1.如图,⊙O的直径AB=12,点P是AB延长线上一点,且PB=4,点C是⊙O上一点,PC=8.
求证:PC是⊙O的切线.
证明:如图,连接OC.
∵⊙O的直径AB=12,∴OB=OC=6.
∵PB=4,∴PO=10.
在△POC中,PC2+CO2=82+62=100,PO2=102=100,
∴PC2+OC2=PO2.
∴∠OCP=90°,即OC⊥PC.
又∵OC是半径,∴PC是⊙O的切线.
2.如图,以AB为直径的⊙O经过点P,C,且∠ACP=60°,D是AB延长线上一点,PA=PD.试判断PD与⊙O的位置关系,并说明理由.
解:PD与⊙O相切.理由如下:
如图,连接PO,
则∠AOP=2∠ACP=120°.
∵OA=OP,∴∠OAP=∠OPA=30°.
∵PA=PD,∴∠OAP=∠D=30°.
∴∠OPD=180°-∠OAP-∠OPA-∠D=90°,
即OP⊥PD.
又∵OP是半径,∴PD与⊙O相切.
3.【2020·邵阳】如图,在等腰△ABC中,AB=AC,点D是BC上一点,以BD为直径的⊙O过点A,连接AD,∠CAD=∠C.
(1)求证:AC是⊙O的切线;
证明:如图,连接OA,
∵OA=OB,∴∠OBA=∠OAB.
∵AB=AC,∴∠OBA=∠C. ∴∠OAB=∠C.
∵∠CAD=∠C,∴∠OAB=∠CAD.
∵BD是直径,∴∠BAD=90°.
∵∠OAC=∠BAD-∠OAB+∠CAD=90°,
∴AC是⊙O的切线.
(2)若AC=4,求⊙O的半径.
解:由(1)可知AC是⊙O的切线,∴∠OAC=90°.
∵AB=AC,∴∠B=∠C.
∵∠AOD=2∠B,
∴∠AOC+∠C=2∠B+∠C=3∠C=90°.
∴∠B=∠C=30°.
4.【2020·衡阳】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点A和点D的圆,圆心O在线段AB上,⊙O交AB于点E,交AC于点F.
(1)判断BC与⊙O的位置关系,并说明理由;
解:BC与⊙O相切.理由如下:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠ODA=∠CAD.∴OD∥AC.
∵∠C=90°,∴∠ODC=90°.∴OD⊥BC.
又∵OD为半径,∴BC与⊙O相切.
(2)若AD=8,AE=10,求BD的长.
解:如图,连接DE.
∵AE是⊙O的直径,AE=10,
∴∠ADE=90°,OA=OE=OD=5.
∵∠C=90°,∴∠ADE=∠C.
5.已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP.
(1)求证:PC是⊙O的切线.
证明:如图,连接OC,
∵PB是⊙O的切线,∴∠OBP=90°.
∵OA=OC,∴∠OAC=∠OCA.
∵AC∥OP,∴∠OAC=∠POB,∠POC=∠OCA.
∴∠POB=∠POC.
∵OC=OB,OP=OP,∴△POC≌△POB(SAS).
∴∠OBP=∠OCP=90°,即OC⊥PC.
又∵OC是半径,∴PC是⊙O的切线.
(2)若∠A=60°,AB=4,求PC的长.
解:∵AB=4,∴OB=2.
6.如图,在梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B.
求证:CD与⊙O相切.
证明:如图,过点O作OH⊥CD于点H.
∵AE⊥BC,∴∠AEB=90°.
∵AD∥BC,∴∠DAO=∠AEB=90°,即OA⊥DA.
∵DO平分∠ADC,OH⊥DC,OA⊥DA,∴OH=OA.
又∵OH⊥DC,∴DC是⊙O的切线,
即CD与⊙O相切.
7.【中考·江西】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径作圆,与BC相切于点C,过点A作AD⊥BO的延长线于点D,
且∠AOD=∠BAD.
(1)求证:AB为⊙O的切线.
证明:如图,作OE⊥AB于点E.
∵⊙O与BC相切于点C,∴AC⊥BC.
谢谢!
