人教版八年级上数学课件 11.2.1 第2课时 直角三角形的性质和判定(共19张PPT)
文档属性
| 名称 | 人教版八年级上数学课件 11.2.1 第2课时 直角三角形的性质和判定(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 687.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-17 10:12:46 | ||
图片预览




文档简介
(共19张PPT)
第1课时
直角三角形的性质和判断
葫芦岛第六初级中学
我们常用的三角板,两锐角的度数之和为多少度?
30°+60°=90°
45°+45°=90°
如图,在Rt△ABC中,
∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为
∠C=90°,由三角形内角和定理,得∠A
+∠B+∠C=90°,即
∠A
+∠B=90°.
?思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
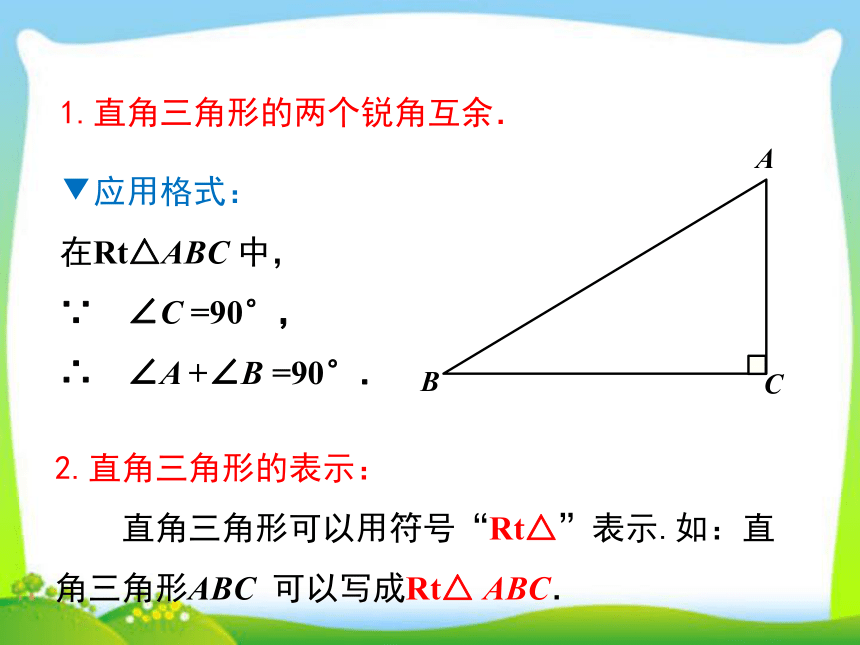
1.直角三角形的两个锐角互余.
▼应用格式:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
2.直角三角形的表示:
直角三角形可以用符号“Rt△”表示.如:直角三角形ABC
可以写成Rt△
ABC.
解:方法一(利用平行的判定和性质)
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质)
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
(1)如图1,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
图1
例1
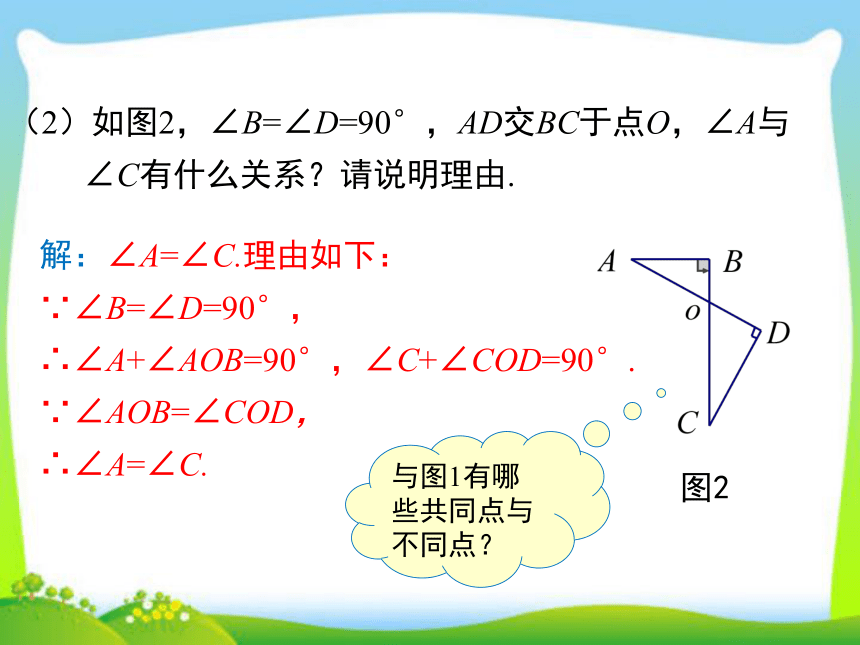
解:∠A=∠C.理由如下:
∵∠B=∠D=90°,
∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠C.
(2)如图2,∠B=∠D=90°,AD交BC于点O,∠A与
∠C有什么关系?请说明理由.
图2
与图1有哪些共同点与不同点?
如图,
∠C=∠D=90
°,AD、BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,
∠CAE=90
°-
∠AEC.
在Rt△BDE中,
∠DBE=90
°-
∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
例2
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.
【变式题】如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点F,∠A与∠BFC又有什么关系?为什么?
?思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
∠A=∠D
有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC
是直角三角形吗?
在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
A
B
C
▼应用格式:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
有两个角互余的三角形是直角三角形.
如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
例3
如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
例4
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
2.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第1题
第2题
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
4.在一个直角三角形中,有一个锐角等于40°,则另
一个锐角的度数是( )
A.40°
B.50°
C.60°
D.70°
B
5.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
6.如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
C
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
课堂总结
第1课时
直角三角形的性质和判断
葫芦岛第六初级中学
我们常用的三角板,两锐角的度数之和为多少度?
30°+60°=90°
45°+45°=90°
如图,在Rt△ABC中,
∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为
∠C=90°,由三角形内角和定理,得∠A
+∠B+∠C=90°,即
∠A
+∠B=90°.
?思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
1.直角三角形的两个锐角互余.
▼应用格式:
在Rt△ABC
中,
∵ ∠C
=90°,
∴ ∠A
+∠B
=90°.
2.直角三角形的表示:
直角三角形可以用符号“Rt△”表示.如:直角三角形ABC
可以写成Rt△
ABC.
解:方法一(利用平行的判定和性质)
∵∠B=∠C=90°,
∴AB∥CD,
∴∠A=∠D.
方法二(利用直角三角形的性质)
∵∠B=∠C=90°,
∴∠A+∠AOB=90°,∠D+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠D.
(1)如图1,∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?
图1
例1
解:∠A=∠C.理由如下:
∵∠B=∠D=90°,
∴∠A+∠AOB=90°,∠C+∠COD=90°.
∵∠AOB=∠COD,
∴∠A=∠C.
(2)如图2,∠B=∠D=90°,AD交BC于点O,∠A与
∠C有什么关系?请说明理由.
图2
与图1有哪些共同点与不同点?
如图,
∠C=∠D=90
°,AD、BC相交于点E.
∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△ACE中,
∠CAE=90
°-
∠AEC.
在Rt△BDE中,
∠DBE=90
°-
∠BED.
∵
∠AEC=
∠BED,
∴
∠CAE=
∠DBE.
例2
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.
【变式题】如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点F,∠A与∠BFC又有什么关系?为什么?
?思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
∠A=∠D
有两个角互余的三角形是直角三角形吗?
如图,在△ABC中,
∠A
+∠B=90°
,
那么△ABC
是直角三角形吗?
在△ABC中,因为
∠A
+∠B
+∠C=180°,
又∠A
+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
A
B
C
▼应用格式:
在△ABC
中,
∵ ∠A
+∠B
=90°,
∴ △ABC
是直角三角形.
有两个角互余的三角形是直角三角形.
如图,∠C=90
°,
∠1=
∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+
∠A=90
°.
∵
∠1=
∠2,
∴∠1
+
∠A=90
°.
即△ADE是直角三角形.
例3
如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?
解:△ABD是直角三角形.理由如下:
∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
例4
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
2.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第1题
第2题
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
4.在一个直角三角形中,有一个锐角等于40°,则另
一个锐角的度数是( )
A.40°
B.50°
C.60°
D.70°
B
5.具备下列条件的△ABC中,不是直角三角形的是
(
)
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
6.如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B
B.∠A
C.∠BCD和∠A
D.∠BCD
C
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
课堂总结
