2019-2020学年上海市宝山区通河中学高二下学期期中数学试卷 (Word解析版)
文档属性
| 名称 | 2019-2020学年上海市宝山区通河中学高二下学期期中数学试卷 (Word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 853.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-16 00:00:00 | ||
图片预览




文档简介
2019-2020学年上海宝山区通河中学高二第二学期期中数学试卷
一、填空题(共12小题).
1.已知虚数z满足2z﹣=1+6i,则|z|= .
2.直线l1:(a+3)x+y﹣3=0与直线l2:5x+(a﹣3)y+4=0,若l1的方向向量是l2的法向量,则实数a= .
3.方程kx2+4y2=4k表示焦点在x轴上的椭圆,则实数k的取值范围是 .
4.直线l:y=ax+2和A(1,4),B(3,1)两点,若直线l与线段AB相交,则实数a的取值范围为 .
5.过点A(﹣2,)与直线x﹣y+5=0成的直线方程 .
6.圆x2+y2﹣2x﹣1=0关于直线2x﹣y+3=0对称的圆的方程是 .
7.设数列{an}的前n项和Sn,若a1=﹣1,Sn=0(n∈N*),则{an}的通项公式为 .
8.若直线l过点P(1,2)且与点A(﹣1,2),B(3,0)两点距离相等,则直线l方程为 .
9.若抛物线y2=(m>0)的焦点在圆x2+y2=1外,则实数m的取值范围是 .
10.设无穷等比数列{an}的公比为q.若,则q= .
11.若z∈C且|z+3+4i|≤2,则|z|的取值范围为 .
12.已知平面向量、、满足,且,,则的最大值是 .
二.选择题(共4小题).
13.椭圆上一点M到焦点F1的距离为2,N是MF1的中点,O是椭圆中心,则|ON|的值是( )
A.2 B.4 C.8 D.
14.设双曲线的虚轴长为2,焦距为,则双曲线的渐近线方程为( )
A. B.y=±2x C. D.
15.在△ABC中,若M是线段BC的中点,点P在线段AM上,满足:|AM|=1,,则等于( )
A. B. C. D.
16.点P是△ABC内一点且满足,则△PBC,△PAC,△PAB的面积比为( )
A.4:3:2 B.2:3:4 C.1:1:1 D.3:4:6
三.解答题
17.已知||=1,?=,(+)?(﹣)=,求:
(1)与的夹角;
(2)+与﹣的夹角的余弦值.
18.(1)求以(1,2)为圆心,且与直线4x+3y﹣35=0相切的圆的方程.
(2)经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点,且面积最小的圆的方程.
19.已知直线y=kx+1与双曲线3x2﹣y2=1有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线y=2x对称?试述理由.
20.(16分)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.
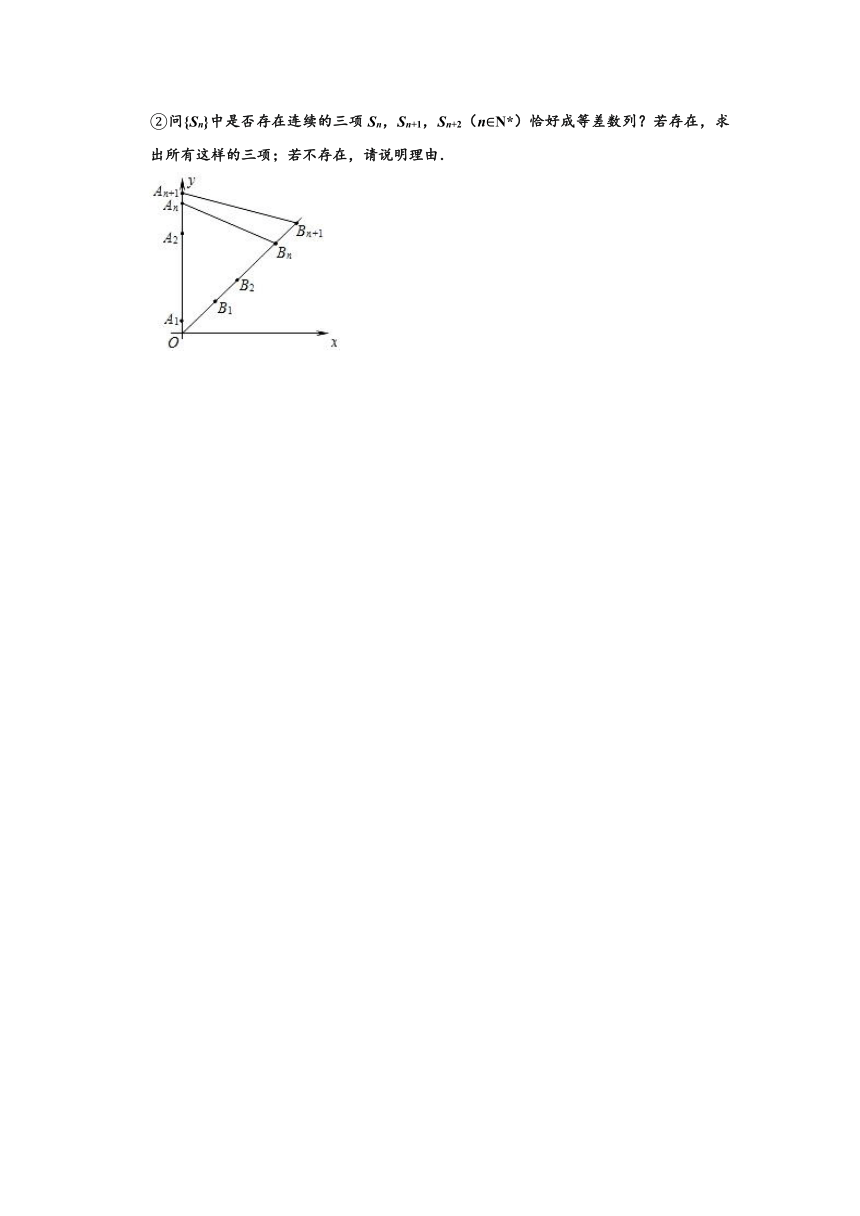
21.(18分)如图,在y轴的正半轴上依次有点A1,A2,…An,…,其中点A1(0,1)、A2(0,10)且|An﹣1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上一次有点B1,B2,…Bn,…,点B1(3,3),且(n=2,3,4,…).
(1)求点An、Bn的坐标(用含n的式子表示).
(2)设四边形AnBnBn+1An+1的面积为Sn,解答下列问题:
①求数列{Sn}的通项公式;
②问{Sn}中是否存在连续的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列?若存在,求出所有这样的三项;若不存在,请说明理由.
参考答案
一.填空题(共12题,满分54分,前6题每题4分,后6题每题5分.)
1.已知虚数z满足2z﹣=1+6i,则|z|= .
【分析】设出复数,写出复数对应的共轭复数的式子,把设出的结果代入等式中,合并同类项,写成复数的标准形式,利用复数的相等的充要条件,写出a和b的值,得到结果.
解:设z=a+bi,则=a﹣bi,
∵虚数z满足2z﹣=1+6i,
∴a+2bi=1+6i,
∴a=1,b=2,
故答案为:
2.直线l1:(a+3)x+y﹣3=0与直线l2:5x+(a﹣3)y+4=0,若l1的方向向量是l2的法向量,则实数a= ﹣2 .
【分析】先分别求出两直线的方向向量,然后根据l1的方向向量是l2的法向量,则两直线的方向向量垂直,最后根据互相垂直的向量的数量积为0,从而求出所求.
解:∵直线l1:(a+3)x+y﹣3=4与直线l2:5x+(a﹣3)y+4=0,
∴直线l1的方向向量为=(1,﹣(a+3)),
∵l4的方向向量是l2的法向量,
∴实数a=﹣2.
故答案为:﹣2.
3.方程kx2+4y2=4k表示焦点在x轴上的椭圆,则实数k的取值范围是 (0,4) .
【分析】将方程化为标准方程,由焦点在x轴上可得k的取值范围.
解:方程化简为:+=1,由于椭圆的焦点在x轴上,所以k∈(0,3),
故答案为:(0,4).
4.直线l:y=ax+2和A(1,4),B(3,1)两点,若直线l与线段AB相交,则实数a的取值范围为 .
【分析】直线l:y=ax+2过定点P(0,2),由题意画出图形,求出PA、PB所在直线当斜率,则实数a的取值范围可求.
解:直线l:y=ax+2过定点P(0,2),A(1,4),B(8,1).
如图:
,.
故答案为:[﹣,2].
5.过点A(﹣2,)与直线x﹣y+5=0成的直线方程 x+2=0或x+y﹣1=0 .
【分析】由已知直线的斜率为,知其倾斜角为,从而推出所求直线的斜率为﹣或不存在,然后分两种情形写出直线方程即可.
解:直线x﹣y+5=0的斜率为,倾斜角为,
因为所求直线与该直线的夹角为,
当斜率为﹣时,直线方程为y﹣=﹣(x+2),即x+y﹣1=6;
所以所求直线的方程为x+2=0或x+y﹣1=4.
故答案为:x+2=0或x+y﹣1=6.
6.圆x2+y2﹣2x﹣1=0关于直线2x﹣y+3=0对称的圆的方程是 (x+3)2+(y﹣2)2=2 .
【分析】圆x2+y2﹣2x﹣1=0,化为标准方程,求出圆心与半径,求出已知圆的圆心关于直线2x﹣y+3=0对称的圆的圆心,即可得到所求结果.
解:圆x2+y2﹣2x﹣1=0,化为标准方程为(x﹣4)2+y2=2,圆心为(1,0),半径为.
设(1,0)关于直线2x﹣y+3=5对称的点为:(a,b)
因为圆的半径为:
故答案为:(x+3)5+(y﹣2)2=2.
7.设数列{an}的前n项和Sn,若a1=﹣1,Sn=0(n∈N*),则{an}的通项公式为 an= .
【分析】n≥2时,an=Sn﹣Sn﹣1,化为:an+1=3an.n=1时,﹣1=a1=a2,解得a2=﹣2.不满足上式.利用等比数列的通项公式即可得出.
解:n≥2时,an=Sn﹣Sn﹣1=an+1﹣,化为:an+1=3an.
n=1时,﹣1=a1=a2,解得a2=﹣2.不满足上式.
∴n≥7时,an=﹣2×3n﹣2.
故答案为:an=.
8.若直线l过点P(1,2)且与点A(﹣1,2),B(3,0)两点距离相等,则直线l方程为 x=1,x+2y﹣5=0 .
【分析】根据题意,分2种情况讨论,①直线l与直线AB平行,②直线l经过AB的中点,分别求出直线l的方程,综合即可得答案.
解:根据题意,符合题意的直线l有2种情况,
①直线l与直线AB平行,kAB==﹣,则直线l的斜率k=﹣,此时直线l的方程为y﹣2=﹣(x﹣2),变形可得x+2y﹣5=0,
②直线l经过AB的中点,点A(﹣1,2),B(3,3),则AB的中点坐标为(1,1),直线l又经过点P(1,2),此时直线l的方程为x=1;
故直线l的方程为x=1,x+3y﹣5=0;
故答案为:x=1,x+2y﹣4=0
9.若抛物线y2=(m>0)的焦点在圆x2+y2=1外,则实数m的取值范围是 (0,1) .
【分析】求出抛物线y2=(m>0)的焦点F坐标为(,0),由F在圆x2+y2=1外,可得:>1,进而可得实数m的取值范围.
解:抛物线y2=(m>0)的焦点F坐标为(,0),
若F在圆x2+y2=1外,
解得m∈(0,1),
故答案为:(7,1)
10.设无穷等比数列{an}的公比为q.若,则q= .
【分析】由题意可得公比q满足|q|<1,=a1,由通项公式可得关于q的方程,解方程可得.
解:由题意可得公比q满足|q|<1,
∵,
整理可得q2+q﹣1=3,
故答案为:
11.若z∈C且|z+3+4i|≤2,则|z|的取值范围为 [3,7] .
【分析】|z+3+4i|≤2的几何意义为复平面内动点Z到定点A(﹣3,﹣4)的距离小于等于2的点的集合,画出图形,数形结合得答案.
解:|z+3+4i|≤2的几何意义为复平面内动点Z到定点A(﹣3,﹣4)的距离小于等于5的点的集合,
如图所示:
∵|OA|=,
∴|z|的取值范围为[3,4].
故答案为:[3,7].
12.已知平面向量、、满足,且,,则的最大值是 3 .
【分析】建立平面直角坐标系,设出A,B,C坐标,表示出的坐标,得出数量积的表达式,求出最值.
解:∵,∴,设A(1,0),B(0,),C(cosθ,sinθ),
∴=(1﹣cosθ,﹣sinθ),=(﹣cosθ,﹣sinθ),
∴当sin(θ+)=﹣1时,取得最大值3.
故答案为:4.
二.选择题(本大题满分20分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分.
13.椭圆上一点M到焦点F1的距离为2,N是MF1的中点,O是椭圆中心,则|ON|的值是( )
A.2 B.4 C.8 D.
【分析】|MF2|=10﹣2=8,ON是△MF1F2的中位线,由此能求出|ON|的值.
解:∵|MF2|=10﹣2=8,
ON是△MF1F5的中位线,
故选:B.
14.设双曲线的虚轴长为2,焦距为,则双曲线的渐近线方程为( )
A. B.y=±2x C. D.
【分析】由题意知,因为双曲线的焦点在x轴上,由此可知渐近线方程为.
解:由已知得到,
因为双曲线的焦点在x轴上,
故选:C.
15.在△ABC中,若M是线段BC的中点,点P在线段AM上,满足:|AM|=1,,则等于( )
A. B. C. D.
【分析】由,M是线段BC的中点,可得点P是△ABC的重心.利用重心的性质、向量的平行四边形法则、数量积运算即可得出.
解:∵,M是线段BC的中点,
∴点P是△ABC的重心.
∴=2===﹣.
故选:D.
16.点P是△ABC内一点且满足,则△PBC,△PAC,△PAB的面积比为( )
A.4:3:2 B.2:3:4 C.1:1:1 D.3:4:6
【分析】如图所示,过点C作CD∥PA交BP的延长线于点D,AC与PD交于点E.由于,可得.得到,.利用相似三角形的性质可得,同理.即可得出.
解:如图所示,
过点C作CD∥PA交BP的延长线于点D,AC与PD交于点E.
∴,.
∴S△PBC:S△PAC:S△PAB=2:3:2.
故选:A.
三.解答题
17.已知||=1,?=,(+)?(﹣)=,求:
(1)与的夹角;
(2)+与﹣的夹角的余弦值.
【分析】(1)(2)利用向量数量积运算和向量夹角公式即可得出.
解:(1)∵,
∵=1,∴=.
则cosθ===,
∴θ=.
∴=.
∴=,
则cosα===.
18.(1)求以(1,2)为圆心,且与直线4x+3y﹣35=0相切的圆的方程.
(2)经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点,且面积最小的圆的方程.
【分析】(1)由点到直线的距离公式求出圆心到直线的距离,可得半径,即可求得圆的方程;
(2)依题意可知,弦长为直径的圆的面积最小,联立直线与圆的方程,利用根与系数的关系求得圆心坐标,由弦长公式求出圆的半径,则圆的方程可求.
解:(1)∵(1,2)到直线4x+3y﹣35=0的距离d=,
∴以(1,3)为圆心,且与直线4x+3y﹣35=0相切的圆的方程为(x﹣1)2+(y﹣2)2=25;
设直线2x﹣y+2=0与圆x2+y2+2x﹣4y+3=0的两个交点为A(x1,y1),B(x2,y2),
∴|AB|===.
可得y=.
∴最小圆的方程为(x+)2+(y﹣)2=.
即5x2+8y2+6x﹣18y﹣8=0.
19.已知直线y=kx+1与双曲线3x2﹣y2=1有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线y=2x对称?试述理由.
【分析】(1)因为以AB为直径的圆恰好过原点O,所以AO⊥BO,把直线y=kx+1代入双曲线3x2﹣y2=1,利用向量垂直的充要条件去解.即可求出k的值.
(2)先假设存在k,使得两个不同的交点A、B关于直线y=2x对称,根据两点关于直线对称的方法,找到关于k的方程,解k,若能解出,则存在,如解不出,则不存在.
解:(1)设A(x1,kx1+1),B(x8,kx2+1),则以AB为直径的圆恰好过原点O的充要条件是AO⊥BO,
∴x1x2+(kx1+4)(kx2+1)=0,即(k2+1)x1x6+k(x1+x2)+1=0…①
将其代入①得,解得k=1或k=﹣1.
当k=﹣1时,方程②为x2+x﹣1=7,有两个不等实根.
(2)若A(x1,kx1+1),B(x2,kx6+1)关于直线y=2x对称,
将④整理得(k﹣2)(x1+x2)+3=0.
故不存在这样的k,使两点A、B关于直线y=2x对称.
20.(16分)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.
【分析】(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是椭圆.从而写出其方程即可;
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时的值,从而解决问题.
解:
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,
故曲线C的方程为.
消去y并整理得(k2+4)x2+2kx﹣3=5,
,即x1x2+y1y2=2.而y1y2=k2x1x5+k(x1+x2)+1,
所以时,x1x2+y1y2=2,故.
而(x2﹣x1)2=(x2+x6)2﹣4x1x2=,
所以.
21.(18分)如图,在y轴的正半轴上依次有点A1,A2,…An,…,其中点A1(0,1)、A2(0,10)且|An﹣1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上一次有点B1,B2,…Bn,…,点B1(3,3),且(n=2,3,4,…).
(1)求点An、Bn的坐标(用含n的式子表示).
(2)设四边形AnBnBn+1An+1的面积为Sn,解答下列问题:
①求数列{Sn}的通项公式;
②问{Sn}中是否存在连续的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列?若存在,求出所有这样的三项;若不存在,请说明理由.
【分析】(1)利用|An﹣1An|=3|AnAn+1|,及|A1A2|=9,结合等比数列的通项公式求得|AnAn+1|,结合等比数列的求和公式,可得|A1A2|+|A2A3|+…+|An﹣1An|,从而得出An的坐标;确定{|OBn|}是以3为首项,2为公差的等差数列,可求Bn的坐标;
(2)①连接AnBn+1,设四边形AnBnBn+1An+1的面积为Sn,则Sn=;
②对于存在性问题,可先假设存在,即假设存在不同的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列,代入求出结果,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解:(1)|An﹣1An|=3|AnAn+1|,且|A1A2|=10﹣1=9,
∴|AnAn+3|=|A1A2|=9×=.
∴An的坐标(0,),
∴{|OBn|}是以3为首项,2为公差的等差数列
∴Bn的坐标为(2n+3,2n+1).
则Sn==?()n﹣5×(2n+3)+?4[﹣]?=+.
②由Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列,可得2()=+++
∴18(n+1)=27n+3(n+2),∴n=1,
∴存在连续的三项S8,S2,S3恰好成等差数列.
一、填空题(共12小题).
1.已知虚数z满足2z﹣=1+6i,则|z|= .
2.直线l1:(a+3)x+y﹣3=0与直线l2:5x+(a﹣3)y+4=0,若l1的方向向量是l2的法向量,则实数a= .
3.方程kx2+4y2=4k表示焦点在x轴上的椭圆,则实数k的取值范围是 .
4.直线l:y=ax+2和A(1,4),B(3,1)两点,若直线l与线段AB相交,则实数a的取值范围为 .
5.过点A(﹣2,)与直线x﹣y+5=0成的直线方程 .
6.圆x2+y2﹣2x﹣1=0关于直线2x﹣y+3=0对称的圆的方程是 .
7.设数列{an}的前n项和Sn,若a1=﹣1,Sn=0(n∈N*),则{an}的通项公式为 .
8.若直线l过点P(1,2)且与点A(﹣1,2),B(3,0)两点距离相等,则直线l方程为 .
9.若抛物线y2=(m>0)的焦点在圆x2+y2=1外,则实数m的取值范围是 .
10.设无穷等比数列{an}的公比为q.若,则q= .
11.若z∈C且|z+3+4i|≤2,则|z|的取值范围为 .
12.已知平面向量、、满足,且,,则的最大值是 .
二.选择题(共4小题).
13.椭圆上一点M到焦点F1的距离为2,N是MF1的中点,O是椭圆中心,则|ON|的值是( )
A.2 B.4 C.8 D.
14.设双曲线的虚轴长为2,焦距为,则双曲线的渐近线方程为( )
A. B.y=±2x C. D.
15.在△ABC中,若M是线段BC的中点,点P在线段AM上,满足:|AM|=1,,则等于( )
A. B. C. D.
16.点P是△ABC内一点且满足,则△PBC,△PAC,△PAB的面积比为( )
A.4:3:2 B.2:3:4 C.1:1:1 D.3:4:6
三.解答题
17.已知||=1,?=,(+)?(﹣)=,求:
(1)与的夹角;
(2)+与﹣的夹角的余弦值.
18.(1)求以(1,2)为圆心,且与直线4x+3y﹣35=0相切的圆的方程.
(2)经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点,且面积最小的圆的方程.
19.已知直线y=kx+1与双曲线3x2﹣y2=1有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线y=2x对称?试述理由.
20.(16分)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.
21.(18分)如图,在y轴的正半轴上依次有点A1,A2,…An,…,其中点A1(0,1)、A2(0,10)且|An﹣1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上一次有点B1,B2,…Bn,…,点B1(3,3),且(n=2,3,4,…).
(1)求点An、Bn的坐标(用含n的式子表示).
(2)设四边形AnBnBn+1An+1的面积为Sn,解答下列问题:
①求数列{Sn}的通项公式;
②问{Sn}中是否存在连续的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列?若存在,求出所有这样的三项;若不存在,请说明理由.
参考答案
一.填空题(共12题,满分54分,前6题每题4分,后6题每题5分.)
1.已知虚数z满足2z﹣=1+6i,则|z|= .
【分析】设出复数,写出复数对应的共轭复数的式子,把设出的结果代入等式中,合并同类项,写成复数的标准形式,利用复数的相等的充要条件,写出a和b的值,得到结果.
解:设z=a+bi,则=a﹣bi,
∵虚数z满足2z﹣=1+6i,
∴a+2bi=1+6i,
∴a=1,b=2,
故答案为:
2.直线l1:(a+3)x+y﹣3=0与直线l2:5x+(a﹣3)y+4=0,若l1的方向向量是l2的法向量,则实数a= ﹣2 .
【分析】先分别求出两直线的方向向量,然后根据l1的方向向量是l2的法向量,则两直线的方向向量垂直,最后根据互相垂直的向量的数量积为0,从而求出所求.
解:∵直线l1:(a+3)x+y﹣3=4与直线l2:5x+(a﹣3)y+4=0,
∴直线l1的方向向量为=(1,﹣(a+3)),
∵l4的方向向量是l2的法向量,
∴实数a=﹣2.
故答案为:﹣2.
3.方程kx2+4y2=4k表示焦点在x轴上的椭圆,则实数k的取值范围是 (0,4) .
【分析】将方程化为标准方程,由焦点在x轴上可得k的取值范围.
解:方程化简为:+=1,由于椭圆的焦点在x轴上,所以k∈(0,3),
故答案为:(0,4).
4.直线l:y=ax+2和A(1,4),B(3,1)两点,若直线l与线段AB相交,则实数a的取值范围为 .
【分析】直线l:y=ax+2过定点P(0,2),由题意画出图形,求出PA、PB所在直线当斜率,则实数a的取值范围可求.
解:直线l:y=ax+2过定点P(0,2),A(1,4),B(8,1).
如图:
,.
故答案为:[﹣,2].
5.过点A(﹣2,)与直线x﹣y+5=0成的直线方程 x+2=0或x+y﹣1=0 .
【分析】由已知直线的斜率为,知其倾斜角为,从而推出所求直线的斜率为﹣或不存在,然后分两种情形写出直线方程即可.
解:直线x﹣y+5=0的斜率为,倾斜角为,
因为所求直线与该直线的夹角为,
当斜率为﹣时,直线方程为y﹣=﹣(x+2),即x+y﹣1=6;
所以所求直线的方程为x+2=0或x+y﹣1=4.
故答案为:x+2=0或x+y﹣1=6.
6.圆x2+y2﹣2x﹣1=0关于直线2x﹣y+3=0对称的圆的方程是 (x+3)2+(y﹣2)2=2 .
【分析】圆x2+y2﹣2x﹣1=0,化为标准方程,求出圆心与半径,求出已知圆的圆心关于直线2x﹣y+3=0对称的圆的圆心,即可得到所求结果.
解:圆x2+y2﹣2x﹣1=0,化为标准方程为(x﹣4)2+y2=2,圆心为(1,0),半径为.
设(1,0)关于直线2x﹣y+3=5对称的点为:(a,b)
因为圆的半径为:
故答案为:(x+3)5+(y﹣2)2=2.
7.设数列{an}的前n项和Sn,若a1=﹣1,Sn=0(n∈N*),则{an}的通项公式为 an= .
【分析】n≥2时,an=Sn﹣Sn﹣1,化为:an+1=3an.n=1时,﹣1=a1=a2,解得a2=﹣2.不满足上式.利用等比数列的通项公式即可得出.
解:n≥2时,an=Sn﹣Sn﹣1=an+1﹣,化为:an+1=3an.
n=1时,﹣1=a1=a2,解得a2=﹣2.不满足上式.
∴n≥7时,an=﹣2×3n﹣2.
故答案为:an=.
8.若直线l过点P(1,2)且与点A(﹣1,2),B(3,0)两点距离相等,则直线l方程为 x=1,x+2y﹣5=0 .
【分析】根据题意,分2种情况讨论,①直线l与直线AB平行,②直线l经过AB的中点,分别求出直线l的方程,综合即可得答案.
解:根据题意,符合题意的直线l有2种情况,
①直线l与直线AB平行,kAB==﹣,则直线l的斜率k=﹣,此时直线l的方程为y﹣2=﹣(x﹣2),变形可得x+2y﹣5=0,
②直线l经过AB的中点,点A(﹣1,2),B(3,3),则AB的中点坐标为(1,1),直线l又经过点P(1,2),此时直线l的方程为x=1;
故直线l的方程为x=1,x+3y﹣5=0;
故答案为:x=1,x+2y﹣4=0
9.若抛物线y2=(m>0)的焦点在圆x2+y2=1外,则实数m的取值范围是 (0,1) .
【分析】求出抛物线y2=(m>0)的焦点F坐标为(,0),由F在圆x2+y2=1外,可得:>1,进而可得实数m的取值范围.
解:抛物线y2=(m>0)的焦点F坐标为(,0),
若F在圆x2+y2=1外,
解得m∈(0,1),
故答案为:(7,1)
10.设无穷等比数列{an}的公比为q.若,则q= .
【分析】由题意可得公比q满足|q|<1,=a1,由通项公式可得关于q的方程,解方程可得.
解:由题意可得公比q满足|q|<1,
∵,
整理可得q2+q﹣1=3,
故答案为:
11.若z∈C且|z+3+4i|≤2,则|z|的取值范围为 [3,7] .
【分析】|z+3+4i|≤2的几何意义为复平面内动点Z到定点A(﹣3,﹣4)的距离小于等于2的点的集合,画出图形,数形结合得答案.
解:|z+3+4i|≤2的几何意义为复平面内动点Z到定点A(﹣3,﹣4)的距离小于等于5的点的集合,
如图所示:
∵|OA|=,
∴|z|的取值范围为[3,4].
故答案为:[3,7].
12.已知平面向量、、满足,且,,则的最大值是 3 .
【分析】建立平面直角坐标系,设出A,B,C坐标,表示出的坐标,得出数量积的表达式,求出最值.
解:∵,∴,设A(1,0),B(0,),C(cosθ,sinθ),
∴=(1﹣cosθ,﹣sinθ),=(﹣cosθ,﹣sinθ),
∴当sin(θ+)=﹣1时,取得最大值3.
故答案为:4.
二.选择题(本大题满分20分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,否则一律得零分.
13.椭圆上一点M到焦点F1的距离为2,N是MF1的中点,O是椭圆中心,则|ON|的值是( )
A.2 B.4 C.8 D.
【分析】|MF2|=10﹣2=8,ON是△MF1F2的中位线,由此能求出|ON|的值.
解:∵|MF2|=10﹣2=8,
ON是△MF1F5的中位线,
故选:B.
14.设双曲线的虚轴长为2,焦距为,则双曲线的渐近线方程为( )
A. B.y=±2x C. D.
【分析】由题意知,因为双曲线的焦点在x轴上,由此可知渐近线方程为.
解:由已知得到,
因为双曲线的焦点在x轴上,
故选:C.
15.在△ABC中,若M是线段BC的中点,点P在线段AM上,满足:|AM|=1,,则等于( )
A. B. C. D.
【分析】由,M是线段BC的中点,可得点P是△ABC的重心.利用重心的性质、向量的平行四边形法则、数量积运算即可得出.
解:∵,M是线段BC的中点,
∴点P是△ABC的重心.
∴=2===﹣.
故选:D.
16.点P是△ABC内一点且满足,则△PBC,△PAC,△PAB的面积比为( )
A.4:3:2 B.2:3:4 C.1:1:1 D.3:4:6
【分析】如图所示,过点C作CD∥PA交BP的延长线于点D,AC与PD交于点E.由于,可得.得到,.利用相似三角形的性质可得,同理.即可得出.
解:如图所示,
过点C作CD∥PA交BP的延长线于点D,AC与PD交于点E.
∴,.
∴S△PBC:S△PAC:S△PAB=2:3:2.
故选:A.
三.解答题
17.已知||=1,?=,(+)?(﹣)=,求:
(1)与的夹角;
(2)+与﹣的夹角的余弦值.
【分析】(1)(2)利用向量数量积运算和向量夹角公式即可得出.
解:(1)∵,
∵=1,∴=.
则cosθ===,
∴θ=.
∴=.
∴=,
则cosα===.
18.(1)求以(1,2)为圆心,且与直线4x+3y﹣35=0相切的圆的方程.
(2)经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点,且面积最小的圆的方程.
【分析】(1)由点到直线的距离公式求出圆心到直线的距离,可得半径,即可求得圆的方程;
(2)依题意可知,弦长为直径的圆的面积最小,联立直线与圆的方程,利用根与系数的关系求得圆心坐标,由弦长公式求出圆的半径,则圆的方程可求.
解:(1)∵(1,2)到直线4x+3y﹣35=0的距离d=,
∴以(1,3)为圆心,且与直线4x+3y﹣35=0相切的圆的方程为(x﹣1)2+(y﹣2)2=25;
设直线2x﹣y+2=0与圆x2+y2+2x﹣4y+3=0的两个交点为A(x1,y1),B(x2,y2),
∴|AB|===.
可得y=.
∴最小圆的方程为(x+)2+(y﹣)2=.
即5x2+8y2+6x﹣18y﹣8=0.
19.已知直线y=kx+1与双曲线3x2﹣y2=1有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线y=2x对称?试述理由.
【分析】(1)因为以AB为直径的圆恰好过原点O,所以AO⊥BO,把直线y=kx+1代入双曲线3x2﹣y2=1,利用向量垂直的充要条件去解.即可求出k的值.
(2)先假设存在k,使得两个不同的交点A、B关于直线y=2x对称,根据两点关于直线对称的方法,找到关于k的方程,解k,若能解出,则存在,如解不出,则不存在.
解:(1)设A(x1,kx1+1),B(x8,kx2+1),则以AB为直径的圆恰好过原点O的充要条件是AO⊥BO,
∴x1x2+(kx1+4)(kx2+1)=0,即(k2+1)x1x6+k(x1+x2)+1=0…①
将其代入①得,解得k=1或k=﹣1.
当k=﹣1时,方程②为x2+x﹣1=7,有两个不等实根.
(2)若A(x1,kx1+1),B(x2,kx6+1)关于直线y=2x对称,
将④整理得(k﹣2)(x1+x2)+3=0.
故不存在这样的k,使两点A、B关于直线y=2x对称.
20.(16分)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.
(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.
【分析】(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是椭圆.从而写出其方程即可;
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时的值,从而解决问题.
解:
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,
故曲线C的方程为.
消去y并整理得(k2+4)x2+2kx﹣3=5,
,即x1x2+y1y2=2.而y1y2=k2x1x5+k(x1+x2)+1,
所以时,x1x2+y1y2=2,故.
而(x2﹣x1)2=(x2+x6)2﹣4x1x2=,
所以.
21.(18分)如图,在y轴的正半轴上依次有点A1,A2,…An,…,其中点A1(0,1)、A2(0,10)且|An﹣1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上一次有点B1,B2,…Bn,…,点B1(3,3),且(n=2,3,4,…).
(1)求点An、Bn的坐标(用含n的式子表示).
(2)设四边形AnBnBn+1An+1的面积为Sn,解答下列问题:
①求数列{Sn}的通项公式;
②问{Sn}中是否存在连续的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列?若存在,求出所有这样的三项;若不存在,请说明理由.
【分析】(1)利用|An﹣1An|=3|AnAn+1|,及|A1A2|=9,结合等比数列的通项公式求得|AnAn+1|,结合等比数列的求和公式,可得|A1A2|+|A2A3|+…+|An﹣1An|,从而得出An的坐标;确定{|OBn|}是以3为首项,2为公差的等差数列,可求Bn的坐标;
(2)①连接AnBn+1,设四边形AnBnBn+1An+1的面积为Sn,则Sn=;
②对于存在性问题,可先假设存在,即假设存在不同的三项Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列,代入求出结果,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解:(1)|An﹣1An|=3|AnAn+1|,且|A1A2|=10﹣1=9,
∴|AnAn+3|=|A1A2|=9×=.
∴An的坐标(0,),
∴{|OBn|}是以3为首项,2为公差的等差数列
∴Bn的坐标为(2n+3,2n+1).
则Sn==?()n﹣5×(2n+3)+?4[﹣]?=+.
②由Sn,Sn+1,Sn+2(n∈N*)恰好成等差数列,可得2()=+++
∴18(n+1)=27n+3(n+2),∴n=1,
∴存在连续的三项S8,S2,S3恰好成等差数列.
同课章节目录
